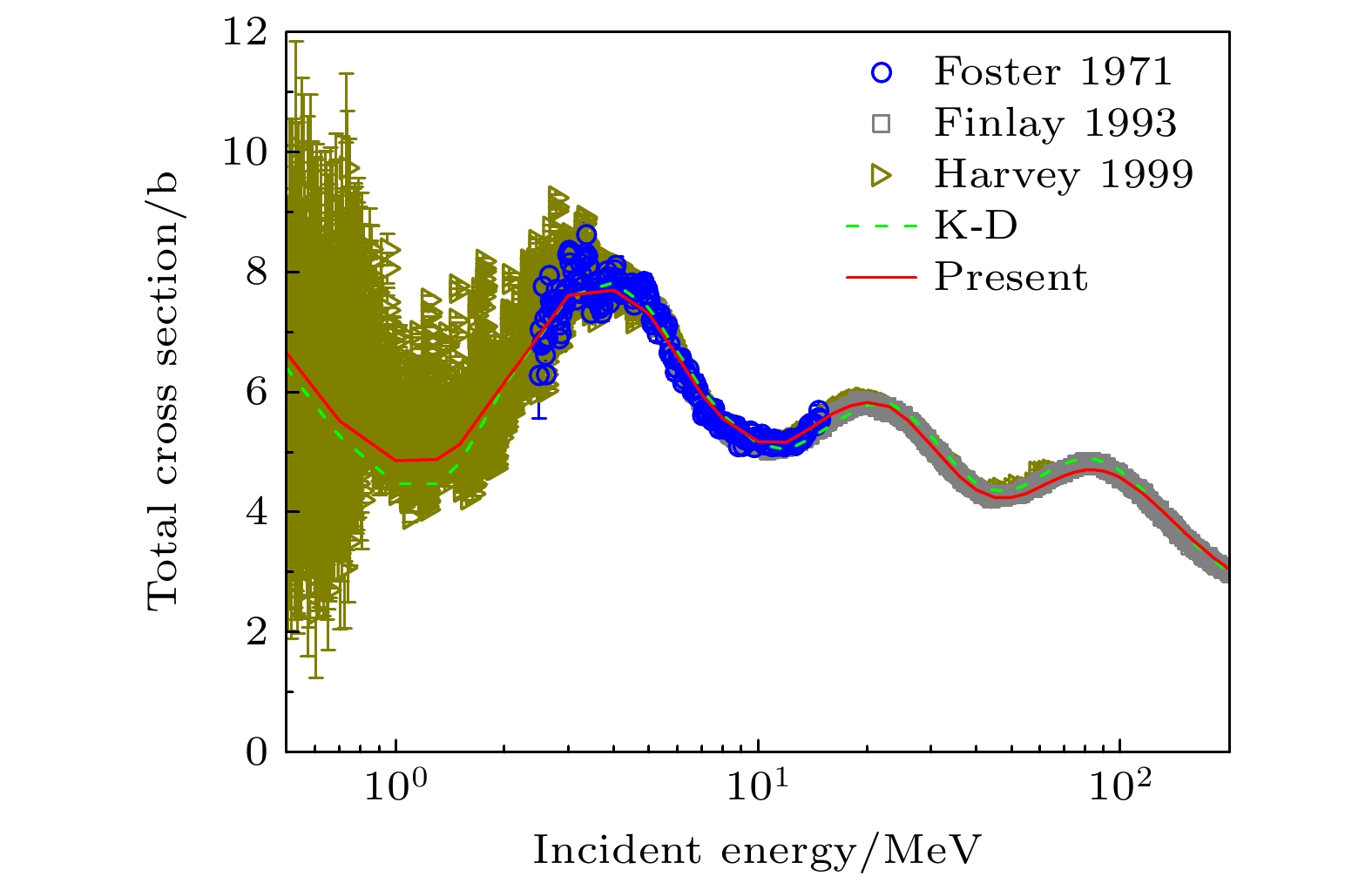
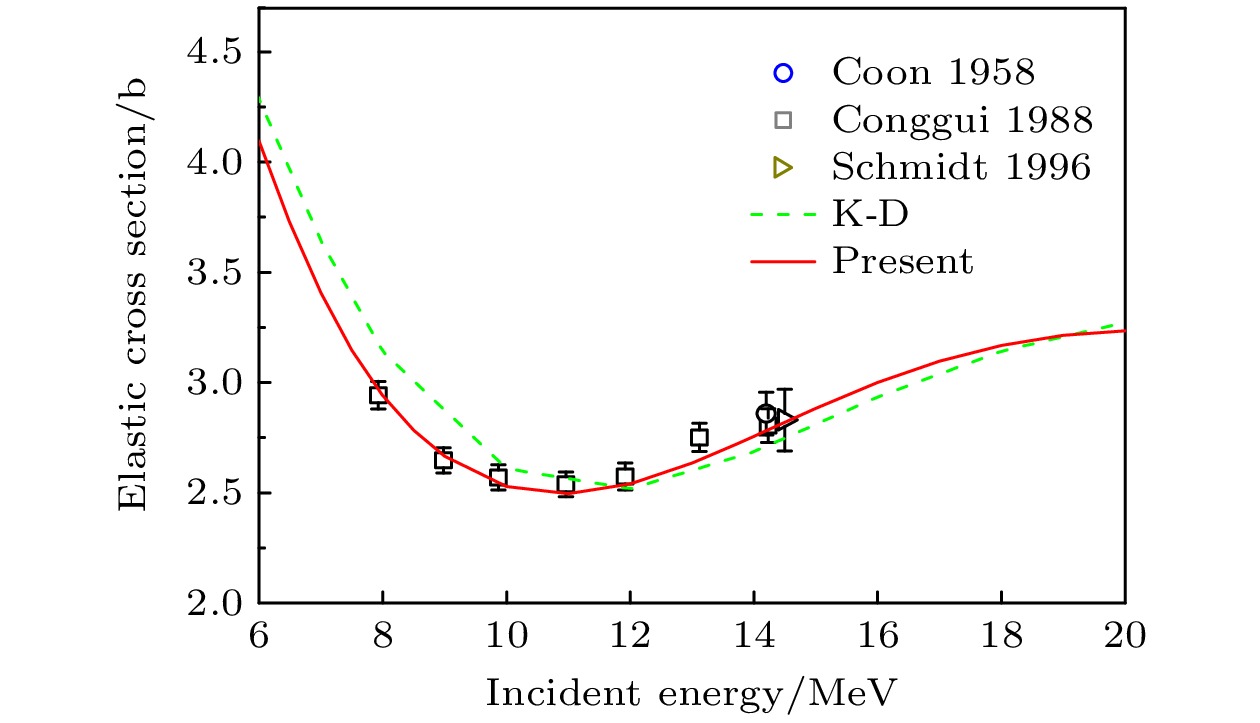
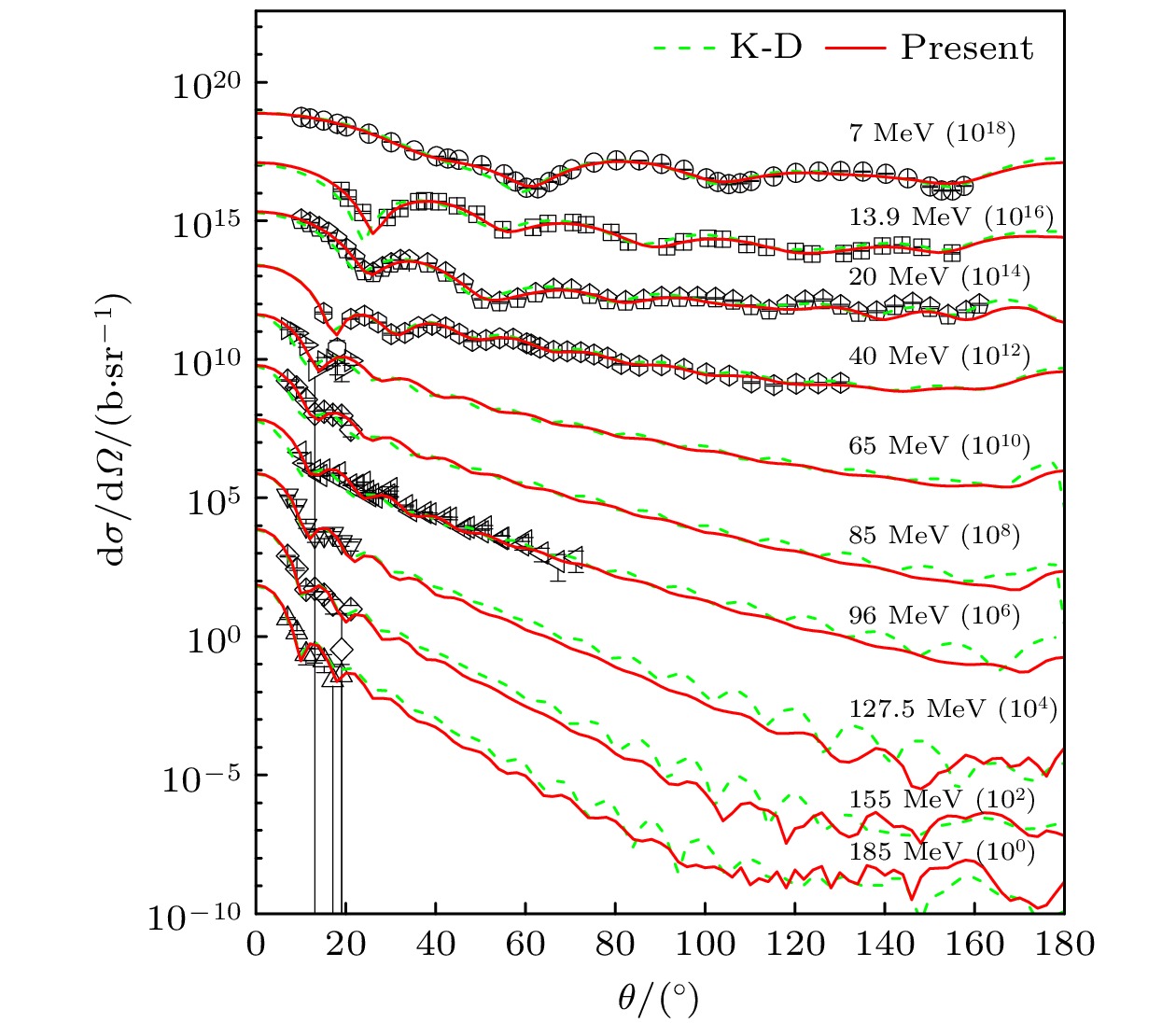
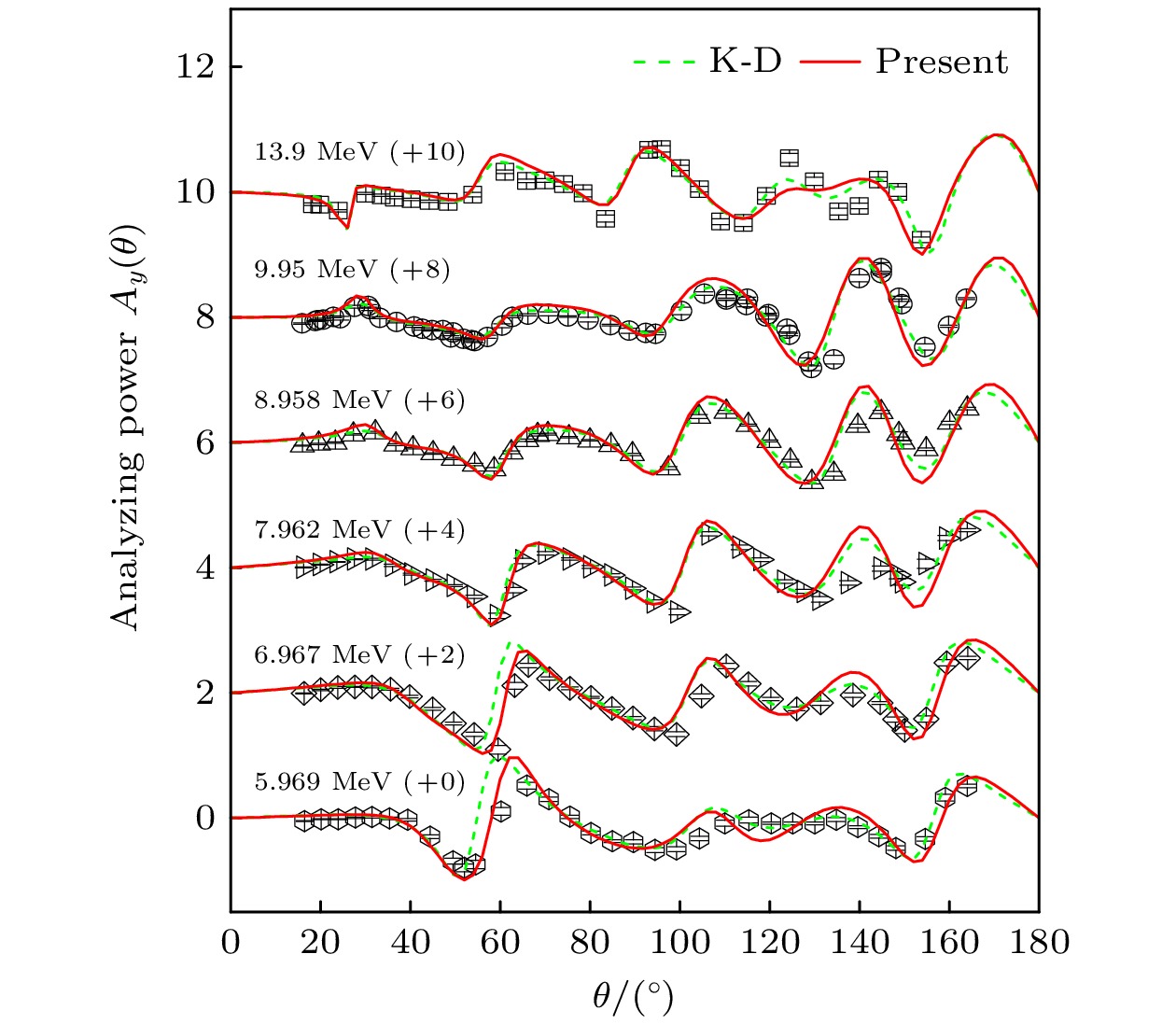
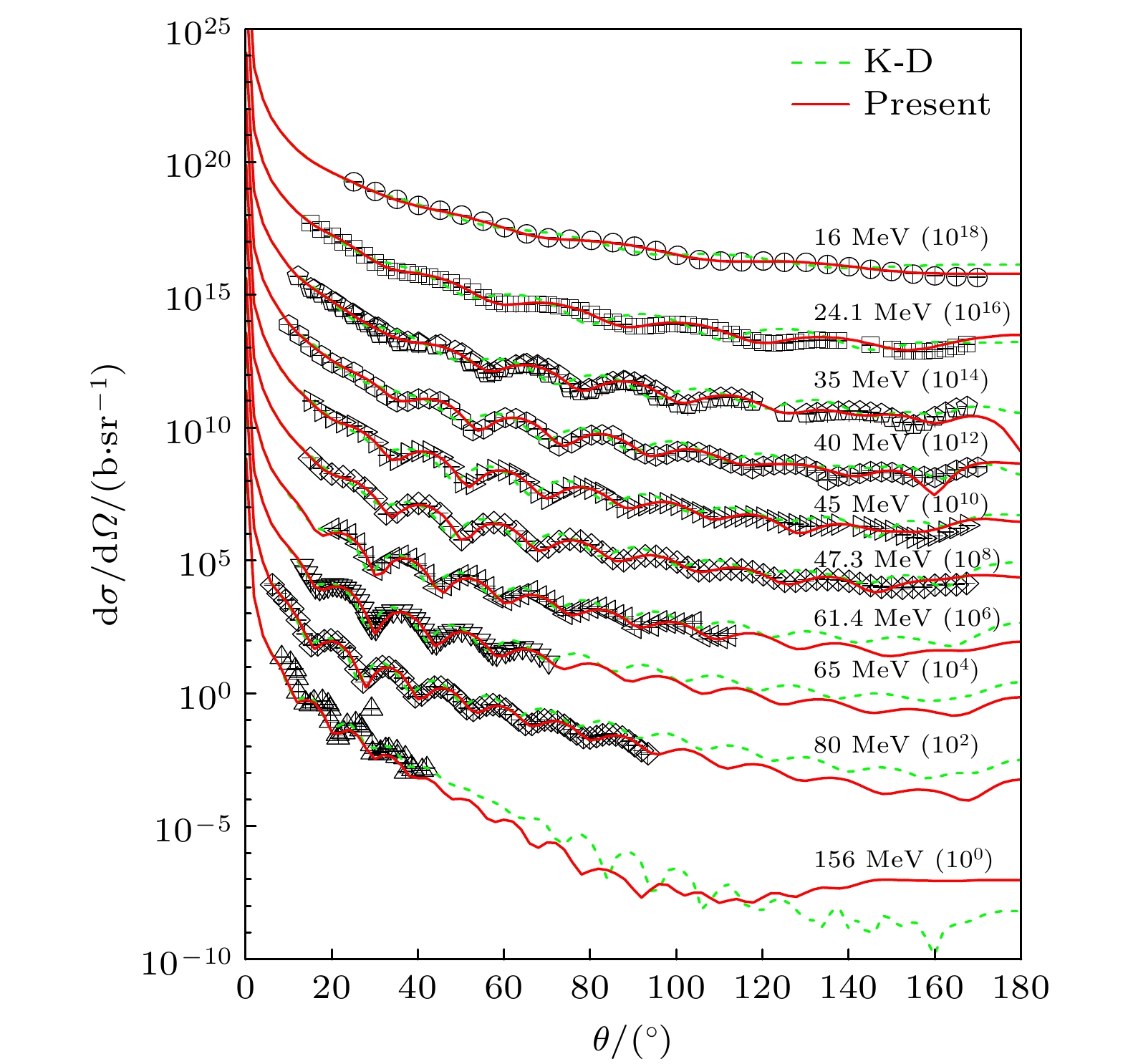
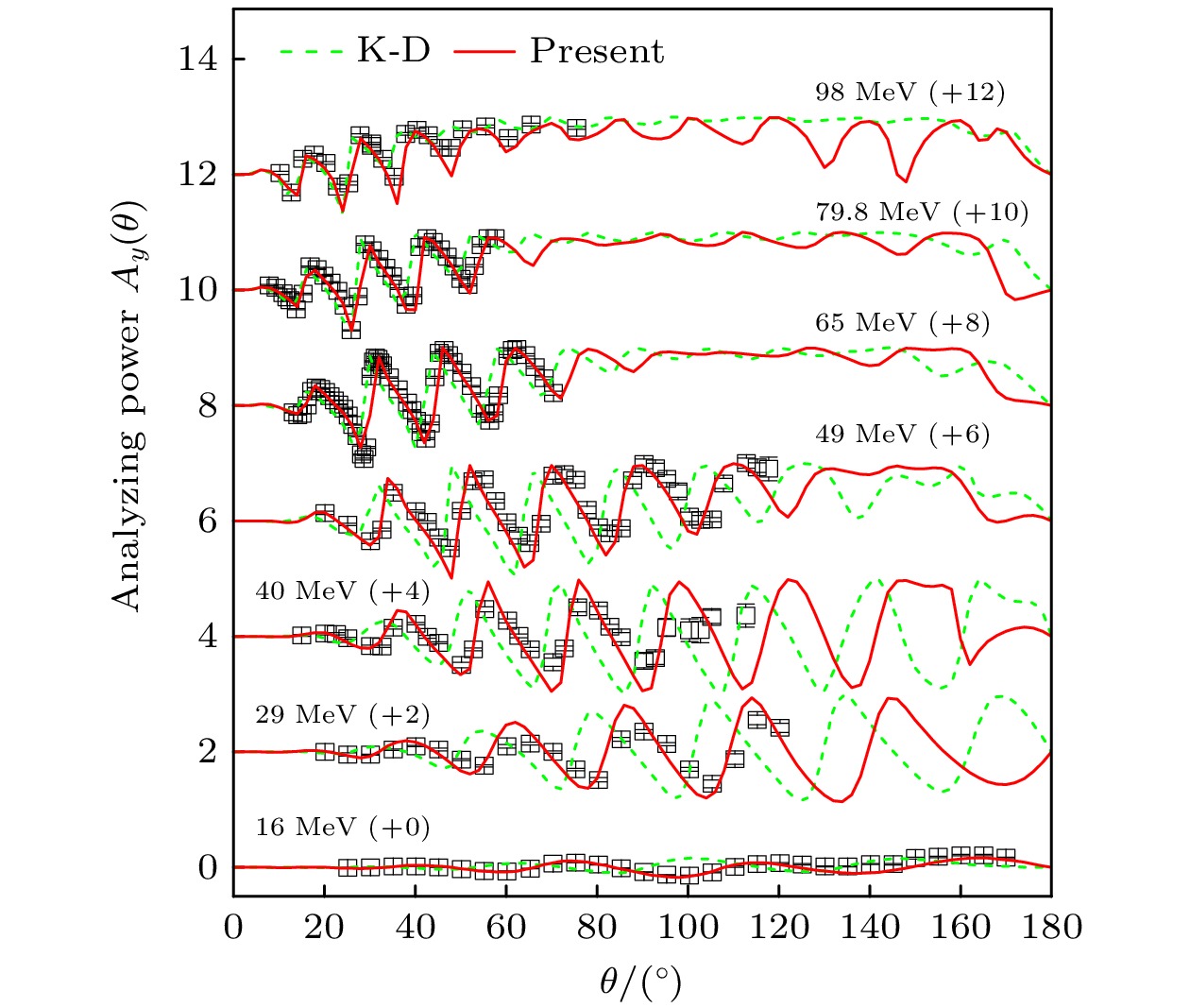
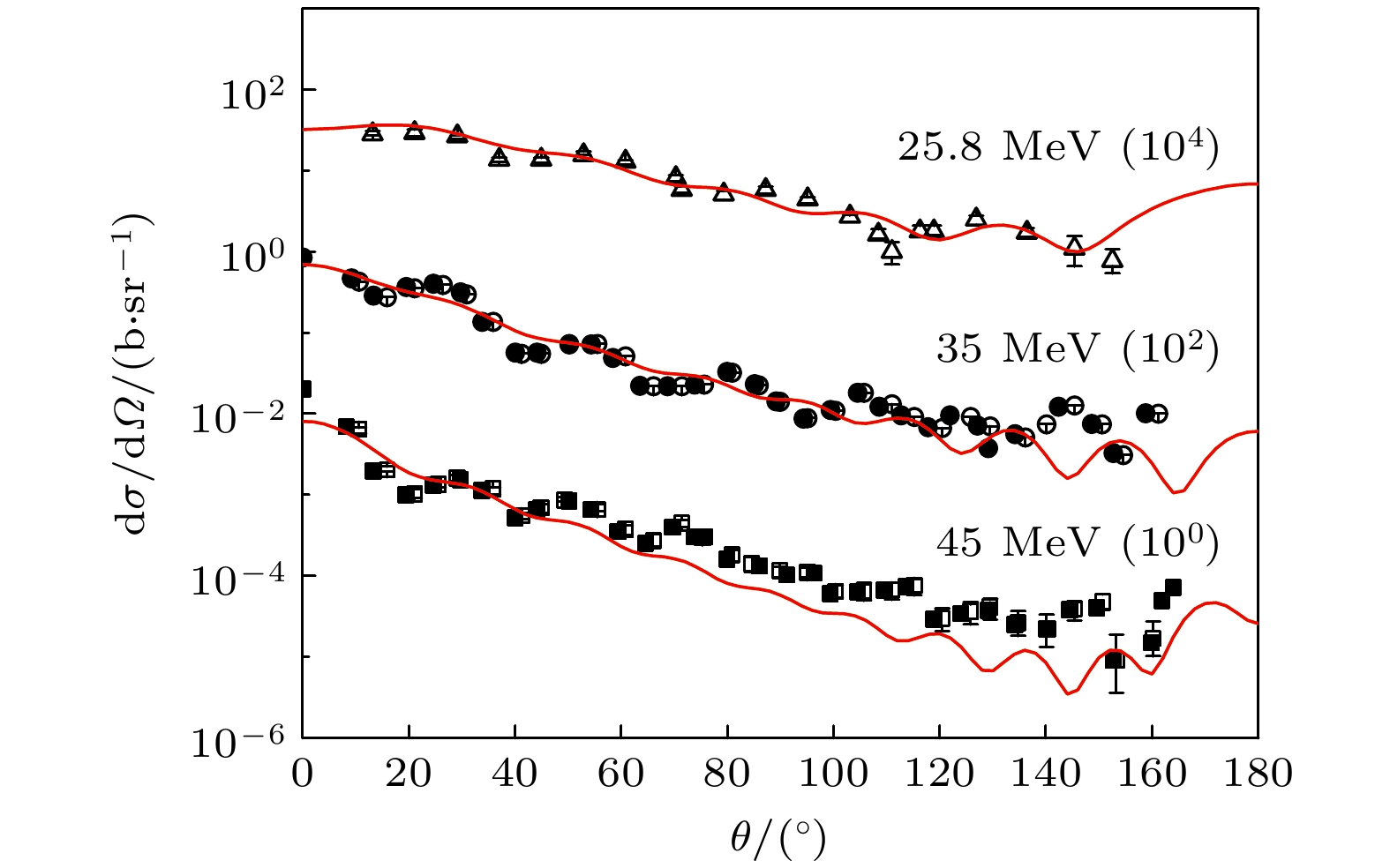
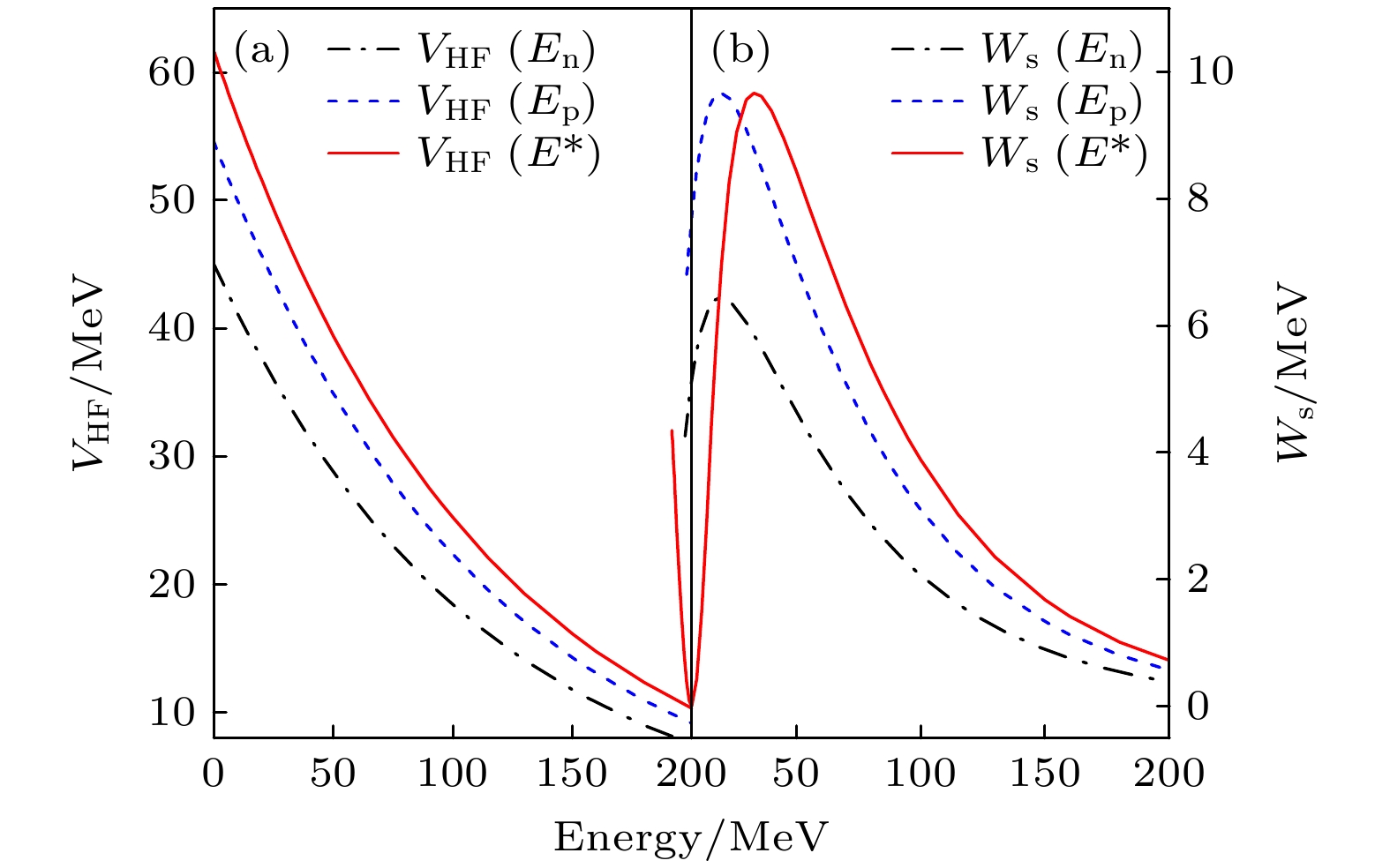
-
Lead is an important alloy material nuclide. And lead eutectic is also an important coolant, which is applied in the construction of Lead-cooled Fast Reactor such as The European Lead-cooled System (ELSY) and the China Lead-based Research reactor (CLEAR-I), as well as in research related to Generation-IV reactor. The study and calculation of lead nuclear data have important theoretical value and application prospects. 208Pb is the most stable and abundant isotope in lead nuclei, and high quality description of 208Pb nuclear scattering data is the key to achieving theoretical calculations of nuclear reaction data for lead nuclei. Based on the dispersive optical model, this work describes nucleon scattering on 208Pb by using the dispersive optical potential. The dispersive optical model potential is defined by energy-dependent real potentials, imaginary potentials, the corresponding dispersive contributions to the real potential which are calculated analytically from the corresponding imaginary potentials by using a dispersion relation, and isospin dependence is reasonably considered by introducing isovector component (i.e. Lane term) in the potential depth constants of the real Hartree-Fock potential $ V_{\rm{HF}}$ and the surface imaginary potential $ W_{\rm{s}}$. Unlike K-D potential, which requires two different sets of parameters to describe neutron and proton induced scattering data, this optical potential uses the same set of parameters to simultaneously describe nucleon-nucleus scattering data. The derived potential in this work shows a very good description of nucleon-nucleus scattering data on 208Pb up to 200 MeV. Calculated neutron total cross sections, neutron and proton elastic scattering angular distributions, as well as neutron and proton elastic analyzing powers are shown to be in good agreement with experimental data. Additionally, the difference in potential between the neutron and protons induced is described by the isovector term, a reasonable good prediction of quasielastic (p, n) scattering data is achieved.
-
图 1 中子和质子入射时的实部势$V_{\rm{HF}}$和表面虚部势$W_{\rm{s}}$深度随能量的变化情况
Fig. 1. Energy dependence of the real potential $V_{\rm{HF}}$ and the surface imaginary potential $W_{\rm{s}}$ depths for neutron and proton induced reactions on $^{208}{\rm{Pb}}$.
图 2 $^{208}{\rm{Pb}}$的中子总截面计算结果与K-D中子光学势给出的计算结果以及相关实验数据的比较
Fig. 2. Comparison of the calculated neutron total cross section for $^{208}{\rm{Pb}}$ with experimental data and those by K-D potential.
图 3 $^{208}{\rm{Pb}}$的中子弹性散射截面计算结果与K-D中子光学势给出的计算结果以及天然铅的相关实验数据的比较
Fig. 3. Comparison of the calculated neutron elastic cross section for $^{208}{\rm{Pb}}$ with experimental data and those by K-D potential.
图 4 $^{208}{\rm{Pb}}$的中子弹性散射角分布计算结果与K-D中子光学势给出的计算结果以及相关实验数据的比较
Fig. 4. Calculated neutron elastic scattering angular distributions for $^{208}{\rm{Pb}}$, compared with experimental data and those by K-D potential.
图 5 $^{208}{\rm{Pb}}$的中子弹性散射分析本领计算结果与K-D中子光学势给出的计算结果以及相关实验数据的比较
Fig. 5. Calculated neutron elastic scattering analyzing powers for $^{208}{\rm{Pb}}$, compared with experimental data and those by K-D potential.
图 6 $^{208}{\rm{Pb}}$的质子弹性散射角分布计算结果与K-D质子光学势给出的计算结果以及相关实验数据的比较
Fig. 6. Calculated proton elastic scattering angular distributions for $^{208}{\rm{Pb}}$, compared with experimental data and those by K-D potential.
图 7 $^{208}{\rm{Pb}}$的质子弹性散射分析本领计算结果与K-D质子光学势给出的计算结果以及相关实验数据的比较
Fig. 7. Calculated proton elastic scattering analyzing powers for $^{208}{\rm{Pb}}$, compared with experimental data and those by K-D potential.
图 8 $^{208}{\rm{Pb}}$的(p, n)准弹性散射角分布计算结果与相关实验数据的比较
Fig. 8. Comparison of (p, n) angular distributions of the quasielastic (p, n) scattering on $^{208}{\rm{Pb}}$ with experimental data.
表 1 $^{208}{\rm{Pb}}$的色散光学模型势参数
Table 1. Dispersive optical-model potential parameters for nucleon induced reactions on $^{208}{\rm{Pb}}$.
$V_{HF}$ Volume Surface Spin-orbit Coulomb Potential $V_{0}$ = 52.4 MeV $A_{\rm{v}}$ = 12.47 MeV $W_{0}$ = 15.82 MeV $V_{\rm{so}}$ = 8.1 MeV $C_{\rm{Coul}}$ = 1.0 MeV $\lambda_{\rm{HF}}$ = 0.009${\rm{MeV}}^{-1}$ $B_{\rm{v}}$ = 81.67 MeV $B_{\rm{s}}$ = 13.31 MeV $\lambda_{\rm{so}}$ = 0.005${\rm{MeV}}^{-1}$ $C_{\rm{viso}}$ = 23.85 MeV $E_{\rm{a}}$ = 56 MeV $C_{\rm{s}}$ = 0.02${\rm{MeV}}^{-1}$ $W_{\rm{SO}}$ = -3.1 MeV $C_{\rm{wiso}}$ = 14.98 MeV $B_{\rm{so}}$ = 160 MeV Geometry $r_{\rm{HF}}$ = 1.24${\rm{fm}}$ $r_{\rm{v}}$ = 1.25${\rm{fm}}$ $r_{\rm{s}}$ = 1.18${\rm{fm}}$ $r_{\rm{so}}$ = 1.08${\rm{fm}}$ $r_{\rm{c}}$ = 1.03${\rm{fm}}$ $a_{\rm{HF}}$ = 0.63${\rm{fm}}$ $a_{\rm{v}}$ = 0.69${\rm{fm}}$ $a_{\rm{s}}$ = 0.63${\rm{fm}}$ $a_{\rm{so}}$ = 0.59${\rm{fm}}$ $a_{\rm{c}}$ = 0.61${\rm{fm}}$ 
下载: 导出CSV
-
[1] 吴宜灿, 柏云清, 宋勇, 黄群英, 刘超, 王明煌, 周涛, 金鸣, 吴庆生, 汪建业, 蒋洁琼, 胡丽琴, 李春京, 高胜, 李亚洲, 龙鹏程, 赵柱民, 郁杰, FDS团队 2014 核科学与工程 34 201
Wu Y C, Bai Y Q, Song Y, Huang Q Y, Liu C, Wang M H, Zhou T, Jin M, Wu Q S, Wang J Y, Jang J Q, Hu L Q, Li C J, Gao S, Li Y Z, Long P C, Zhao Z M, Yu J, FDS Team 2014 Nucl. Sci. and Eng. 34 201
[2] Nifenecker H, David S, Loiseaux J M, Meplan O 2001 Nucl. Instrum. Methods A 463 505
Google Scholar
[3] Gudowski W 2000 Nucl. Phys. A 663-664 169c
Google Scholar
[4] Qaim S M 2001 Radiochim. Acta 89 189
Google Scholar
[5] Stankovskiy A, Malambu E, Eynde G V D, Diez C J 2014 Nucl. Data Sheets 118 513
Google Scholar
[6] Yang W S, Khalil H S 1999 Trans. Am. Nucl. Soc. 81 273
[7] Martin M J 2007 Nucl. Data Sheets 108 1583
Google Scholar
[8] Koning A J, Delaroche J P 2003 Nucl. Phys. A 713 231
Google Scholar
[9] Soukhovitski? E Sh, Capote R, Quesada J M, Chiba S 2005 Phys. Rev. C 72 024604
Google Scholar
[10] Capote R, Chiba S, Soukhovitski? E Sh, Quesada J M, Bauge E 2008 J. Nucl. Sci. Tech. 45 333
[11] Zhao X N, Sun W L, Soukhovitski? E Sh, Martyanov D S, Quesada J M, Capote R 2021 J. Phys. G: Nucl. Part. Phys. 48 075101
Google Scholar
[12] Zhao X N, Du W Q, Capote R, Soukhovitski? E Sh 2023 Phys. Rev. C 107 064606
Google Scholar
[13] Mahaux C, Sartor R 1986 Phys. Rev. Lett. 57 3015
Google Scholar
[14] 赵岫鸟, 杜文青 2023 72 222401
Google Scholar
Zhao X N, Du W Q 2023 Acta Phys. Sin. 72 222401
Google Scholar
[15] Quesada J M, Capote R, Soukhovitski? E Sh, Chiba S 2007 Phys. Rev. C 76 057602
Google Scholar
[16] Lipperheide R 1967 Z. Phys. 202 58
Google Scholar
[17] Mahaux C, Sartor R 1991 Nucl. Phys. A 528 253
Google Scholar
[18] Brown G E, Rho M 1981 Nucl. Phys. A 372 397
Google Scholar
[19] Delaroche J P, Wang Y, Rapaport J 1989 Phys. Rev. C 39 391
[20] Quesada J M, Capote R, Molina A, Lozano M, Raynal J 2003 Phys. Rev. C 67 067601
Google Scholar
[21] Chiba S, Iwamoto O, Yamanouti Y, Sugimoto M, Mizumoto M, Hasegawa K, Soukhovitski? E Sh, Porodzinski? Y V, Watanabe Y 1997 Nucl. Phys. A 624 305
Google Scholar
[22] Lane A M 1962 Phys. Rev. Lett. 8 171
Google Scholar
[23] Lane A M 1962 Nucl. Phys. 35 676
Google Scholar
[24] EXchange FORmat database (EXFOR) is maintained by the Network of Nuclear Reaction Data Centers (see www-nds.iaea.org/nrdc/). Data available online (e.g., at www-nds.iaea.org/exfor/
[25] Capote R, Herman M, Oblo $ \breve{z}$insk $ \acute{y}$ P, Young P G, Goriely S, Belgya T, Ignatyuk A V, Koning A J, Hilaire S, Plujko V A, Avrigeanu M, Bersillon O, Chadwick M B, Fukahori T, Ge Z G, Han Y L, Kailas S, Kopecky J, Maslov V M, Reffo G, Sin M, Soukhovitskiĩ E Sh, Talou P 2009 Nucl. Data Sheets 110 3107
下载:
计量
- 文章访问数: 310
- PDF下载量: 20
- 被引次数: 0
