-
零维系统模型已广泛应用于下一代托卡马克装置设计以及聚变反应堆等离子体性能的预测和分析, 但普遍采用物理近似和经验公式会导致较大的系统性误差. 本文通过引入等离子体平衡程序使主要等离子体分布参数及其计算基于磁面信息, 引入Sauter模型的自举电流系数与碰撞率变化关系改进自举电流计算, 利用EAST上的实验结果对改进后的模型进行验证, 零维系统模型计算结果与动理学平衡分析结果基本符合. 利用改进模型从已有实验结果出发, 对EAST上实现500 kA等离子体电流的稳态、长脉冲运行区所需要的加热/电流驱动功率及其能够达到的归一化比压进行了分析和预测. 计算结果表明, EAST在7.0—9.5 MW加热/驱动功率, 约束改善因子
$ {H}_{98} $ 为1.25—1.35, 归一化密度$ {f}_{{\rm{n}}{\rm{G}}} $ 约为0.9的参数范围内可以实现500 kA等离子体电流且自举电流份额在50%以上的稳态运行; 9.5 MW加热/驱动功率,$ {H}_{98} $ 为1.0—1.4,$ {f}_{{\rm{n}}{\rm{G}}} $ 为0.8—1.0的参数范围可以实现较高性能的长脉冲或稳态运行. 综合来说, 提升等离子体约束性能, 可在较低的加热/驱动功率下实现同样等离子体参数的完全非感应运行, 扩展等离子体运行区, 是实现高参数等离子体稳态运行最为有效的途径.The zero-dimensional system model has been widely used for predicting and analyzing plasma performance in fusion reactors and designing next-generation tokamaks. These models can quickly scan and calculate various parameter, and can be used for the design of device reference operation point and preparation for more accurate one-dimensional numerical simulations. They can also be used to predict device operational parameters and heating/ current drive conditions, providing a quick reference for experimental design. However, relying on physical approximations and empirical formulas can lead to significant systematic errors. In this work we introduce a plasma equilibrium program to obtain the main plasma profile parameters and their calculations based on magnetic surface information. The bootstrap current calculation is improved by introducing the relationship between the bootstrap current coefficient of the Sauter model and the collision rate change. The improved model is validated by using experimental results from EAST, and the results of the zero-dimensional system model calculations are found to be consistent with the results of kinetic equilibrium analysis. Based on the improved model and existing experimental results, the required heating/current drive power and achievable normalized beta for steady-state, long-pulse operation of the 500 kA plasma current on EAST are analyzed and predicted. The calculation results show that EAST can achieve steady-state operation at the 500 kA plasma current with bootstrap current fraction over 50% in the parameter range of 7.0–9.5 MW heating/driving power,$ {H}_{98} $ is 1.25–1.35, and$ {f}_{{\rm{n}}{\rm{G}}} $ ~0.9. Additionally, to maintain the total non-inductive current, the total heating/current drive power needs to be highly sensitive to plasma confinement and density, which is the most effective way to increase the bootstrap current fraction and reduce the peak heat loads on the divertor. Improving plasma confinement is the most effective way to achieve high bootstrap current fraction and reduce the peak heat load on the divertor. In this work, we also analyze the effect of heating power ratio on the bootstrap current, showing that adjusting the power ratio can change the bootstrap current fraction, and we further analyze the long-pulse operating region of EAST with a plasma current of 500 kA. In the range of 9.5 MW total heating/current driving power,$ {H}_{98} $ is 1.0–1.4, and normalized electron density$ {f}_{{\rm{n}}{\rm{G}}} $ is 0.8–1.0, high-performance long-pulse or fully non-inductive steady-state operation can be achieved, supporting the research on the physics of ITER and CFETR steady-state operation modes. In general, improving the plasma confinement performance can achieve fully non-inductive operation at lower heating/driving power while maintaining the same plasma parameters, and expand the plasma operating regime, which is the most effective way to achieve high-parameter steady-state operation of the plasma.-
Keywords:
- zero-dimensional system model /
- equilibrium solver /
- Sauter model /
- steady-state operation
[1] Chan V S, Stambaugh R D, Garofalo A M, Chu M S, Fisher R K, Greenfield C M, Humphreys D A, Lao L L, Leuer J A, Petrie T W, Prater R, Staebler G M, Snyder P B, St John H E, Turnbull A D, Wong C P C, Van Zeeland M A 2010 Fusion Sci. Technol. 57 66
Google Scholar
[2] Johner J 2011 Fusion Sci. Technol. 59 308
Google Scholar
[3] Kovari M, Kemp R, Lux H, Knight P, Morris J, Ward D J 2014 Fusion Eng. Des. 89 3054
Google Scholar
[4] Wan B N, Ding S Y, Qian J P, Li G Q, Xiao B J, Xu G S 2014 IEEE Trans. Plasma Sci. 42 495
Google Scholar
[5] Ding S Y, Wan B N, Wang L, Sun Y W, Lyu B 2016 IEEE Trans. Plasma Sci. 44 2502
Google Scholar
[6] Zohm H 2010 Fusion Sci. Technol. 58 613
Google Scholar
[7] Zohm H 2019 J. Fusion Energy 38 3
Google Scholar
[8] Stambaugh R D, Lao L L, Lazarus E A 1992 Nucl. Fusion 32 1642
Google Scholar
[9] Loarte A, Bosch S, Chankin A, Clement S, Herrmann A, Hill D, Itami K, Lingertat J, Lipschultz B, McCormick K, Monk R, Porter G D, Shimada M, Sugihara M 1999 J. Nucl. Mater. 266–269 587
[10] Liu-Lin Y R, Stambaugh R D 2004 Nucl. Fusion 44 548
Google Scholar
[11] Greenwald M, Terry J L, Wolfe S M, Ejima S, Bell M G, Kaye S M, Neilson G H 1988 Nucl. Fusion 28 2199
Google Scholar
[12] Liu-Lin Y R, Chan V, Prater R 2003 Phys. Plasmas 10 4064
Google Scholar
[13] Tonon G 1994 ISPP Workshop on Tokamak Concept Improvement Varenna, Italy, August 29–September 3, 1994 p31
[14] Fowler R, Holmes J, Rome J 1979 NFREYA: a Monte Carlo Beam Deposition Code for Noncircular Tokamak Plasmas Report
[15] ITER E 1999 Nucl. Fusion 39 2175
Google Scholar
[16] Yushmanov P N, Takizuka T, Riedel K S, Kardaun O J W F, Cordey J G, Kaye S M, Post D E 1990 Nucl. Fusion 30 1999
Google Scholar
[17] Dragojlovic Z, Raffray A R, Najmabadi F, Kessel C, Waganer L, El-Guebaly L, Bromberg L 2010 Fusion Eng. Des. 85 243
Google Scholar
[18] Grad H, Rubin H 1958 Proceedings of the Second United Nations International Conference on the Peaceful Uses of Atomic Energy (United Nations Geneva)
[19] Shafranov V 1958 Soviet Physics JETP 6 1013
[20] Sauter O, Angioni C, Liu-Lin Y R 1999 Phys. Plasmas 6 2834
Google Scholar
[21] Qian J, Wan B, Lao L L, Shen B, Sabbagh S A, Sun Y, Liu D, Xiao B, Ren Q, Gong X, Li J 2009 Plasma Sci. Technol. 11 142
Google Scholar
[22] Li G Q, Ren Q L, Qian J P, Lao L L, Ding S Y, Chen Y J, Liu Z X, Lu B, Zang Q 2013 Plasma Phys. Controlled Fusion 55 125008
Google Scholar
[23] 朱翔 2018 博士学位论文 (合肥: 中国科学技术大学)
Zhu X 2018 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[24] Stambaugh R D, Chan V S, Garofalo A M, Sawan M, Humphreys D A, Lao L L, Leuer J A, Petrie I W, Prater R, Snyder P B, Smith J P, Wong C P C 2011 Fusion Sci. Technol. 59 279
Google Scholar
[25] Sauter O, Angioni C, Lin-Liu Y R 2002 Phys. Plasmas 9 5140
Google Scholar
[26] 张家源 2022 博士学位论文 (合肥: 中国科学技术大学)
Zhang J Y 2022 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[27] Zhang J, Qian J, Gong X, Zhang B, Wu M, Li M, Zang Q, Zhu X, Lyu B, Liu H, Liang R, Jia T, Hu Y, Wang Z 2022 Fusion Eng. Des. 184 113283
Google Scholar
[28] Hender T C, Wesley J C, Bialek J, et al. 2007 Nucl. Fusion 47 S128
Google Scholar
[29] Wan B N, Liang Y, Gong X Z, et al. 2019 Nucl. Fusion 59 112003
Google Scholar
[30] Wan B N, Gong X Z, Liang Y, Xiang N, Xu G S, Sun Y, Wang L, Qian J P, Liu H Q, Zhang B, Xia T Y, Huang J, Ding R, Zhang T, Zuo G Z, Sun Z, Zeng L, Zhang X J, Zang Q, Lyu B, Garofalo A M, Li G Q, Li K D, Yang Q Q, for the E T, Collaborators 2022 Nucl. Fusion 62 042010
Google Scholar
[31] Gong X, Garofalo A M, Huang J, et al. 2019 Nucl. Fusion 59 086030
Google Scholar
[32] Zhuang G, Li G Q, Li J, Wan Y X, Liu Y, Wang X L, Song Y T, Chan V, Yang Q W, Wan B N, Duan X R, Fu P, Xiao B J, the C D T 2019 Nucl. Fusion 59 112010
Google Scholar
[33] Pitts R A, Bonnin X, Escourbiac F, Frerichs H, Gunn J P, Hirai T, Kukushkin A S, Kaveeva E, Miller M A, Moulton D, Rozhansky V, Senichenkov I, Sytova E, Schmitz O, Stangeby P C, De Temmerman G, Veselova I, Wiesen S 2019 Nucl. Mater. Energy 20 100696
Google Scholar
[34] Loarte A, Lipschultz B, Kukushkin A 2007 Nucl. Fusion 47 s203
Google Scholar
-
图 1 ONETWO动理学平衡分析[26] (红色线条)和零维系统模型(蓝色线条)分别对EAST炮号#90615在6540 ms时刻用Sauter模型计算的自举电流密度分布
Fig. 1. The ONETWO kinetic equilibrium analysis[26] (red line) and the zero-dimensional system model (blue line) respectively calculated the bootstrap current density profile of EAST shot #90615 at 6540 ms using the Sauter model.
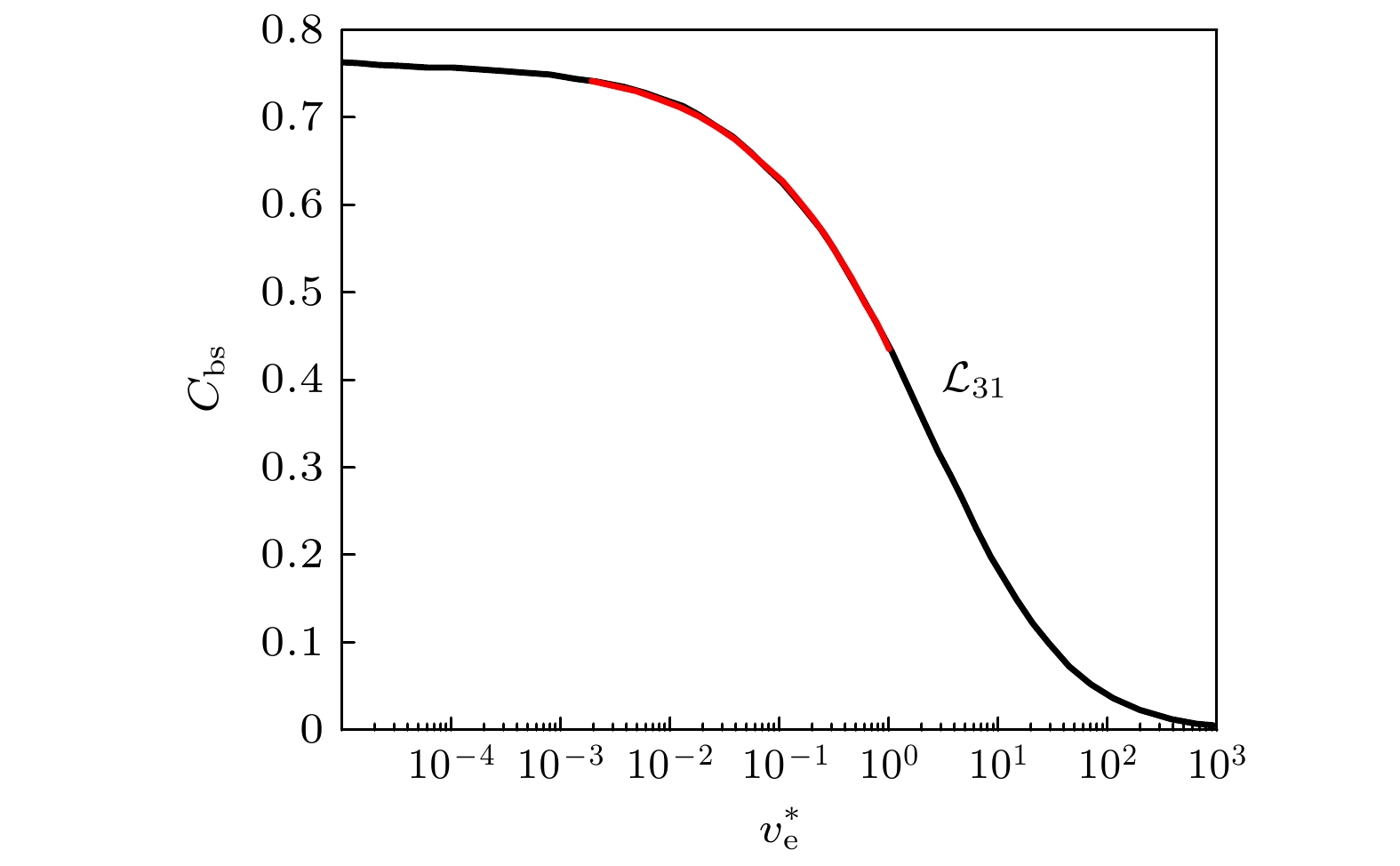
图 2 对Sauter模型
$ {\mathcal{L}}_{31} $ 部分与等离子体碰撞率的关系拟合, 黑线为$ {\mathcal{L}}_{31} $ (来自文献[20]), 红线为拟合曲线Fig. 2. Fitting the relationship between the Sauter model
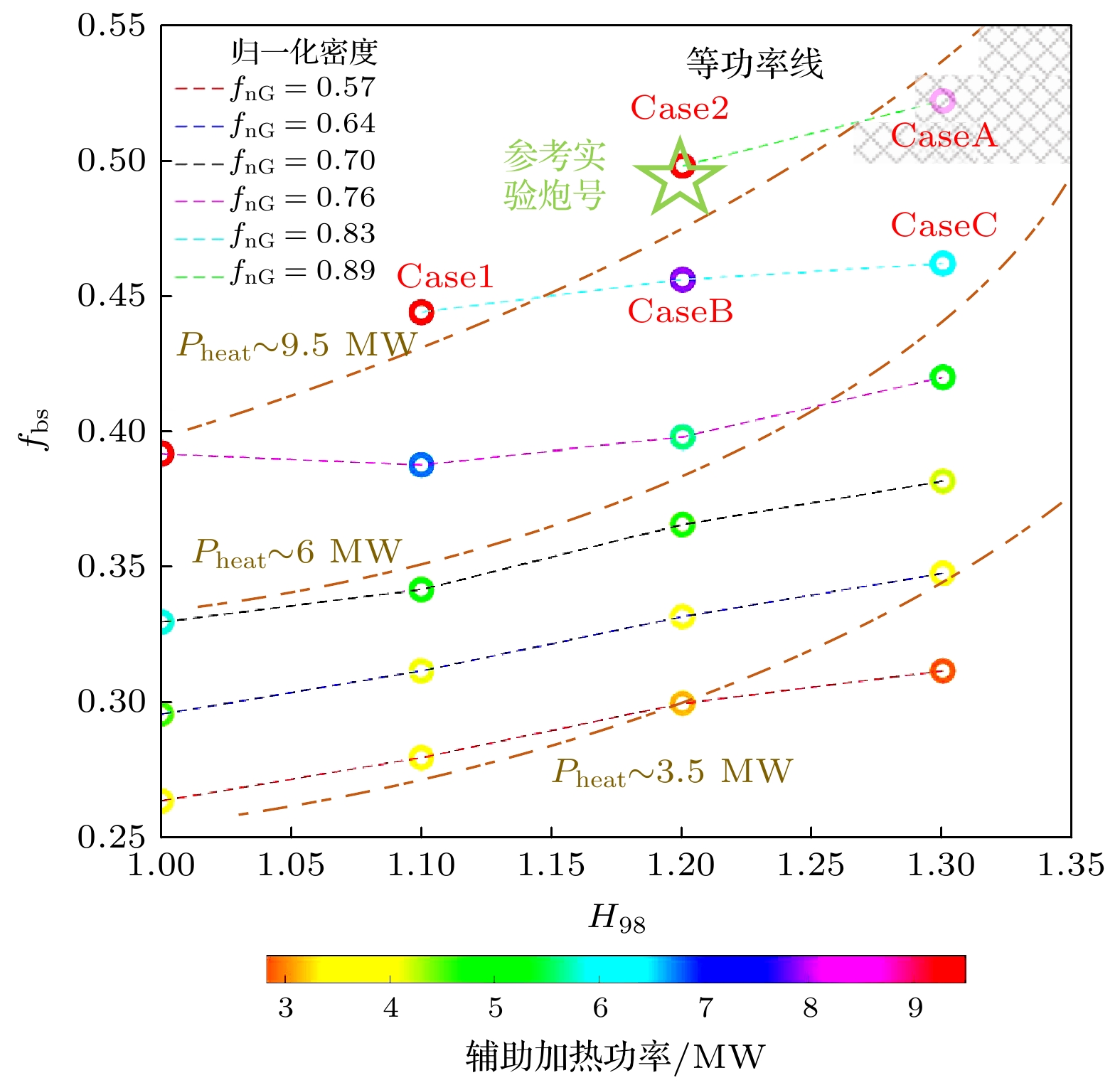
$ {\mathcal{L}}_{31} $ part and the collision rate of the plasma, the black line represents$ {\mathcal{L}}_{31} $ (from Ref[20]), and the red line represents the fitting curve.
图 3 EAST在500 kA等离子体电流在不同密度条件及不同能量约束改善因子下达到完全稳态运行所需要的辅助加热功率及所对应的自举电流份额
Fig. 3. The auxiliary heating power required for EAST to achieve steady-state operation under different plasma current densities and different improvement factors of energy confinement, as well as the corresponding fraction of bootstrap current for each condition.
图 5 EAST在500 kA等离子体电流9.5 MW加热功率下, 不同的电子密度与能量约束改善因子时的长脉冲运行能力
Fig. 5. EAST’s long-pulse operational capability under different electron densities and energy confinement improvement factors at 9.5 MW heating power and a plasma current of 500 kA.
表 1 零维系统模型计算所对应的实验条件
Table 1. Experimental conditions corresponding to the zero-dimensional system model calculation.
炮号 #89790 #90615 #101449 #94437 辅助加热
功率/MW离子回旋 0.21 0.28 0.53 0 电子回旋 0.63 0.63 0.98 0.63 低杂波 1.3 1.78 1.4 1.08 中性束 0 0 0 3.7 总功率/MW 2.14 2.69 2.91 5.41 电子弦密度/(1019 m–3) 3.8 4.7 4.1 4.5 归一化密度$ {f}_{{\rm{n}}{\rm{G}}} $ 0.65 0.81 0.60 0.73 等离子体电流/kA 369 370 363 366 
下载: 导出CSV
表 2 模型计算结果与磁平衡反演/动理学平衡分析结果对比
Table 2. Comparison between the model calculation results and the magnetic equilibrium inversion/kinetic equilibrium analysis results.
炮号 物理量 磁平衡反
演/动理学
平衡结果零维系统
模型计算误差% #89790 储能/kJ 175 164 6.3 $ {\beta }_{{\rm{N}}} $ 1.4 1.4 0.7 $ {\beta }_{{\rm{P}}} $ 1.64 1.60 2.4 $ {q}_{95} $ 6.5 6.15 5.4 $ {f}_{{\rm{b}}{\rm{s}}} $ 0.4 0.43 7.5 #90615 储能/kJ 195 186 4.6 $ {\beta }_{{\rm{N}}} $ 1.57 1.47 6.4 $ {\beta }_{{\rm{P}}} $ 1.8 1.88 4.4 $ {q}_{95} $ 6.4 6.9 7.8 $ {f}_{{\rm{b}}{\rm{s}}} $ 0.49 0.5 2.0 #101449 储能/kJ 231 218 5.6 $ {\beta }_{{\rm{N}}} $ 1.8 1.75 2.8 $ {\beta }_{{\rm{P}}} $ 2.62 2.34 10.7 $ {q}_{95} $ 8.23 7.4 10.1 $ {f}_{{\rm{b}}{\rm{s}}} $ 0.44 0.47 6.8 #94437 储能/kJ 243 228 6.2 $ {\beta }_{{\rm{N}}} $ 1.97 1.89 4.1 $ {\beta }_{{\rm{P}}} $ 2.31 2.31 0.3 $ {q}_{95} $ 6.92 7.2 4.0 $ {f}_{{\rm{b}}{\rm{s}}} $ 0.45 0.49 8.9
下载: 导出CSV
表 3 Case A完全非感应运行条件下不同的功率配比对应的自举电流份额
Table 3. The fraction of bootstrap current corresponding to different power ratios under fully non-inductive operation conditions for Case A.
离子回旋/MW 低杂波/MW 总加热/MW 自举电流份额 0 4.28 6.28 0.485 0.5 4.10 6.60 0.492 1.0 3.95 6.95 0.497 1.5 3.85 7.35 0.504 2.0 3.75 7.75 0.513 2.5 3.65 8.15 0.520 3.0 3.51 8.51 0.526 3.5 3.40 8.90 0.533 4.0 3.30 9.30 0.539
下载: 导出CSV
-
[1] Chan V S, Stambaugh R D, Garofalo A M, Chu M S, Fisher R K, Greenfield C M, Humphreys D A, Lao L L, Leuer J A, Petrie T W, Prater R, Staebler G M, Snyder P B, St John H E, Turnbull A D, Wong C P C, Van Zeeland M A 2010 Fusion Sci. Technol. 57 66
Google Scholar
[2] Johner J 2011 Fusion Sci. Technol. 59 308
Google Scholar
[3] Kovari M, Kemp R, Lux H, Knight P, Morris J, Ward D J 2014 Fusion Eng. Des. 89 3054
Google Scholar
[4] Wan B N, Ding S Y, Qian J P, Li G Q, Xiao B J, Xu G S 2014 IEEE Trans. Plasma Sci. 42 495
Google Scholar
[5] Ding S Y, Wan B N, Wang L, Sun Y W, Lyu B 2016 IEEE Trans. Plasma Sci. 44 2502
Google Scholar
[6] Zohm H 2010 Fusion Sci. Technol. 58 613
Google Scholar
[7] Zohm H 2019 J. Fusion Energy 38 3
Google Scholar
[8] Stambaugh R D, Lao L L, Lazarus E A 1992 Nucl. Fusion 32 1642
Google Scholar
[9] Loarte A, Bosch S, Chankin A, Clement S, Herrmann A, Hill D, Itami K, Lingertat J, Lipschultz B, McCormick K, Monk R, Porter G D, Shimada M, Sugihara M 1999 J. Nucl. Mater. 266–269 587
[10] Liu-Lin Y R, Stambaugh R D 2004 Nucl. Fusion 44 548
Google Scholar
[11] Greenwald M, Terry J L, Wolfe S M, Ejima S, Bell M G, Kaye S M, Neilson G H 1988 Nucl. Fusion 28 2199
Google Scholar
[12] Liu-Lin Y R, Chan V, Prater R 2003 Phys. Plasmas 10 4064
Google Scholar
[13] Tonon G 1994 ISPP Workshop on Tokamak Concept Improvement Varenna, Italy, August 29–September 3, 1994 p31
[14] Fowler R, Holmes J, Rome J 1979 NFREYA: a Monte Carlo Beam Deposition Code for Noncircular Tokamak Plasmas Report
[15] ITER E 1999 Nucl. Fusion 39 2175
Google Scholar
[16] Yushmanov P N, Takizuka T, Riedel K S, Kardaun O J W F, Cordey J G, Kaye S M, Post D E 1990 Nucl. Fusion 30 1999
Google Scholar
[17] Dragojlovic Z, Raffray A R, Najmabadi F, Kessel C, Waganer L, El-Guebaly L, Bromberg L 2010 Fusion Eng. Des. 85 243
Google Scholar
[18] Grad H, Rubin H 1958 Proceedings of the Second United Nations International Conference on the Peaceful Uses of Atomic Energy (United Nations Geneva)
[19] Shafranov V 1958 Soviet Physics JETP 6 1013
[20] Sauter O, Angioni C, Liu-Lin Y R 1999 Phys. Plasmas 6 2834
Google Scholar
[21] Qian J, Wan B, Lao L L, Shen B, Sabbagh S A, Sun Y, Liu D, Xiao B, Ren Q, Gong X, Li J 2009 Plasma Sci. Technol. 11 142
Google Scholar
[22] Li G Q, Ren Q L, Qian J P, Lao L L, Ding S Y, Chen Y J, Liu Z X, Lu B, Zang Q 2013 Plasma Phys. Controlled Fusion 55 125008
Google Scholar
[23] 朱翔 2018 博士学位论文 (合肥: 中国科学技术大学)
Zhu X 2018 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[24] Stambaugh R D, Chan V S, Garofalo A M, Sawan M, Humphreys D A, Lao L L, Leuer J A, Petrie I W, Prater R, Snyder P B, Smith J P, Wong C P C 2011 Fusion Sci. Technol. 59 279
Google Scholar
[25] Sauter O, Angioni C, Lin-Liu Y R 2002 Phys. Plasmas 9 5140
Google Scholar
[26] 张家源 2022 博士学位论文 (合肥: 中国科学技术大学)
Zhang J Y 2022 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[27] Zhang J, Qian J, Gong X, Zhang B, Wu M, Li M, Zang Q, Zhu X, Lyu B, Liu H, Liang R, Jia T, Hu Y, Wang Z 2022 Fusion Eng. Des. 184 113283
Google Scholar
[28] Hender T C, Wesley J C, Bialek J, et al. 2007 Nucl. Fusion 47 S128
Google Scholar
[29] Wan B N, Liang Y, Gong X Z, et al. 2019 Nucl. Fusion 59 112003
Google Scholar
[30] Wan B N, Gong X Z, Liang Y, Xiang N, Xu G S, Sun Y, Wang L, Qian J P, Liu H Q, Zhang B, Xia T Y, Huang J, Ding R, Zhang T, Zuo G Z, Sun Z, Zeng L, Zhang X J, Zang Q, Lyu B, Garofalo A M, Li G Q, Li K D, Yang Q Q, for the E T, Collaborators 2022 Nucl. Fusion 62 042010
Google Scholar
[31] Gong X, Garofalo A M, Huang J, et al. 2019 Nucl. Fusion 59 086030
Google Scholar
[32] Zhuang G, Li G Q, Li J, Wan Y X, Liu Y, Wang X L, Song Y T, Chan V, Yang Q W, Wan B N, Duan X R, Fu P, Xiao B J, the C D T 2019 Nucl. Fusion 59 112010
Google Scholar
[33] Pitts R A, Bonnin X, Escourbiac F, Frerichs H, Gunn J P, Hirai T, Kukushkin A S, Kaveeva E, Miller M A, Moulton D, Rozhansky V, Senichenkov I, Sytova E, Schmitz O, Stangeby P C, De Temmerman G, Veselova I, Wiesen S 2019 Nucl. Mater. Energy 20 100696
Google Scholar
[34] Loarte A, Lipschultz B, Kukushkin A 2007 Nucl. Fusion 47 s203
Google Scholar
下载:
计量
- 文章访问数: 2985
- PDF下载量: 52
- 被引次数: 0
