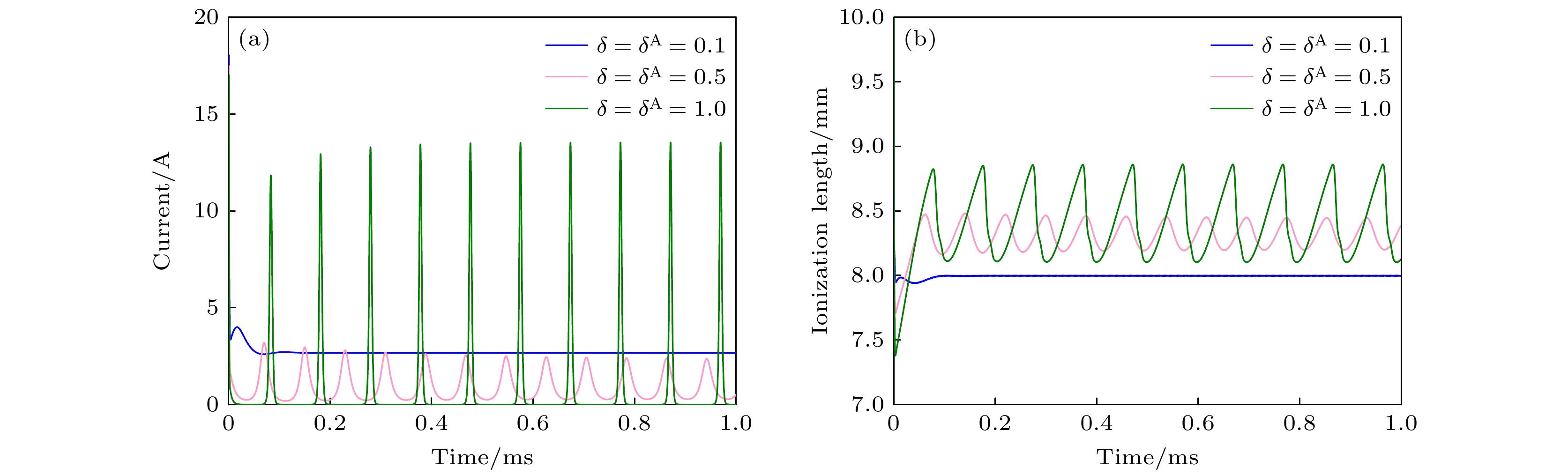
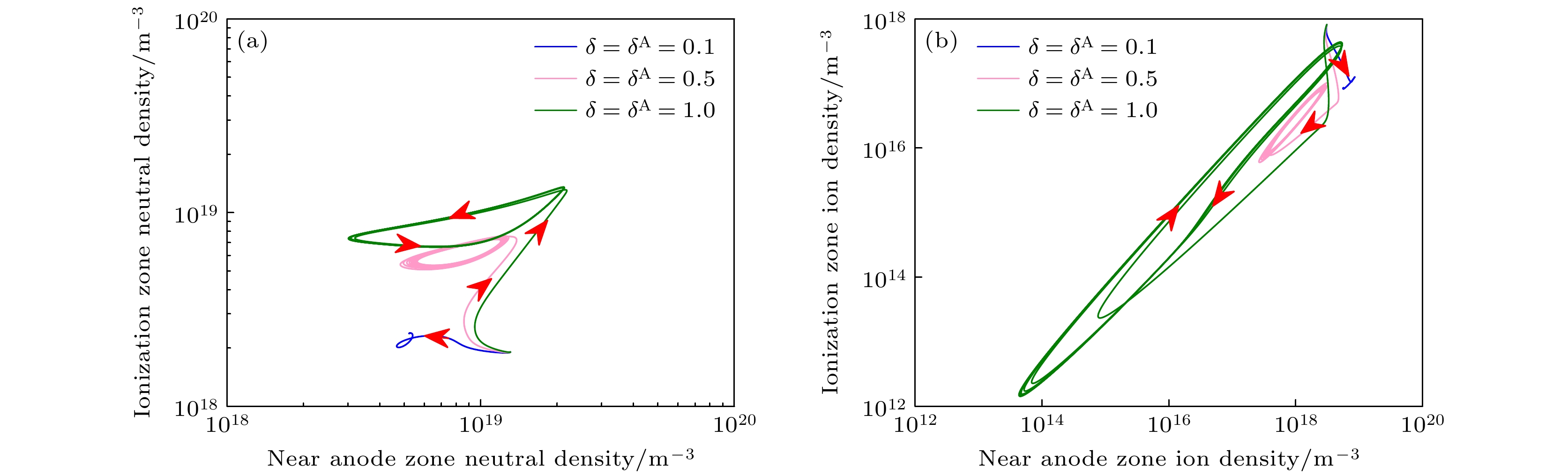
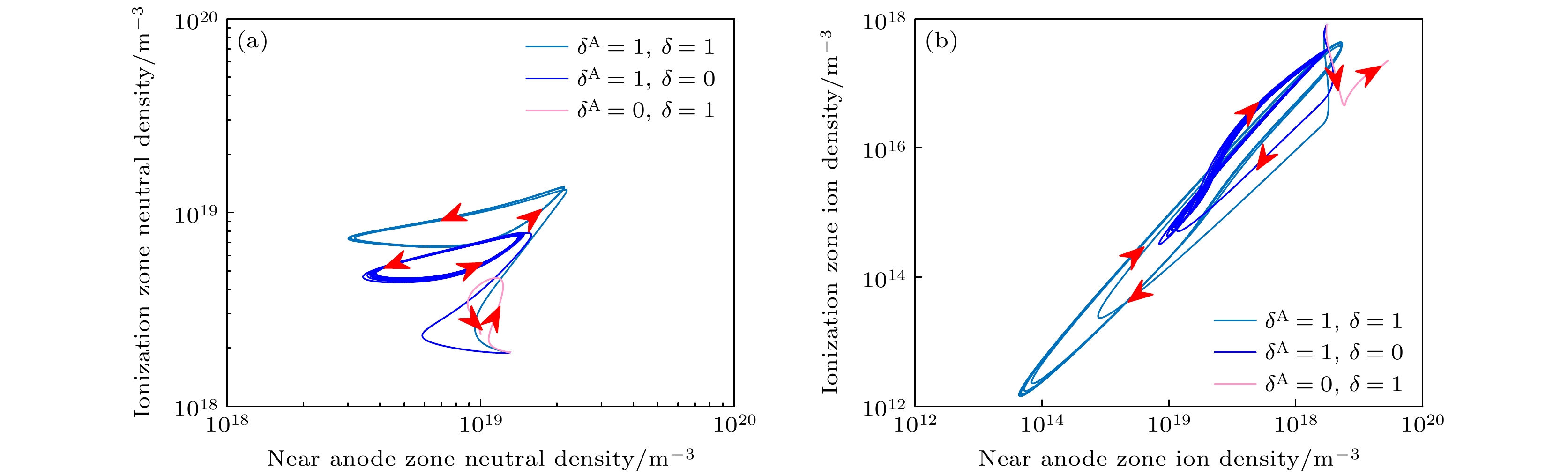
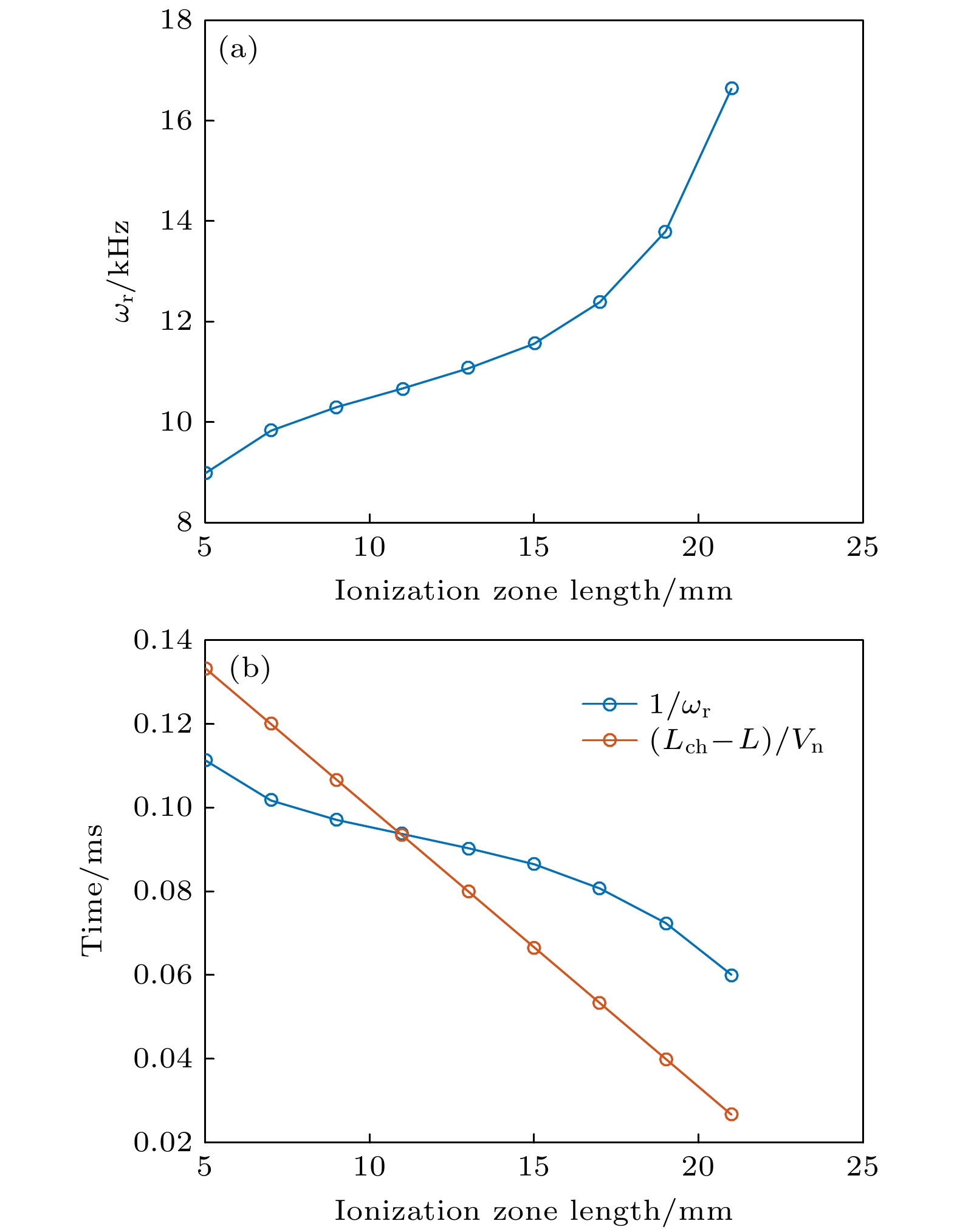
-
呼吸振荡作为霍尔推力器中的一种低频、大振幅放电不稳定性, 对推力器的性能及寿命有严重的影响. 本文利用包含了离子径向扩散和电子壁面相互作用的双区“捕食者-被捕食者”(Predator-Prey, P-P)模型, 对霍尔推力器中呼吸振荡的激发机理和影响因素开展了研究. 研究结果表明, 电子与壁面之间相互作用导致的能量耗散对呼吸振荡有抑制作用, 而近阳极区的离子径向扩散对呼吸振荡有激发作用. 依赖于近阳极区的离子径向扩散强度, 模式振荡频率以及放电电流的振荡峰值呈现非单调变化的趋势. 此外, 在推力器放电通道长度一定的情况下, 呼吸振荡的激发与电离区长度的变化无关, 而振荡的频率(周期)随着电离区长度的增大而增大(减小). 本文的研究结果将为霍尔推力器中呼吸振荡激发机理的认识以及呼吸振荡抑制新方法的提出提供理论支撑.Breathing oscillations as one of the low frequency, large amplitude discharge instabilities have serious influence on the performance and lifetime of Hall thrusters. In order to acquire a better understanding of the breathing-oscillation in the Hall thrusters and provide the effective suppression methods for breathing-oscillation, the excitation mechanism and influence factors of the breathing oscillations are investigated by utilizing the two-zone predator-prey (P-P) model in this paper. The two-zone P-P model divides the discharge channel of Hall thruster into two parts according to the working principle of Hall thruster: one is the near anode zone and the other e is the ionization zone. The model includes the ion radial diffusion effect and electrons-wall interaction effect. The four-order Range-Kuttle method is utilized to solve the nonlinear two-zone P-P model equation. The research results show that the interaction of electrons with the wall has the inhibition effect on the breathing oscillations caused by the energy consumption due to the colliding with discharge channel wall. However, ion radial diffusion effect which is near anode has an excitation effect on the breathing oscillation. The ion and neutral atom dynamic behaviors obviously show the P-P feature in the phase space. In other words, there is a phase difference between the change of ion density and the change of neutral particle density. Relying on the intensity of the ions radial diffusion effect, the mode oscillation frequency and oscillation amplitude of discharge current present non monotonic change trend. More specifically, with the increase of intensity of ion radial diffusion effect, the oscillation frequency first increases and then decreases. However, the discharge peak current first decreases and then increases. Furthermore, the breathing oscillations excitation is irrelevant to the length of ionization zone, and the oscillation frequency increases (oscillation period) with length of ionization zone increasing (decreasing), provided that the length of discharge channel is constant. The research results of this paper will provide support to make clear the excitation mechanism and propose the new method of suppressing the breathing oscillations in the hall thrusters.
-
Keywords:
- Hall thruster /
- breathing oscillations /
- two-zone predator-prey model /
- ions radial diffusion /
- electron-wall interaction
[1] Cusson S E, Dale E T, Jorns B A, Gallimore A D 2019 Phys. Plasmas 26 023506
Google Scholar
[2] Brown N P, Walker M L R 2020 Appl. Sci. 10 3775
Google Scholar
[3] Choueiri E Y 2001 Phys. Plasmas 8 1411
Google Scholar
[4] Kawashima R, Hara K, Komurasaki K 2018 Plasma Sources Sci. Technol. 27 035010
Google Scholar
[5] Chaplin V H, Jorns B A, Ortega A L, Mikellides I G, Conversano R W, Lobbia R B, Hofer R R 2018 J. Appl. Phys. 124 183302
Google Scholar
[6] Choueiri E Y, 2004 J. Propul. Power 20 193
Google Scholar
[7] Lopez O A, Mikellides I G, Sekerak M J, Jorns B A 2019 J. Appl. Phys. 125 033302
Google Scholar
[8] Wei L Q, Han K Wang C S, Li H, Zhang C H, Yu D R 2012 J. Vac. Sci. Technol. A 30 061304
Google Scholar
[9] Romadanov I, Raitses Y, Smolyakov A 2018 Plasma Sources Sci. Technol. 27 094006
Google Scholar
[10] Tilinin G N 1977 Soviet Tech. Phys. 206 2900
[11] Fife J M, Martinez-Sanchez M, Szabo J 1997 33rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Seattle, WA, July 6–9, 1997 p12
[12] Boeuf J P, Garrigues L 1998 J. Appl. Phys. 84 3541
Google Scholar
[13] Darnon F, Lyszyk M, Bouchoule A 1997 33rd AIAA/ASME/ SAE/ASEE Joint Propulsion Conference & Exhibit Seattle, WA, July 6–9, 1997 p6–9 AIAA–1997–3051
[14] Barral S, Makowski M, Peradzyński Z, Dudeck M 2005 Phys. Plasmas 12 073504
Google Scholar
[15] Chable S, Rogier F 2005 Phys. Plasmas 12 033504
Google Scholar
[16] Huang W S, Kamhawi H, Lobbia R B, Brown D 2014 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference Cleveland OH, July 28–30, 2014, AIAA–2014–3708
[17] Linnell J A, Gallimore A D 2006 Phys. Plasmas 13 093502
Google Scholar
[18] Xia G J, Ning Z X, Zhu X M, Wei L Q, Chen S W, Yu D R 2020 J. Propul. Power 36 1
Google Scholar
[19] Gascon N, Perot C, Bonhomme G, Caron X, Bechu S, Lasgorceix P, Izrar B, Dudeck M 1999 35th AIAA/ASME/SAE/ASEE Joint Propulsion Conference Los Angeles, CA, June 20–24, 1999, pAIAA–1999–2427
[20] Gascon N, Barral S, Dudeck M 2003 Phys. Plasmas 10 4123
Google Scholar
[21] Yamamoto N, Komurasaki K, Arakawa Y 2005 J. Propul. Power 21 870
Google Scholar
[22] Lobbia R B, Gallimore A D 2010 Rev. Sci. Instrum. 81 073503
Google Scholar
[23] Tahara H, Imanaka K, Yuge S 2006 Vacuum 80 1216
Google Scholar
[24] Raitses Y, Smirnov A, Fisch N J 2007 Appl. Phys. Lett. 90 221502
Google Scholar
[25] Granstedt E M, Raitses Y, Fisch N J 2008 J. Appl. Phys. 104 103302
Google Scholar
[26] Smirnov A, Raitses Y, Fisch N J 2008 IEEE Trans. Plasma Sci. 36 1998
Google Scholar
[27] Tamida T, Nakagawa T, Suga I, Osuga H, Ozaki T, Matsui K 2007 J. Appl. Phys. 102 043304
Google Scholar
[28] Barral S, Miedzik, Ahedo E 2008 44th AIAA/ASME/SAE/ ASEE Joint Propulsion Conference & Exhibit Hartford CT, July 21–23, 2008, pAIAA–2008–4632
[29] Raitses Y, Romadanov I, Simmonds Jacob, Smolyakov A, Kaganovich I 2019 AIAA Propulsion and energy Forum Indianapolis, IN, August 19–22, 2019, AIAA–2019–4078
[30] Yu D R, Wang C S, Wei L Q, Gao C, Yu G 2008 Phys. Plasmas 15 113503
Google Scholar
[31] Wei L Q, Ning Z X, Peng E, Yu D R 2010 J. Vac. Sci. Technol. 15 28
[32] Barral S, Miedzik J 2011 J. Appl. Phys. 109 013302
Google Scholar
[33] Wei L Q, Li W B, Ding Y J, Yu D R 2018 Plasma Sci. Technol. 20 075502
Google Scholar
[34] Yu D R, Wei L Q, Zhao Z Y, Han K, Yan G J 2008 Phys. Plasmas 15 043502
Google Scholar
[35] Dale E T, Jorns B A 2019 36th International Electric Propulsion Conference University of Vienna, Austria, September 15–20, 2019 pIEPC–2019–354
[36] Barral S, Ahedo E 2009 Phys. Rev. E 79 046401
Google Scholar
[37] Amici R 2019 Ph. D. Dissertation (Pisa: Università di Pisa)
[38] Hara K, Sekerak M J, Boyd I D, Gallimore A D 2014 Phys. Plasmas 21 122103
Google Scholar
[39] Fabris A L, Young C V, Cappelli M A 2015 J. Appl. Phys. 118 233301
Google Scholar
-
图 1 无电子与壁面相互作用时离子径向扩散效应的影响 (a)—(c)近阳极区的中性原子密度、离子密度、电子温度; (d)—(f)电离区的中性原子密度、离子密度、电子温度
Fig. 1. Effect of radial diffusion of ions without electron wall interaction: (a)–(c) Neutral atoms density, ion density, and electron temperature in the near anode zone; (d)–(f) neutral atom density, ion density, and electron temperature in the ionization zone.
图 2 无电子与壁面相互作用时放电电流(a)和电离区长度(b)
Fig. 2. Discharge current (a) and length of ionization zone (b) without electron-wall interaction.
图 3 电离率与中性原子密度(a)和离子密度(b)之间的关系
Fig. 3. Relationship of ionization rate with neutral atom density (a) and ion density (b).
图 4 振荡频率(a)和电流峰值(b)随离子径向扩散强度的变化
Fig. 4. The oscillation frequency (a) and peak current (b) varying with ion radial diffusion strength.
图 5 中性原子密度(a)和离子密度(b)在相空间中的动力学行为
Fig. 5. Phase space dynamics for neutral atom density (a) and ion density (b).
图 6 同一区域中性原子密度(a)和离子密度(b)在相空间中的动力学行为
Fig. 6. Phase space dynamics for neutral atom density (a) and ion density (b) at the same zone.
图 7 有电子与壁面相互作用时近阳极区(实线)和电离区(虚线)的中性原子密度、离子密度、以及电子温度
Fig. 7. Neutral atom density, ion density, and electron temperature in the near anode zone (solid line) and ionization zone (dashed line) with electron-wall interaction effect.
图 8 有电子与壁面相互作用时放电电流(a)和电离区长度(b)
Fig. 8. Discharge current (a) and length of ionization zone (b) with electron-wall interaction effect.
图 9 离子径向扩散对中性原子密度(a)和离子密度(b)在相空间中的动力学行为的影响
Fig. 9. Ions radial diffusion effect on phase space dynamics of neutral atom density (a) and ion density (b).
图 10 离子径向扩散对放电电流的影响
Fig. 10. Influence of radial diffusion of ions on the discharge current.
图 11 电离区长度对振荡频率的影响
Fig. 11. Influence of length of ionization zone on the oscillation frequency.
-
[1] Cusson S E, Dale E T, Jorns B A, Gallimore A D 2019 Phys. Plasmas 26 023506
Google Scholar
[2] Brown N P, Walker M L R 2020 Appl. Sci. 10 3775
Google Scholar
[3] Choueiri E Y 2001 Phys. Plasmas 8 1411
Google Scholar
[4] Kawashima R, Hara K, Komurasaki K 2018 Plasma Sources Sci. Technol. 27 035010
Google Scholar
[5] Chaplin V H, Jorns B A, Ortega A L, Mikellides I G, Conversano R W, Lobbia R B, Hofer R R 2018 J. Appl. Phys. 124 183302
Google Scholar
[6] Choueiri E Y, 2004 J. Propul. Power 20 193
Google Scholar
[7] Lopez O A, Mikellides I G, Sekerak M J, Jorns B A 2019 J. Appl. Phys. 125 033302
Google Scholar
[8] Wei L Q, Han K Wang C S, Li H, Zhang C H, Yu D R 2012 J. Vac. Sci. Technol. A 30 061304
Google Scholar
[9] Romadanov I, Raitses Y, Smolyakov A 2018 Plasma Sources Sci. Technol. 27 094006
Google Scholar
[10] Tilinin G N 1977 Soviet Tech. Phys. 206 2900
[11] Fife J M, Martinez-Sanchez M, Szabo J 1997 33rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Seattle, WA, July 6–9, 1997 p12
[12] Boeuf J P, Garrigues L 1998 J. Appl. Phys. 84 3541
Google Scholar
[13] Darnon F, Lyszyk M, Bouchoule A 1997 33rd AIAA/ASME/ SAE/ASEE Joint Propulsion Conference & Exhibit Seattle, WA, July 6–9, 1997 p6–9 AIAA–1997–3051
[14] Barral S, Makowski M, Peradzyński Z, Dudeck M 2005 Phys. Plasmas 12 073504
Google Scholar
[15] Chable S, Rogier F 2005 Phys. Plasmas 12 033504
Google Scholar
[16] Huang W S, Kamhawi H, Lobbia R B, Brown D 2014 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference Cleveland OH, July 28–30, 2014, AIAA–2014–3708
[17] Linnell J A, Gallimore A D 2006 Phys. Plasmas 13 093502
Google Scholar
[18] Xia G J, Ning Z X, Zhu X M, Wei L Q, Chen S W, Yu D R 2020 J. Propul. Power 36 1
Google Scholar
[19] Gascon N, Perot C, Bonhomme G, Caron X, Bechu S, Lasgorceix P, Izrar B, Dudeck M 1999 35th AIAA/ASME/SAE/ASEE Joint Propulsion Conference Los Angeles, CA, June 20–24, 1999, pAIAA–1999–2427
[20] Gascon N, Barral S, Dudeck M 2003 Phys. Plasmas 10 4123
Google Scholar
[21] Yamamoto N, Komurasaki K, Arakawa Y 2005 J. Propul. Power 21 870
Google Scholar
[22] Lobbia R B, Gallimore A D 2010 Rev. Sci. Instrum. 81 073503
Google Scholar
[23] Tahara H, Imanaka K, Yuge S 2006 Vacuum 80 1216
Google Scholar
[24] Raitses Y, Smirnov A, Fisch N J 2007 Appl. Phys. Lett. 90 221502
Google Scholar
[25] Granstedt E M, Raitses Y, Fisch N J 2008 J. Appl. Phys. 104 103302
Google Scholar
[26] Smirnov A, Raitses Y, Fisch N J 2008 IEEE Trans. Plasma Sci. 36 1998
Google Scholar
[27] Tamida T, Nakagawa T, Suga I, Osuga H, Ozaki T, Matsui K 2007 J. Appl. Phys. 102 043304
Google Scholar
[28] Barral S, Miedzik, Ahedo E 2008 44th AIAA/ASME/SAE/ ASEE Joint Propulsion Conference & Exhibit Hartford CT, July 21–23, 2008, pAIAA–2008–4632
[29] Raitses Y, Romadanov I, Simmonds Jacob, Smolyakov A, Kaganovich I 2019 AIAA Propulsion and energy Forum Indianapolis, IN, August 19–22, 2019, AIAA–2019–4078
[30] Yu D R, Wang C S, Wei L Q, Gao C, Yu G 2008 Phys. Plasmas 15 113503
Google Scholar
[31] Wei L Q, Ning Z X, Peng E, Yu D R 2010 J. Vac. Sci. Technol. 15 28
[32] Barral S, Miedzik J 2011 J. Appl. Phys. 109 013302
Google Scholar
[33] Wei L Q, Li W B, Ding Y J, Yu D R 2018 Plasma Sci. Technol. 20 075502
Google Scholar
[34] Yu D R, Wei L Q, Zhao Z Y, Han K, Yan G J 2008 Phys. Plasmas 15 043502
Google Scholar
[35] Dale E T, Jorns B A 2019 36th International Electric Propulsion Conference University of Vienna, Austria, September 15–20, 2019 pIEPC–2019–354
[36] Barral S, Ahedo E 2009 Phys. Rev. E 79 046401
Google Scholar
[37] Amici R 2019 Ph. D. Dissertation (Pisa: Università di Pisa)
[38] Hara K, Sekerak M J, Boyd I D, Gallimore A D 2014 Phys. Plasmas 21 122103
Google Scholar
[39] Fabris A L, Young C V, Cappelli M A 2015 J. Appl. Phys. 118 233301
Google Scholar
下载:
计量
- 文章访问数: 3194
- PDF下载量: 77
- 被引次数: 0
