-
硅烯是硅原子蜂窝状排列构成的二维材料, 由于其层内硅原子不在同一平面上而易受到电场等调控, 近年来成为理论和实验研究的一个热点. 借助于第一性原理计算方法, 详细研究了硅烯和二维铁电材料
${\rm{In}}_{2}{\rm{S}}_3$ 单层材料异质结的堆垛形式和电子结构. 计算结果表明, 硅烯和${\rm{In}}_{2}{\rm{S}}_3$ 可以形成稳定的异质结,${\rm{In}}_{2}{\rm{S}}_3$ 衬底的自发铁电极化对硅烯能带有显著调控作用. 铁电极化方向向上时, 自发极化电场和衬底的共同作用在狄拉克点打开能隙, K和K'点贝利曲率符号相反, 对应能谷霍尔效应态. 铁电极化方向向下时, 硅烯和${\rm{In}}_{2}{\rm{S}}_3$ 之间间距变小, 费米能级有能带穿过, 对应金属态. 研究结果对铁电调控硅烯二维异质结提供参考, 为硅烯异质结在信息存储领域的应用指明方向.Silicene is a kind of two-dimensional material composed of a honeycomb arrangement of silicon atoms. Compared with the structure of graphene, the buckled structure of silicene weakens the$\pi—\pi$ overlaps and turns the hybrid orbitals from$\rm sp^2$ to$\rm sp^3$ , which enhances the spin-orbit coupling strength but still preserves the Dirac cone near K or K'. Owing to its buckled structure, silicene is susceptible to external parameters like electric field and substrate, which draws lots of attention both experimentally and theoretically. Recent progress of ferroelectricity in two-dimensional (2D) van der Waals materials found that the spontaneous ferroelectric polarization can be preserved even above room temperature, which inspires us to investigate how to tune the electric properties of silicene through the spontaneous polarization field of 2D ferroelectric substrate.${\rm In_{2}}X_3$ (X = Se,S,Te) Family recently were found to have single ferroelectric monolayers with reversible spontaneous electric polarization in both out-of-plane and in-plane orientations, and the lattice mismatch between silicene and$\rm In_{2}S_3$ is negligible. Therefore, we investigate the stacking and electric properties of silicene and monolayer$\rm In_{2}S_3$ heterostructure by the first-principles calculations. The spontaneous polarization field of$\rm In_{2}S_3$ is calculated to be 1.26$\rm μC {\cdot} cm^{-2}$ , comparable to the experimental results of$\rm In_{2}Se_3$ . We compare the different stacking order between silicene and$\rm In_{2}S_3$ . The calculated results shown that the AB stacking is the ground state stacking order, and the reversal of the ferroelectric polarization could tune the band structure of heterostructure. When the polarization direction of$\rm In_{2}S_3$ is upward, the layer distance between silicene and$\rm In_{2}S_3$ is 3.93 Å, the polarization field and substrate interaction together break the AB sublattice symmetry and induce a 1.8 meV band gap near the Dirac point of K and K', while the Berry curvature around K and K' have opposite signs, corresponding to valley Hall effect. When the polarization is downward, the layer distance decreases to 3.62 Å and the band gap around K and K' both increase to 30.8 meV. At the same time a 0.04e charge transfer makes some bands move across the Fermi energy, corresponding to metal state. Our results pave the way for studying the ferroelectric tuning silicene heterostructures and their potential applications in information industry.-
Keywords:
- silicene /
- ferroelectricity /
- heterostructure /
- valley Hall effect
[1] Qiao Z, Tse W K, Jiang H, Yao Y, Niu Q 2011 Phys. Rev. Lett. 107 256801
[2] Liu C C, Feng W, Yao Y 2011 Phys. Rev. Lett. 107 076802
Google Scholar
[3] Zhao J, Liu H, Yu Z, Quhe R, Zhou S, Wang Y, Liu C C, Zhong H, Han N, Lu J, Yao Y, Wu K 2016 Prog. Mater. Sci. 83 24
[4] Oostinga J B, Heersche H B, Liu X, Morpurgo A F, Vandersypen L M K 2008 Nat. Mater. 7 151
Google Scholar
[5] Zhang Y, Tang T T, Girit C, Hao Z, Martin M C, Zettl A, Crommie M F, Shen Y R, Wang F 2009 Nature 459 820
Google Scholar
[6] Drummond N D, Zólyomi V, Fal'ko V I 2012 Phys. Rev. B 85 075423
Google Scholar
[7] Yu Z, Pan H, Yao, Y 2015 Phys. Rev. B 92 155419
Google Scholar
[8] Ezawa M 2012 Phys. Rev. Lett. 109 055502
Google Scholar
[9] Ezawa M 2013 Phys. Rev. Lett. 110 026603
Google Scholar
[10] Ezawa M 2012 New J. Phys. 14 033003
Google Scholar
[11] Tao L, Cinquanta E, Chiappe D, Grazianetti C, Fanciulli M, Dubey M, Molle A, Akinwande D 2015 Nat. Nanotechnol. 10 227
[12] Vali M, Dideban D, Moezi N 2016 J. Comput. Electron. 15 138
[13] 计青山, 郝鸿雁, 张存喜, 王瑞 2015 64 087302
Google Scholar
Ji Q S, Hao H Y, Zhang C X, Wang R 2015 Acta Phys. Sin. 64 087302
Google Scholar
[14] 侯海燕, 姚慧, 李志坚, 聂一行 2018 67 086801
Google Scholar
Hou H Y, Yao H, Li Z J, Nie Y X 2018 Acta Phys. Sin. 67 086801
Google Scholar
[15] Vogt P, De Padova P, Quaresima C, Avila J, Frantzeskakis E, Asensio M C, Resta A, Ealet B, Le Lay G 2012 Phys. Rev. Lett. 108 155501
Google Scholar
[16] Feng B, Ding Z, Meng S, Yao Y, He X, Cheng P, Chen L, Wu K 2012 Nano Lett. 12 3507
Google Scholar
[17] Chiappe D, Scalise E, Cinquanta E, Grazianetti C, van den Broek B, Fanciulli M, Houssa M, Molle A 2014 Adv. Mater. 26 2096
Google Scholar
[18] Li G, Zhang L, Xu W, Pan J, Song S, Zhang Y, Zhou H, Wang Y, Bao L, Zhang Y Y, Du S, Ouyang M, Pantelides S T, Gao H J 2018 Adv. Mater. 30 1804650
Google Scholar
[19] Novoselov K S, Mishchenko A, Carvalho A, Castro Neto A H 2016 Science 353 6298
[20] Liu Y, Zhang S, He J, Wang Z M, Liu Z 2019 Nano-Micro Lett. 11 13
Google Scholar
[21] Zheng Y, Ni G X, Toh C T, Tan C Y, Yao K, Özyilmaz B 2010 Phys. Rev. Lett. 105 166602
Google Scholar
[22] Ding J, Wen L W, Li H D, Zhang Y 2017 Phys. Lett. A 381 1749
Google Scholar
[23] Fei Z, Zhao W, Palomaki T A, Sun B, Miller M K, Zhao Z, Yan J, Xu X, Cobden D H 2018 Nature 560 336
Google Scholar
[24] Zhang J J, Zhu D, Yakobson B I 2021 Nano Lett. 21 785
Google Scholar
[25] 王慧, 徐萌, 郑仁奎 2020 69 017301
Google Scholar
Wang H, Xu M, Zheng R K 2020 Acta Phys. Sin. 69 017301
Google Scholar
[26] Ye Q, Shen Y, Duan C 2021 Chin. Phys. Lett. 38 087702
Google Scholar
[27] Chang K, Liu J, Lin H, Wang N, Zhao K, Zhang A, Jin F, Zhong Y, Hu X, Duan W, Zhang Q, Fu L, Xue Q K, Chen X, Ji S H 2016 Science 353 274
Google Scholar
[28] Liu F, You L, Seyler K L, Li X, Yu P, Lin J, Wang X, Zhou J, Wang H, He H, Pantelides S T, Zhou W, Sharma P, Xu X, Ajayan P M, Wang J, Liu Z 2016 Nat. Commun. 7 12357
Google Scholar
[29] Ding W, Zhu J, Wang Z, Gao Y, Xiao D, Gu Y, Zhang Z, Zhu W 2017 Nat. Commun. 8 14956
Google Scholar
[30] Ding J, Wen L W, Wang Z P, Zhang Y 2021 Mater. Today Commun. 27 102452
Google Scholar
[31] Ding J, Wen L W, Chai W W, Liu S C, Li R X, Li H D, Zhang Y 2021 Appl. Surf. Sci. 567 150871
Google Scholar
[32] 宋蕊, 王必利, 冯凯, 王黎, 梁丹丹 2022 71 037101
Google Scholar
Song R, Wang B L, Feng K, Wang L, Liang D D 2022 Acta Phys. Sin. 71 037101
Google Scholar
[33] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169
Google Scholar
[34] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[35] Grimme S, Antony J, Ehrlich S, Krieg H 2010 J. Chem. Phys. 132 154104
Google Scholar
[36] Ding J, Shao D F, Li M, Wen L W, Tsymbal E Y 2021 Phys. Rev. Lett. 126 057601
Google Scholar
[37] Wan S, Li Y, Li W, Mao X, Wang C, Chen C, Dong J, Nie A, Xiang J, Liu Z, Zhu W, Zeng H 2019 Adv. Funct. Mater. 29 1808606
Google Scholar
[38] Sivadas N, Okamoto S, Xu X, Fennie C J, Xiao D 2018 Nano Lett. 18 7658
Google Scholar
[39] Chen M X, Zhong Z, Weinert M 2016 Phys. Rev. B 94 075409
Google Scholar
[40] Xiao D, Yao W, Niu Q 2007 Phys. Rev. Lett. 99 236809
Google Scholar
[41] Pan H, Li Z, Liu C C, Zhu G, Qiao Z, Yao Y 2014 Phys. Rev. Lett. 112 106802
[42] Thouless D J, Kohmoto M, Nightingale M P, den Nijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[43] Yao Y, Kleinman L, MacDonald A H, Sinova J, Jungwirth T, Wang D S, Wang E, Niu Q 2004 Phys. Rev. Lett. 92 037204
Google Scholar
-
图 1 硅烯与
${\rm{In}}_{2}{\rm{S}}_3$ 异质结的结构图 (a), (b) AA堆垛的俯视图和侧视图; (c), (d) AB堆垛的俯视图和侧视图Fig. 1. The structure of Silicene/
${\rm{In}}_{2}{\rm{S}}_3$ heterostructure: (a), (b) the top and side view of AA stacking; (c), (d) the top and side view of AB stacking
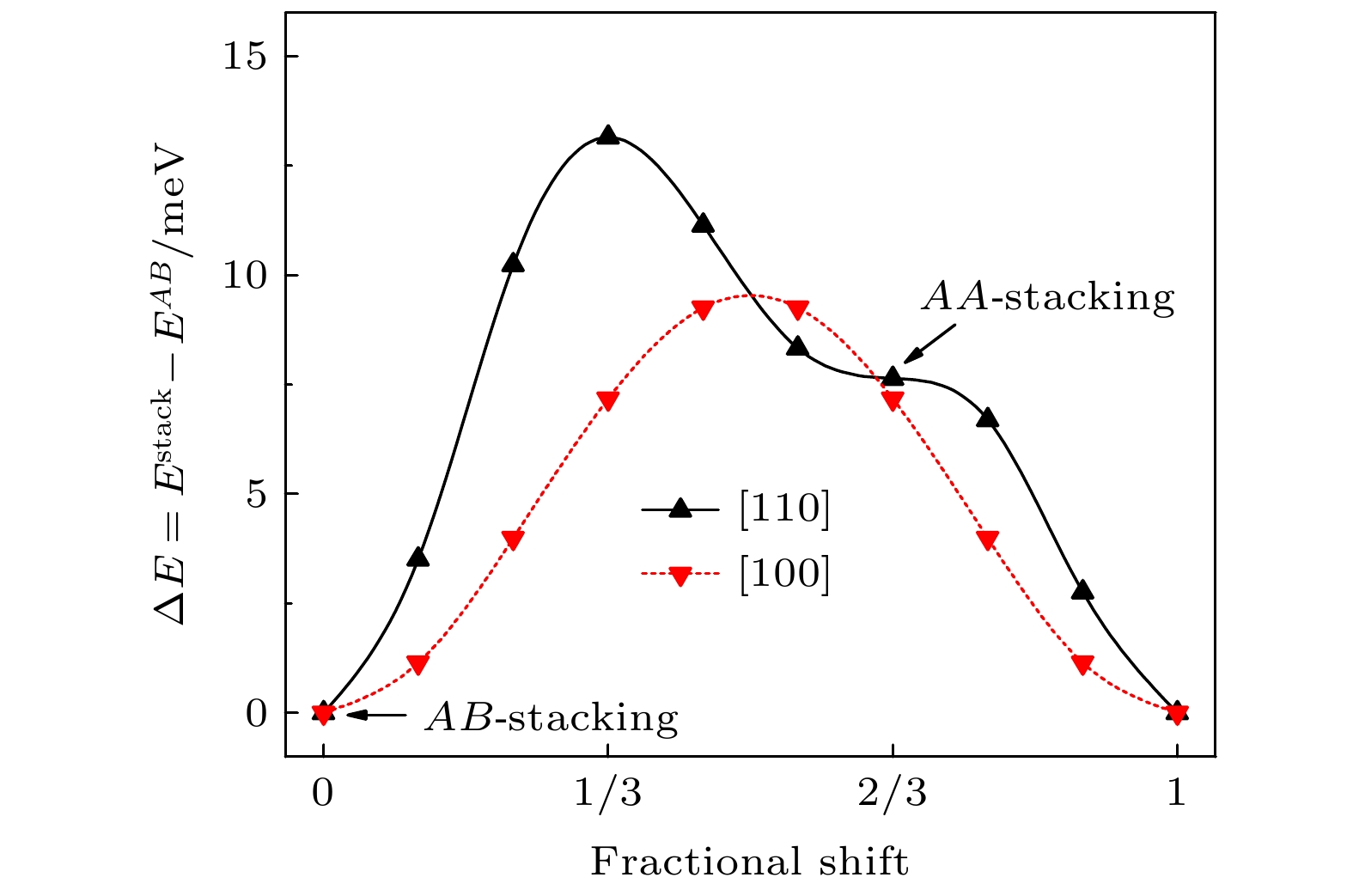
图 2 沿晶体表面不同方向横向平移时堆垛能变化情况. 图中给出沿[100](红色虚线)和[110](黑色实线)方向平移时堆垛能变化情况, AB堆垛在平面内平移[2/3, 2/3]即可得到AA堆垛
Fig. 2. Stacking energy as a function of lateral shift with respect AB stacking. The stacking energy are shown both for [100] (dotted red line) and [110] (solid black line) directions. AB stacking corresponding to a fractional lateral shift of [2/3, 2/3] of the top layer compared to AA stacking
图 3 硅烯/
${\rm{In}}_{2}{\rm{S}}_3$ 异质结能带图 (a)和(b)分别对应${\rm{In}}_{2}{\rm{S}}_3$ 极化方向向上和向下Fig. 3. Band structure of silicene/
${\rm{In}}_{2}{\rm{S}}_3$ heterostructure: (a) and (b) corresponding to the polarization of${\rm{In}}_{2}{\rm{S}}_3$ upward and downward, respectively
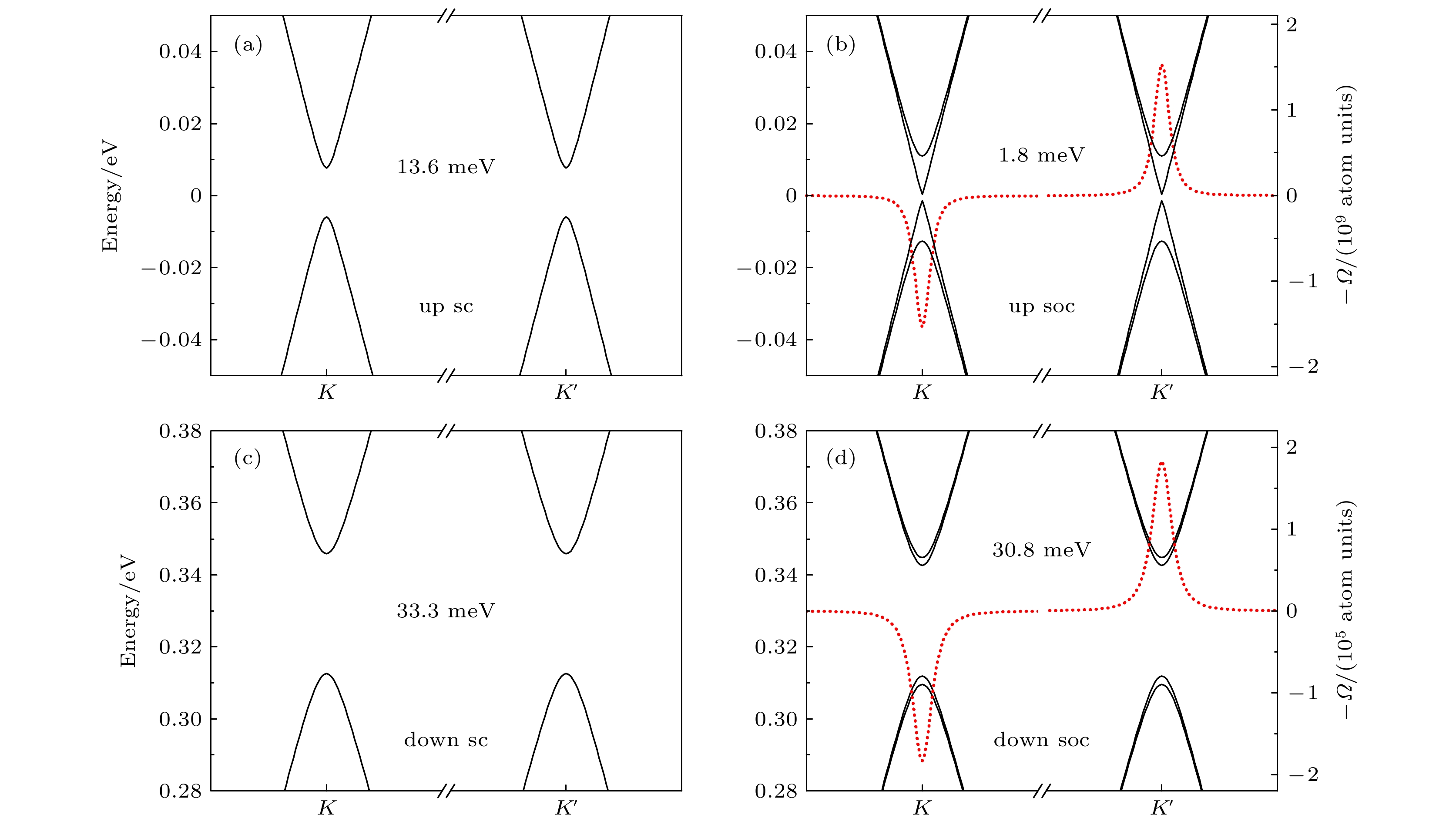
图 4 硅烯/
${\rm{In}}_{2}{\rm{S}}_3$ 异质结能带在K和K' 附近放大图 (a), (c)没有考虑自旋轨道耦合; (b), (d)考虑自旋轨道耦合, 红色虚线对应贝利曲率Fig. 4. Enlarged band structure of Silicene/
$\rm In_{2}S_3$ heterostructure around K and K': (a), (c) Calculations without spin orbit coupling; (b), (d) with spin orbit coupling, the red dotted line is the Berry curvature
图 5 硅烯/
${\rm{In}}_{2}{\rm{S}}_3$ 异质结垂直于界面方向局域势函数的平均值Fig. 5. Plane-averaged local potential of silicene/
${\rm{In}}_{2}{\rm{S}}_3$ heterostructure表 1
${\rm{In}}_{2}{\rm{S}}_3$ 极化方向改变时总能量, 结合能以及层间距和能隙变化情况. 能隙单位为meV, SOC指考虑自旋轨道耦合后数值Table 1. Total energy, adhesion energy, layer distance and energy gap with the polarization of
${\rm{In}}_{2}{\rm{S}}_3$ upward and downward. SOC refers to the energy gap (meV) calculated with spin-orbit coupling$E_{{\rm{tot}}}$/meV $E_{{\rm{ad}}}$/meV d/Å $E_{\rm{g}}$ (SOC) ${\rm{P} }_{ {\rm{In} }_2{\rm{S} }_3}$-up 22.87 12.51 3.93 13.6 (1.8) ${\rm{P} }_{ {\rm{In} }_2{\rm{S} }_3}$-down 0 37.16 3.62 33.3 (30.8) 
下载: 导出CSV
-
[1] Qiao Z, Tse W K, Jiang H, Yao Y, Niu Q 2011 Phys. Rev. Lett. 107 256801
[2] Liu C C, Feng W, Yao Y 2011 Phys. Rev. Lett. 107 076802
Google Scholar
[3] Zhao J, Liu H, Yu Z, Quhe R, Zhou S, Wang Y, Liu C C, Zhong H, Han N, Lu J, Yao Y, Wu K 2016 Prog. Mater. Sci. 83 24
[4] Oostinga J B, Heersche H B, Liu X, Morpurgo A F, Vandersypen L M K 2008 Nat. Mater. 7 151
Google Scholar
[5] Zhang Y, Tang T T, Girit C, Hao Z, Martin M C, Zettl A, Crommie M F, Shen Y R, Wang F 2009 Nature 459 820
Google Scholar
[6] Drummond N D, Zólyomi V, Fal'ko V I 2012 Phys. Rev. B 85 075423
Google Scholar
[7] Yu Z, Pan H, Yao, Y 2015 Phys. Rev. B 92 155419
Google Scholar
[8] Ezawa M 2012 Phys. Rev. Lett. 109 055502
Google Scholar
[9] Ezawa M 2013 Phys. Rev. Lett. 110 026603
Google Scholar
[10] Ezawa M 2012 New J. Phys. 14 033003
Google Scholar
[11] Tao L, Cinquanta E, Chiappe D, Grazianetti C, Fanciulli M, Dubey M, Molle A, Akinwande D 2015 Nat. Nanotechnol. 10 227
[12] Vali M, Dideban D, Moezi N 2016 J. Comput. Electron. 15 138
[13] 计青山, 郝鸿雁, 张存喜, 王瑞 2015 64 087302
Google Scholar
Ji Q S, Hao H Y, Zhang C X, Wang R 2015 Acta Phys. Sin. 64 087302
Google Scholar
[14] 侯海燕, 姚慧, 李志坚, 聂一行 2018 67 086801
Google Scholar
Hou H Y, Yao H, Li Z J, Nie Y X 2018 Acta Phys. Sin. 67 086801
Google Scholar
[15] Vogt P, De Padova P, Quaresima C, Avila J, Frantzeskakis E, Asensio M C, Resta A, Ealet B, Le Lay G 2012 Phys. Rev. Lett. 108 155501
Google Scholar
[16] Feng B, Ding Z, Meng S, Yao Y, He X, Cheng P, Chen L, Wu K 2012 Nano Lett. 12 3507
Google Scholar
[17] Chiappe D, Scalise E, Cinquanta E, Grazianetti C, van den Broek B, Fanciulli M, Houssa M, Molle A 2014 Adv. Mater. 26 2096
Google Scholar
[18] Li G, Zhang L, Xu W, Pan J, Song S, Zhang Y, Zhou H, Wang Y, Bao L, Zhang Y Y, Du S, Ouyang M, Pantelides S T, Gao H J 2018 Adv. Mater. 30 1804650
Google Scholar
[19] Novoselov K S, Mishchenko A, Carvalho A, Castro Neto A H 2016 Science 353 6298
[20] Liu Y, Zhang S, He J, Wang Z M, Liu Z 2019 Nano-Micro Lett. 11 13
Google Scholar
[21] Zheng Y, Ni G X, Toh C T, Tan C Y, Yao K, Özyilmaz B 2010 Phys. Rev. Lett. 105 166602
Google Scholar
[22] Ding J, Wen L W, Li H D, Zhang Y 2017 Phys. Lett. A 381 1749
Google Scholar
[23] Fei Z, Zhao W, Palomaki T A, Sun B, Miller M K, Zhao Z, Yan J, Xu X, Cobden D H 2018 Nature 560 336
Google Scholar
[24] Zhang J J, Zhu D, Yakobson B I 2021 Nano Lett. 21 785
Google Scholar
[25] 王慧, 徐萌, 郑仁奎 2020 69 017301
Google Scholar
Wang H, Xu M, Zheng R K 2020 Acta Phys. Sin. 69 017301
Google Scholar
[26] Ye Q, Shen Y, Duan C 2021 Chin. Phys. Lett. 38 087702
Google Scholar
[27] Chang K, Liu J, Lin H, Wang N, Zhao K, Zhang A, Jin F, Zhong Y, Hu X, Duan W, Zhang Q, Fu L, Xue Q K, Chen X, Ji S H 2016 Science 353 274
Google Scholar
[28] Liu F, You L, Seyler K L, Li X, Yu P, Lin J, Wang X, Zhou J, Wang H, He H, Pantelides S T, Zhou W, Sharma P, Xu X, Ajayan P M, Wang J, Liu Z 2016 Nat. Commun. 7 12357
Google Scholar
[29] Ding W, Zhu J, Wang Z, Gao Y, Xiao D, Gu Y, Zhang Z, Zhu W 2017 Nat. Commun. 8 14956
Google Scholar
[30] Ding J, Wen L W, Wang Z P, Zhang Y 2021 Mater. Today Commun. 27 102452
Google Scholar
[31] Ding J, Wen L W, Chai W W, Liu S C, Li R X, Li H D, Zhang Y 2021 Appl. Surf. Sci. 567 150871
Google Scholar
[32] 宋蕊, 王必利, 冯凯, 王黎, 梁丹丹 2022 71 037101
Google Scholar
Song R, Wang B L, Feng K, Wang L, Liang D D 2022 Acta Phys. Sin. 71 037101
Google Scholar
[33] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169
Google Scholar
[34] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[35] Grimme S, Antony J, Ehrlich S, Krieg H 2010 J. Chem. Phys. 132 154104
Google Scholar
[36] Ding J, Shao D F, Li M, Wen L W, Tsymbal E Y 2021 Phys. Rev. Lett. 126 057601
Google Scholar
[37] Wan S, Li Y, Li W, Mao X, Wang C, Chen C, Dong J, Nie A, Xiang J, Liu Z, Zhu W, Zeng H 2019 Adv. Funct. Mater. 29 1808606
Google Scholar
[38] Sivadas N, Okamoto S, Xu X, Fennie C J, Xiao D 2018 Nano Lett. 18 7658
Google Scholar
[39] Chen M X, Zhong Z, Weinert M 2016 Phys. Rev. B 94 075409
Google Scholar
[40] Xiao D, Yao W, Niu Q 2007 Phys. Rev. Lett. 99 236809
Google Scholar
[41] Pan H, Li Z, Liu C C, Zhu G, Qiao Z, Yao Y 2014 Phys. Rev. Lett. 112 106802
[42] Thouless D J, Kohmoto M, Nightingale M P, den Nijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[43] Yao Y, Kleinman L, MacDonald A H, Sinova J, Jungwirth T, Wang D S, Wang E, Niu Q 2004 Phys. Rev. Lett. 92 037204
Google Scholar
下载:
计量
- 文章访问数: 4074
- PDF下载量: 102
- 被引次数: 0
