-
基于力磁耦合效应的磁记忆检测技术, 被广泛应用于铁磁性结构件的应力和缺陷检测. 已有研究采用第一性原理针对α-Fe体系开展了轴向拉压作用下磁矩变化计算, 初步讨论了原子层面的磁检测技术力磁耦合机理. 本文以Fe-C和Fe-Mn掺杂体系为例, 在更为复杂的拉伸、压缩和剪切加载情形下, 深入讨论了α-Fe材料不同类型原子掺杂体系中磁矩变化等力磁耦合规律机理. 结果表明, α-Fe和掺杂体系在不同类型应变作用下磁矩和能量的变化规律存在不同. 结合态密度、能带结构和原子磁矩的详细分析, 发现掺杂元素通过影响Fe原子的磁矩, 使掺杂体系能带结构的形貌和态密度的峰值发生改变, 进而导致掺杂体系的磁矩和能量变化规律存在差异. 本研究从原子层面考虑了铁磁材料在不同荷载类型、不同掺杂元素和含量下的力磁耦合效应, 是磁记忆检测中多场耦合物理机理的重要补充.Magnetic non-destructive testing technology is widely used to detect stresses and defects in ferromagnetic materials based on the magneto-mechanical coupling effect. In the existing studies, calculated are the magnetic moment variations of the α-Fe system under axial tension and compression by using first-principles study, and the magneto-mechanical coupling mechanism is preliminarily discussed at an atomic level for the magnetic testing technology. In this work, taking the more complex doping systems Fe-C and Fe-Mn for examples, under different loading conditions of tension, compression and shearing, the coupling mechanisms such as the magnetic moment changes in different types of atomic doping systems are discussed in detail. The results show that the α-Fe and doping systems follow different changing laws of magnetic moments and energy under different types of strains. The detailed analyses of the density of states, the band structure, and the atomic magnetic moment show that doping elements change the morphology of band structure and the peak value of density of states by affecting the magnetic moment of Fe atoms, which leads the changing laws of magnetic moment and energy to be different from each other. In this work, discussed are the magneto-mechanical effects on the atomic level for ferromagnetic materials with different loading types, different doping elements and different element content. The results can be used as an important part of the multi-field coupling mechanism for magnetic testing technology.
-
Keywords:
- metal magnetic memory /
- testing mechanism /
- α-Fe doping systems /
- strain effect /
- magnetic moment
[1] De Sousa J M, Aguiar A L, Girão E C, Fonseca A F, Souza Filho A G, Galvão D S 2021 Chem. Phys 542 111052
Google Scholar
[2] 李君, 刘立胜, 徐爽, 张金咏 2020 69 043102
Google Scholar
Li J, Liu L S, Xu S, Zhang J Y 2020 Acta Phys. Sin. 69 043102
Google Scholar
[3] Hadji S, Bouhemadou A, Haddadi K, Cherrad D, Khenata R, Bin-Omran S, Al-Douri Y 2020 Physica B 589 412213
Google Scholar
[4] Kohn W, Sham L J 1965 Phys. Rev 140 A1133
Google Scholar
[5] Han Z K, Sarker D, Ouyang R, Mazheika A, Gao Y, Levchenko S V 2021 Nat. Commun 12 1833
Google Scholar
[6] 祝平, 张强, 芶华松, 王平平, 邵溥真, 小林郁夫, 武高辉 2021 70 178101
Google Scholar
Zhu P, Zhang Q, Gou H S, Wang P P, Shao P Z, Kobayashi Equo, Wu G H 2021 Acta Phys. Sin. 70 178101
Google Scholar
[7] Ganose A M, Park J, Faghaninia A, Woods-Robinson R, Persson K A, Jain A 2021 Nat. Commun 12 1
Google Scholar
[8] Shiojiri D, Iida T, Kadono T, Yamaguchi M, Kodama T, Yamaguchi S, Imai Y 2021 J. Appl. Phys 129 115101
Google Scholar
[9] Kohl M, Krevet B, Yeduru S R, Ezer Y, Sozinov A 2011 Smart Mater. Struct 20 094009
Google Scholar
[10] Daniel L, Rekik M, Hubert O 2014 Arch. Appl. Mech 84 1307
Google Scholar
[11] Shi P P, Zheng X J 2016 Nondestruct. Test. Eval 31 45
Google Scholar
[12] Jiles D C 1995 J. Phys. D 28 1537
Google Scholar
[13] Joule J P 1847 The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 30 76
Google Scholar
[14] Corte-Leon P, Zhukova V, Blanco J M, et al. 2021 J. Alloys Compd 855 157460
Google Scholar
[15] Zhang J M, Nie Y Z, Wang X G, Xia Q L, Guo G H 2021 J. Magn. Magn. Mater 525 167687
Google Scholar
[16] Ray R B, Kaphle G C, Rai R K, Yadav D K, Paudel R, Paudyal D 2021 J. Alloys Compd 867 158906
Google Scholar
[17] Shi P P, Su S Q, Chen Z M 2020 J. Nondestruct. Eval 39 1
Google Scholar
[18] Dubov A A 2012 Chem. Petrol. Eng 47 837
Google Scholar
[19] Tanasienko A G, Suntsov S I, Dubov A A 2002 Chem. Petrol. Eng 38 624
Google Scholar
[20] Kuleev V G, Dubov A A, Lopatin V V 2002 Russ. J. Nondestruct. Test 38 343
Google Scholar
[21] Dubov A A 2015 Metallurgist 59 164
Google Scholar
[22] 时朋朋, 郝帅 2020 70 034101
Google Scholar
Shi P P, Hao S 2020 Acta Phys. Sin. 70 034101
Google Scholar
[23] 时朋朋 2021 力学学报 70 3341
Google Scholar
Shi P P 2021 Chin. J. Theor. Appl. Mech. 70 3341
Google Scholar
[24] Yang L J, Liu B, Chen L J 2013 NDT & E Int. 55 15
Google Scholar
[25] 杨理践, 刘斌, 高松巍, 陈立佳 2013 62 086201
Google Scholar
Yang L J, Liu B, Gao S W, Chen L J 2013 Acta Phys. Sin. 62 086201
Google Scholar
[26] Essaoud S S, Jbara A S 2021 J. Magn. Magn. Mater 531 167984
Google Scholar
[27] Maskar E, Lamrani A F, Belaiche M, Es-Smairi A, Khuili M, Al-Qaisi S, Rai D P 2021 Surf. Interfaces 24 101051
Google Scholar
[28] Payne M C, Teter M P, Allan D C 1992 Rev. Mod. Phys 64 1045
Google Scholar
[29] Milman V, Winkler B, White J A 2000 Int. J. Quantum Chem 77 895
[30] Stewart J C, Matthew D S, Chris J P, Phil J H, Matt I J, Keith R, Mike C P 2005 Z. Kristallogr 220 567
Google Scholar
[31] Ernzerhof M, Scuseria G E 1999 J. Chem. Phys 110 5029
Google Scholar
[32] Marzari N, Vanderbilt D, Payne M C 1997 Phys. Rev. Lett 79 1337
Google Scholar
[33] Setyawan W, Curtarolo S 2010 Comput. Mater. Sci 49 299
Google Scholar
[34] Rahman G, Kim I G 2008 J. Magn 13 124
Google Scholar
[35] Kittel C 2021 Introduction to Solid State Physics (8th Ed.)
[36] Fang C M, Van Huis M A, Sluiter M H F, Zandbergen H W 2010 Acta Mater 58 2968
Google Scholar
-
图 1 拉伸、压缩和剪切作用引起的α-Fe磁矩(M)和能量增量(ΔE)的变化图 (a) α-Fe的2 × 2 × 2超胞在拉伸、压缩和剪切应变作用下的计算模型; (b) 磁矩变化; (c) 能量增量
Fig. 1. Variation of α-Fe magnetic moment (M) and energy increment (ΔE) induced by tension, compression and shear strain: (a) Model of α-Fe 2 × 2 × 2 supercell under tensile, compressive and shear strain; (b) Change of magnetic moment; (c) Increment of energy.
图 A1 收敛性测试 (a) 截断能收敛测试; (b) k点取值收敛测试; (c) α-Fe晶胞的能量收敛过程; (d) Fe-C(1)晶胞的能量收敛过程
Fig. A1. Convergence test: (a) Cut-off energy test; (b) k-point value test; (c) Energy convergence process of α-Fe; (d) Energy convergence process of Fe-C(1).
图 2 掺杂元素对α-Fe体系磁特性的影响 (a) 2 × 2 × 2超晶胞及掺杂1个或2个原子的掺杂体系模型; (b) 不同类型应变作用下的能量增量 ΔE; (c) 不同类型应变作用下磁矩M的变化
Fig. 2. Effect of doping elements on magnetic properties of the α-Fe system: (a) 2 × 2 × 2 supercell structure and supercell structure doped with one or two atoms; (b) Energy increments (ΔE)under different types of strain; (c) Change of magnetic moment under different types of strain.
图 3 拉伸、压缩和剪切应变作用下α-Fe的能带结构图 (a) 初始状态; (b) 5%拉应变; (c)5 %压应变; (d) 5%剪应变
Fig. 3. Band structure diagram of α-Fe under tensile, compression and shear strain: (a) Initial state; (b) 5% tensile strain; (c) 5% compressive strain; (d) 5% shear strain.
图 A3 无应变作用下α-Fe及其Fe-C和Fe-Mn掺杂体系的能带结构 (a) α-Fe; (b) Fe-C(1); (c) Fe-C(2); (d) Fe-Mn
Fig. A3. Band structure of α-Fe and its C- and Mn-doped systems without strain: (a) α-Fe; (b) Fe-C(1); (c) Fe-C(2); (d) Fe-Mn.
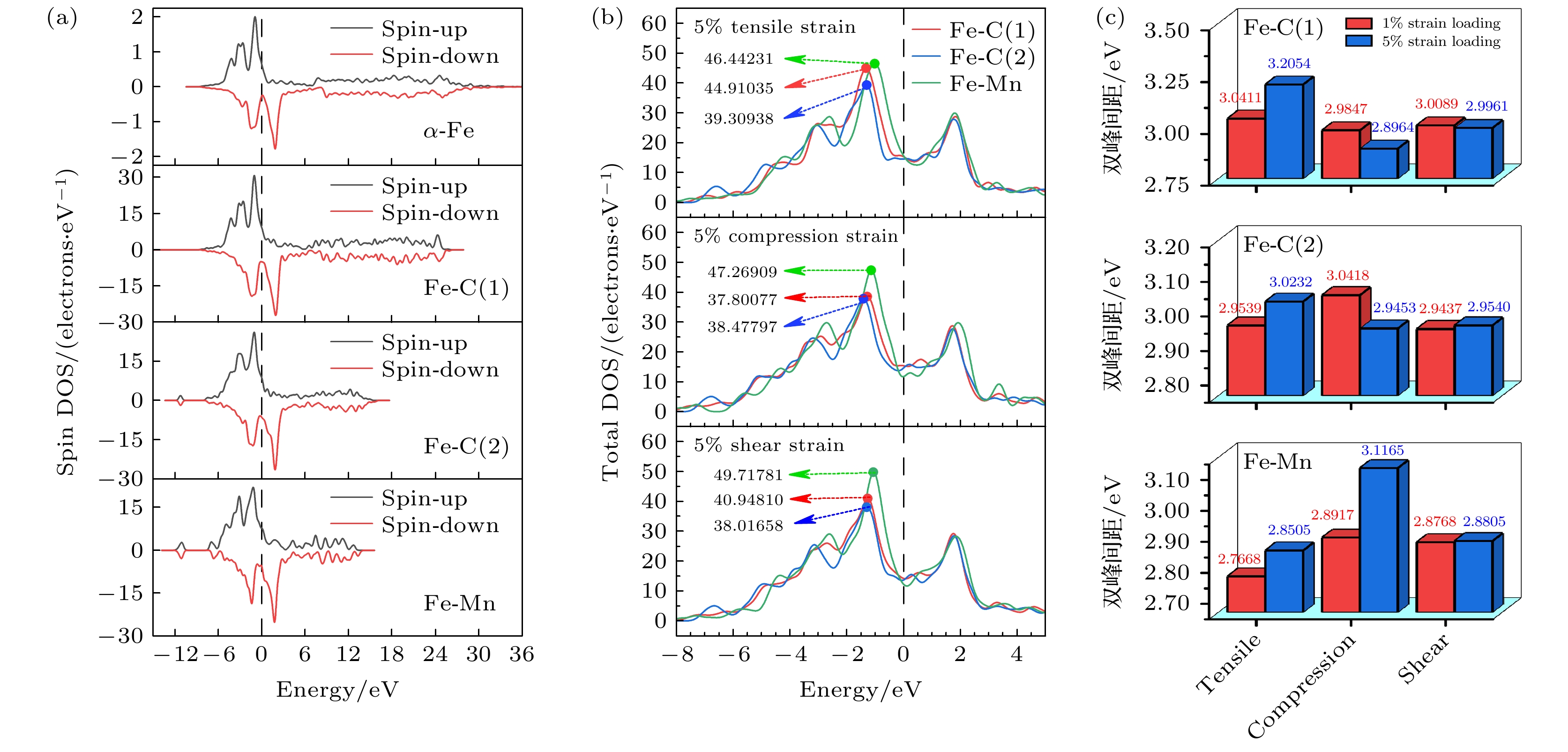
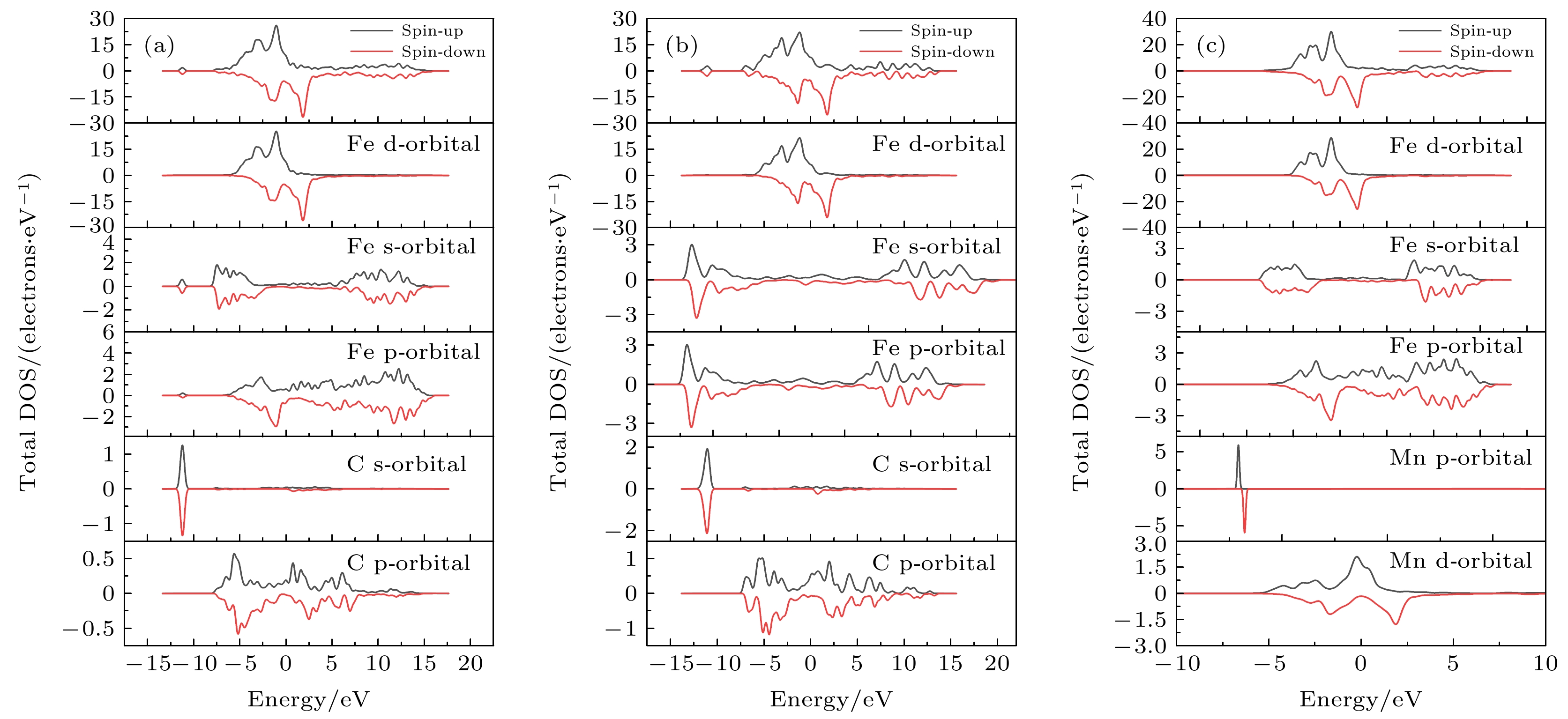
图 4 电子态密度图 (a) 不同体系自旋态密度; (b) 不同类型应变对掺杂体系DOS峰值的影响; (c) 不同类型应变加载对掺杂体系双峰间距的影响
Fig. 4. The density of states diagram: (a) Spin DOS of different systems; (b) Effects of different types of strain on DOS peaks of doping systems; (c) Effects of different types of strain loading on the spacing of double peaks in doping systems.
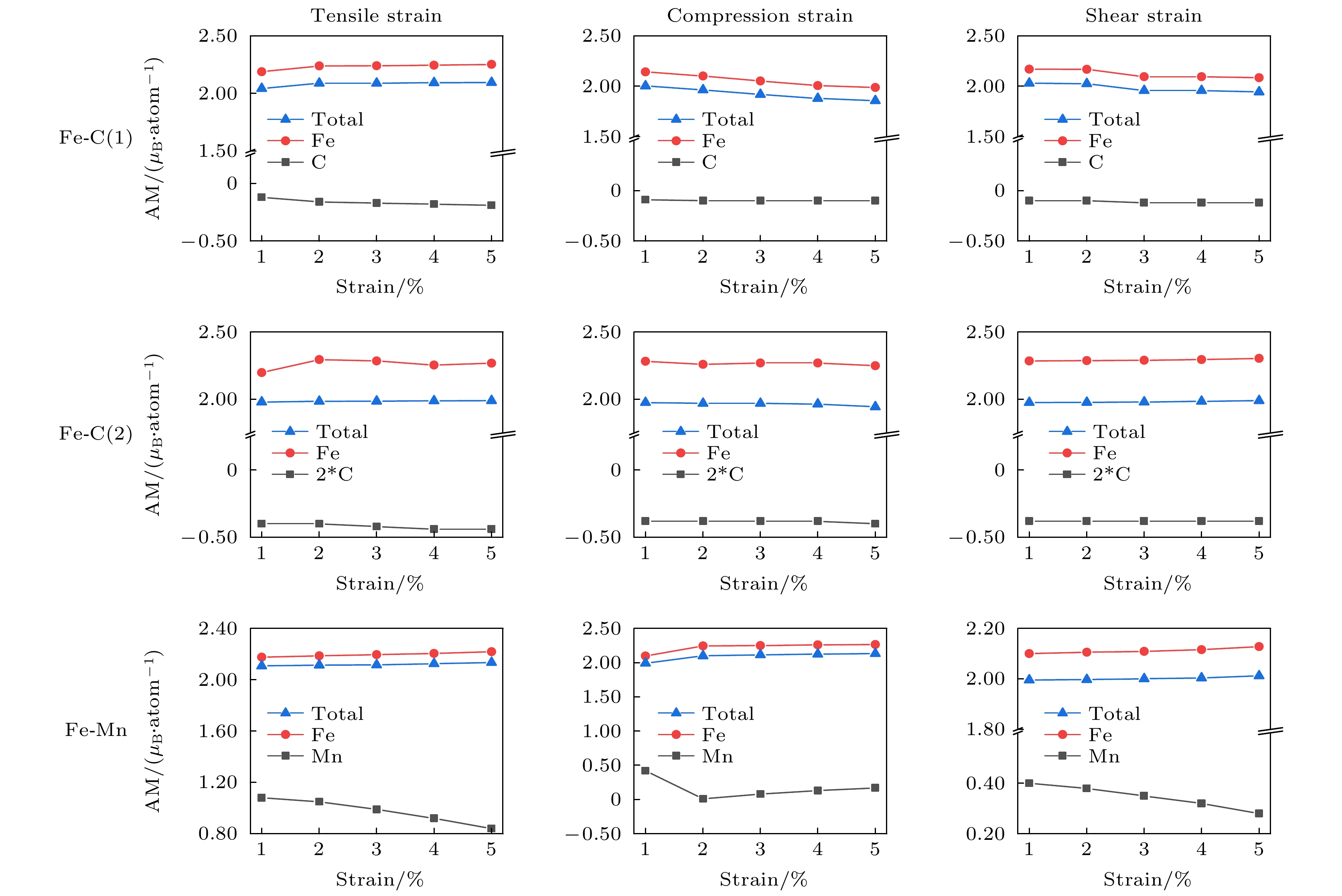
图 A5 掺杂体系在不同应变类型作用下(拉伸、压缩和剪切)的自旋态密度图 (a) Fe-C(1)体系DOS; (b) Fe-C(2)体系DOS; (c) Fe-Mn体系DOS
Fig. A5. The spin density distribution of states of doping systems under different types of strain (tensile, compression and shear strain): (a) DOS changes of Fe-C(1) doping system; (b) DOS changes of Fe-C(1) doping system; (c) DOS changes of Fe-Mn doping system.
图 5 C和Mn掺杂体系原子磁矩随三种不同应变加载方式(拉伸、压缩和剪切)的变化
Fig. 5. Variation of atomic magnetic moment with the three different types of strain loading (Tensile, compression and shear strain) for C- and Mn-doped systems.
图 A4 不同轨道电子分波态密度 (a) Fe-C(1)分波态密度; (b) Fe-C(2)分波态密度; (c) Fe-Mn分波态密度
Fig. A4. Different orbitals of PDOS: (a) PDOS of Fe-C(1); (b) PDOS of Fe-C(2); (c) PDOS of Fe-Mn.
表 A3 不同应变作用下α-Fe体系的磁矩和能量变化
Table A3. The magnetic moments and energies of a-Fe under different types of strain.
Tensile strain Compressive strain Shear strain Strain Magnetic moment/
(${\mu _{\text{B}}}{\cdot\text{ato}}{{\text{m}}^{ - 1}}$)Energy/
eVMagnetic moment/
(${\mu _{\text{B}}}{\cdot\text{ato}}{{\text{m}}^{ - 1}}$)Energy/
eVMagnetic moment/
(${\mu _{\text{B}}}{\cdot\text{ato}}{{\text{m}}^{ - 1}}$)Energy/
eV1% 2.1133 –862.9176 2.1121 –862.9178 2.1150 –862.9175 2% 2.1168 –862.9157 2.1114 –862.9163 2.1265 –862.9152 3% 2.1294 –862.9125 2.1116 –862.9157 2.1498 –862.9112 4% 2.1303 –862.9105 2.1121 –862.9126 2.1878 –862.9063 5% 2.1549 –862.9081 2.1135 –862.9097 2.2195 –862.9006 
下载: 导出CSV
表 A1 平衡态α-Fe及掺杂体系的自旋极化能
Table A1. Spin polarization energy of equilibrium α-Fe (BCC) and doping systems.
Energy state Fe(bcc) Fe-C(1) Fe-C(2) Fe-Mn spin-polarized –862.9295 –818.6694 –774.3459 –987.8903 non-spin-polarized –862.4899 –818.5050 –774.3104 –987.8903 ΔE –0.4396 –0.1644 –0.0355 –1×10–5
下载: 导出CSV
表 A2 平衡态α-Fe的晶格常数、原子体积和磁矩
Table A2. The lattice constant, atomic volume, and magnetic moment of equilibrium α-Fe(BCC).
下载: 导出CSV
表 A4 三种不同应变加载方式下掺杂体系能量的变化(eV)
Table A4. Variation of the energy in doping systems under three different types of strain loading (eV).
Strain Tensile strain Compressive strain Shear strain Fe-C(1) Fe-C(2) Fe-Mn Fe-C(1) Fe-C(2) Fe-Mn Fe-C(1) Fe-C(2) Fe-Mn 1% –818.5083 –774.3584 –987.8857 –818.5039 –774.3536 –987.9533 –818.5257 –774.3450 –987.9536 2% –818.5077 –774.3543 –987.8845 –818.4965 –774.3507 –987.9679 –818.5245 –774.3420 –987.9504 3% –818.5016 –774.3457 –987.8827 –818.4882 –774.3469 –987.9711 –818.5186 –774.3372 –987.9446 4% –818.5009 –774.3446 –987.8799 –818.4794 –774.3454 –987.9652 –818.5097 –774.3307 –987.9367 5% –818.4967 –774.3398 –987.8762 –818.4723 –774.3425 –987.9569 –818.5026 –774.3223 –987.9267
下载: 导出CSV
表 A5 不同应变作用下掺杂体系的磁矩变化
Table A5. Variation of the total magnetic moment of doping systems under different strain states (
$ {\mu }_{\mathrm{B}}) $ .Strain Tensile strain Compressive strain Shear strain Fe-C(1) Fe-C(2) Fe-Mn Fe-C(1) Fe-C(2) Fe-Mn Fe-C(1) Fe-C(2) Fe-Mn 1% 2.0433 1.9800 2.1084 2.0031 1.9753 1.9925 2.0299 1.9762 1.9959 2% 2.0887 1.9843 2.1142 1.9645 1.9693 2.1004 2.0242 1.9768 1.9974 3% 2.0887 1.9856 2.1226 1.9175 1.9694 2.1152 1.9566 1.9798 2.0006 4% 2.0927 1.9880 2.1255 1.8791 1.9642 2.1248 1.9564 1.9847 2.0037 5% 2.0952 1.9894 2.1343 1.8573 1.9436 2.1327 1.9444 1.9905 2.0118
下载: 导出CSV
-
[1] De Sousa J M, Aguiar A L, Girão E C, Fonseca A F, Souza Filho A G, Galvão D S 2021 Chem. Phys 542 111052
Google Scholar
[2] 李君, 刘立胜, 徐爽, 张金咏 2020 69 043102
Google Scholar
Li J, Liu L S, Xu S, Zhang J Y 2020 Acta Phys. Sin. 69 043102
Google Scholar
[3] Hadji S, Bouhemadou A, Haddadi K, Cherrad D, Khenata R, Bin-Omran S, Al-Douri Y 2020 Physica B 589 412213
Google Scholar
[4] Kohn W, Sham L J 1965 Phys. Rev 140 A1133
Google Scholar
[5] Han Z K, Sarker D, Ouyang R, Mazheika A, Gao Y, Levchenko S V 2021 Nat. Commun 12 1833
Google Scholar
[6] 祝平, 张强, 芶华松, 王平平, 邵溥真, 小林郁夫, 武高辉 2021 70 178101
Google Scholar
Zhu P, Zhang Q, Gou H S, Wang P P, Shao P Z, Kobayashi Equo, Wu G H 2021 Acta Phys. Sin. 70 178101
Google Scholar
[7] Ganose A M, Park J, Faghaninia A, Woods-Robinson R, Persson K A, Jain A 2021 Nat. Commun 12 1
Google Scholar
[8] Shiojiri D, Iida T, Kadono T, Yamaguchi M, Kodama T, Yamaguchi S, Imai Y 2021 J. Appl. Phys 129 115101
Google Scholar
[9] Kohl M, Krevet B, Yeduru S R, Ezer Y, Sozinov A 2011 Smart Mater. Struct 20 094009
Google Scholar
[10] Daniel L, Rekik M, Hubert O 2014 Arch. Appl. Mech 84 1307
Google Scholar
[11] Shi P P, Zheng X J 2016 Nondestruct. Test. Eval 31 45
Google Scholar
[12] Jiles D C 1995 J. Phys. D 28 1537
Google Scholar
[13] Joule J P 1847 The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 30 76
Google Scholar
[14] Corte-Leon P, Zhukova V, Blanco J M, et al. 2021 J. Alloys Compd 855 157460
Google Scholar
[15] Zhang J M, Nie Y Z, Wang X G, Xia Q L, Guo G H 2021 J. Magn. Magn. Mater 525 167687
Google Scholar
[16] Ray R B, Kaphle G C, Rai R K, Yadav D K, Paudel R, Paudyal D 2021 J. Alloys Compd 867 158906
Google Scholar
[17] Shi P P, Su S Q, Chen Z M 2020 J. Nondestruct. Eval 39 1
Google Scholar
[18] Dubov A A 2012 Chem. Petrol. Eng 47 837
Google Scholar
[19] Tanasienko A G, Suntsov S I, Dubov A A 2002 Chem. Petrol. Eng 38 624
Google Scholar
[20] Kuleev V G, Dubov A A, Lopatin V V 2002 Russ. J. Nondestruct. Test 38 343
Google Scholar
[21] Dubov A A 2015 Metallurgist 59 164
Google Scholar
[22] 时朋朋, 郝帅 2020 70 034101
Google Scholar
Shi P P, Hao S 2020 Acta Phys. Sin. 70 034101
Google Scholar
[23] 时朋朋 2021 力学学报 70 3341
Google Scholar
Shi P P 2021 Chin. J. Theor. Appl. Mech. 70 3341
Google Scholar
[24] Yang L J, Liu B, Chen L J 2013 NDT & E Int. 55 15
Google Scholar
[25] 杨理践, 刘斌, 高松巍, 陈立佳 2013 62 086201
Google Scholar
Yang L J, Liu B, Gao S W, Chen L J 2013 Acta Phys. Sin. 62 086201
Google Scholar
[26] Essaoud S S, Jbara A S 2021 J. Magn. Magn. Mater 531 167984
Google Scholar
[27] Maskar E, Lamrani A F, Belaiche M, Es-Smairi A, Khuili M, Al-Qaisi S, Rai D P 2021 Surf. Interfaces 24 101051
Google Scholar
[28] Payne M C, Teter M P, Allan D C 1992 Rev. Mod. Phys 64 1045
Google Scholar
[29] Milman V, Winkler B, White J A 2000 Int. J. Quantum Chem 77 895
[30] Stewart J C, Matthew D S, Chris J P, Phil J H, Matt I J, Keith R, Mike C P 2005 Z. Kristallogr 220 567
Google Scholar
[31] Ernzerhof M, Scuseria G E 1999 J. Chem. Phys 110 5029
Google Scholar
[32] Marzari N, Vanderbilt D, Payne M C 1997 Phys. Rev. Lett 79 1337
Google Scholar
[33] Setyawan W, Curtarolo S 2010 Comput. Mater. Sci 49 299
Google Scholar
[34] Rahman G, Kim I G 2008 J. Magn 13 124
Google Scholar
[35] Kittel C 2021 Introduction to Solid State Physics (8th Ed.)
[36] Fang C M, Van Huis M A, Sluiter M H F, Zandbergen H W 2010 Acta Mater 58 2968
Google Scholar
下载:
计量
- 文章访问数: 4663
- PDF下载量: 93
- 被引次数: 0
