-
光电倍增管(photomultiplier tubes, PMT)具有光子级别的灵敏度、低暗计数、低后脉冲概率, 被广泛应用于可见光波段的光子计数雷达中. PMT没有光子探测死区时间, 每响应一个光子就会输出一个电子流脉冲, 这些电子流脉冲有可能堆成规模更大的脉冲, 使用阈值鉴别法鉴别光子事件时, 堆叠的脉冲会引入额外的脉冲行走误差. 考虑到脉冲堆叠的影响, 建立了新的PMT光子探测理论模型, 并通过蒙特卡罗仿真, 得到了基于PMT的光子计数测距法的行走误差、测距精度和回波激光脉宽, PMT输出电子流脉宽以及光子事件鉴别阈值之间的关系. 搭建了基于PMT的激光雷达系统, 通过与GM-APD的对比实验证明了脉冲堆叠对PMT光子计数法测距存在不可忽略的影响. 考虑到脉冲堆叠的PMT光子探测模型能够指导基于PMT的光子计数雷达的设计, 提高测距系统的测距精度和准度.Photomultiplier tube (PMT) features single photon level sensitivity, low dark count, and low afterpulse probability, and are widely used in photon-counting lidar in the visible spectrum. The PMT has no photon detection dead time, for every photon it responds to, it can output an electron flow pulse, these pulses of electron flow are likely to pile up into larger pulses. When using threshold identification method to identify photon-events, the stacked pulse will introduce additional pulse walking error, directly affecting the ranging precision of photon-counting ranging method in the practical application of laser ranging. Considering the influence of pulse pile-up, a new theoretical model of PMT photon detection is established to describe the influence of pulse pile-up on the detection probability of photon-events by analyzing the relationship between the detection time of photon and the identification time of the PMT final output photon-events. Through Monte Carlo simulation, the relationship among the ranging walking error, ranging accuracy, incident laser pulse width, PMT output electron flow pulse width and photon-events identification threshold is obtained. In order to verify the correctness of the theory, a PMT-based photon-counting lidar system is built. The comparative experiment with GM-APD proves that the influence of pulse pile-up on PMT photon-counting ranging method cannot be ignored, and that the experimental results are in good agreement with results from the theoretical model. The PMT photon detection model based on pulse pile-up can guide the design of PMT photon-counting radar and improve the ranging accuracy and precision of the ranging system.
-
Keywords:
- photomultiplier tubes /
- pulse pile-up /
- photon-counting /
- ranging
[1] Degnan J 2016 Remote Sens. 8 958
Google Scholar
[2] Massa J S, Wallace A M, Buller G S, Fancey S J, Walker A C 1997 Opt. Lett. 22 543
Google Scholar
[3] Kirmani A, Venkatraman D, Shin D, Colaco A, Wong F N C, Shapiro J H, Goyal V K 2014 Science 343 58
Google Scholar
[4] Maccarone A, McCarthy A, Ren X, Warburton R E, Wallace A M, Moffat J, Petillot Y, Buller G S 2015 Opt. Express 23 33911
Google Scholar
[5] Li Z, Lai J, Wang C, Yan W, Li Z 2017 Appl. Opt. 56 6680
Google Scholar
[6] Akiba M, Inagaki K, Tsujino K 2012 Opt. Express 20 2779
Google Scholar
[7] Ravil A 2018 Appl. Opt. 57 3679
Google Scholar
[8] Kitsmiller V J, Campbell C, O'Sullivan T D 2020 Biomed. Opt. Express 11 5373
Google Scholar
[9] Jones R, Oliver C, Pike E R 1971 Appl. Opt. 10 1673
Google Scholar
[10] McGill M, Markus T, Scott V. S, Neumann T 2013 J. Atmos. Oceanic Technol. 30 345
Google Scholar
[11] Abdalati W, Zwally H. J, Bindschadler R, Csatho B, Farrell S L, Fricker H A, Harding D, Kwok R, Lefsky M, Markus T, Marshak A, Neumann T, Palm S, Schutz B, Smith B, Spinhirne J, Webb C, 2010 Proc. IEEE 98 735
Google Scholar
[12] Markus T, Neumann T, Martino A, Abdalati W, Brunt K, Csatho B, Farrell S, Fricker H, Gardner A, Harding D, Jasinski M, Kwok R, Magruder L, Lubin D, Luthcke S, Morison J, Nelson R, Neuenschwander A, Palm S, Popescu S, Shum C, B. Schutz E, Smith B, Yang Y, Zwally J 2017 Remote Sens. Environ. 190 260
Google Scholar
[13] Helstrom C W 1984 J. Appl. Phys. 55 2786
Google Scholar
[14] Ingle J D, Crouch S R 1972 Anal. Chem. 44 777
Google Scholar
[15] 谢庚承, 叶一东, 李建民, 袁学文 2018 中国激光 45 260
Google Scholar
Xie G C, Ye Y D, Li J M, Yuan X W 2018 Chinese Journal of Lasers 45 260
Google Scholar
[16] Donovan D P, Whiteway J A, Carswell I A 1993 Appl. Opt. 32 6742
Google Scholar
[17] Chen Z D, Li X D, Li X H, Ye G C, Zhou Z G 2019 Opt. Commun. 434 7
Google Scholar
[18] Zhang Z Y, Li S, Ma Y, Zhang W H, Zhao P F, Xiang Y Y 2020 Optics Express. 28 13586
Google Scholar
[19] Gatt P, Johnson S, Nichols T 2009 Appl. Opt. 48 3261
Google Scholar
[20] Li S, Zhang Z, Ma Y, Zeng H M, Zhao P F, Zhang W H 2019 Opt. Express 27 A861
Google Scholar
[21] White Book of Photomultiplier Tubes, Hamamatsu Photonics http://share.hamamatsu.com.cn/57f4441b72a94d8a91500e56afad0b7b/download.html [2022-07-18]
[22] 黄科, 李松, 马跃, 田昕, 周辉, 张智宇 2018 67 064205
Google Scholar
Huang K, Li S, Ma Y, Tian X, Zhou H, Zhang Z Y 2018 Acta Phys. Sin. 67 064205
Google Scholar
-
图 1 PMT输出电子流脉冲叠加对光子事件鉴别的影响
Fig. 1. Influence of PMT output electron flow pulse pile-up on photon-events discrimination.
图 2 (a) 回波光子数为1时, PMT光子事件鉴别时间与电子流脉冲峰值时间存在系统误差
$ \gamma $ ; (b)蓝色曲线和橙色曲线分别为PMT响应$ {\mu _1} $ ,$ {\mu _2} $ 时刻到达的光子输出的电子流脉冲, 黄色曲线为两个脉冲的叠加,$ {w_{\left( {{\mu _1}, {\mu _2}} \right)}} $ 为$ {\mu _1} $ ,$ {\mu _2} $ 时刻的电子流脉冲叠加产生的脉冲行走误差Fig. 2. (a) When the number of incident photons is 1, there is a systematic error
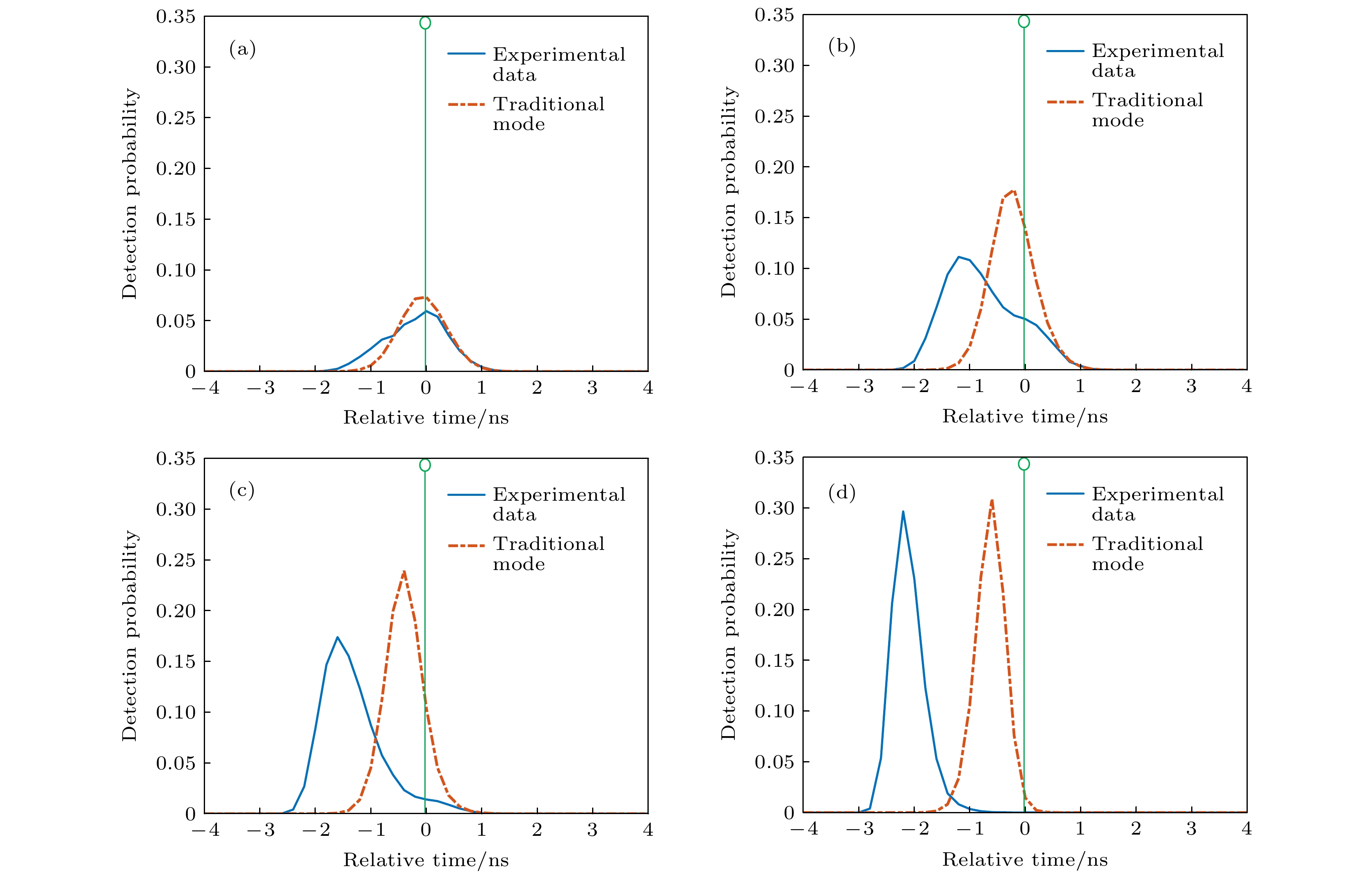
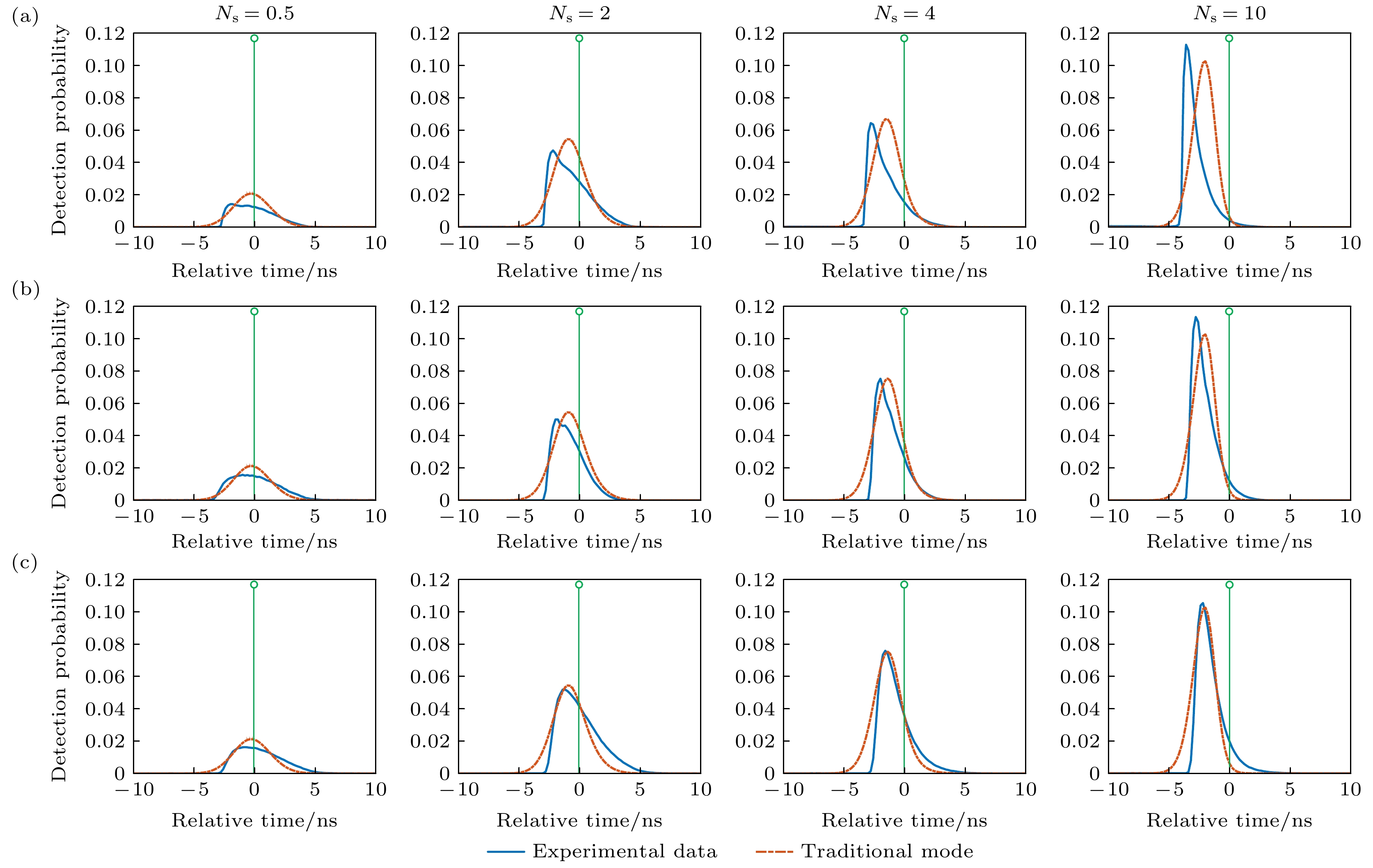
$ \gamma $ between the PMT photon-events identification time and the peak time of electron flow pulse; (b) the blue curve and the orange curve are the electron flow pulses output responsed by PMT for the photon arriving at time$ {\mu _1} $ and$ {\mu _2} $ respectively. The yellow curve is the pile-up of two pulses, and$ {w_{\left( {{\mu _1}, {\mu _2}} \right)}} $ is the pulse walk error generated by the pile-up of the tow electron flow pulses at time$ {\mu _1} $ and$ {\mu _2} $ .
图 3 PMT单光子探测模型与传统单光子探测模型概率分布的区别 (a) Ns = 0.5; (b) Ns = 2; (c) Ns = 4; (d) Ns = 10
Fig. 3. Difference of probability distribution between PMT single-photon detection model and traditional single-photon detection model: (a) Ns = 0.5; (b) Ns = 2; (c) Ns = 4; (d) Ns = 10.
图 4 PMT单光子探测模型和传统单光子探测模型关于测距行走误差Ra和测距精度 Rp的比较
Fig. 4. Comparison between PMT single-photon detection model and traditional single-photon detection model on ranging walking error Ra and ranging accuracy Rp.
图 5 不同电子流高斯脉宽
$ {\delta _{\text{p}}} $ 条件下PMT探测模型测距行走误差Ra和测距精度 Rp与入射信号光子数的关系Fig. 5. Relationship of ranging walk error Ra and ranging accuracy Rp of PMT detection model to incident signal photon number under different Gaussian pulse width
$ {\delta _{\text{p}}} $ of electron flow.
图 6 PMT探测模型测距行走误差Ra和测距精度 Rp与光子事件鉴别阈值
$ {T_{\text{h}}} $ 的关系Fig. 6. Relationship of the ranging walking error Ra and ranging accuracy Rp of the PMT detection model to the identification threshold of photon-events
图 8 (a)无射频放大器光子事件鉴别电路; (b)带射频放大器光子事件鉴别电路
Fig. 8. (a) Photon-events identification circuit without RF amplifier; (b) photon-events identification circuit with RF amplifier.
图 9 (a) PMT输出脉冲归一化幅值与平均入射信号光子数的关系; (b) APD测得的回波信号脉冲
Fig. 9. (a) Relationship between PMT output pulse normalized amplitude and average number of incident signal photon; (b) incident signal pulse measured by APD.
图 10 (a)带RF放大器的PMT探测概率分布随入射信号光子数的变化; (b)不带RF放大器的PMT探测概率分布随入射信号光子数的变化; (c) GM-APD探测概率分布随入射信号光子数的变化
Fig. 10. (a) Experimental results of PMT detection probability distribution with RF amplifier varying with the number of incident signal photons; (b) experimental results of PMT detection probability distribution without RF amplifier varying with the number of incident signal photons; (c) experimental results of GM-APD detection probability distribution varying with the number of incident signal photons.
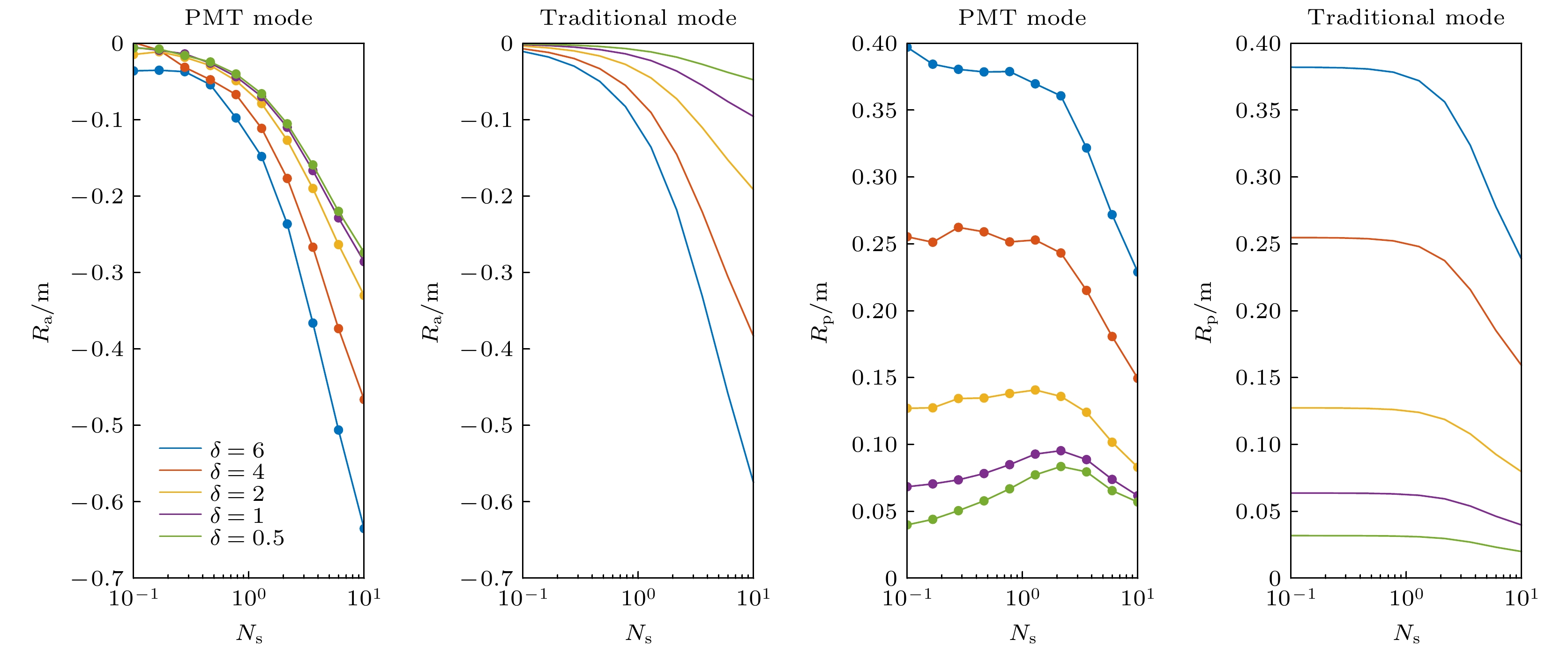
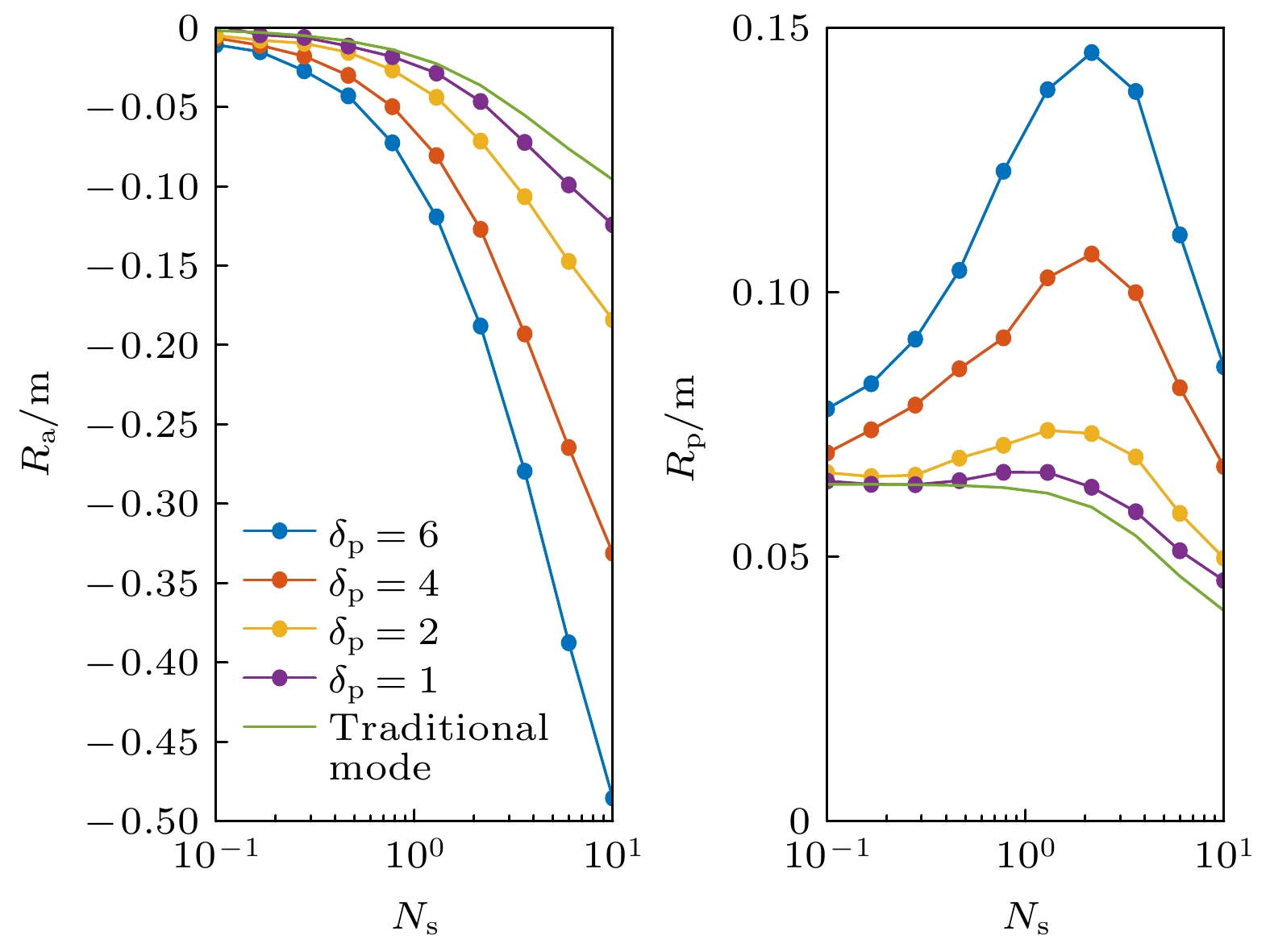
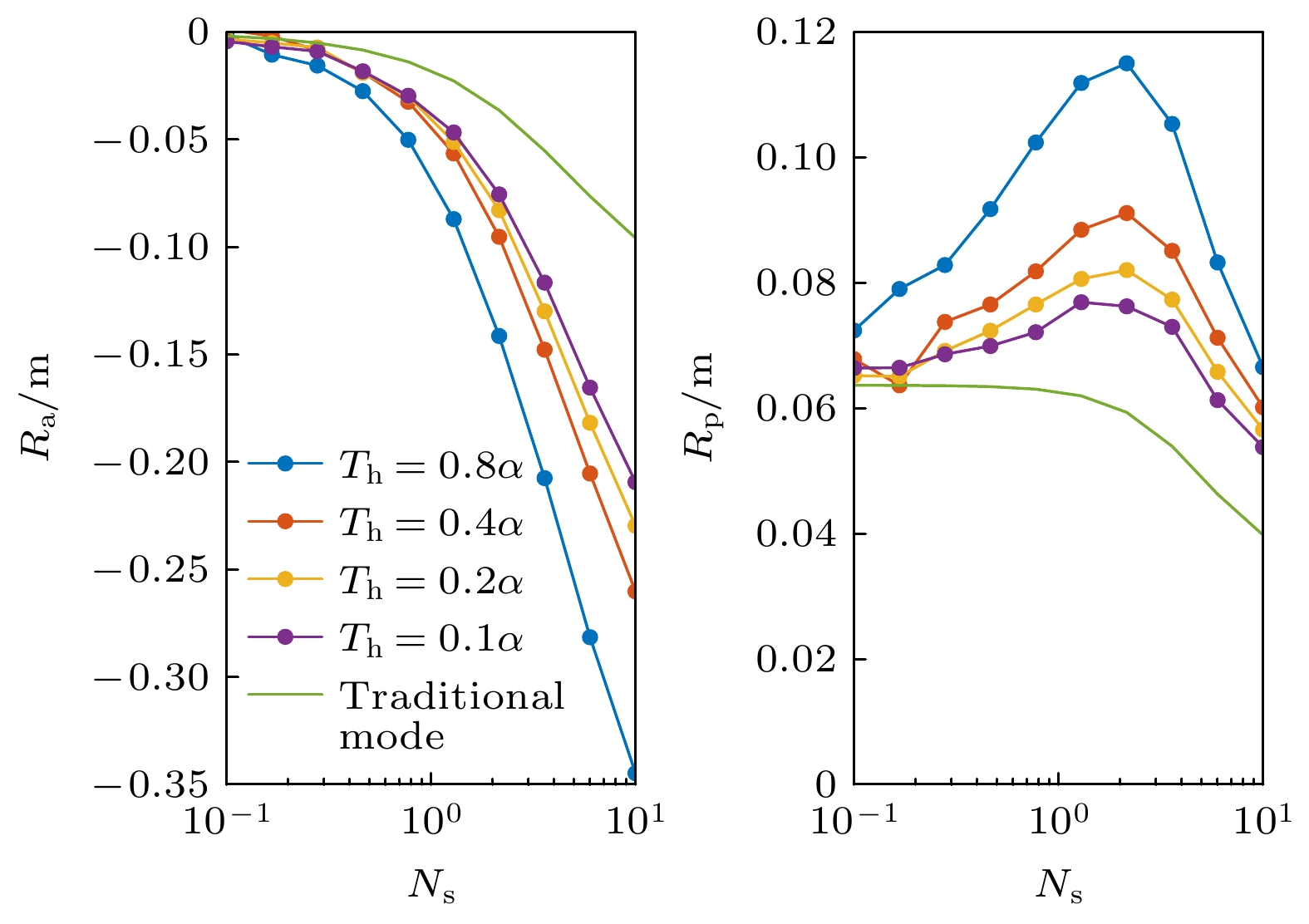
图 11 (a)带RF放大器的PMT探测概率分布随入射信号光子数的变化仿真实验结果; (b)不带RF放大器的PMT探测概率分布随入射信号光子数的变化仿真实验结果
Fig. 11. (a) Simulation results of PMT detection probability distribution with RF amplifier varying with photon number of incident signal; (b) simulation results of PMT detection probability distribution without RF amplifier varying with photon number of incident signal.
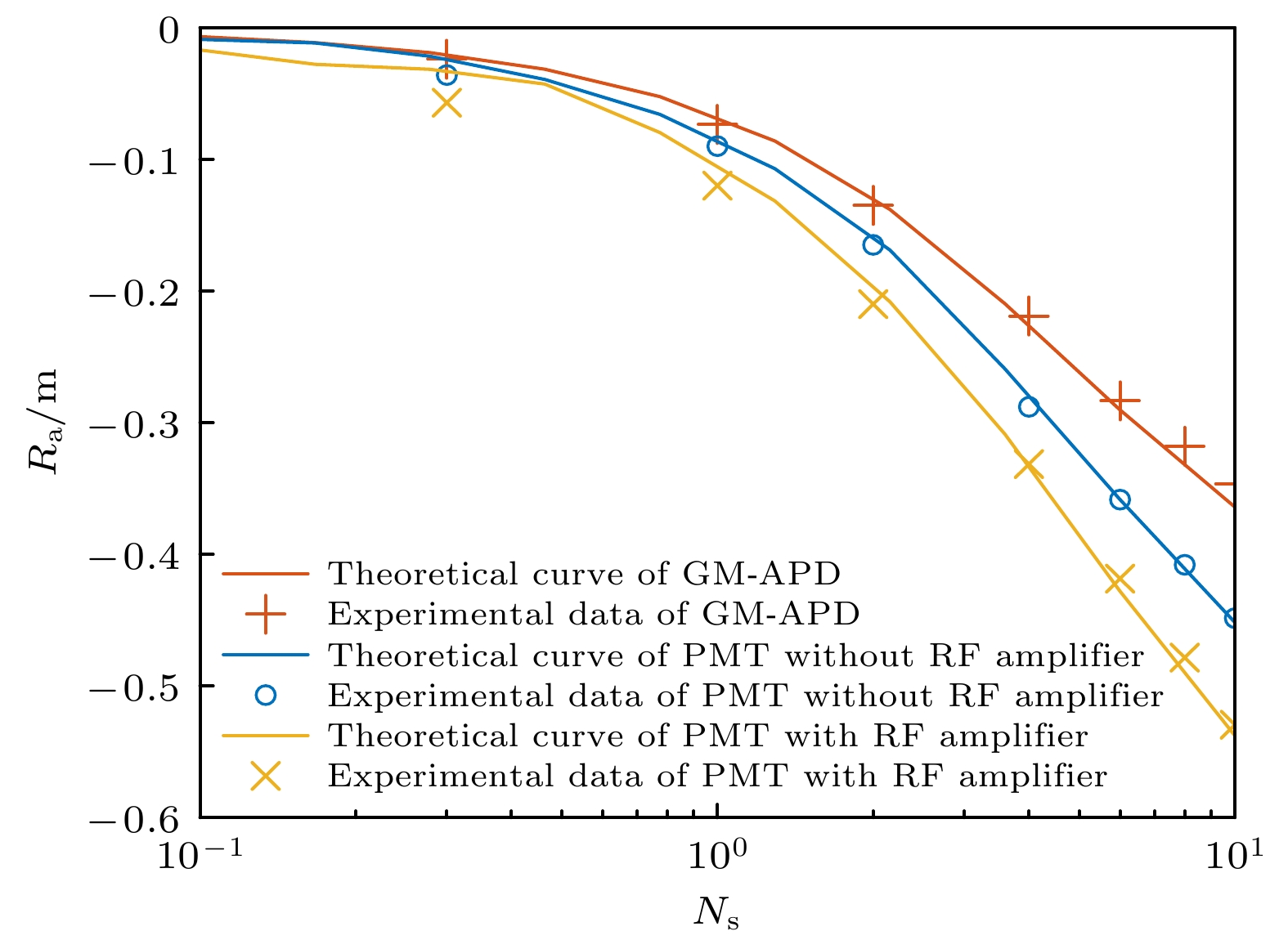
图 12 三种探测器的测距行走误差的仿真模型和实验数据对比, 橙色实线为GM-APD的Ra理论探测曲线, 橙色“+”为GM-APD的Ra实验数据点; 蓝色实线为不带放大器PMT的Ra理论探测曲线, 蓝色“o”为不带RF放大器的PMT的 Ra实验数据点; 黄色实线为带RF放大器PMT的Ra理论探测曲线, 黄色“x”为带RF放大器PMT的Ra实验数据点
Fig. 12. Comparison of the simulation model and experimental data of the ranging walking error of the three detectors. The solid orange line is the Ra theoretial curve of GM-APD, and the orange “+” is the Ra experimental data point of GM-APD. The blue solid line is the Ra theoretial curve of PMT without RF amplifier, and the blue “o” is the Ra experimental data point of PMT without RF amplifier. The solid yellow line is Ra theoretial curve of PMT with RF amplifier, and the yellow “x” is Ra experimental data point of PMT with RF amplifier.
表 1 PMT和GM-APD模块性能参数
Table 1. Parameters of PMT and GM-APD module
探测器 PMT GM-APD 增益 106—107 105—106 探测效率(640 nm)/% 18 20 暗计数(counts) <30 <500 探测死区时间/ns 20 50 时间抖动/ps <200 <500 
下载: 导出CSV
-
[1] Degnan J 2016 Remote Sens. 8 958
Google Scholar
[2] Massa J S, Wallace A M, Buller G S, Fancey S J, Walker A C 1997 Opt. Lett. 22 543
Google Scholar
[3] Kirmani A, Venkatraman D, Shin D, Colaco A, Wong F N C, Shapiro J H, Goyal V K 2014 Science 343 58
Google Scholar
[4] Maccarone A, McCarthy A, Ren X, Warburton R E, Wallace A M, Moffat J, Petillot Y, Buller G S 2015 Opt. Express 23 33911
Google Scholar
[5] Li Z, Lai J, Wang C, Yan W, Li Z 2017 Appl. Opt. 56 6680
Google Scholar
[6] Akiba M, Inagaki K, Tsujino K 2012 Opt. Express 20 2779
Google Scholar
[7] Ravil A 2018 Appl. Opt. 57 3679
Google Scholar
[8] Kitsmiller V J, Campbell C, O'Sullivan T D 2020 Biomed. Opt. Express 11 5373
Google Scholar
[9] Jones R, Oliver C, Pike E R 1971 Appl. Opt. 10 1673
Google Scholar
[10] McGill M, Markus T, Scott V. S, Neumann T 2013 J. Atmos. Oceanic Technol. 30 345
Google Scholar
[11] Abdalati W, Zwally H. J, Bindschadler R, Csatho B, Farrell S L, Fricker H A, Harding D, Kwok R, Lefsky M, Markus T, Marshak A, Neumann T, Palm S, Schutz B, Smith B, Spinhirne J, Webb C, 2010 Proc. IEEE 98 735
Google Scholar
[12] Markus T, Neumann T, Martino A, Abdalati W, Brunt K, Csatho B, Farrell S, Fricker H, Gardner A, Harding D, Jasinski M, Kwok R, Magruder L, Lubin D, Luthcke S, Morison J, Nelson R, Neuenschwander A, Palm S, Popescu S, Shum C, B. Schutz E, Smith B, Yang Y, Zwally J 2017 Remote Sens. Environ. 190 260
Google Scholar
[13] Helstrom C W 1984 J. Appl. Phys. 55 2786
Google Scholar
[14] Ingle J D, Crouch S R 1972 Anal. Chem. 44 777
Google Scholar
[15] 谢庚承, 叶一东, 李建民, 袁学文 2018 中国激光 45 260
Google Scholar
Xie G C, Ye Y D, Li J M, Yuan X W 2018 Chinese Journal of Lasers 45 260
Google Scholar
[16] Donovan D P, Whiteway J A, Carswell I A 1993 Appl. Opt. 32 6742
Google Scholar
[17] Chen Z D, Li X D, Li X H, Ye G C, Zhou Z G 2019 Opt. Commun. 434 7
Google Scholar
[18] Zhang Z Y, Li S, Ma Y, Zhang W H, Zhao P F, Xiang Y Y 2020 Optics Express. 28 13586
Google Scholar
[19] Gatt P, Johnson S, Nichols T 2009 Appl. Opt. 48 3261
Google Scholar
[20] Li S, Zhang Z, Ma Y, Zeng H M, Zhao P F, Zhang W H 2019 Opt. Express 27 A861
Google Scholar
[21] White Book of Photomultiplier Tubes, Hamamatsu Photonics http://share.hamamatsu.com.cn/57f4441b72a94d8a91500e56afad0b7b/download.html [2022-07-18]
[22] 黄科, 李松, 马跃, 田昕, 周辉, 张智宇 2018 67 064205
Google Scholar
Huang K, Li S, Ma Y, Tian X, Zhou H, Zhang Z Y 2018 Acta Phys. Sin. 67 064205
Google Scholar
下载:
计量
- 文章访问数: 4129
- PDF下载量: 77
- 被引次数: 0
