-
利用量子态的叠加性和纠缠, 量子计算为显著地加速经典算法, 例如大数分解、求解线性方程组、量子多体系统模拟等问题, 提供了可能. 随着量子计算机硬件的快速发展, 探索量子计算超越经典计算极限方向的研究受到了越来越多的重视. 针对一类特定的问题, 现有的量子设备已经展现出超越经典计算机的能力. 但由于一些量子算法(诸如大数分解等问题)需要依赖于一个通用的大规模的容错的量子计算机, 考虑到现阶段的量子设备的量子比特数十分有限, 且容易与环境发生退相干, 近期的研究主要集中在探索基于含噪声的中等规模量子设备以及浅层量子线路的量子优越性. 一些采样问题被作为演示量子优越性的候选项提出. 本文介绍和总结了几个可以在现阶段的量子设备上实现的量子优越性问题, 并就其中两个备受关注的量子优越性问题—随机量子线路模拟和玻色采样及其衍生的采样问题的理论和实验进展、经典模拟算法等展开讨论. 随着上述两类量子优越性问题在超导和光学量子平台的实现, 我们预期当前和近期的量子设备将解决更多问题, 从而实现更一般的量子优势.Exploiting the coherence and entanglement of quantum many-qubit states, quantum computing can significantly surpass classical algorithms, making it possible to factor large numbers, solve linear equations, simulate many-body quantum systems, etc., in a reasonable time. With the rapid development of quantum computing hardware, many attention has been drawn to explore how quantum computers could go beyond the limit of classical computation. Owing to the need of a universal fault-tolerant quantum computer for many existing quantum algorithms, such as Shor’s factoring algorithm, and considering the limit of near-term quantum devices with small qubit numbers and short coherence times, many recent works focused on the exploration of demonstrating quantum advantages using noisy intermediate-scaled quantum devices and shallow circuits, and hence some sampling problems have been proposed as the candidates for quantum advantage demonstration. This review summarizes quantum advantage problems that are realizable on current quantum hardware. We focus on two notable problems—random circuit simulation and boson sampling—and consider recent theoretical and experimental progresses. After the respective demonstrations of these two types of quantum advantages on superconducting and optical quantum platforms, we expect current and near-term quantum devices could be employed for demonstrating quantum advantages in general problems.
-
Keywords:
- quantum advantages /
- random circuit sampling /
- Boson sampling /
- classical simulation
[1] [2] Harrow A W, Hassidim A, Lloyd S 2009 Phys. Rev. Lett. 103 150502
Google Scholar
[3] Nielsen M A, Chuang I 2002 Quantum Computation and Quantum Information (New York: Cambridge University Press) pp171–216
[4] Babbush R, Gidney C, Berry D W, Wiebe N, McClean J, Paler A, Fowler A, Neven H 2018 Phys. Rev. X 8 041015
Google Scholar
[5] Harrow A W, Montanaro A 2017 Nature 549 203
Google Scholar
[6] Boixo S, Isakov S V, Smelyanskiy V N, Babbush R, Ding N, Jiang Z, Bremner M J, Martinis J M, Neven H 2018 Nat. Phys. 14 595
Google Scholar
[7] Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505
Google Scholar
[8] Shepherd D, Bremner M J 2009 Proc. Math. Phys. Eng. Sci. 465 1413
Google Scholar
[9] Aaronson S, Arkhipov A 2011 Proceedings of the Forty-third Annual ACM Symposium on Theory of Computing San Jose, California, USA, June 6–8, 2011 p333
[10] Lund A P, Laing A, Rahimi-Keshari S, Rudolph T, O’Brien J L, Ralph T C 2014 Phys. Rev. Lett. 113 100502
Google Scholar
[11] Hamilton C S, Kruse R, Sansoni L, Barkhofen S, Silberhorn C, Jex I 2017 Phys. Rev. Lett. 119 170501
Google Scholar
[12] Wang H, Li W, Jiang X, He Y M, Li Y H, Ding X, Chen M C, Qin J, Peng C Z, Schneider C, Kamp M, Zhang W J, Li H, You L X, Wang Z, Dowling J P, Höfling S, Lu C Y, Pan J W 2018 Phys. Rev. Lett. 120 230502
Google Scholar
[13] Zhou W H, Gao J, Jiao Z Q, Wang X W, Ren R J, Pang X L, Qiao L F, Zhang C N, Yang T H, Jin X M 2020 arXiv: 2009.03327[quant-ph]
[14] Knill E, Laflamme R 1998 Phys. Rev. Lett. 81 5672
Google Scholar
[15] Morimae T, Fujii K, Fitzsimons J F 2014 Phys. Rev. Lett. 112 130502
Google Scholar
[16] Fujii K, Kobayashi H, Morimae T, Nishimura H, Tamate S, Tani S 2016 43rd International Colloquium on Automata, Languages, and Programming Rome, Italy, July 11–15, 2016 p13
[17] Wu Y L, Bao W S, Cao S R, et al. 2021 arXiv: 2106.14734 [quant-ph]
[18] Zhu Q L, Cao S R, Chen F S, et al. 2021 arXiv: 2109.03494v2 [quant-ph]
[19] Pednault E, Gunnels J A, Nannicini G, Horesh L, Magerlein T, Solomonik E, Wisnieff R 2017 arXiv: 1710.05867[quant-ph]
[20] Boixo S, Isakov S V, Smelyanskiy V N, Neven H 2017 arXiv: 1712.05384[quant-ph]
[21] Chen J X, Zhang F, Huang C, Newman M, Shi Y Y 2018 arXiv: 1805.01450[quant-ph]
[22] Li R L, Wu B J, Ying M S, Sun X M, Yang G W 2019 IEEE Trans. Parallel Distrib. Syst. 31 805
Google Scholar
[23] Chen Z Y, Zhou Q, Xue C, Yang X, Guo G C, Guo G P 2018 Sci. Bull. 63 964
Google Scholar
[24] Chen M C, Li R L, Gan L, Zhu X B, Yang G W, Lu C Y, Pan J W 2020 Phys. Rev. Lett. 124 080502
Google Scholar
[25] Zhang F, Huang C, Newman M, Cai J J, Yu H J, Tian Z X, Yuan B, Xu H H, Wu J Y, Gao X, Chen J X, Szegedy M, Shi Y Y 2019 arXiv: 1907.11217[quant-ph]
[26] Pednault E, Gunnels J A, Nannicini G, Horesh L, Wisnieff R 2019 arXiv: 1910.09534[quant-ph]
[27] Huang C, Zhang F, Newman M, Cai J J, Gao X, Tian Z X, Wu J Y, Xu H H, Yu H J, Yuan B, Szegedy M, Shi Y Y, Chen J X 2020 arXiv: 2005.06787[quant-ph]
[28] Pan F, Zhang P 2021 arXiv: 2103.03074[quant-ph]
[29] Bremner M J, Jozsa R, Shepherd D J 2011 Proc. Math. Phys. Eng. Sci. 467 459
Google Scholar
[30] Bremner M J, Montanaro A, Shepherd D J 2016 Phys. Rev. Lett. 117 080501
Google Scholar
[31] Douce T, Markham D, Kashefi E, Diamanti E, Coudreau T, Milman P, Loock P V, Ferrini G 2017 Phys. Rev. Lett. 118 070503
Google Scholar
[32] Arrazola J M, Rebentrost P, Weedbrook C 2017 arXiv: 1712.07288[quant-ph]
[33] Huh J, Yung M H 2017 Sci. Rep. 7 1
Google Scholar
[34] Arrazola J M, Bromley T R 2018 Phys. Rev. Lett. 121 030503
Google Scholar
[35] Schuld M, Brádler K, Israel R, Su D, Gupt B 2019 Phys. Rev. A 101 032314
Google Scholar
[36] Brádler K, Friedland S, Izaac J, Killoran N, Su D Q 2021 Spec. Matrices 9 166
Google Scholar
[37] Brádler K, Dallaire-Demers P L, Rebentrost P, Su D Q, Weedbrook C 2018 Phys. Rev. A 98 032310
Google Scholar
[38] Arrazola J M, Bromley T R, Rebentrost P 2018 Phys. Rev. A 98 012322
Google Scholar
[39] Banchi L, Fingerhuth M, Babej T, Ing C, Arrazola J M 2020 Sci. Adv. 6 eaax1950
Google Scholar
[40] Jahangiri S, Arrazola J M, Quesada N, Killoran N 2020 Phys. Rev. E 101 022134
Google Scholar
[41] Quesada N, Arrazola J M, Killoran N 2018 Phys. Rev. A 98 062322
Google Scholar
[42] Broome M A, Fedrizzi A, Rahimi-Keshari S, Dove J, Aaronson S, Ralph T C, White A G 2013 Science 339 794
Google Scholar
[43] Carolan J, Meinecke J D A, Shadbolt P J, Russell N J, Ismail N, Wörhoff K, Rudolph T, Thompson M G, O'brien J L, Matthews J C, Laing A 2014 Nat. Photonics 8 621
Google Scholar
[44] Tillmann M, Dakić B, Heilmann R, Nolte S, Szameit A, Walther P 2013 Nat. Photonics 7 540
Google Scholar
[45] Crespi A, Osellame R, Ramponi R, Brod D J, Galvao E F, Spagnolo N, Vitelli C, Maiorino E, Mataloni P, Sciarrino F 2013 Nat. Photonics 7 545
Google Scholar
[46] Spagnolo N, Vitelli C, Bentivegna M, Brod D J, Crespi A, Flamini F, Giacomini S, Milani G, Ramponi R, Mataloni P, Osellame R, Galvao F E, Sciarrino F 2014 Nat. Photonics 8 615
Google Scholar
[47] Spring J B, Metcalf B J, Humphreys P C, Kolthammer W S, Jin X M, Barbieri M, Datta A, Thomas-Peter N, Langford N K, Kundys D, Gates J C, Smith B J, Smith P G, Walmsley I A 2013 Science 339 798
Google Scholar
[48] Su D Q, Myers C R, Sabapathy K K 2019 Phys. Rev. A 100 052301
Google Scholar
[49] Zhong H S, Peng L C, Li Y, Hu Y, Li W, Qin J, Wu D, Zhang W J, Li H, Zhang L, Wang Z, You L X, Jiang X, Li L, Liu N L, Dowling J P, Lu C Y, Pan J W 2019 Sci. Bull. 64 511
Google Scholar
[50] Barkhofen S, Bartley T J, Sansoni L, Kruse R, Hamilton C S, Jex I, Silberhorn C 2017 Phys. Rev. Lett. 118 020502
Google Scholar
[51] Wang H, Qin J, Ding X, Chen M C, Chen S, You X, He Y M, Jiang X, You L, Wang Z, Schneider C, Renema J J, Höfling S, Lu C Y, Pan J W 2019 Phys. Rev. Lett. 123 250503
Google Scholar
[52] Bentivegna M, Spagnolo N, Vitelli C, Flamini F, Viggianiello N, Latmiral L, Mataloni P, Brod D J, Galvão E F, Crespi A, Ramponi R, Osellame R, Sciarrino F 2015 Sci. Adv. 1 e1400255
Google Scholar
[53] Zhong H S, Wang H, Deng Y H, Chen M C, Peng L C, Luo Y H, Qin J, Wu D, Ding X, Hu Y, Hu P, Yang X Y, Zhang W J, Li H, Li Y X, Jiang X, Gan L, Yang G W, You L X, Wang Z, Li L, Liu N L, Lu C Y, Pan J W 2020 Science 370 1460
Google Scholar
[54] Neville A, Sparrow C, Clifford R, Johnston E, Birchall P M, Montanaro A, Laing A 2017 Nat. Phys. 13 1153
Google Scholar
[55] Clifford P, Clifford R 2018 Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms New Orleans, Louisiana, USA, January 7–10, 2018 p146
[56] Wu B J, Cheng B, Zhang J L, Yung M H, Sun X M 2020 Sci. Bull. 65 832
Google Scholar
[57] Quesada N, Chadwick R S, Bell B A, Arrazola J M, Vincent T, Qi H Y, García-Patrón R 2020 arXiv: 2010.15595[quant-ph]
[58] Aaronson S, Chen L J 2016 arXiv: 1612.05903[quant-ph]
[59] Aaronson S, Gunn S 2019 arXiv: 1910.12085[quant-ph]
[60] Lund A P, Bremner M J, Ralph T C 2017 NPJ Quantum Inf. 3 1
Google Scholar
[61] Fujii K, Tamate S 2016 Sci. Rep. 6 1
Google Scholar
[62] Bremner M J, Montanaro A, Shepherd D J 2017 Quantum 1 8
Google Scholar
[63] Kruse R, Hamilton C S, Sansoni L, Barkhofen S, Silberhorn C, Jex I 2018 Phys. Rev. A 100 032326
Google Scholar
[64] Valiant L G 1979 Theor. Comput. Sci. 8 189
Google Scholar
[65] Björklund A, Gupt B, Quesada N 2019 J. Exp. Algorithmics 24 1
Google Scholar
[66] Markov I L, Shi Y Y 2008 SIAM J. Sci. Comput. 38 963
Google Scholar
[67] Gray J, Kourtis S 2020 Quantum 5 410
Google Scholar
[68] Wu J, Liu Y, Zhang B, Jin X, Wang Y, Wang H, Yang X 2018 Nat. Sci. Rev. 5 715
Google Scholar
[69] Li Y X, Chen M C, Chen Y J, Lu H T, Gan L, Lu C Y, Pan J W, Fu H H, Yang G W 2020 arXiv: 2009.01177[quant-ph]
[70] Quesada N, Arrazola J M 2019 Phys. Rev. Res. 2 023005
Google Scholar
[71] Harrigan M P, Sung K J, Neeley M, et al. 2021 Nat. Phys. 17 332
Google Scholar
[72] Arute F, Arya K, Babbush R, et al. 2000 Science 369 1084
Google Scholar
[73] Arute F, Arya K, Babbush R, et al. 2010 arXiv: 2010.07965 [quant-ph]
[74] Liu Y, Arunachalam S, Temme K 2021 Nat. Phys. 17 1013
Google Scholar
[75] Huang H Y, Kueng R, Preskill J 2021 Phys. Rev. Lett. 126 190505
Google Scholar
-
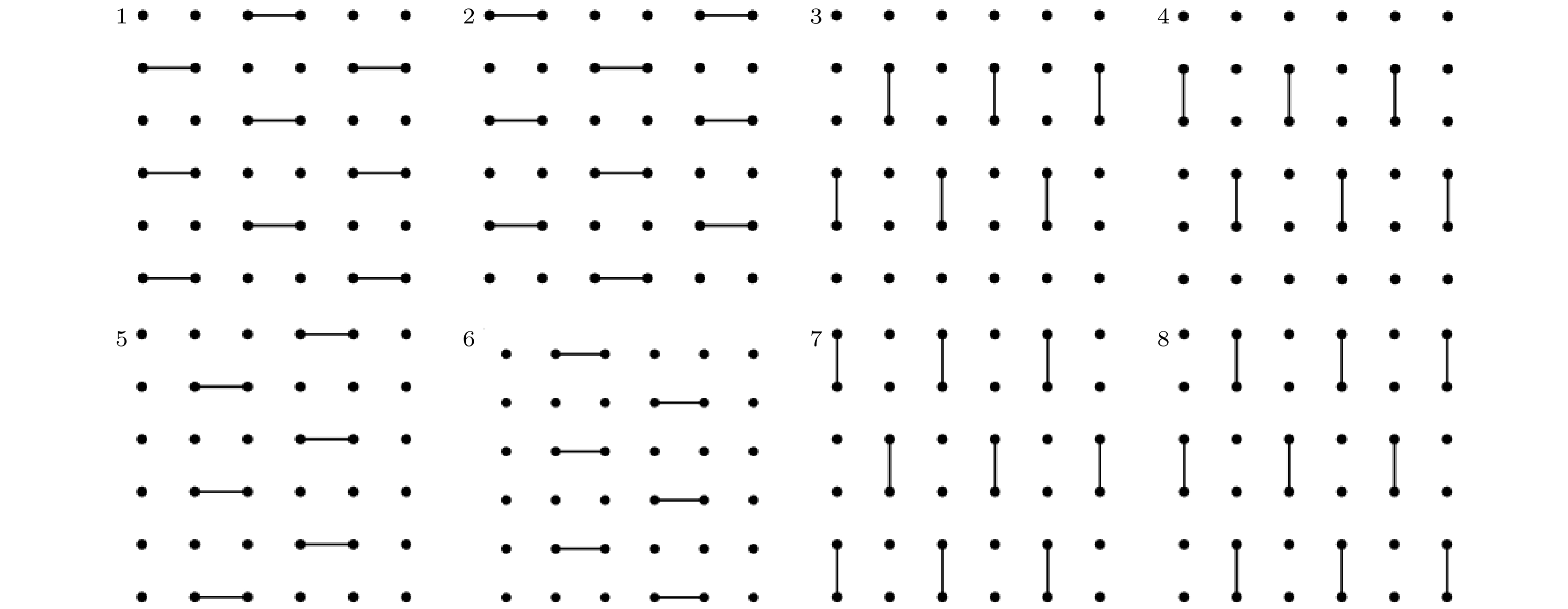
图 1 随机线路的CNOT门的8种不同的摆放方式[6]. 其中第0层全部摆放H门, 电路中每8层循环一次(重复图中1—8层), 空白节点处随机放置
$ {\boldsymbol I}, {\boldsymbol T}, {\boldsymbol X}^{1/2}, {\boldsymbol Y}^{1/2} $ 门, 两比特门为CZ门Fig. 1. Eight different layouts of the CNOT gate in the random circuit, where all of qubits are performed H gate in the
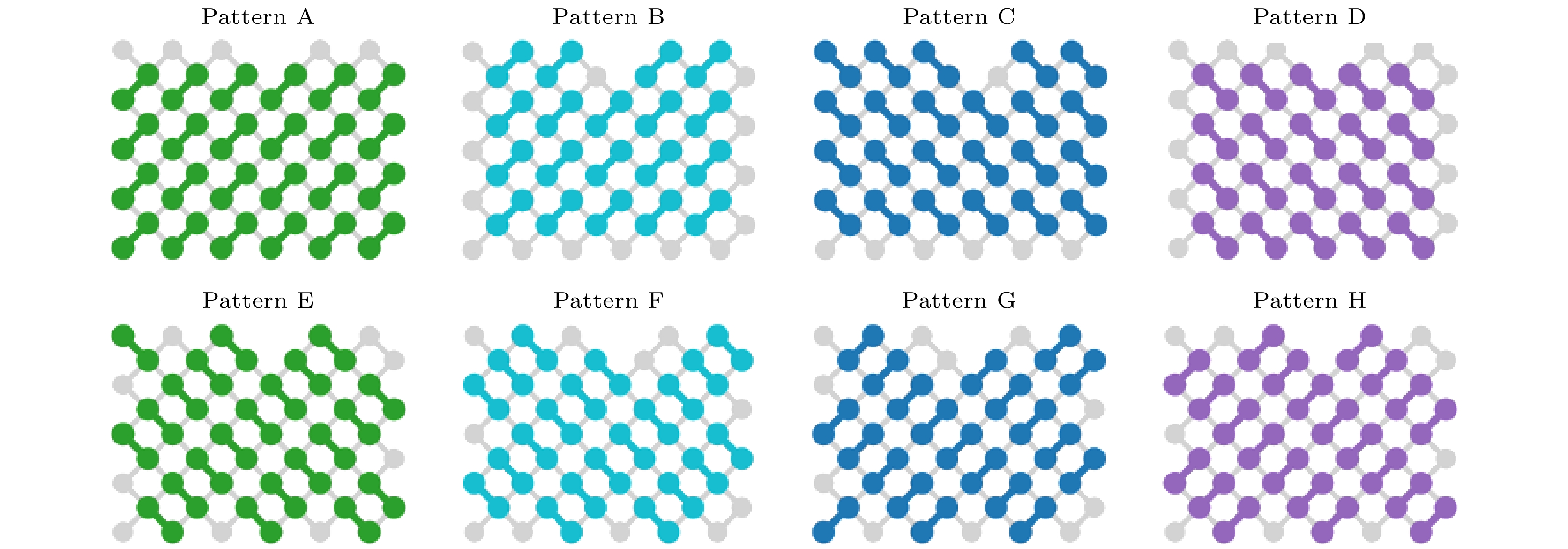
$ 0 $ -th layer, and cycle once every 8 layers in the circuit (repeat 1–8 layers of this graph), the blank vertices are laid out$ {\boldsymbol I}, {\boldsymbol T}, {\boldsymbol X}^{1/2}, {\boldsymbol Y}^{1/2} $ randomly, and the two-qubit gates are all CZ gates[6].
图 2 悬铃木处理器随机线路架构[7]. 其中第0层全部摆放H门, 电路每层迭代重复模式ABCDCDBA, 两个模式中间由一层随机放置的单比特门
$ {\boldsymbol X}^{1/2},\; {\boldsymbol Y}^{1/2},\;{\boldsymbol W}^{1/2} $ 构成, 两比特门为控制相位门和部分$ i $ SWAP门的乘积(部分$ i $ SWAP门后跟随一个控制相位门构成)Fig. 2. Random circuit architecture for Sycamore processor, where all of qubits are performed H gates in the
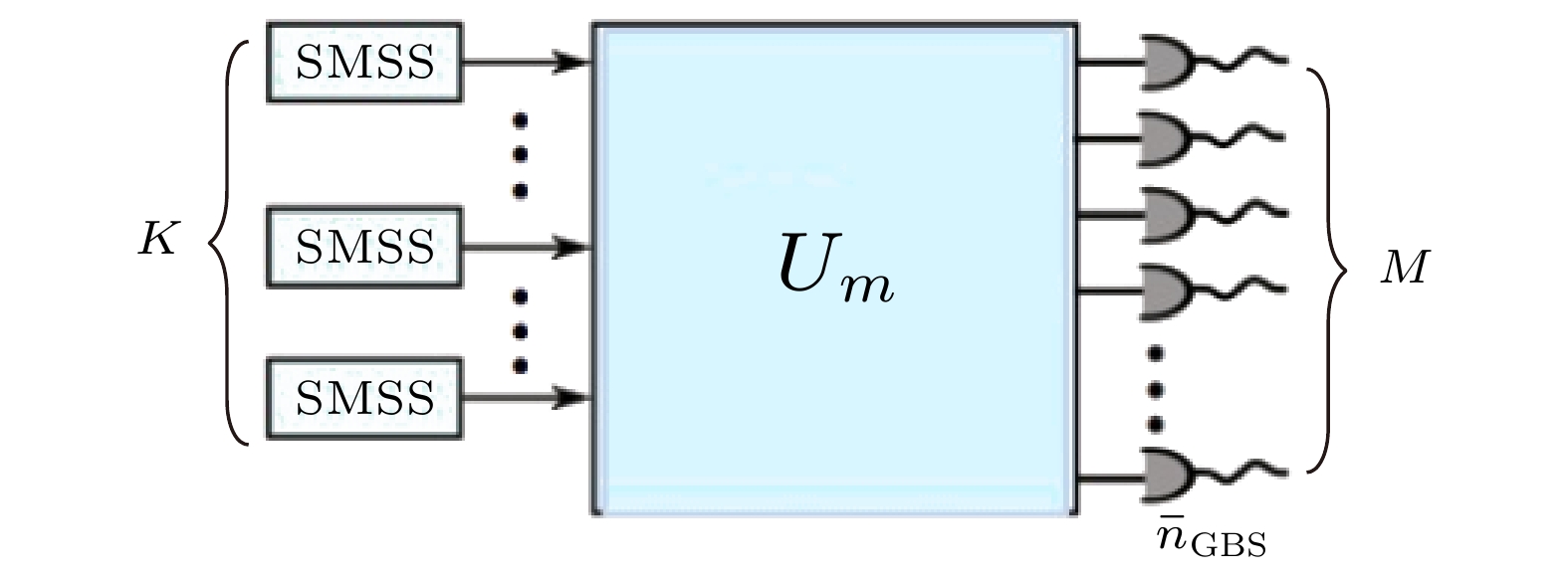
$ 0 $ -th layer, the layer of the circuit iterates and repeats the pattern ABCDCDBA, a layer of random single-qubit gates are performed between two modes, which constructed by$ {\boldsymbol X}^{1/2},\;{\boldsymbol Y}^{1/2},\; {\boldsymbol W}^{1/2} $ , the two-qubit gate is the multiplication of the partial-iSWAP gate and control-phase gate (constructed by partial-iSWAP gate followed by a control-phase gate)[7].
图 4 SBS的装置简介[63]. 该模型中输入为
$ 2 m $ 个单模压缩态, 在其进入分束器和相移子装置后产生双模压缩态, 并通过一个额外的测量装置来固定SBS的线性光学装置$ \boldsymbol{U}_m $ 输入的光子数Fig. 4. Brief introduction of SBS device[63]. In this model, the input are
$ 2 m $ single-mode compressed states, and the two-mode compressed states are generated after entering the beam splitter and the phase-shifting sub-device. An additional measuring device is used to fix the number of input photons for the linear optical device$ \boldsymbol{U}_m $ of SBS.
图 6 量子优越性证明的实验结果[7] (a)在经典可验证区, 简单全量子线路的保真度与简单删减量子线路、简单分割量子线路、简单乘积模型的保真度符合得很好, 每个数据点是多个随机量子线路采样的平均值; (b)在量子优越区, 通过更简单的线路和简单乘积模型来估计复杂全量子线路的保真度. 红色时间标志表示经典模拟复杂全量子线路的验证任务需要的时间, 灰色时间标志表示经典模拟相应的采样任务需要的时间
Fig. 6. Experimental results of the proof of quantum advantage[7]: (a) In the classical verifiable region, the fidelity of simple full quantum circuit accords well with that of simple truncated quantum circuit, simple split quantum circuit and simple product model. Each data point is the average of multiple random quantum circuit samples. (b) In the quantum advantage region, the fidelity of complex full quantum circuits is estimated by using simpler circuits and simple product models. The red time label represents the time required for the verification task of the classical simulation complex full quantum circuit, and the grey time label represents the time required for the corresponding sampling task of the classical simulation.
-
[1] [2] Harrow A W, Hassidim A, Lloyd S 2009 Phys. Rev. Lett. 103 150502
Google Scholar
[3] Nielsen M A, Chuang I 2002 Quantum Computation and Quantum Information (New York: Cambridge University Press) pp171–216
[4] Babbush R, Gidney C, Berry D W, Wiebe N, McClean J, Paler A, Fowler A, Neven H 2018 Phys. Rev. X 8 041015
Google Scholar
[5] Harrow A W, Montanaro A 2017 Nature 549 203
Google Scholar
[6] Boixo S, Isakov S V, Smelyanskiy V N, Babbush R, Ding N, Jiang Z, Bremner M J, Martinis J M, Neven H 2018 Nat. Phys. 14 595
Google Scholar
[7] Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505
Google Scholar
[8] Shepherd D, Bremner M J 2009 Proc. Math. Phys. Eng. Sci. 465 1413
Google Scholar
[9] Aaronson S, Arkhipov A 2011 Proceedings of the Forty-third Annual ACM Symposium on Theory of Computing San Jose, California, USA, June 6–8, 2011 p333
[10] Lund A P, Laing A, Rahimi-Keshari S, Rudolph T, O’Brien J L, Ralph T C 2014 Phys. Rev. Lett. 113 100502
Google Scholar
[11] Hamilton C S, Kruse R, Sansoni L, Barkhofen S, Silberhorn C, Jex I 2017 Phys. Rev. Lett. 119 170501
Google Scholar
[12] Wang H, Li W, Jiang X, He Y M, Li Y H, Ding X, Chen M C, Qin J, Peng C Z, Schneider C, Kamp M, Zhang W J, Li H, You L X, Wang Z, Dowling J P, Höfling S, Lu C Y, Pan J W 2018 Phys. Rev. Lett. 120 230502
Google Scholar
[13] Zhou W H, Gao J, Jiao Z Q, Wang X W, Ren R J, Pang X L, Qiao L F, Zhang C N, Yang T H, Jin X M 2020 arXiv: 2009.03327[quant-ph]
[14] Knill E, Laflamme R 1998 Phys. Rev. Lett. 81 5672
Google Scholar
[15] Morimae T, Fujii K, Fitzsimons J F 2014 Phys. Rev. Lett. 112 130502
Google Scholar
[16] Fujii K, Kobayashi H, Morimae T, Nishimura H, Tamate S, Tani S 2016 43rd International Colloquium on Automata, Languages, and Programming Rome, Italy, July 11–15, 2016 p13
[17] Wu Y L, Bao W S, Cao S R, et al. 2021 arXiv: 2106.14734 [quant-ph]
[18] Zhu Q L, Cao S R, Chen F S, et al. 2021 arXiv: 2109.03494v2 [quant-ph]
[19] Pednault E, Gunnels J A, Nannicini G, Horesh L, Magerlein T, Solomonik E, Wisnieff R 2017 arXiv: 1710.05867[quant-ph]
[20] Boixo S, Isakov S V, Smelyanskiy V N, Neven H 2017 arXiv: 1712.05384[quant-ph]
[21] Chen J X, Zhang F, Huang C, Newman M, Shi Y Y 2018 arXiv: 1805.01450[quant-ph]
[22] Li R L, Wu B J, Ying M S, Sun X M, Yang G W 2019 IEEE Trans. Parallel Distrib. Syst. 31 805
Google Scholar
[23] Chen Z Y, Zhou Q, Xue C, Yang X, Guo G C, Guo G P 2018 Sci. Bull. 63 964
Google Scholar
[24] Chen M C, Li R L, Gan L, Zhu X B, Yang G W, Lu C Y, Pan J W 2020 Phys. Rev. Lett. 124 080502
Google Scholar
[25] Zhang F, Huang C, Newman M, Cai J J, Yu H J, Tian Z X, Yuan B, Xu H H, Wu J Y, Gao X, Chen J X, Szegedy M, Shi Y Y 2019 arXiv: 1907.11217[quant-ph]
[26] Pednault E, Gunnels J A, Nannicini G, Horesh L, Wisnieff R 2019 arXiv: 1910.09534[quant-ph]
[27] Huang C, Zhang F, Newman M, Cai J J, Gao X, Tian Z X, Wu J Y, Xu H H, Yu H J, Yuan B, Szegedy M, Shi Y Y, Chen J X 2020 arXiv: 2005.06787[quant-ph]
[28] Pan F, Zhang P 2021 arXiv: 2103.03074[quant-ph]
[29] Bremner M J, Jozsa R, Shepherd D J 2011 Proc. Math. Phys. Eng. Sci. 467 459
Google Scholar
[30] Bremner M J, Montanaro A, Shepherd D J 2016 Phys. Rev. Lett. 117 080501
Google Scholar
[31] Douce T, Markham D, Kashefi E, Diamanti E, Coudreau T, Milman P, Loock P V, Ferrini G 2017 Phys. Rev. Lett. 118 070503
Google Scholar
[32] Arrazola J M, Rebentrost P, Weedbrook C 2017 arXiv: 1712.07288[quant-ph]
[33] Huh J, Yung M H 2017 Sci. Rep. 7 1
Google Scholar
[34] Arrazola J M, Bromley T R 2018 Phys. Rev. Lett. 121 030503
Google Scholar
[35] Schuld M, Brádler K, Israel R, Su D, Gupt B 2019 Phys. Rev. A 101 032314
Google Scholar
[36] Brádler K, Friedland S, Izaac J, Killoran N, Su D Q 2021 Spec. Matrices 9 166
Google Scholar
[37] Brádler K, Dallaire-Demers P L, Rebentrost P, Su D Q, Weedbrook C 2018 Phys. Rev. A 98 032310
Google Scholar
[38] Arrazola J M, Bromley T R, Rebentrost P 2018 Phys. Rev. A 98 012322
Google Scholar
[39] Banchi L, Fingerhuth M, Babej T, Ing C, Arrazola J M 2020 Sci. Adv. 6 eaax1950
Google Scholar
[40] Jahangiri S, Arrazola J M, Quesada N, Killoran N 2020 Phys. Rev. E 101 022134
Google Scholar
[41] Quesada N, Arrazola J M, Killoran N 2018 Phys. Rev. A 98 062322
Google Scholar
[42] Broome M A, Fedrizzi A, Rahimi-Keshari S, Dove J, Aaronson S, Ralph T C, White A G 2013 Science 339 794
Google Scholar
[43] Carolan J, Meinecke J D A, Shadbolt P J, Russell N J, Ismail N, Wörhoff K, Rudolph T, Thompson M G, O'brien J L, Matthews J C, Laing A 2014 Nat. Photonics 8 621
Google Scholar
[44] Tillmann M, Dakić B, Heilmann R, Nolte S, Szameit A, Walther P 2013 Nat. Photonics 7 540
Google Scholar
[45] Crespi A, Osellame R, Ramponi R, Brod D J, Galvao E F, Spagnolo N, Vitelli C, Maiorino E, Mataloni P, Sciarrino F 2013 Nat. Photonics 7 545
Google Scholar
[46] Spagnolo N, Vitelli C, Bentivegna M, Brod D J, Crespi A, Flamini F, Giacomini S, Milani G, Ramponi R, Mataloni P, Osellame R, Galvao F E, Sciarrino F 2014 Nat. Photonics 8 615
Google Scholar
[47] Spring J B, Metcalf B J, Humphreys P C, Kolthammer W S, Jin X M, Barbieri M, Datta A, Thomas-Peter N, Langford N K, Kundys D, Gates J C, Smith B J, Smith P G, Walmsley I A 2013 Science 339 798
Google Scholar
[48] Su D Q, Myers C R, Sabapathy K K 2019 Phys. Rev. A 100 052301
Google Scholar
[49] Zhong H S, Peng L C, Li Y, Hu Y, Li W, Qin J, Wu D, Zhang W J, Li H, Zhang L, Wang Z, You L X, Jiang X, Li L, Liu N L, Dowling J P, Lu C Y, Pan J W 2019 Sci. Bull. 64 511
Google Scholar
[50] Barkhofen S, Bartley T J, Sansoni L, Kruse R, Hamilton C S, Jex I, Silberhorn C 2017 Phys. Rev. Lett. 118 020502
Google Scholar
[51] Wang H, Qin J, Ding X, Chen M C, Chen S, You X, He Y M, Jiang X, You L, Wang Z, Schneider C, Renema J J, Höfling S, Lu C Y, Pan J W 2019 Phys. Rev. Lett. 123 250503
Google Scholar
[52] Bentivegna M, Spagnolo N, Vitelli C, Flamini F, Viggianiello N, Latmiral L, Mataloni P, Brod D J, Galvão E F, Crespi A, Ramponi R, Osellame R, Sciarrino F 2015 Sci. Adv. 1 e1400255
Google Scholar
[53] Zhong H S, Wang H, Deng Y H, Chen M C, Peng L C, Luo Y H, Qin J, Wu D, Ding X, Hu Y, Hu P, Yang X Y, Zhang W J, Li H, Li Y X, Jiang X, Gan L, Yang G W, You L X, Wang Z, Li L, Liu N L, Lu C Y, Pan J W 2020 Science 370 1460
Google Scholar
[54] Neville A, Sparrow C, Clifford R, Johnston E, Birchall P M, Montanaro A, Laing A 2017 Nat. Phys. 13 1153
Google Scholar
[55] Clifford P, Clifford R 2018 Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms New Orleans, Louisiana, USA, January 7–10, 2018 p146
[56] Wu B J, Cheng B, Zhang J L, Yung M H, Sun X M 2020 Sci. Bull. 65 832
Google Scholar
[57] Quesada N, Chadwick R S, Bell B A, Arrazola J M, Vincent T, Qi H Y, García-Patrón R 2020 arXiv: 2010.15595[quant-ph]
[58] Aaronson S, Chen L J 2016 arXiv: 1612.05903[quant-ph]
[59] Aaronson S, Gunn S 2019 arXiv: 1910.12085[quant-ph]
[60] Lund A P, Bremner M J, Ralph T C 2017 NPJ Quantum Inf. 3 1
Google Scholar
[61] Fujii K, Tamate S 2016 Sci. Rep. 6 1
Google Scholar
[62] Bremner M J, Montanaro A, Shepherd D J 2017 Quantum 1 8
Google Scholar
[63] Kruse R, Hamilton C S, Sansoni L, Barkhofen S, Silberhorn C, Jex I 2018 Phys. Rev. A 100 032326
Google Scholar
[64] Valiant L G 1979 Theor. Comput. Sci. 8 189
Google Scholar
[65] Björklund A, Gupt B, Quesada N 2019 J. Exp. Algorithmics 24 1
Google Scholar
[66] Markov I L, Shi Y Y 2008 SIAM J. Sci. Comput. 38 963
Google Scholar
[67] Gray J, Kourtis S 2020 Quantum 5 410
Google Scholar
[68] Wu J, Liu Y, Zhang B, Jin X, Wang Y, Wang H, Yang X 2018 Nat. Sci. Rev. 5 715
Google Scholar
[69] Li Y X, Chen M C, Chen Y J, Lu H T, Gan L, Lu C Y, Pan J W, Fu H H, Yang G W 2020 arXiv: 2009.01177[quant-ph]
[70] Quesada N, Arrazola J M 2019 Phys. Rev. Res. 2 023005
Google Scholar
[71] Harrigan M P, Sung K J, Neeley M, et al. 2021 Nat. Phys. 17 332
Google Scholar
[72] Arute F, Arya K, Babbush R, et al. 2000 Science 369 1084
Google Scholar
[73] Arute F, Arya K, Babbush R, et al. 2010 arXiv: 2010.07965 [quant-ph]
[74] Liu Y, Arunachalam S, Temme K 2021 Nat. Phys. 17 1013
Google Scholar
[75] Huang H Y, Kueng R, Preskill J 2021 Phys. Rev. Lett. 126 190505
Google Scholar
下载:
计量
- 文章访问数: 7684
- PDF下载量: 422
- 被引次数: 0
