-
科研人员近年来提出了石墨烯热电子能量转换器件(graphene thermionic energy converter, GTEC)的模型, 对其物理机理与参数优化展开了研究, 为高品位热能开发提供了新途径. 然而, 空间电荷积累和近场热辐射效应对GTEC能量转换性能的影响却鲜有报道. 本文结合热电子发射、朗缪尔空间电荷、非平衡态热力学和涨落电动力学等理论, 考虑热电子输运、近场热辐射输运、牛顿换热的相互作用对GETC的影响, 进而构建完善的物理模型. 首先, 分析极板温度恒定时的电流密度、阴极板附加势垒、功率密度、转换效率、热流对电压和真空间隙的依赖特性, 结果表明真空间隙对功率密度的影响显著, 而对效率的影响较小, 可在不同的电压处获得最高功率密度和效率. 其次, 分析了极板温度受能量平衡约束条件下, 功率密度与效率随电压的变化情况, 研究发现: 相比于恒温模型, 牛顿换热对功率密度的影响显著, 而对效率的影响较小; 在最优功率密度时的阳极板温度高于环境温度, 而最优效率时的阳极板温度趋于环境温度; 折衷考虑功率密度和效率, 确定了电压、真空间隙和阳极板温度的优化区间. 本文所获结果可为实际器件的研制提供理论支撑.In recent years, researchers have proposed a model of graphene thermionic energy converter (GTEC) for the utilization of high-grade thermal energy, which is used to extensively study the physical mechanism and parametric optimization. However, the influences of space charge accumulation and near-field radiative effects on the GTEC’s energy conversion performance are rarely reported. In the present work, the theories of thermionic emission, Langmuir space charge, non-equilibrium thermodynamics, and fluctuating electrodynamics are used to construct an improved model, in which the coupling effects of thermionic transport, near-field radiative heat transfer, and Newton heat transfer are considered. Firstly, the dependence of additional potential barrier, current density, power density, efficiency, and heat flows on the voltage and the vacuum gap are analyzed by neglecting the Newton heat transfer. The results show that the vacuum gap has a significant influence on the power density, while it has a negligible effect on the efficiency, the optimal power density and efficiency can be obtained at two different voltages. Secondly, the variations of power density and efficiency with voltage are analyzed on condition that the electrodes’ temperatures are restricted by the energy balance equation. It is found that Newton heat transfer has a significant influence on the power density, while it has a negligible effect on the conversion efficiency; the anode’s temperature at the optimal power density is higher than the ambient temperature, and the temperature at the optimal efficiency is close to the ambient temperature; the optimal regions of voltage, vacuum gap, and anode’s temperature are determined by considering the trade-off between power density and efficiency. The results obtained in this work can provide a theoretical basis for the development of practical devices.
-
Keywords:
- graphene /
- thermionic transport /
- near-field heat transport /
- work function /
- Langmuir space charge theory
[1] 吴限量, 张德贤, 蔡宏琨, 周严, 倪牮, 张建军 2015 64 096102
Google Scholar
Wu X, Zhang D, Cai H, Zhou Y, Ni J, Zhang J 2015 Acta Phys. Sin. 64 096102
Google Scholar
[2] 于海童, 刘东, 杨震, 段远源 2018 67 024209
Google Scholar
Yu H, Liu, Yang Z 2018 Acta Phys. Sin. 67 024209
Google Scholar
[3] 廖天军, 吕贻祥 2020 69 057202
Google Scholar
Liao T, Lü Y, 2020 Acta Phys. Sin. 69 057202
Google Scholar
[4] Elahi A N M T, Devon J, Mohammad G, Keunhan P 2021 Sol. Energy Mater. Sol. Cells 226 111067
Google Scholar
[5] Liao T, Chen X, Lin B, Chen J 2016 Appl. Phys. Lett. 108 033901
Google Scholar
[6] Chen L, Ding Z, Zhou J, Wang W, Sun F. 2017 Eur. Phys. J. Plus 132 293
Google Scholar
[7] Liao T 2019 IEEE Electron Device Lett. 40 115
Google Scholar
[8] Datas A, Martí A 2017 Sol. Energy Mater. Sol. Cells 161 285
Google Scholar
[9] Deng Y, Qiu B, Lu K, et al. 2020 Appl. Therm. Eng. 173 115237
Google Scholar
[10] Liao T, Dai Y, Cheng C, Dai Y, Cheng C, Ni M 2020 J. Power Sources 478 228797
Google Scholar
[11] Chen S, Zhang H, Wang F, He M, Zhao J, Zhang C, Yuan J 2021 Int. J. Hydrogen Energy 46 22062
Google Scholar
[12] Post A D, King B V, Kisi E H 2017 Appl. Therm. Eng. 117 245
Google Scholar
[13] Zhang X, Ang Y S, Du J Y, Chen J, Ang L K 2020 J. Clean. Prod. 242 118444
Google Scholar
[14] Liang S J, Ang L K 2015 Phys. Rev. Appl. 3 014002
[15] Misra S, Kahaly M U, Mishra S K 2017 J. Appl. Phys. 121 065102
Google Scholar
[16] Mishra S K, Kahaly M U, Misra S 2017 In. J. Thermal Sci. 121 358
Google Scholar
[17] Yang Z, Peng W, Li W, Chen X, Chen J 2018 J. Appl. Phys. 124 154501
Google Scholar
[18] 廖天军, 林比宏, 王宇珲 2019 68 187901
Google Scholar
Liao T, Lin B, Wang Y 2019 Acta Phys. Sin. 68 187901
Google Scholar
[19] Hu C, Liang T, Chen X, Chen J 2021 Appl. Phys. Lett. 118 083901
Google Scholar
[20] Freitag M, Chiu H Y, Steiner M, Perebeinos V, Avouris P 2010 Nature Nanotech. 5 497
Google Scholar
[21] Jensen D, Elahi A N M T, Ghashami M, Keunhan P 2021 Phys. Rev. Appl. 15 024062
Google Scholar
[22] Smith J R, Bibro G L, Nemanich R J 2007 Phys. Rev. B 76 245327
Google Scholar
[23] Liang S J, Liu B, Hu W, Zhou K, Ang L K 2017 Sci. Rep. 7 46211
Google Scholar
[24] 杜玮, 尹格, 马云贵 2020 69 204203
Google Scholar
Du W, Yin G, Ma Y 2020 Acta Phys. Sin. 69 204203
Google Scholar
[25] Messina R, Ben-Abdallah P 2013 Sci. Rep. 3 1383
Google Scholar
[26] Mikhailov S A, Ziegler K 2007 Phys. Rev. lett. 99 016803
Google Scholar
[27] Su S, Zhang H, Chen X, Kang J, Chen J 2013 Sol. Energy Mater. Sol. Cells 117 219
Google Scholar
[28] 廖天军, 陈渝, 杨智敏 2021 中国科学: 技术科学 51 46
Google Scholar
Liao T, Chen Y, Yang Z 2021 Sci. Sin. Tech. 51 46
Google Scholar
[29] Olawole O C, De D K 2018 J. Photon. Energy 8 018001
[30] Liao T, Lin J, Tao C, Lin B 2020 Renew. Energy 162 1715
Google Scholar
[31] 禹忠, 党忠, 柯熙政, 崔真 2016 65 248103
Google Scholar
Yu Z, Dang Z, Ke X, Cui Z 2016 Acta Phys. Sin. 65 248103
Google Scholar
[32] Jiang Y, Sun Y Y, Chen M, Wang Y, Li Z, Song C, He K, Wang L, Chen X, Xue Q, Ma X, Zhang S B 2012 Phys. Rev. Lett. 108 066809
Google Scholar
[33] Banhart F, Kotakoski J, Krasheninnikov A V 2011 ACS Nano 5 26
Google Scholar
[34] 杜一帅, 康维, 郑瑞伦 2017 66 014701
Google Scholar
Du Y, Kang W, Zheng R 2017 Acta Phys. Sin. 66 014701
Google Scholar
-
图 1 GTEC的结构和能带示意图 (a)结构; (b)能带
Fig. 1. The structure and band diagrams of the GTEC: (a) Structure; (b) band
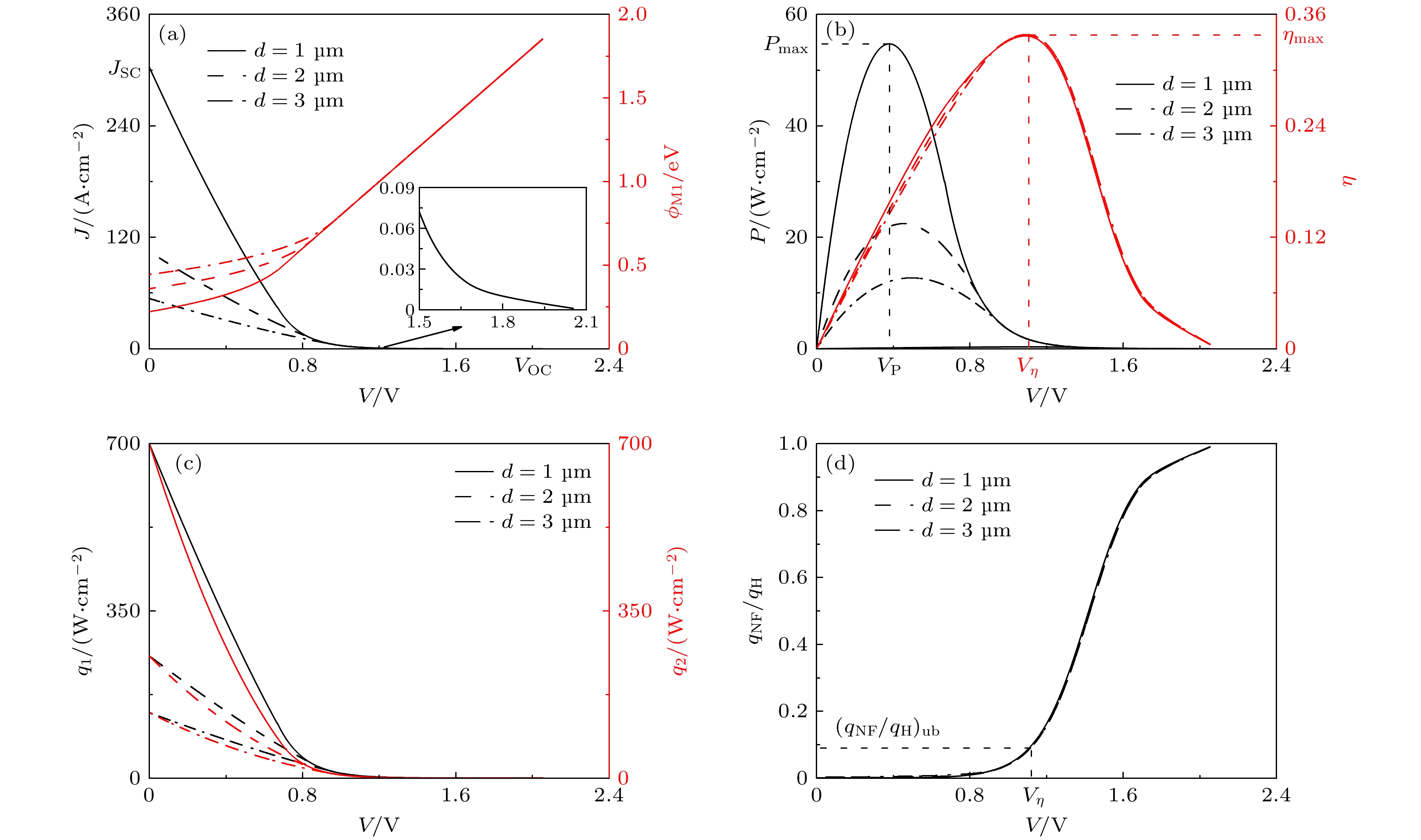
图 2 三个不同真空间隙条件下, GTEC的净电流密度
$ J $ 与阴极板势垒高度$ {\phi _{{\text{M1}}}} $ 、功率密度$ P $ 与转换效率$ \eta $ 、热流$ {q_1} $ 和$ {q_2} $ , 以及近场辐射热流与阴极板热流的比值$ {{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}} $ 随电压$ V $ 的变化关系曲线 (a)$ J $ 与$ {\phi _{{\text{M1}}}} $ ; (b)$ P $ 与$ \eta $ ; (c)$ {q_1} $ 和$ {q_2} $ ; (d)$ {{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}} $ Fig. 2. The curves net electrical current density
$ J $ and cathode’s additional barrier$ {\phi _{{\text{M1}}}} $ , power density$ P $ and efficiency$ \eta $ , heat flow rates$ {q_1} $ and$ {q_2} $ , and the ratio of$ {q_{{\text{NF}}}} $ to$ {q_{\text{H}}} $ varying with the voltage$ V $ for given three values of$ d $ : (a)$ J $ and$ {\phi _{{\text{M1}}}} $ ; (b)$ P $ and$ \eta $ ; (c)$ {q_1} $ and$ {q_2} $ ; (d)$ {{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}} $ .
图 3 极板温度
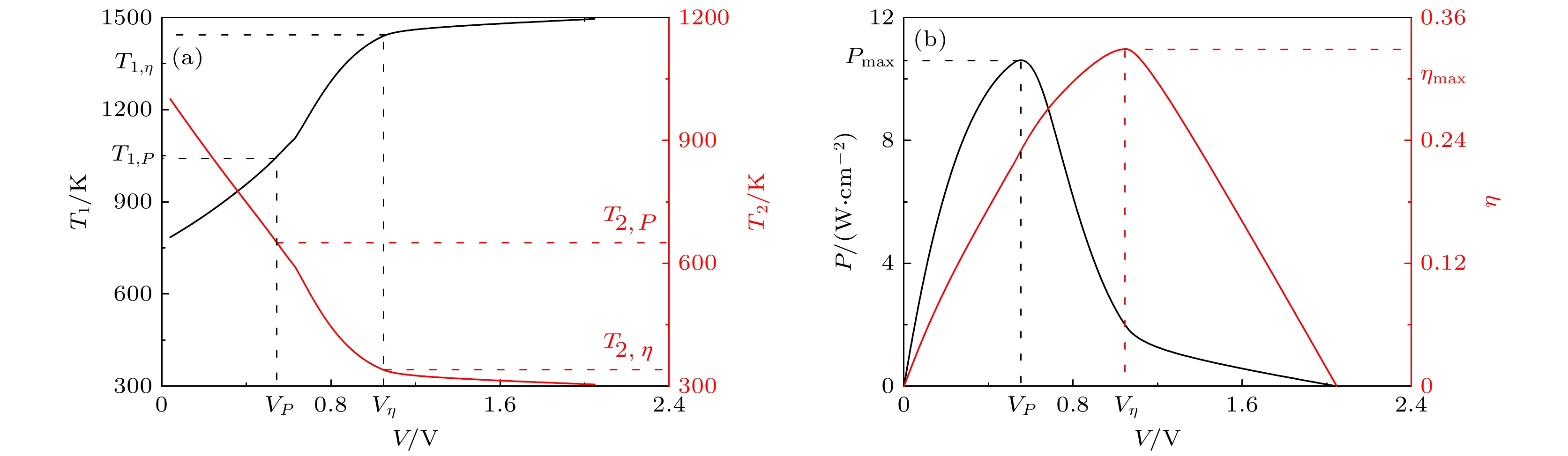
$ {T_1} $ 与$ {T_{\text{2}}} $ 和功率密度$ P $ 与效率$ \eta $ 随电压$ V $ 的变化曲线, 其中$d = 1.5\, {\text{μm}}$ (a)$ {T_1} $ 与$ {T_{\text{2}}} $ ; (b)$ P $ 与$ \eta $ Fig. 3. The curves cathode’s operating temperature
$ {T_1} $ and anode’s operating temperature$ {T_{\text{2}}} $ and power density$ P $ and efficiency$ \eta $ varying with the voltage$ V $ , where$d = 1.5\, {\text{μm}}$ : (a)$ {T_1} $ and$ {T_{\text{2}}} $ ; (b)$ P $ and$ \eta $ .
图 4 (a)最高功率密度
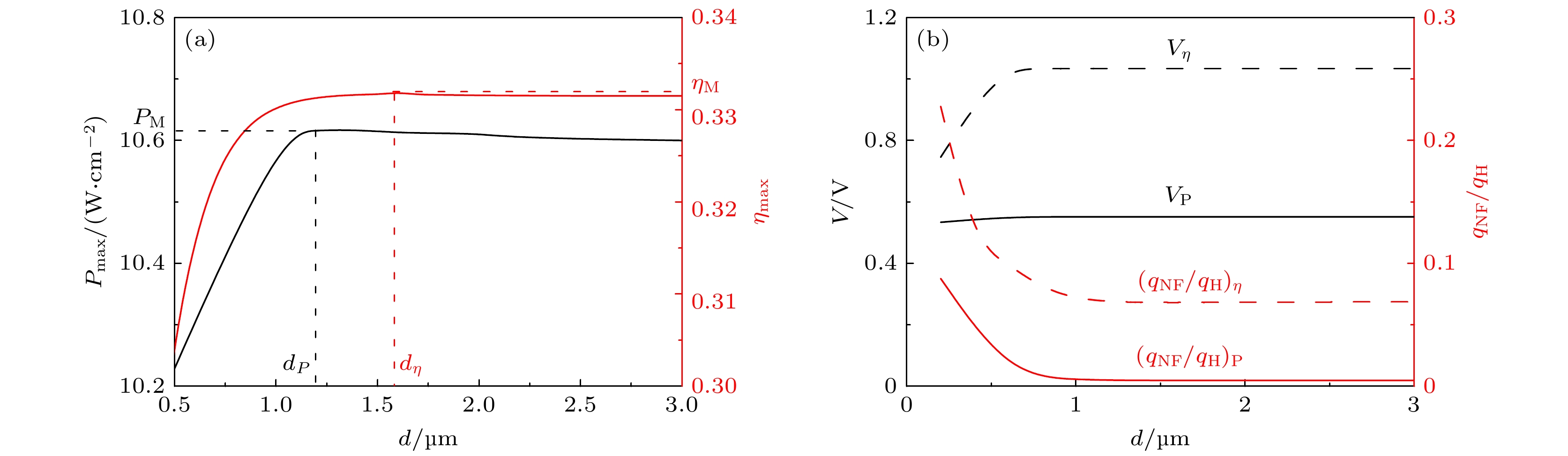
$ {P_{\max }} $ 与效率$ {\eta _{\max }} $ 和(b)优化电压$ {V_P} $ 和$ {V_\eta } $ 以及优化比值$ {\left( {{{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}}} \right)_P} $ 和$ {\left( {{{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}}} \right)_\eta } $ 随真空间隙$ d $ 的变化曲线Fig. 4. The curves (a) the maximum power density
$ {P_{\max }} $ and efficiency$ {\eta _{\max }} $ and (b) the optimum operating voltages$ {V_P} $ and$ {V_\eta } $ , and the optimum ratios$ {\left( {{{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}}} \right)_P} $ and$ {\left( {{{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}}} \right)_\eta } $ varying with the vacuum gap$ d $ . -
[1] 吴限量, 张德贤, 蔡宏琨, 周严, 倪牮, 张建军 2015 64 096102
Google Scholar
Wu X, Zhang D, Cai H, Zhou Y, Ni J, Zhang J 2015 Acta Phys. Sin. 64 096102
Google Scholar
[2] 于海童, 刘东, 杨震, 段远源 2018 67 024209
Google Scholar
Yu H, Liu, Yang Z 2018 Acta Phys. Sin. 67 024209
Google Scholar
[3] 廖天军, 吕贻祥 2020 69 057202
Google Scholar
Liao T, Lü Y, 2020 Acta Phys. Sin. 69 057202
Google Scholar
[4] Elahi A N M T, Devon J, Mohammad G, Keunhan P 2021 Sol. Energy Mater. Sol. Cells 226 111067
Google Scholar
[5] Liao T, Chen X, Lin B, Chen J 2016 Appl. Phys. Lett. 108 033901
Google Scholar
[6] Chen L, Ding Z, Zhou J, Wang W, Sun F. 2017 Eur. Phys. J. Plus 132 293
Google Scholar
[7] Liao T 2019 IEEE Electron Device Lett. 40 115
Google Scholar
[8] Datas A, Martí A 2017 Sol. Energy Mater. Sol. Cells 161 285
Google Scholar
[9] Deng Y, Qiu B, Lu K, et al. 2020 Appl. Therm. Eng. 173 115237
Google Scholar
[10] Liao T, Dai Y, Cheng C, Dai Y, Cheng C, Ni M 2020 J. Power Sources 478 228797
Google Scholar
[11] Chen S, Zhang H, Wang F, He M, Zhao J, Zhang C, Yuan J 2021 Int. J. Hydrogen Energy 46 22062
Google Scholar
[12] Post A D, King B V, Kisi E H 2017 Appl. Therm. Eng. 117 245
Google Scholar
[13] Zhang X, Ang Y S, Du J Y, Chen J, Ang L K 2020 J. Clean. Prod. 242 118444
Google Scholar
[14] Liang S J, Ang L K 2015 Phys. Rev. Appl. 3 014002
[15] Misra S, Kahaly M U, Mishra S K 2017 J. Appl. Phys. 121 065102
Google Scholar
[16] Mishra S K, Kahaly M U, Misra S 2017 In. J. Thermal Sci. 121 358
Google Scholar
[17] Yang Z, Peng W, Li W, Chen X, Chen J 2018 J. Appl. Phys. 124 154501
Google Scholar
[18] 廖天军, 林比宏, 王宇珲 2019 68 187901
Google Scholar
Liao T, Lin B, Wang Y 2019 Acta Phys. Sin. 68 187901
Google Scholar
[19] Hu C, Liang T, Chen X, Chen J 2021 Appl. Phys. Lett. 118 083901
Google Scholar
[20] Freitag M, Chiu H Y, Steiner M, Perebeinos V, Avouris P 2010 Nature Nanotech. 5 497
Google Scholar
[21] Jensen D, Elahi A N M T, Ghashami M, Keunhan P 2021 Phys. Rev. Appl. 15 024062
Google Scholar
[22] Smith J R, Bibro G L, Nemanich R J 2007 Phys. Rev. B 76 245327
Google Scholar
[23] Liang S J, Liu B, Hu W, Zhou K, Ang L K 2017 Sci. Rep. 7 46211
Google Scholar
[24] 杜玮, 尹格, 马云贵 2020 69 204203
Google Scholar
Du W, Yin G, Ma Y 2020 Acta Phys. Sin. 69 204203
Google Scholar
[25] Messina R, Ben-Abdallah P 2013 Sci. Rep. 3 1383
Google Scholar
[26] Mikhailov S A, Ziegler K 2007 Phys. Rev. lett. 99 016803
Google Scholar
[27] Su S, Zhang H, Chen X, Kang J, Chen J 2013 Sol. Energy Mater. Sol. Cells 117 219
Google Scholar
[28] 廖天军, 陈渝, 杨智敏 2021 中国科学: 技术科学 51 46
Google Scholar
Liao T, Chen Y, Yang Z 2021 Sci. Sin. Tech. 51 46
Google Scholar
[29] Olawole O C, De D K 2018 J. Photon. Energy 8 018001
[30] Liao T, Lin J, Tao C, Lin B 2020 Renew. Energy 162 1715
Google Scholar
[31] 禹忠, 党忠, 柯熙政, 崔真 2016 65 248103
Google Scholar
Yu Z, Dang Z, Ke X, Cui Z 2016 Acta Phys. Sin. 65 248103
Google Scholar
[32] Jiang Y, Sun Y Y, Chen M, Wang Y, Li Z, Song C, He K, Wang L, Chen X, Xue Q, Ma X, Zhang S B 2012 Phys. Rev. Lett. 108 066809
Google Scholar
[33] Banhart F, Kotakoski J, Krasheninnikov A V 2011 ACS Nano 5 26
Google Scholar
[34] 杜一帅, 康维, 郑瑞伦 2017 66 014701
Google Scholar
Du Y, Kang W, Zheng R 2017 Acta Phys. Sin. 66 014701
Google Scholar
下载:
计量
- 文章访问数: 4665
- PDF下载量: 93
- 被引次数: 0
