-
为寻找核态可能存在的三轴形变, 用对力-形变-转动频率自洽推转壳模型对锗和硒同位素进行了总转动能面计算. 计算是在四极形变(β2, γ)网格中进行的, 且十六极形变β4可变. 在锗同位素中发现了由64Ge的三轴、66Ge的扁椭、再经三轴、向长椭形变的形状相变. 一般来说Ge和Se同位素具有γ软性形状, 导致了显著的动力学三轴效应, 计算中没有证据表明存在基态下的刚性三轴性. 在64,74Ge中发现基态和集体转动态下
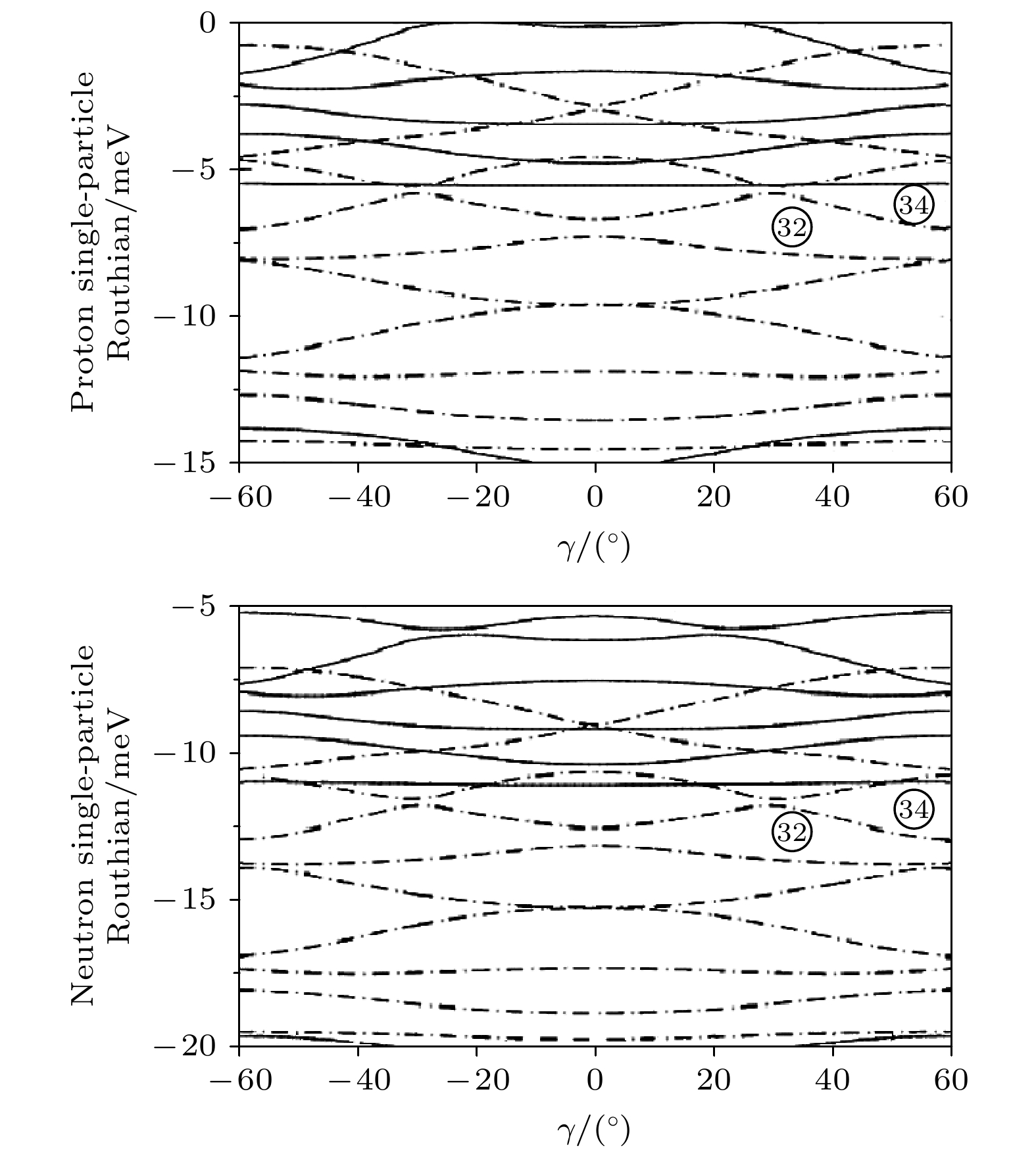
$ \gamma = - 30^\circ $ 的三轴形变, 这是三轴形变的极限. 本文重点讨论N = Z核64Ge可能存在的三轴形变, 给出了基于唯象Woods-Saxon势下的单粒子能级信息, 并对N = Z核64Ge三轴形变的产生机理进行了讨论.Evidence for nonaxial γ deformations has been widely found in collective rotational states. The γ deformation has led to very interesting characteristics of nuclear motions, such as wobbling, chiral band, and signature inversion in rotational states. There is an interesting question; why the nonaxial γ deformation is not favored in the ground states of even-even (e-e) nuclei. The quest for stable triaxial shapes in the ground states of e-e nuclei, with a maximum triaxial deformation of$ \left| \gamma \right| $ ≈ 30°, is still a major theme in nuclear structure. In the present work, we use the cranked Woods-Saxon (WS) shell model to investigate possible triaxial shapes in ground and collective rotational states. Total-Routhian-surface calculations by means of the pairing-deformation-frequency self-consistent cranked shell model are carried out for even-even germanium and selenium isotopes, in order to search for possible triaxial deformations of nuclear states. Calculations are performed in the lattice of quadrupole (β2, γ) deformations with the hexadecapole β4 variation. In fact, at each grid point of the quadrupole deformation (β2, γ) lattice, the calculated energy is minimized with respect to the hexadecapole deformation β4. The shape phase transition from triaxial shape in 64Ge, oblate shape in 66Ge, again through triaxiality, to prolate deformations is found in germanium isotopes. In general, the Ge and Se isotopes have γ-soft shapes, resulting in significant dynamical triaxial effect. There is no evidence in the calculations pointing toward rigid triaxiality in ground states. The triaxiality of$ \gamma = - 30^\circ $ for the ground and collective rotational states, that is the limit of triaxial shape, is found in 64, 74Ge. One should also note that the depth of the triaxial minimum increases with rotational frequency increasing in these two nuclei. The present work focuses on the possible triaxial deformation of N = Z nucleus 64Ge. Single-particle level diagrams can give a further understanding of the origin of the triaxiality. Based on the information about single-particle levels obtained with the phenomenological Woods-Saxon (WS) potential, the mechanism of triaxial deformation in N = Z nucleus 64Ge is discussed, and caused surely by a deformed γ≈30° shell gap at Z(N) = 32. At N = 34, however, an oblate shell gap appears, which results in an oblate shape in 66Ge (N = 34). With neutron number increasing, the effect from the N = 34 oblate gap decreases, and hence the deformations of heavier Ge isotopes change toward the triaxiality (or prolate).-
Keywords:
- triaxial deformation /
- total Routhian surface /
- shape evaluation
[1] Tajima N, Suzuki N 2001 Phys. Rev. C 64 037301
Google Scholar
[2] Nazarewicz W 1993 Phys. Lett. B 305 195
Google Scholar
[3] Bohr A, Mottelson B R 1975 Nuclear Structure (Vol. II) (New York: Benjamin)
[4] Frauendorf S, Meng J 1997 Nucl. Phys. A 617 131
Google Scholar
[5] Bengtsson R, Frisk H, May F R, Pinston J A 1984 Nucl. Phys. A 415 189
Google Scholar
[6] Narimatsu K, Shimizu Y R, Shizuma T 1996 Nucl. Phys. A 601 69
Google Scholar
[7] Guo L, Maruhn J A, Reinhard P-G 2007 Phys. Rev. C 76 034317
Google Scholar
[8] Ødegård S W, Hagemann G B, Jensen D R, Bergström M, Herskind B, Sletten G, Törmänen S, Wilson J N, Tjøm P O, Hamamoto I, Spohr K, Hübel H, Görgen A, Schönwasser G, Bracco A, Leoni S, Maj A, Petrache C M, Bednarczyk P, Curien D 2001 Phys. Rev. Lett. 86 5866
Google Scholar
[9] Schönwaßer G, Hübel H, Hagemann G B, Bednarczyk P, Benzoni G, Bracco A, Bringel P, Chapman R, Curien D, Domscheit J, Herskind B, Jensen D R, Leoni S, Bianco G Lo, Ma W C, Maj A, Neußer A, Ødegård S W, Petrache C M, Roßbach D, Ryde H, Spohr K H, Singh A K 2003 Phys. Lett. B 552 9
Google Scholar
[10] Hartley D J, Janssens R V F, Riedinger L L, Riley M A, Aguilar A, Carpenter M P, Chiara C J, Chowdhury P, Darby I G, Garg U, Ijaz Q A, Kondev F G, Lakshmi S, Lauritsen T, Ludington A, Ma W C, McCutchan E A, Mukhopadhyay S, Pifer R, Seyfried E P, Stefanescu I, Tandel S K, Tandel U, Vanhoy J R, Wang X, Zhu S, Hamamoto I, Frauendorf S 2009 Phys. Rev. C 80 041304
Google Scholar
[11] Ennis P J, Lister C J, Gelletly W, Price H G, Varley B J, Butler P A, Hoare T, Ćwiok S, Nazarewicz W 1991 Nucl. Phys. A 535 392
Google Scholar
[12] Yamagami M, Matsuyanagi K, Matsuo M 2001 Nucl. Phys. A 693 579
Google Scholar
[13] Skalski J 1991 Phys. Rev. C 43 140
Google Scholar
[14] Bonche P, Flocard H, Heenen P H 1991 private communication
[15] Kaneko K, Hasegawa M, Mizusaki T 2002 Phys. Rev. C 66 051306
Google Scholar
[16] Andrejtscheff W, Petkov P 1994 Phys. Lett. B 329 1
Google Scholar
[17] Cline D 1986 Annu. Rev. Nucl. Part. Sci. 36 683
Google Scholar
[18] Kumar K 1972 Phys. Rev. Lett. 28 249
Google Scholar
[19] Andrejtscheff W, Petkov P 1993 Phys. Rev. C 48 2531
Google Scholar
[20] Hamamoto I 1990 Nucl. Phys. A 520 297c
Google Scholar
[21] Åberg I, Flocard H, Nazarewicz W 1990 Annu. Rev. Nucl. Part. Sci. 40 439
Google Scholar
[22] Zamfir N V, Casten R F 1991 Phys. Lett. B 260 265
Google Scholar
[23] Satuła W, Wyss R, Magierski P 1994 Nucl. Phys. A 578 45
Google Scholar
[24] Satuła W, Wyss R 1995 Phys. Scr. T 56 159
Google Scholar
[25] Nazarewicz W, Dudek J, Bengtsson R, Bengtsson T, Ragnarsson I 1985 Nucl. Phys. A 435 397
Google Scholar
[26] Ćwiok S, Dudek J, Nazarewicz W, Skalski S, Werner T 1987 Comput. Phys. Commun. 46 379
Google Scholar
[27] Bhagwat A, Vinas X, Centelles M, Schuck P, Wyss R 2010 Phys. Rev. C 81 044321
Google Scholar
[28] Meng H Y, Hao Y W, Wang H L, Liu M L 2018 Prog. Theor. Exp. Phys. 2018 103D02
Google Scholar
[29] Pradhan H C, Nogami Y, Law J 1973 Nucl. Phys. A 201 357
Google Scholar
[30] Nazarewicz W, Riley M A, Garrett J D 1990 Nucl. Phys. A 512 61
Google Scholar
[31] Möller P, Nix J R 1992 Nucl. Phys. A 536 20
Google Scholar
[32] Myers W D, Swiatecki W J 1966 Nucl. Phys. 81 1
Google Scholar
[33] Strutinsky V M 1966 Yad. Fiz. 3 614
[34] Strutinsky V M 1967 Nucl. Phys. A 95 420
Google Scholar
[35] Sakamoto H, Kishimoto T 1990 Phys. Lett. B 245 321
Google Scholar
[36] Satuła W, Wyss R 1994 Phys. Rev. C 50 2888
Google Scholar
[37] Granderath A, Mantica P F, Bengtsson R, Wyss R, Brentano P von, Gelberg A, Seiffert F 1996 Nucl. Phys. A 597 427
Google Scholar
[38] Lecomte R, Irshad M, Landsberger S, Kajrys G, Paradis P, Monaro S 1980 Phys. Rev. C 22 2420
Google Scholar
[39] Ward D, Fallon P 2001 Adv. Nucl. Phys. 26 167
[40] Xu F R, Walker P M, Wyss R 2002 Phys. Rev. C 65 021303
Google Scholar
[41] Farhan A R 1995 Nucl. Data Sheets 74 529
Google Scholar
[42] Toh Y, Czosnyka T, Oshima M, Hayakawa T, Kusakari H, Sugawara M, Hatsukawa Y, Katakura J, Shinohara N, Matsuda M 2000 Eur. Phys. J. A 9 353
Google Scholar
[43] Werner V, Scholl C, Brentano P von 2005 Eur. Phys. J. A 25 s01 453
Google Scholar
-
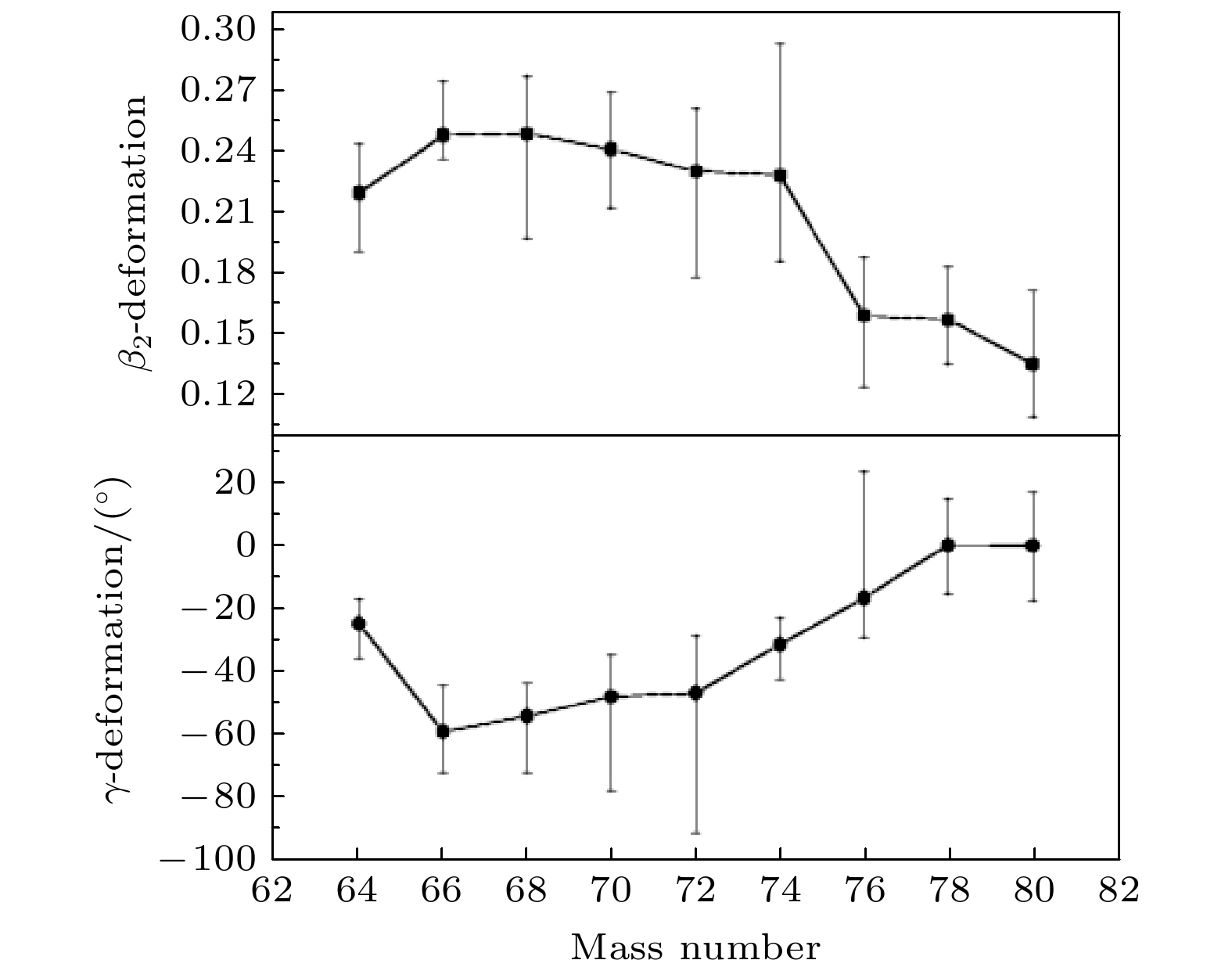
图 1 总转动能面计算得出的偶质量核64-80Ge的基态形变. 误差棒显示对应于能量高出最小值100 keV以内的形变值, 此表示各个核对应于相应形变参数(
$ {\beta _2} $ 和$ \gamma $ )的软度Fig. 1. Deformation obtained from total Routhian surfaces for ground states in even-mass 64-80Ge. The error bars display the deformation values within an energy range of less than 100 keV above the minimum, giving an indication of the softness of the nucleus with respect to the corresponding shape parameter(
$ {\beta _2} $ and$ \gamma $ ).
图 2 对64Ge的正宇称转晕态在给定转动频率 (a)
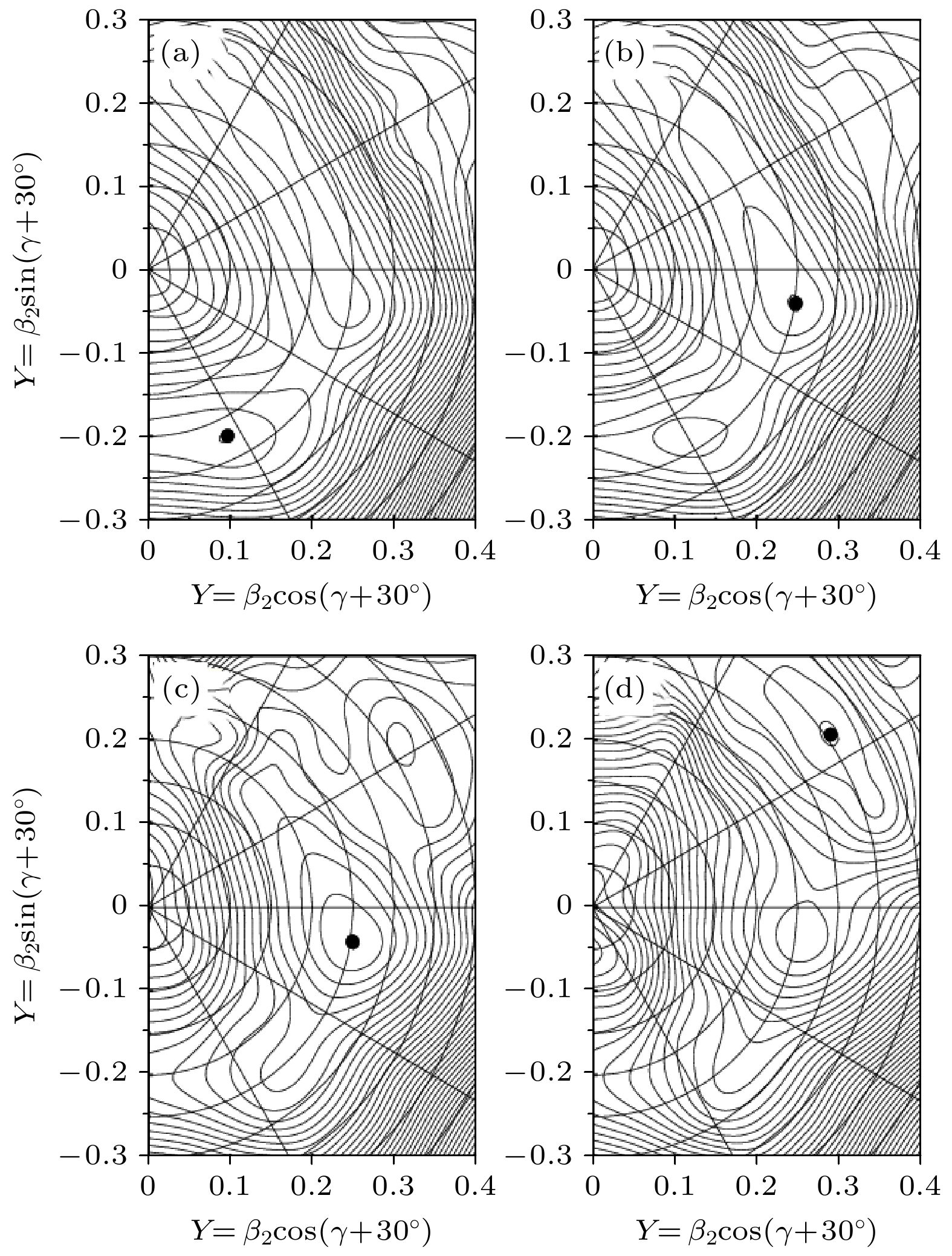
$ \hbar \omega $ = 0.0 MeV, (b)$ \hbar \omega $ = 0.4 MeV, (c)$ \hbar \omega $ = 0.7 MeV和(d)$ \hbar \omega $ = 0.9 MeV下计算得到的总转动能面, 其对应于自旋$I \sim (0 - $ $ 16)\hbar$ . 图中黑点表示最小值, 相邻等位线的间隔是200 keVFig. 2. Calculated TRS's for 64Ge positive-parity yrast states at (a)
$ \hbar \omega $ = 0.0 MeV, (b) 0.4 MeV, (c) 0.7 MeV, and (d) 0.9 MeV corresponding to$ I \sim (0 - 16)\hbar $ . The black dot indicates the lowest minimum, and the energy difference between neighboring contours is 200 keV.
图 3 对应于三轴形变参数γ的Woods-Saxon势单粒子能级图
Fig. 3. The calculated Woods-Saxon single-particle levels versus the triaxial deformation γ.
图 4 对(a) 74Ge和(b) 74Se核由TRS计算得到的运动学转动惯量J(1)与由实验结果提取出的比较
Fig. 4. The kinematic moment of inertia J(1) calculated by TRS is compared with those extracted from the experimental results for (a) 74Ge and (b) 74Se.
-
[1] Tajima N, Suzuki N 2001 Phys. Rev. C 64 037301
Google Scholar
[2] Nazarewicz W 1993 Phys. Lett. B 305 195
Google Scholar
[3] Bohr A, Mottelson B R 1975 Nuclear Structure (Vol. II) (New York: Benjamin)
[4] Frauendorf S, Meng J 1997 Nucl. Phys. A 617 131
Google Scholar
[5] Bengtsson R, Frisk H, May F R, Pinston J A 1984 Nucl. Phys. A 415 189
Google Scholar
[6] Narimatsu K, Shimizu Y R, Shizuma T 1996 Nucl. Phys. A 601 69
Google Scholar
[7] Guo L, Maruhn J A, Reinhard P-G 2007 Phys. Rev. C 76 034317
Google Scholar
[8] Ødegård S W, Hagemann G B, Jensen D R, Bergström M, Herskind B, Sletten G, Törmänen S, Wilson J N, Tjøm P O, Hamamoto I, Spohr K, Hübel H, Görgen A, Schönwasser G, Bracco A, Leoni S, Maj A, Petrache C M, Bednarczyk P, Curien D 2001 Phys. Rev. Lett. 86 5866
Google Scholar
[9] Schönwaßer G, Hübel H, Hagemann G B, Bednarczyk P, Benzoni G, Bracco A, Bringel P, Chapman R, Curien D, Domscheit J, Herskind B, Jensen D R, Leoni S, Bianco G Lo, Ma W C, Maj A, Neußer A, Ødegård S W, Petrache C M, Roßbach D, Ryde H, Spohr K H, Singh A K 2003 Phys. Lett. B 552 9
Google Scholar
[10] Hartley D J, Janssens R V F, Riedinger L L, Riley M A, Aguilar A, Carpenter M P, Chiara C J, Chowdhury P, Darby I G, Garg U, Ijaz Q A, Kondev F G, Lakshmi S, Lauritsen T, Ludington A, Ma W C, McCutchan E A, Mukhopadhyay S, Pifer R, Seyfried E P, Stefanescu I, Tandel S K, Tandel U, Vanhoy J R, Wang X, Zhu S, Hamamoto I, Frauendorf S 2009 Phys. Rev. C 80 041304
Google Scholar
[11] Ennis P J, Lister C J, Gelletly W, Price H G, Varley B J, Butler P A, Hoare T, Ćwiok S, Nazarewicz W 1991 Nucl. Phys. A 535 392
Google Scholar
[12] Yamagami M, Matsuyanagi K, Matsuo M 2001 Nucl. Phys. A 693 579
Google Scholar
[13] Skalski J 1991 Phys. Rev. C 43 140
Google Scholar
[14] Bonche P, Flocard H, Heenen P H 1991 private communication
[15] Kaneko K, Hasegawa M, Mizusaki T 2002 Phys. Rev. C 66 051306
Google Scholar
[16] Andrejtscheff W, Petkov P 1994 Phys. Lett. B 329 1
Google Scholar
[17] Cline D 1986 Annu. Rev. Nucl. Part. Sci. 36 683
Google Scholar
[18] Kumar K 1972 Phys. Rev. Lett. 28 249
Google Scholar
[19] Andrejtscheff W, Petkov P 1993 Phys. Rev. C 48 2531
Google Scholar
[20] Hamamoto I 1990 Nucl. Phys. A 520 297c
Google Scholar
[21] Åberg I, Flocard H, Nazarewicz W 1990 Annu. Rev. Nucl. Part. Sci. 40 439
Google Scholar
[22] Zamfir N V, Casten R F 1991 Phys. Lett. B 260 265
Google Scholar
[23] Satuła W, Wyss R, Magierski P 1994 Nucl. Phys. A 578 45
Google Scholar
[24] Satuła W, Wyss R 1995 Phys. Scr. T 56 159
Google Scholar
[25] Nazarewicz W, Dudek J, Bengtsson R, Bengtsson T, Ragnarsson I 1985 Nucl. Phys. A 435 397
Google Scholar
[26] Ćwiok S, Dudek J, Nazarewicz W, Skalski S, Werner T 1987 Comput. Phys. Commun. 46 379
Google Scholar
[27] Bhagwat A, Vinas X, Centelles M, Schuck P, Wyss R 2010 Phys. Rev. C 81 044321
Google Scholar
[28] Meng H Y, Hao Y W, Wang H L, Liu M L 2018 Prog. Theor. Exp. Phys. 2018 103D02
Google Scholar
[29] Pradhan H C, Nogami Y, Law J 1973 Nucl. Phys. A 201 357
Google Scholar
[30] Nazarewicz W, Riley M A, Garrett J D 1990 Nucl. Phys. A 512 61
Google Scholar
[31] Möller P, Nix J R 1992 Nucl. Phys. A 536 20
Google Scholar
[32] Myers W D, Swiatecki W J 1966 Nucl. Phys. 81 1
Google Scholar
[33] Strutinsky V M 1966 Yad. Fiz. 3 614
[34] Strutinsky V M 1967 Nucl. Phys. A 95 420
Google Scholar
[35] Sakamoto H, Kishimoto T 1990 Phys. Lett. B 245 321
Google Scholar
[36] Satuła W, Wyss R 1994 Phys. Rev. C 50 2888
Google Scholar
[37] Granderath A, Mantica P F, Bengtsson R, Wyss R, Brentano P von, Gelberg A, Seiffert F 1996 Nucl. Phys. A 597 427
Google Scholar
[38] Lecomte R, Irshad M, Landsberger S, Kajrys G, Paradis P, Monaro S 1980 Phys. Rev. C 22 2420
Google Scholar
[39] Ward D, Fallon P 2001 Adv. Nucl. Phys. 26 167
[40] Xu F R, Walker P M, Wyss R 2002 Phys. Rev. C 65 021303
Google Scholar
[41] Farhan A R 1995 Nucl. Data Sheets 74 529
Google Scholar
[42] Toh Y, Czosnyka T, Oshima M, Hayakawa T, Kusakari H, Sugawara M, Hatsukawa Y, Katakura J, Shinohara N, Matsuda M 2000 Eur. Phys. J. A 9 353
Google Scholar
[43] Werner V, Scholl C, Brentano P von 2005 Eur. Phys. J. A 25 s01 453
Google Scholar
下载:
计量
- 文章访问数: 4119
- PDF下载量: 81
- 被引次数: 0
