-
在大脑皮层中, 神经元大范围的同步放电可以引发癫痫, 而癫痫发作期间可以自发出现螺旋波, 大量神经元的同步放电与螺旋波自发产生之间的关系目前仍不清楚. 本文通过增加水平长程连接构造了具有局域长程耦合区的二维神经元网络, 采用Morris-Lecar神经元模型研究了具有多个长方形长程耦合区的神经元网络中波的传播, 数值模拟结果表明: 传播方向与长程耦合朝向平行的平面波和靶波经过长程耦合区会导致长程耦合区内的神经元同步激发, 这种同步激发伴随一部分神经元延迟激发, 而另一部分提前激发; 当长程耦合区宽度超过临界宽度时, 长程耦合区所有神经元延迟激发; 当长程耦合区宽度超过最大导通宽度时, 波将不能通过长程耦合区. 当适当选择长方形长程耦合区的尺寸时, 神经元同步激发可使网络出现波回传效应和具有波传播方向的选择性, 而且这种波传播方向的选择性对神经元是否处于定态和耦合强度变化很敏感, 以致高频平面波列可以部分通过宽度超过最大导通宽度的长程耦合区, 因此可以通过对长程耦合区内的神经元施加微扰来控制低频波是否可以通过一定宽度的长程耦合区. 对于适当选取的神经元网络结构, 当平面波或靶波经过长程耦合区时, 网络可自发出现自维持平面波、螺旋波和靶波等现象. 本文对产生这些现象的物理机制作了分析.In the cerebral cortex, the large-scale synchronous firing of neurons can cause epilepsy, during which spiral waves can spontaneously occur. The relationship between the synchronous firing of a large number of neurons and the spontaneous generation of spiral waves is still unclear. In this paper, a two-dimensional neuronal network with the long-range coupling regions generated by adding long-range horizontal connections is constructed. The Morris-Lecar neuron model is used to study the propagation of waves in the two-dimensional neuronal network with the rectangular long-range coupling regions. Numerical simulation results show that the plan and target waves whose propagation directions are both parallel to that of the long-range coupling can lead the neurons to be excited synchronously in the long-range coupling region. This synchronous firing is accompanied by delayed firing of some neurons and premature firing of others. When the width of the long-range coupling region exceeds the critical width, all the neurons in the long-range coupling region delay firing. When the width of the long-range coupling region exceeds a maximum conduction width, the waves will not pass through the long-range coupling region. When the size of the rectangular region of the long-range coupling is selected appropriately, the synchronous excitation of neurons can cause network to present the backfiring effect and to have the selectivity of wave propagation direction. Furthermore, the selectivity of wave propagation direction is very sensitive to whether the neuron is in the stationary state and also to the change of coupling strength, so that the high frequency plane wave train can partially pass through the long-range coupling region whose width exceeds the maximum conduction width. So we can control whether the wave can pass through the long-range coupling region of a certain width by giving the neurons in the long-range coupling region a tiny perturbation. When one or two long-range coupling regions are constructed in the neural network and the size of the long-range coupling regions is selected appropriately, the self-sustaining plane wave, spiral wave and target wave can appear spontaneously in the network when the wave passes through the long-range coupling regions. The physical mechanisms behind those phenomena are also analyzed.
-
Keywords:
- synchronization /
- spiral wave /
- long-range coupling
[1] Ouyang Q, Flesselles J M 1996 Nature 379 143
Google Scholar
[2] Ecke R E, Hu Y C, Mainieri R, Ahlers G 1995 Science 269 1704
Google Scholar
[3] Davidenko J M, Pertsov A V, Salomonsz R, Baxter W, Jalife J 1992 Nature 355 349
Google Scholar
[4] Chen X W, Li P F, Yuan X P, Zhao Y H, Ma J, Chen J X 2019 Commun. Theor. Phys. 71 334
Google Scholar
[5] Zimik S, Pandit R 2017 Sci. Rep. 7 15350
Google Scholar
[6] Huang X Y, Xu W F, Liang J M, Takagaki K, Gao X, Wu J Y 2010 Neuron 68 978
Google Scholar
[7] Huang X Y, Troy W C, Yang Q, Ma H T, Laing C R, Schiff S J, Wu J Y 2004 J. Neurosci. 24 9897
Google Scholar
[8] Sato T K, Nauhaus I, Carandini M 2012 Neuron 75 218
Google Scholar
[9] Stacey W 2012 Epilepsy Curr. 12 147
Google Scholar
[10] Isomura Y, Fujiwara-Tsukamoto Y, Takada M 2008 Neurosci. Res. 61 227
Google Scholar
[11] Yu Y F, Santos L M, Mattiace L A, et al. 2012 Proc. Natl. Acad. Sci. USA 109 2585
Google Scholar
[12] Jung P, Cornell-Bell A, Madden K S, Moss F 1998 J. Neurophysiol. 79 1098
Google Scholar
[13] Qin H X, Ma J, Wang C N, Chu R T 2014 Sci. China Phys. Mech. 57 1918
Google Scholar
[14] 汪芃, 李倩昀, 黄志精, 唐国宁 2018 67 170501
Google Scholar
Wang P, Li Q Y, Huang Z J, Tang G N 2018 Acta Phys. Sin. 67 170501
Google Scholar
[15] 黄志精, 李倩昀, 白婧, 唐国宁 2019 68 110503
Google Scholar
Huang Z J, Li Q Y, Bai J, Tang G N 2019 Acta Phys. Sin. 68 110503
Google Scholar
[16] Gunji A, Ishii R, Chau W, Kakigi R, Pantev C 2007 NeuroImage 34 426
Google Scholar
[17] Baptista M S, Szmoski R M, Pereira R F, Pinto S E D S 2016 Sci. Rep. 6 22617
Google Scholar
[18] Antonopoulos C G, Srivastava S, Pinto S E D S, Baptista M S 2015 Plos Comput. Biol. 11 e1004372
Google Scholar
[19] Wang Q Y, Lu Q S 2005 Chin. Phys. Lett. 22 543
Google Scholar
[20] Yanchuk S, Perlikowski P, Popovych O V, Tass P A 2011 Chaos 21 047511
Google Scholar
[21] Belykh I, Lange E D, Hasler M 2005 Phys. Rev. Lett. 94 188101
Google Scholar
[22] 孙晓娟, 杨白桦, 吴晔, 肖井华 2014 63 180507
Google Scholar
Sun X J, Yang B H, Wu Y, Xiao J H 2014 Acta Phys. Sin. 63 180507
Google Scholar
[23] Shi X, Wang Q Y, Lu Q S 2008 Cogn. Neurodyn. 2 195
Google Scholar
[24] Manjarrez E, Rojas-Piloni J G, Mendez I, Martinez L, Velez D, Vazquez D, Flores A 2002 Neurosci. Lett. 326 93
Google Scholar
[25] Glatt E, Busch H, Kaiser F, Zaikin A 2006 Phys. Rev. E 73 026216
Google Scholar
[26] 孙晓娟, 李国芳 2016 65 120502
Google Scholar
Sun X J, Li G F 2016 Acta Phys. Sin. 65 120502
Google Scholar
[27] Gan C B, Matjaz P, Wang Q Y 2010 Chin. Phys. B 19 040508
Google Scholar
[28] Yu H T, Guo X M, Wang J 2017 Commun. Nonlinear Sci. Numer. Simulat. 42 532
Google Scholar
[29] Wang Q Y, Zhang H H, Chen G R 2012 Chaos 22 043123
Google Scholar
[30] Wu Y, Liu D, Song Z 2015 Neuroscience 287 175
Google Scholar
[31] Morris C, Lecar H 1981 Biophys. J. 35 193
Google Scholar
[32] Tang Z, Li Y Y, Xi L, Jia B, Gu H G 2012 Commun. Theor. Phys. 57 61
Google Scholar
-
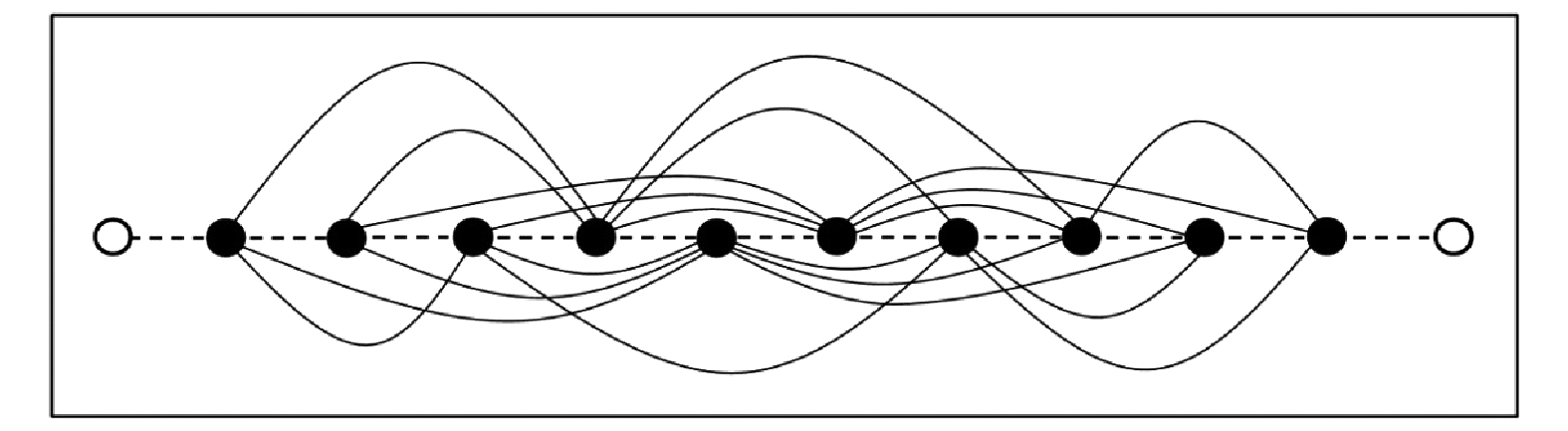
图 1 神经元之间的长程耦合示意图, 虚线代表近邻耦合, 实线代表长程耦合, 空心圆代表长程耦合区外的神经元, 实心圆代表长程耦合区内的神经元
Fig. 1. Schematic diagram of long-range coupling between neurons. Dashed and solid lines represent the nearest neighbor and long-range coupling, respectively. Hollow and solid circles represent the neurons outside and inside the long-range coupling region, respectively.
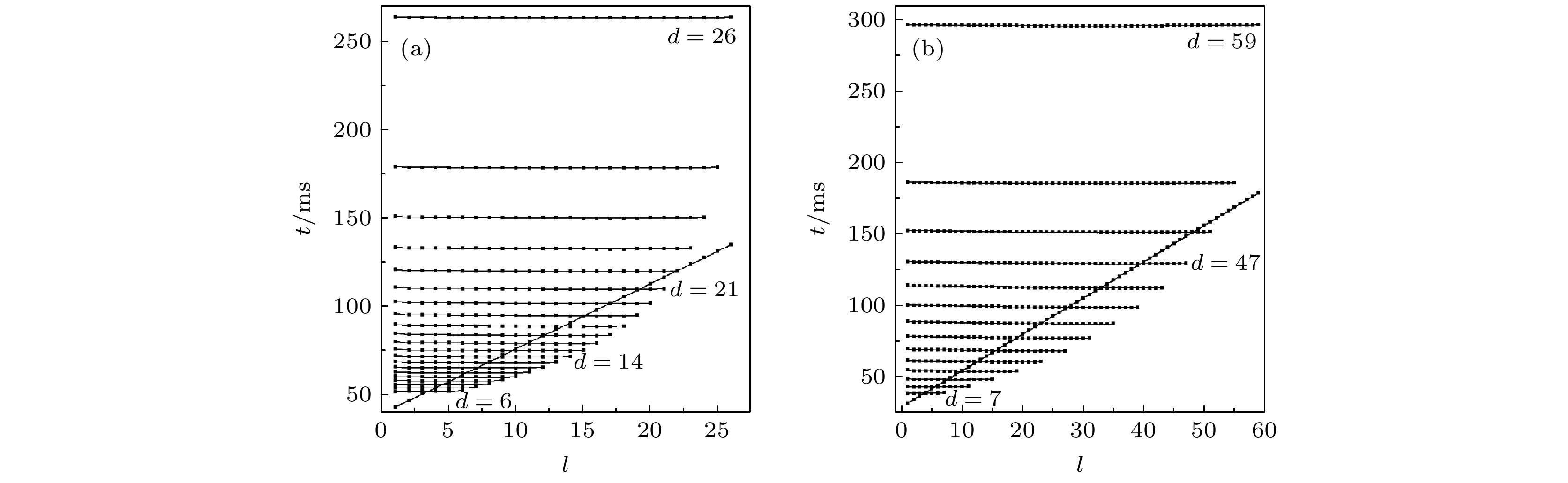
图 2 不同耦合强度和不同宽度下神经元激发时刻随位置
$ l $ 的变化, 斜线对应无长程耦合情况, 不同水平线上的黑点个数对应不同宽度的长程耦合区 (a)$ \varepsilon {\text{ = }}0.2 $ ; (b)$ \varepsilon {\text{ = }}0.4 $ Fig. 2. The firing time point of neurons varies with location
$ l $ for different coupling strengths and different widths of the long-range coupling region. The oblique line corresponds to the network without long-range coupling, and the number of black dots on different horizontal lines is the width of the corresponding coupling region: (a)$ \varepsilon {\text{ = }}0.2 $ ; (b)$ \varepsilon {\text{ = }}0.4 $ .
图 3 在
$ \varepsilon {\text{ = }}0.2 $ 的情况下不同时刻的膜电位斑图, 白色虚线矩形框内为长程耦合区, 其宽度$ d = 50 $ . 上下两排图的波传播方向分别与长程耦合方向平行和垂直 (a), (d)$ t = 74{\text{ ms}} $ ; (b), (e)$ t = 228{\text{ ms}} $ ; (c), (f)$ t = 556{\text{ ms}} $ Fig. 3. Membrane-potential patterns at different time points for
$ \varepsilon {\text{ = }}0.2 $ . The box marked by a white dotted rectangle shows the long-range coupling region, and its width is equal to 50. The wave propagation directions in the upper and lower row panels are parallel and perpendicular to the long-range coupling direction, respectively: (a), (d)$ t = 74{\text{ ms}} $ ; (b), (e)$ t = 228{\text{ ms}} $ ; (c), (f)$t = $ $ 556{\text{ ms}}$ .
图 4 在
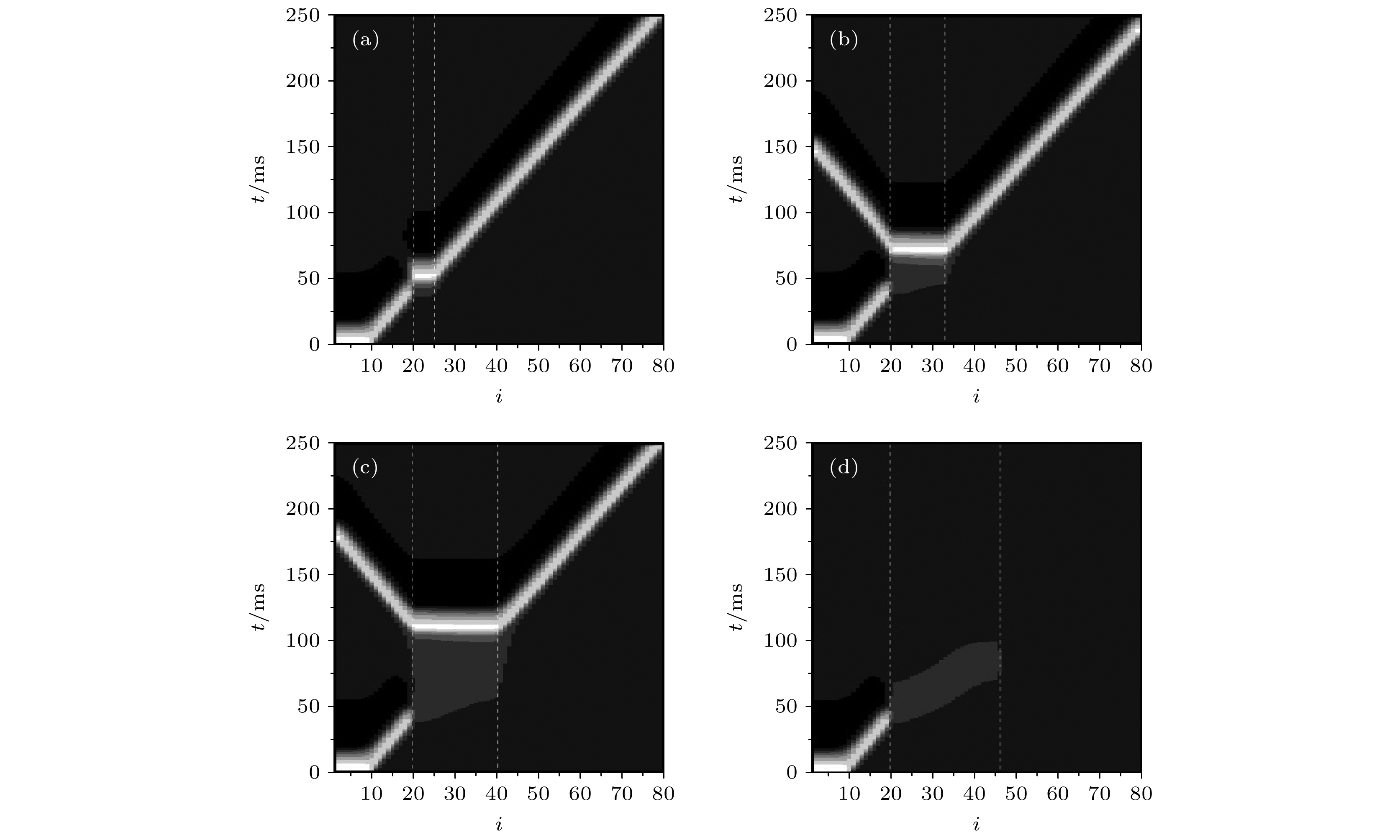
$ \varepsilon {\text{ = }}0.2 $ 和不同的长程耦合区宽度的情况下一行格点的膜电位的时空斑图, 两白色虚线之间的区域为长程耦合区 (a)$d = $ $ 6$ ; (b)$ d = 14 $ ; (c)$ d = 21 $ ; (d)$ d = 27 $ Fig. 4. Spatiotemporal patterns of membrane potential of a row of grid points for
$ \varepsilon {\text{ = }}0.2 $ and different widths of long-range coupling region. The region between the two white dotted lines is the long-range coupling region: (a)$ d = 6 $ ; (b)$ d = 14 $ ; (c)$ d = 21 $ ; (d)$ d = 27 $ .
图 5 在
$ d{\text{ = }}27 $ ,$ \varepsilon {\text{ = }}0.2 $ 和不同周期T平面波下神经元的激发时刻随位置$ l $ 的变化. 空心圆对应无长程耦合结果, 实心方块对应有长程耦合的结果 (a)$ T{\text{ = }}300{\text{ ms}} $ ; (b)$ T{\text{ = }}450{\text{ ms}} $ ; (c)$ T{\text{ = }}480{\text{ ms}} $ Fig. 5. The firing time point of neurons varies with location
$ l $ for$ d{\text{ = }}27 $ ,$ \varepsilon {\text{ = }}0.2 $ and different periods of planar wave. The hollow circles show the results obtained without long-range coupling, while the solid squares show the results obtained with long-range coupling: (a)$ T{\text{ = }}300{\text{ ms}} $ ; (b)$ T{\text{ = }}450{\text{ ms}} $ ; (c)$ T{\text{ = }}480{\text{ ms}} $ .
图 6 在
$ L{\text{ = }}N $ ,$ d = 14 $ 和Δ = 13的情况下不同时刻的膜电位斑图, 左边(右边)两条白色虚线之间为长程耦合区 (a)$ t = $ $ 150{\text{ ms}} $ ; (b)$ t = 292{\text{ ms}} $ ; (c)$ t = 342{\text{ ms}} $ ; (d)$ t = 370{\text{ ms}} $ ; (e)$ t = 428{\text{ ms}} $ ; (f)$ t = 478{\text{ ms}} $ ; (g)$ t = 528{\text{ ms}} $ ; (h)$ t = 570{\text{ ms}} $ .Fig. 6. Patterns of the membrane potential at different time points for
$ L{\text{ = }}N $ ,$ d = 14 $ and Δ = 13. The region between two white dotted lines on the left (right) is the long-range coupling region: (a)$ t = 150{\text{ ms}} $ ; (b)$ t = 292{\text{ ms}} $ ; (c)$ t = 342{\text{ ms}} $ ; (d)$ t = 370{\text{ ms}} $ ; (e)$ t = 428{\text{ ms}} $ ; (f)$ t = 478{\text{ ms}} $ ; (g)$ t = 528{\text{ ms}} $ ; (h)$ t = 570{\text{ ms}} $ .
图 7 在
$ L = 35 $ ,$ d = 14 $ , Δ = 1的情况下不同时刻的膜电位斑图, 两个白色虚线框内为长程耦合区 (a)$ t = 150{\text{ ms}} $ ; (b)$ t = 306{\text{ ms}} $ ; (c)$ t = 318{\text{ ms}} $ ; (d)$ t = 346{\text{ ms}} $ ; (e)$ t = 442{\text{ ms}} $ ; (f)$ t = 490{\text{ ms}} $ ; (g)$ t = 514{\text{ ms}} $ ; (h)$ t = 816{\text{ ms}} $ Fig. 7. Patterns of the membrane potential at different time points for
$ L{\text{ = }}35 $ ,$ d = 14 $ and Δ = 1. The two boxes marked by white dotted rectangle show the long-range coupling regions: (a)$ t = 150{\text{ ms}} $ ; (b)$ t = 306{\text{ ms}} $ ; (c)$ t = 318{\text{ ms}} $ ; (d)$ t = 346{\text{ ms}} $ ; (e)$ t = 442{\text{ ms}} $ ; (f)$ t = 490{\text{ ms}} $ ; (g)$ t = 514{\text{ ms}} $ ; (h)$t = 816{\text{ ms}}$ 
图 8 在
$ d = 14 $ , Δ = 13和不同L下不同时刻的膜电位斑图, 两个白色虚线框内为长程耦合区. 三个长程耦合区的长度分别为$ L = 61, {\text{ }}101, {\text{ }}161 $ (a)$ t = 1308\;{\text{ ms}} $ ; (b)$ t = 2890\;{\text{ ms}} $ ; (c)$ t = 3718\;{\text{ ms}} $ ; (d)$ t = 1370\;{\text{ ms}} $ ; (e)$ t = 2690\;{\text{ ms}} $ ; (f)$ t = 3710\;{\text{ ms}} $ ; (g)$ t = 1296\;{\text{ ms}} $ ; (h)$ t = 2400\;{\text{ ms}} $ ; (i)$ t = 3750\;{\text{ ms}} $ Fig. 8. Patterns of the membrane potential at different time points for
$ d = 14 $ , Δ = 13 and different L. The two boxes marked by white dotted rectangle show the long-range coupling regions. The lengths of the three long-range coupling regions are equal to 60, 101, 161, respectively: (a)$ t = 1308\;{\text{ ms}} $ ; (b)$ t = 2890\;{\text{ ms}} $ ; (c)$ t = 3718\;{\text{ ms}} $ ; (d)$ t = 1370\;{\text{ ms}} $ ; (e)$ t = 2690\;{\text{ ms}} $ ; (f)$ t = 3710\;{\text{ ms}} $ ;(g)$ t = 1296\;{\text{ ms}} $ ; (h)$ t = 2400\;{\text{ ms}} $ ; (i)$ t = 3750\;{\text{ ms}} $ .
图 9 在
$ \varepsilon {\text{ = }}0.2 $ ,$ L = 41 $ 和$ d = 21 $ 的情况下不同时刻的膜电位斑图. 白色虚线框内为长程耦合区 (a)$ t = 292\;{\text{ ms}} $ ; (b)$t = $ $ 320\;{\text{ ms}}$ ; (c)$ t = 348\;{\text{ ms}} $ ; (d)$ t = 640\;{\text{ ms}} $ ; (e)$ t = 758\;{\text{ ms}} $ ; (f)$ t = 854\;{\text{ ms}} $ ; (g)$ t = 890\;{\text{ ms}} $ ; (h)$ t = 932\;{\text{ ms}} $ Fig. 9. Patterns of the membrane potential at different time points for
$ \varepsilon {\text{ = }}0.2 $ ,$ L = 41 $ and$ d = 21 $ . The box marked by white dotted rectangle shows the long-range coupling region: (a)$ t = 292{\text{ ms}} $ ; (b)$ t = 320\;{\text{ ms}} $ ; (c)$ t = 348\;{\text{ ms}} $ ; (d)$ t = 640\;{\text{ ms}} $ ; (e)$t = $ $ 758\;{\text{ ms}}$ ; (f)$ t = 854\;{\text{ ms}} $ ; (g)$ t = 890\;{\text{ ms}} $ ; (h)$ t = 932\;{\text{ ms}} $ .
图 10 某时刻膜电位斑图, 白色虚线框内为长程耦合区. 第一排图(第二排图)使用靶波源
${{\rm{S}}_1}$ (${{\rm{S}}_2}$ ), 箭头所指为靶波源位置 (a)$t = $ $ 760\;{\text{ ms}}$ ; (b)$ t = 858\;{\text{ ms}} $ ; (c)$ t = 1082\;{\text{ ms}} $ ; (d)$ t = 1992\;{\text{ ms}} $ ; (e)$ t = 1862\;{\text{ ms}} $ ; (f)$ t = 1390\;{\text{ ms}} $ Fig. 10. Membrane potential patterns at a certain time point. The box marked by white dotted rectangle shows the long-range coupling region. The first row (second row) panel use the target wave source
${{\rm{S}}_1}$ (${{\rm{S}}_2}$ ). The arrow indicates the location of the target wave source: (a)$ t = 760\;{\text{ ms}} $ ; (b)$ t = 858\;{\text{ ms}} $ ; (c)$ t = 1082\;{\text{ ms}} $ ; (d)$ t = 1992\;{\text{ ms}} $ ; (e)$ t = 1862\;{\text{ ms}} $ ; (f)$ t = 1390\;{\text{ ms}} $ . -
[1] Ouyang Q, Flesselles J M 1996 Nature 379 143
Google Scholar
[2] Ecke R E, Hu Y C, Mainieri R, Ahlers G 1995 Science 269 1704
Google Scholar
[3] Davidenko J M, Pertsov A V, Salomonsz R, Baxter W, Jalife J 1992 Nature 355 349
Google Scholar
[4] Chen X W, Li P F, Yuan X P, Zhao Y H, Ma J, Chen J X 2019 Commun. Theor. Phys. 71 334
Google Scholar
[5] Zimik S, Pandit R 2017 Sci. Rep. 7 15350
Google Scholar
[6] Huang X Y, Xu W F, Liang J M, Takagaki K, Gao X, Wu J Y 2010 Neuron 68 978
Google Scholar
[7] Huang X Y, Troy W C, Yang Q, Ma H T, Laing C R, Schiff S J, Wu J Y 2004 J. Neurosci. 24 9897
Google Scholar
[8] Sato T K, Nauhaus I, Carandini M 2012 Neuron 75 218
Google Scholar
[9] Stacey W 2012 Epilepsy Curr. 12 147
Google Scholar
[10] Isomura Y, Fujiwara-Tsukamoto Y, Takada M 2008 Neurosci. Res. 61 227
Google Scholar
[11] Yu Y F, Santos L M, Mattiace L A, et al. 2012 Proc. Natl. Acad. Sci. USA 109 2585
Google Scholar
[12] Jung P, Cornell-Bell A, Madden K S, Moss F 1998 J. Neurophysiol. 79 1098
Google Scholar
[13] Qin H X, Ma J, Wang C N, Chu R T 2014 Sci. China Phys. Mech. 57 1918
Google Scholar
[14] 汪芃, 李倩昀, 黄志精, 唐国宁 2018 67 170501
Google Scholar
Wang P, Li Q Y, Huang Z J, Tang G N 2018 Acta Phys. Sin. 67 170501
Google Scholar
[15] 黄志精, 李倩昀, 白婧, 唐国宁 2019 68 110503
Google Scholar
Huang Z J, Li Q Y, Bai J, Tang G N 2019 Acta Phys. Sin. 68 110503
Google Scholar
[16] Gunji A, Ishii R, Chau W, Kakigi R, Pantev C 2007 NeuroImage 34 426
Google Scholar
[17] Baptista M S, Szmoski R M, Pereira R F, Pinto S E D S 2016 Sci. Rep. 6 22617
Google Scholar
[18] Antonopoulos C G, Srivastava S, Pinto S E D S, Baptista M S 2015 Plos Comput. Biol. 11 e1004372
Google Scholar
[19] Wang Q Y, Lu Q S 2005 Chin. Phys. Lett. 22 543
Google Scholar
[20] Yanchuk S, Perlikowski P, Popovych O V, Tass P A 2011 Chaos 21 047511
Google Scholar
[21] Belykh I, Lange E D, Hasler M 2005 Phys. Rev. Lett. 94 188101
Google Scholar
[22] 孙晓娟, 杨白桦, 吴晔, 肖井华 2014 63 180507
Google Scholar
Sun X J, Yang B H, Wu Y, Xiao J H 2014 Acta Phys. Sin. 63 180507
Google Scholar
[23] Shi X, Wang Q Y, Lu Q S 2008 Cogn. Neurodyn. 2 195
Google Scholar
[24] Manjarrez E, Rojas-Piloni J G, Mendez I, Martinez L, Velez D, Vazquez D, Flores A 2002 Neurosci. Lett. 326 93
Google Scholar
[25] Glatt E, Busch H, Kaiser F, Zaikin A 2006 Phys. Rev. E 73 026216
Google Scholar
[26] 孙晓娟, 李国芳 2016 65 120502
Google Scholar
Sun X J, Li G F 2016 Acta Phys. Sin. 65 120502
Google Scholar
[27] Gan C B, Matjaz P, Wang Q Y 2010 Chin. Phys. B 19 040508
Google Scholar
[28] Yu H T, Guo X M, Wang J 2017 Commun. Nonlinear Sci. Numer. Simulat. 42 532
Google Scholar
[29] Wang Q Y, Zhang H H, Chen G R 2012 Chaos 22 043123
Google Scholar
[30] Wu Y, Liu D, Song Z 2015 Neuroscience 287 175
Google Scholar
[31] Morris C, Lecar H 1981 Biophys. J. 35 193
Google Scholar
[32] Tang Z, Li Y Y, Xi L, Jia B, Gu H G 2012 Commun. Theor. Phys. 57 61
Google Scholar
下载:
计量
- 文章访问数: 4839
- PDF下载量: 86
- 被引次数: 0
