-
纳米复合电极是提高中低温固体氧化物燃料电池(solid oxide fuel cell, SOFC)性能的新型前沿技术, 其内部三相界面(three phase boundary, TPB)处空间电荷层(space charge layer, SCL)效应凸显, 显著影响氧空位传输能力, 是其性能优异的重要原因之一. 现有研究广泛采用Poisson-Boltzmann方程模拟SCL效应, 受限于载流子电化学平衡假设(导体净电流为零), 难以准确地揭示SOFC运行条件下(净电流不为零) SCL效应的影响规律. 针对SOFC模式电极, 本文耦合Poisson方程与载流子质量守恒方程, 建立了运行条件下考虑SCL效应的氧空位传输数理模型及数值模拟方法. 模拟研究表明, SCL效应导致TPB附近产生明显的氧空位浓度梯度, 从而产生显著的扩散电流, 其数值甚至高于电势梯度驱动的迁移电流. 采用SCL电阻表征SCL效应对氧空位传输过程的影响, 发现随着无量纲Debye长度与无量纲电势的增大, SCL电阻呈现减小的变化趋势; 增大无量纲平均电流密度, SCL电阻逐渐增大. 本文研究工作可为通过科学设计纳米复合电极以提高中低温SOFC性能提供理论依据.The nanocomposite electrode is a promising technology to improve the electrochemical performance of intermediate/low temperature solid oxide fuel cells (SOFCs). Within the nanocomposite electrode, the space charge layer (SCL) effect is likely to alternate the oxygen vacancy transport adjacent to the three phase boundaries (TPBs), which is one of the key factors to improve the electrochemical performance of the electrodes. Existing studies usually adopt Poisson-Boltzmann (PB) equation to predict the SCL effect, in which all the charge carriers are assumed to be in the electrochemical equilibrium state and the net current of the conductor is nearly zero. Apparently, the PB equation is incapable of predicting the SCL effects under typical SOFC operating conditions, since the net current is obviously not zero. In this paper, based on the patterned electrode, we develop a numerical method via coupling the Poisson equation with the mass conservation equation of charge carriers for the oxygen vacancy transport with considering the SCL effect under SOFC operating conditions. Our results show that an obvious gradient is observed in the oxygen vacancy concentration near the TPBs due to the SCL effect, which leads to a remarkable diffusion current that is even larger than the migration current driven by the potential gradient. The SCL resistance is computed to quantitatively characterize the influence of the SCL effect on the oxygen vacancy transport. The SCL resistance shows a decreasing tendency with the increasing of the dimensionless Debye length and dimensionless potential, but it increases with the increasing of the dimensionless average current density. These results and the numerical method can be helpful in improving the performance of intermediate/low temperature SOFCs via rationally designing robust nanocomposite electrodes.
-
Keywords:
- solid oxide fuel cell /
- space charge layer /
- oxygen vacancy transport /
- three phase boundary
[1] Wachsman E D, Lee K T 2011 Science 334 935
Google Scholar
[2] Gao Z, Mogni L V, Miller E C, Railsback J G, Barnett S A 2016 Energy Environ. Sci. 9 1602
Google Scholar
[3] Tong X, Mebane D S, De Souza R A 2020 J. Am. Ceram. Soc. 103 5
Google Scholar
[4] Zhao C, Li Y, Zhang W, Zheng Y, Lou X, Yu B, Chen J, Chen Y, Liu M, Wang J 2020 Energy Environ. Sci. 13 53
Google Scholar
[5] Lynch M E, Yang L, Qin W, Choi J, Liu M, Blinn K, Liu M 2011 Energy Environ. Sci. 4 2249
Google Scholar
[6] Zheng Y, Zhao C H, Li Y F, Zhang W Q, Wu T, Wang Z C, Li Z P, Chen J, Wang J C, Yu B, Zhang J J 2020 Nano Energy 78 105236
Google Scholar
[7] Uthayakumar A, Pandiyan A, Mathiyalagan S, Keshri A K, Moorthy S B K 2020 J. Phys. Chem. C 124 5591
Google Scholar
[8] Uthayakumar A, Pandiyan A, Krishna Moorthy S B 2018 Int. J. Hydrogen Energy 43 23488
Google Scholar
[9] Shirpour M, Merkle R, Lin C T, Maier J 2012 Phys. Chem. Chem. Phys. 14 730
Google Scholar
[10] Iguchi F, Chen C, Yugami H, Kim S 2011 J. Mater. Chem. 21 16517
Google Scholar
[11] Preethi S, Babu K S 2019 J. Alloys Compd. 792 1068
Google Scholar
[12] Kim S 2016 Phys. Chem. Chem. Phys. 18 19787
Google Scholar
[13] Kim S, Kim S K, Khodorov S, Maier J, Lubomirsky I 2016 Phys. Chem. Chem. Phys. 18 3023
Google Scholar
[14] Guan L L, Le S R, He S F, Zhu X D, Liu T, Sun K N 2015 Electrochim. Acta 161 129
Google Scholar
[15] Kim S K, Khodorov S, Chen C, Kim S, Lubomirsky I 2013 Phys. Chem. Chem. Phys. 15 8716
Google Scholar
[16] Kim S, Jain P, Avila-Paredes H J, Thron A, Benthem K V, SEN S 2010 J. Mater. Chem. 20 3855
Google Scholar
[17] Mebane D S, De Souza R A 2015 Energy Environ. Sci. 8 2935
Google Scholar
[18] Wang M, Kang Q 2010 J. Comput. Phys. 229 728
Google Scholar
[19] 徐晗, 张璐 2021 70 068801
Xu H, Zhang L 2021 Acta Phys. Sin. 70 068801
[20] Gregori G, Merkle R, Maier J 2017 Prog. Mater Sci. 89 252
Google Scholar
[21] Xu H, Chen Y, Kim J H, Dang Z, Liu M L 2019 Int. J. Hydrogen Energy 44 30293
Google Scholar
[22] 徐晗, 张璐, 党政 2020 69 098801
Google Scholar
Xu H, Zhang L, Dang Z 2020 Acta Phys. Sin. 69 098801
Google Scholar
[23] Xu H, Dang Z 2017 Int. J. Heat Mass Transfer 109 1252
Google Scholar
[24] Dang Z, Xu H 2016 Energy 107 295
Google Scholar
[25] Guo Z Z, Zheng C G, Shi B C 2002 Chin. Phys. 11 366
Google Scholar
[26] Connor P A, Yue X, Savaniu C D, Price R, Triantafyllou G, Cassidy M, Kerherve G, Payne D J, Maher R C, Cohen L F, Tomov R I, Glowacki B A, Kumar R V, Irvine J T S 2018 Adv. Energy Mater. 8 1800120
Google Scholar
[27] Chen Y, Chen Y, Ding D, Ding Y, Choi Y M, Zhang L, Yoo S, Chen D, deGlee B, Xu H, Lu Q, Zhao B, Vardar G, Wang J, Bluhme H, Crumline E J, Yang C, Liu J, Yildiz B, Liu M 2017 Energy Environ. Sci. 10 964
Google Scholar
[28] Zhang Y, Liu J, Singh M, Hu E, Jiang Z, Raza R, Wang F, Wang J, Yang F, Zhu B 2020 Nano-Micro Lett. 12 178
Google Scholar
[29] Zhu B 2009 Int. J. Energy Res. 33 1126
Google Scholar
[30] Zhu B, Li S, Mellander B E 2008 Electrochem. Commun. 10 302
Google Scholar
[31] 郭向欣, 李泓 2011 物理 40 648
Guo X, Li H 2011 Physics 40 648
[32] Crumlin E J, Mutoro E, Ahn S, La O G J, Leonard D N, Borisevich A, Biegalski M D, Christen H M, Shao-Horn Y 2010 J. Phys. Chem. Lett. 1 3149
Google Scholar
[33] 工藤徹一, 笛木和雄 (董治长 译) 1992 固态离子学 (北京: 北京工业大学出版社) 第35页
Kudo T, Fueki K (translated by Dong Z C) 1992 Solid Ionics (Beijing: Beijing University of Technology Press) p35 (in Chinese)
-
图 1 (a) SOFC模式电极几何结构示意图; (b), (c), (d)本文计算区域, 包括TPB附近的SCL与体相(Bulk)区域
Fig. 1. (a) Schematic of a patterned SOFC electrode; (b), (c), (d) computational domain considered in the present study, including the SCL and bulk area adjacent to the TPB.
图 3 本文LB模型验证: 右边界(x/l0 = 1)与上边界(y/l0 = 1)电势分布
Fig. 3. Validation of the present LB model: Potential distributions at the right (x/l0 = 1) and top (y/l0 = 1) boundary.
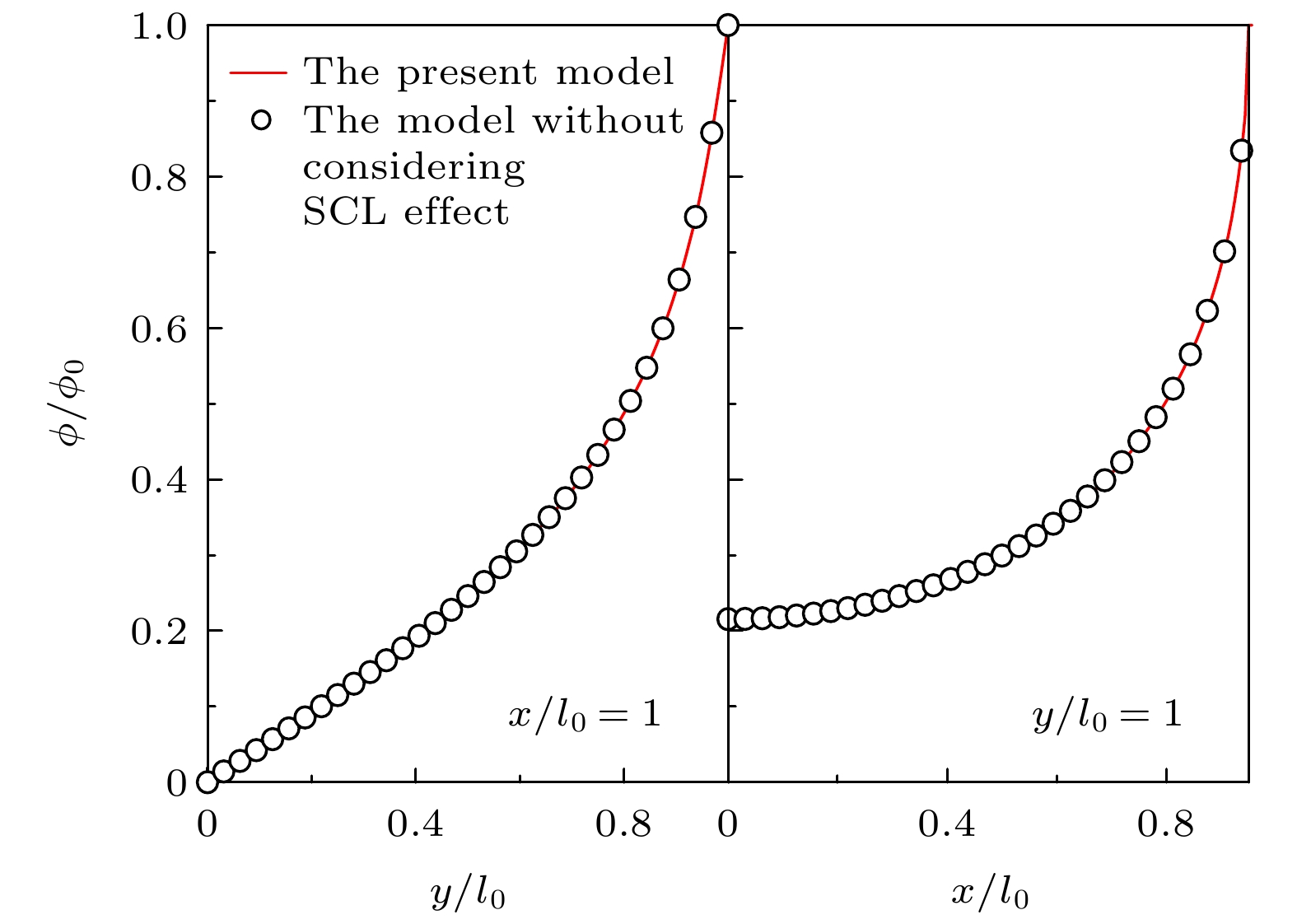
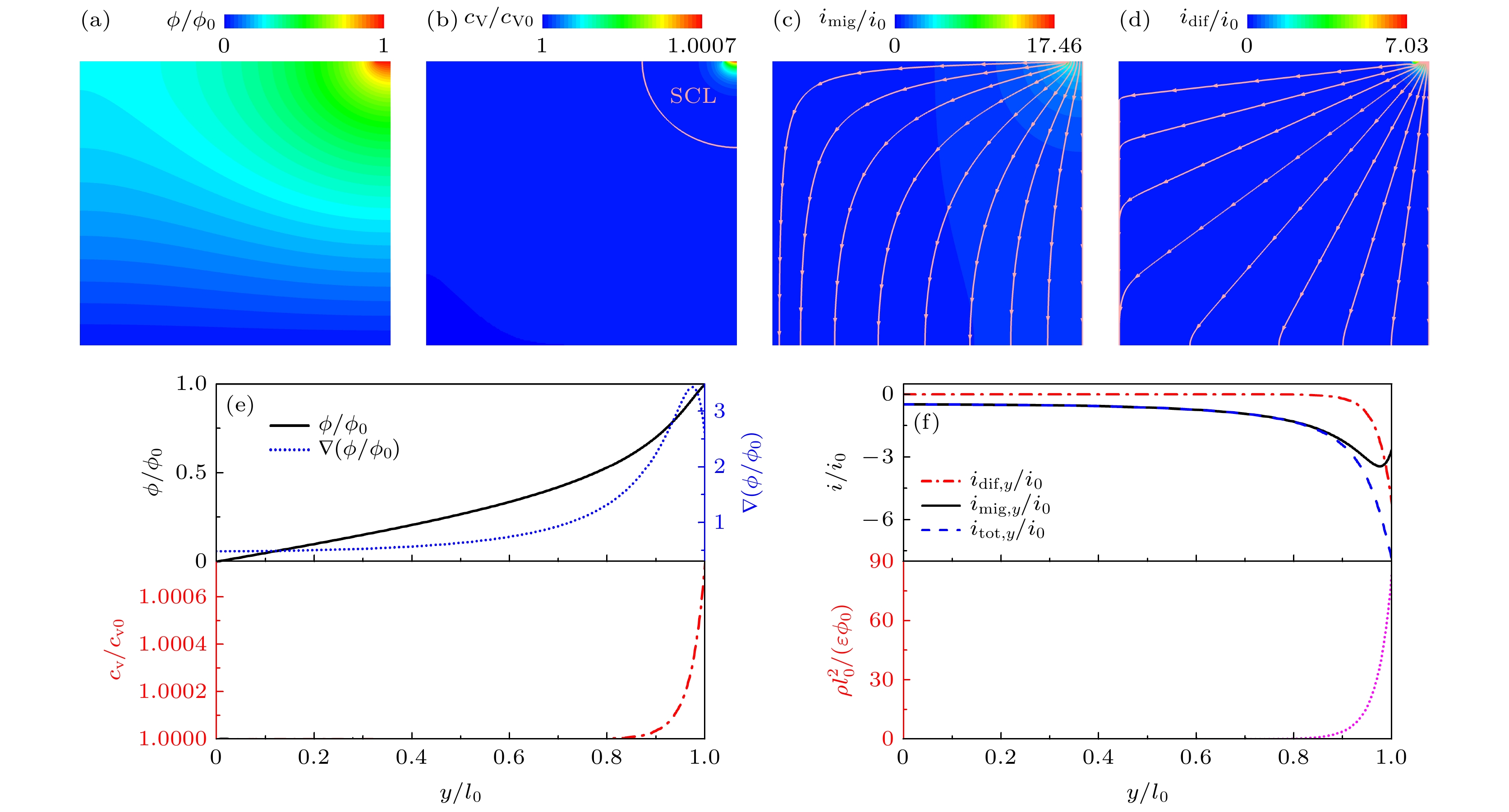
图 4 基准工况下TPB附近氧空位传输特性, 其中, 电势(a)与氧空位浓度(b)分布; 迁移(c)与扩散(d)电流密度大小及流线分布; 右边界(x/l0 = 1)电势、电势梯度与氧空位浓度(e), 以及电流密度与电荷密度分布(f)
Fig. 4. Oxygen vacancy transport adjacent to the TPB under standard case: Potential (a) and oxygen vacancy concentration (b) distribution; migration (c) and diffusion (d) current density streamline; distributions of potential, potential gradient, oxygen vacancy concentration (e), current density and charge density (f) at x/l0 = 1.
图 5 不同无量纲平均电流密度(iav/i0)下SCL效应的影响, 其中, 不同iav/i0下SCL电阻与TPB中心点氧空位浓度(a)、以及SCL厚度(b)分布; 当iav/i0分别为–1.6, –1, 1, 1.6, 以及x/l0 = 1时的界面电势(c)、氧空穴浓度(d)、迁移(e)与扩散(f)电流密度分布
Fig. 5. Influences of SCL effect under different dimensionless average current densities (iav/i0): The SCL resistance, oxygen vacancy concentration at central TPB (a), and SCL thickness (b) under different iav/i0; distributions of potential (c), oxygen vacancy concentration (d), migration (e) and diffusion (f) current density when iav/i0 = –1.6, –1, 1 and 1.6 at x/l0 = 1.
图 6 不同无量纲Debye长度(λD/l0)下SCL效应的影响, 其中, 不同λD/l0下SCL电阻与TPB中心点氧空位浓度(a)、以及SCL厚度(b)分布; 当λD/l0分别为0.005, 0.01, 0.05, 以及x/l0 = 1时的界面电势(c)、氧空穴浓度(d)、迁移(e)与扩散(f)电流密度分布
Fig. 6. Influences of SCL effect under different dimensionless Debye length (λD/l0): The SCL resistance, oxygen vacancy concentration at central TPB (a), and SCL thickness (b) under different λD/l0; distributions of potential (c), oxygen vacancy concentration (d), migration (e) and diffusion (f) current density when λD/l0 = 0.005, 0.01 and 0.05 at x/l0 = 1.
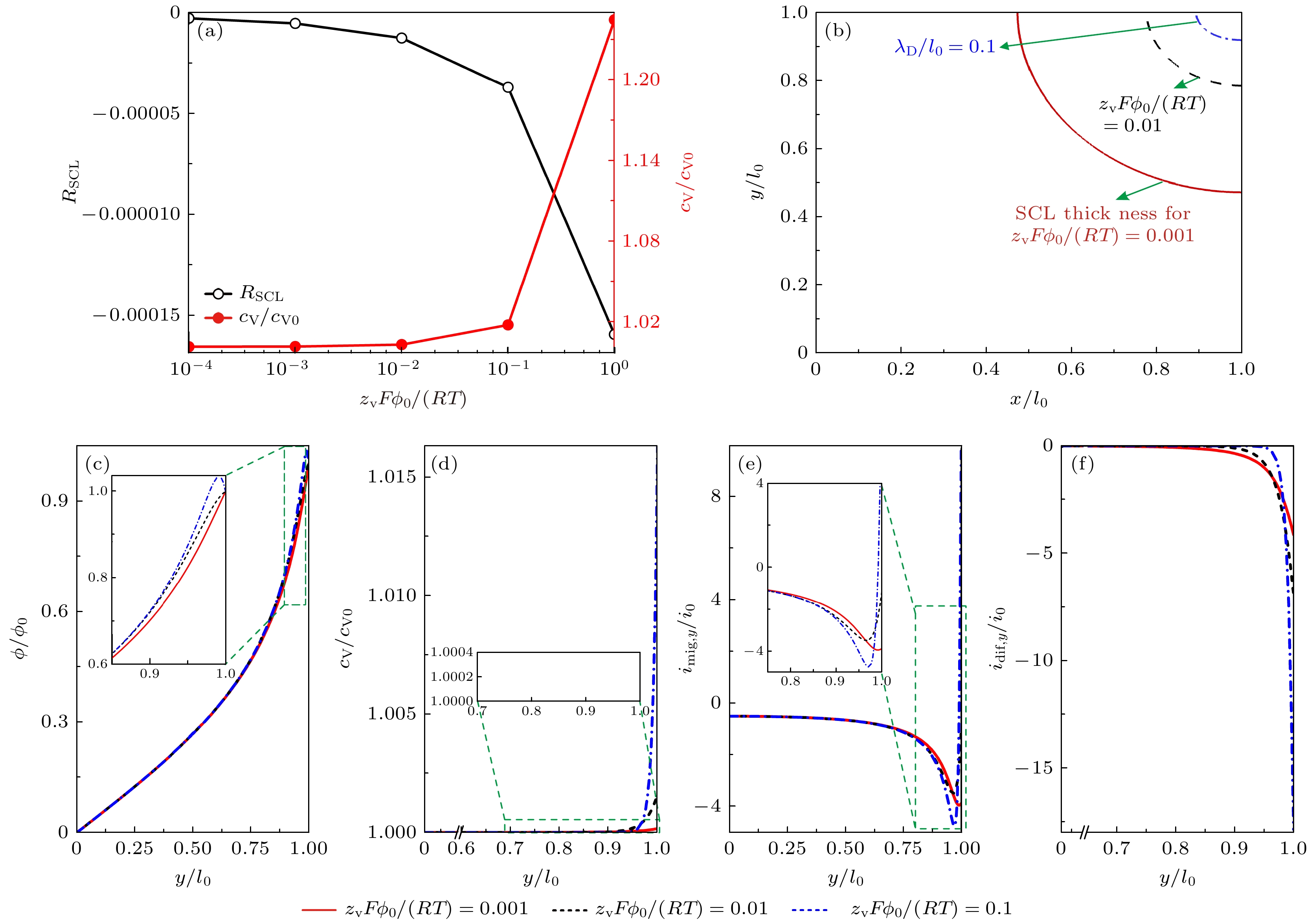
图 7 不同无量纲电势(zVFϕ0/(RT ))下SCL效应的影响, 其中, 不同zVFϕ0/(RT )下SCL电阻与TPB中心点氧空位浓度(a)、以及SCL厚度(b)分布; 当zVFϕ0/(RT )分别为0.001, 0.01, 0.1, 以及x/l0 = 1时的界面电势(c)、氧空穴浓度(d)、迁移(e)与扩散(f)电流密度分布
Fig. 7. Influences of SCL effect under different dimensionless potential (zVFϕ0/(RT )): The SCL resistance, oxygen vacancy concentration at central TPB (a), and SCL thickness (b) under different zVFϕ0/(RT ); distributions of potential (c), oxygen vacancy concentration (d), migration (e) and diffusion (f) current density when zVFϕ0/(RT ) = 0.001, 0.01 and 0.1 at x/l0 = 1.
表 1 本文的边界条件
Table 1. Boundary conditions of the present study.
坐标 边界条件 $ y^* = 0 $ $ \phi^* = 0, ~c_{\rm V}^* = 1 $ $ y^* = 1 $ (非TPBs) ${ {\partial \phi {^*} } / {\partial y^* } }= { {\partial c_{ {\rm V} }^*} / {\partial y^*} } = 0$ $ y^* = 1 $ (TPBs) ϕ* = 1, $ {i}_{\mathrm{a}\mathrm{V}}^{*} $ = –0.4 (基准工况) $ x^* = 0 $与$ x^* = 1 $ ${ {\partial \phi {^*} } / {\partial x^* } }= { {\partial {c_{\rm{V} } }{^*} } / {\partial x^*} } = 0$ 
下载: 导出CSV
-
[1] Wachsman E D, Lee K T 2011 Science 334 935
Google Scholar
[2] Gao Z, Mogni L V, Miller E C, Railsback J G, Barnett S A 2016 Energy Environ. Sci. 9 1602
Google Scholar
[3] Tong X, Mebane D S, De Souza R A 2020 J. Am. Ceram. Soc. 103 5
Google Scholar
[4] Zhao C, Li Y, Zhang W, Zheng Y, Lou X, Yu B, Chen J, Chen Y, Liu M, Wang J 2020 Energy Environ. Sci. 13 53
Google Scholar
[5] Lynch M E, Yang L, Qin W, Choi J, Liu M, Blinn K, Liu M 2011 Energy Environ. Sci. 4 2249
Google Scholar
[6] Zheng Y, Zhao C H, Li Y F, Zhang W Q, Wu T, Wang Z C, Li Z P, Chen J, Wang J C, Yu B, Zhang J J 2020 Nano Energy 78 105236
Google Scholar
[7] Uthayakumar A, Pandiyan A, Mathiyalagan S, Keshri A K, Moorthy S B K 2020 J. Phys. Chem. C 124 5591
Google Scholar
[8] Uthayakumar A, Pandiyan A, Krishna Moorthy S B 2018 Int. J. Hydrogen Energy 43 23488
Google Scholar
[9] Shirpour M, Merkle R, Lin C T, Maier J 2012 Phys. Chem. Chem. Phys. 14 730
Google Scholar
[10] Iguchi F, Chen C, Yugami H, Kim S 2011 J. Mater. Chem. 21 16517
Google Scholar
[11] Preethi S, Babu K S 2019 J. Alloys Compd. 792 1068
Google Scholar
[12] Kim S 2016 Phys. Chem. Chem. Phys. 18 19787
Google Scholar
[13] Kim S, Kim S K, Khodorov S, Maier J, Lubomirsky I 2016 Phys. Chem. Chem. Phys. 18 3023
Google Scholar
[14] Guan L L, Le S R, He S F, Zhu X D, Liu T, Sun K N 2015 Electrochim. Acta 161 129
Google Scholar
[15] Kim S K, Khodorov S, Chen C, Kim S, Lubomirsky I 2013 Phys. Chem. Chem. Phys. 15 8716
Google Scholar
[16] Kim S, Jain P, Avila-Paredes H J, Thron A, Benthem K V, SEN S 2010 J. Mater. Chem. 20 3855
Google Scholar
[17] Mebane D S, De Souza R A 2015 Energy Environ. Sci. 8 2935
Google Scholar
[18] Wang M, Kang Q 2010 J. Comput. Phys. 229 728
Google Scholar
[19] 徐晗, 张璐 2021 70 068801
Xu H, Zhang L 2021 Acta Phys. Sin. 70 068801
[20] Gregori G, Merkle R, Maier J 2017 Prog. Mater Sci. 89 252
Google Scholar
[21] Xu H, Chen Y, Kim J H, Dang Z, Liu M L 2019 Int. J. Hydrogen Energy 44 30293
Google Scholar
[22] 徐晗, 张璐, 党政 2020 69 098801
Google Scholar
Xu H, Zhang L, Dang Z 2020 Acta Phys. Sin. 69 098801
Google Scholar
[23] Xu H, Dang Z 2017 Int. J. Heat Mass Transfer 109 1252
Google Scholar
[24] Dang Z, Xu H 2016 Energy 107 295
Google Scholar
[25] Guo Z Z, Zheng C G, Shi B C 2002 Chin. Phys. 11 366
Google Scholar
[26] Connor P A, Yue X, Savaniu C D, Price R, Triantafyllou G, Cassidy M, Kerherve G, Payne D J, Maher R C, Cohen L F, Tomov R I, Glowacki B A, Kumar R V, Irvine J T S 2018 Adv. Energy Mater. 8 1800120
Google Scholar
[27] Chen Y, Chen Y, Ding D, Ding Y, Choi Y M, Zhang L, Yoo S, Chen D, deGlee B, Xu H, Lu Q, Zhao B, Vardar G, Wang J, Bluhme H, Crumline E J, Yang C, Liu J, Yildiz B, Liu M 2017 Energy Environ. Sci. 10 964
Google Scholar
[28] Zhang Y, Liu J, Singh M, Hu E, Jiang Z, Raza R, Wang F, Wang J, Yang F, Zhu B 2020 Nano-Micro Lett. 12 178
Google Scholar
[29] Zhu B 2009 Int. J. Energy Res. 33 1126
Google Scholar
[30] Zhu B, Li S, Mellander B E 2008 Electrochem. Commun. 10 302
Google Scholar
[31] 郭向欣, 李泓 2011 物理 40 648
Guo X, Li H 2011 Physics 40 648
[32] Crumlin E J, Mutoro E, Ahn S, La O G J, Leonard D N, Borisevich A, Biegalski M D, Christen H M, Shao-Horn Y 2010 J. Phys. Chem. Lett. 1 3149
Google Scholar
[33] 工藤徹一, 笛木和雄 (董治长 译) 1992 固态离子学 (北京: 北京工业大学出版社) 第35页
Kudo T, Fueki K (translated by Dong Z C) 1992 Solid Ionics (Beijing: Beijing University of Technology Press) p35 (in Chinese)
下载:
计量
- 文章访问数: 6447
- PDF下载量: 101
- 被引次数: 0
