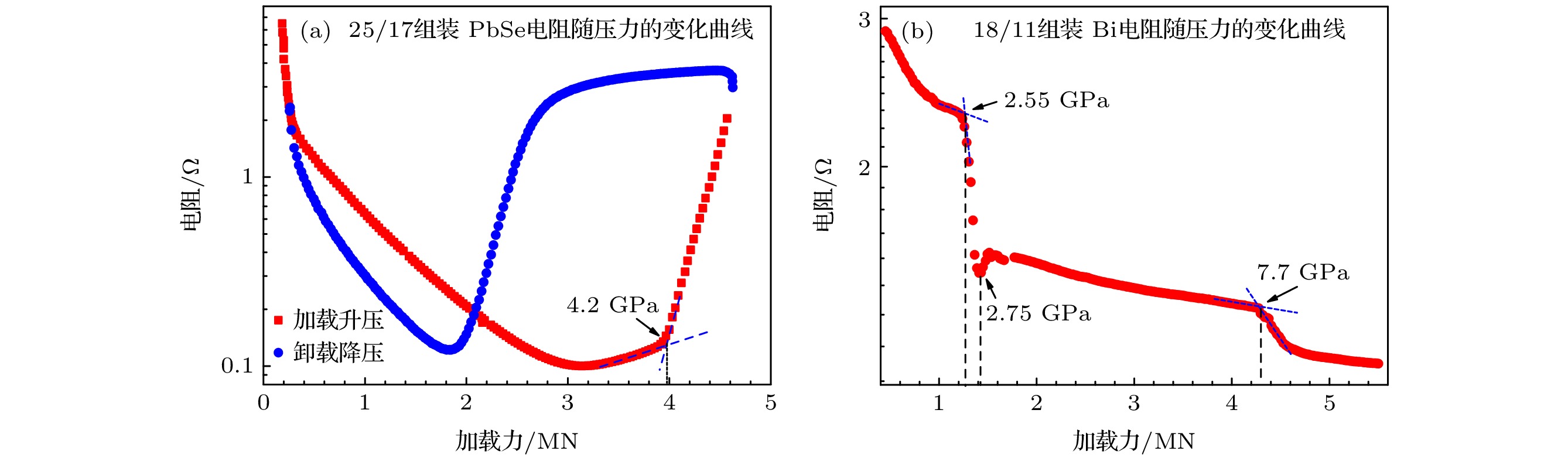
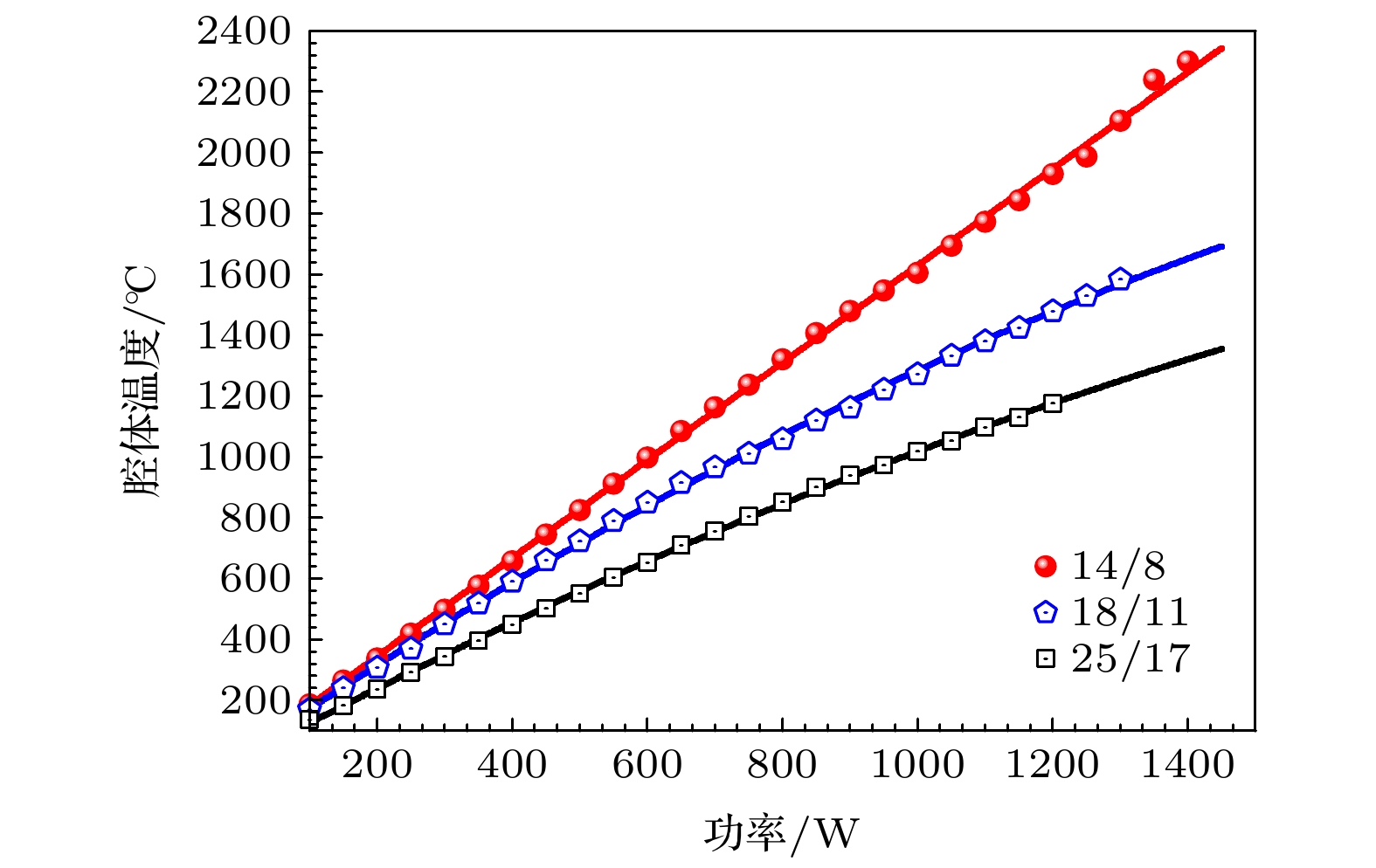
-
自八面腔静高压装置问世以来, 一定尺寸的二级压砧上可获得的最大腔体体积一直是一个被忽略的问题. 本工作通过八面体压腔的密封简化模型, 计算出加载后密封边可流动空间的最大体积, 进而确定出一定尺寸的二级压砧上可运行的最大腔体组装, 并以边长为25.4 mm的二级压砧为例, 计算了不同八面体边长与立方块截角边长的组合(八面体传压介质边长/二级压砧截角边长为18/11和25/17组装), 不同八面体初始形状(八面体倒棱与否)加载后的密封边可流动空间的最大体积, 并根据计算结果选定预密封条尺寸. 在边长为25.4 mm的碳化钨立方块上, 以叶腊石八面体为传压介质, 对18/11和25/17组装进行压力标定实验. 实验结果表明本工作中关于密封边体积的计算结果成立, 同时在25.4 mm的碳化钨二级压砧上实现了25/17组装的稳定运行, 获得接近厘米级的样品腔尺寸.Since the invention of split sphere multianvil apparatus, the maximum sample size that can be obtained on tungsten carbide (WC) anvils with a certain size has always been a neglected issue. The maximum volume of loaded gaskets and the maximum multianvil cell assembly operating on given size WC anvils are calculated by a simplified geometric model. As a concrete example, the maximum volume of loaded gaskets in different assemblies (18/11, 25/17 (octahedral edge-length/anvil truncation edge-length, in millimetre)) and different initial shapes of octahedrons (octahedron chamfered or not) running on WC anvils with 25.4 mm edge-length are calculated. The maximum initial sizes of gaskets in different assemblies are also calculated according to the maximum volume of loaded gaskets. Using the pyrophyllite octahedron as the pressure transmission medium, the pressure calibration of 14/8, 18/11, and 25/17 assembly are carried out on WC cubes, of which the edge-length is 25.4 mm, to verify the calculated results. The cell pressure is calibrated by in situ observing resistance change caused by phase transition of pressure calibration material at high pressure. All assemblies run stably and no blow-out phenomenon occurs. The experimental results show that the pressure transfer efficiency of 18/11 and 25/17 assembly with chamfered octahedron are better than previous reported results in the same pressure range. The experimental results also indicate that the calculations of the gasket in this work are valid. And the 25/17 assembly with chamfered octahedron can run stably on WC cube with 25.4 mm edge-length. In addition, using graphite tubes as heater, heating structure designs of different assemblies (14/8, 18/11, 25/17) are completed, in which the 14/8 assembly can achieve the highest temperature of 2300 ℃. The diameter of sample chamber is almost one centimeter in 25/17 assembly. This work contributes to the development of assembly techniques for secondary anvil made of polycrystalline diamond materials to obtain larger sample volumes under higher pressure conditions.
-
Keywords:
- multianvil apparatus /
- gasket /
- pressure calibration
[1] Kawai N, Endo S 1970 Rev. Sci. Instrum. 41 1178
Google Scholar
[2] Ohtani E, Irifune T, Hibberson W O, Ringwood A E 1987 High Temperature High Pressure 19 523
[3] Irifune T, Adachi Y, Fujino K, Ohtani E, Yoneda A, Sawamoto H 1992 High Pressure Res. 67 43
[4] Walker D, Carpenter M A, Hrrch C M 1990 Amer. Miner. 75 1020
[5] Shang Y S, Sheng F R, Hou X Y, Cheng L Y, Hu K 2020 Chin. Phys. Lett. 37 30
[6] 王福龙, 贺端威, 房雷鸣, 陈晓芳, 李拥军, 张伟, 张剑, 寇自力, 彭放 2008 57 5429
Google Scholar
Wang F L, He D W, Fang L M, Chen X F, Li Y J, Zhang W, Zhang J, Kou Z L, Peng F 2008 Acta Phys. Sin. 57 5429
Google Scholar
[7] 王文丹, 贺端威, 王海阔, 王福龙, 董海妮, 陈海花, 李子扬, 张剑, 王善民, 寇自力, 彭放 2010 59 3107
Google Scholar
Wang W D, He D W, Wang H K, Wang F L, Dong H N, Chen H H, Li Z Y, Zhang J, Wang S M, Kou Z L, Peng F 2010 Acta Phys. Sin. 59 3107
Google Scholar
[8] Ohtani E, Kagawa N, shimomura O, Togaya M, Suito K, Onodera A, Sawamoto H, Ito E, Kikegawa T 1989 Rev. Sci. Instrum. 60 922
Google Scholar
[9] Yamazaki D, Ito EYoshino T, Tsujino N, Yoneda A, Guo X, Xu F, Higo Y, Funakoshi K 2014 Phys. Earth Planet. Int. 228 262
Google Scholar
[10] Irifune T, Kunimoto T, Shinmei T 2019 C. R. Geosci. 351 260
Google Scholar
[11] Frost D J, Poe B T, Trnnes R G, Liebske C, Duba A, Rubie D C 2004 Phys. Earth Planet. Int. 143 507
[12] Shatskiy A, Katsura T, Litasov K D, Shcherbakova A V, Ito E 2011 Phys. Earth Planet. Int. 189 92
Google Scholar
[13] Shatskiy A, Borzdov Y M, Litasov K D, Ohtani E, Khokhryakov A F 2011 Am. Mineral. 96 541
Google Scholar
[14] 何飞, 贺端威, 马迎功, 晏小智, 刘方明, 彭放 2015 高压 3 161
Google Scholar
He F, He D W, Ma Y G, Yan X Z, Liu F M, Peng F 2015 Chin. J. High Pressure Phys. 3 161
Google Scholar
[15] 马迎功, 贺端威, 韩晶晶, 王强, 刘进, 王永华, 刘方明, 丁未, 寇自力 2017 高压 1 61
Google Scholar
Ma Y G, He D W, Han J J, Wang Q, Liu J, Wang Y H, Liu F M, Ding W, Kou Z L 2017 Chin J High Pressure Phys. 1 61
Google Scholar
[16] 王强, 贺端威, 刘进, 刘方明, 丁未, 马迎功, 刘腾, 李媛媛, 吴京军, 张佳威, 寇自力 2017 高压 5 511
Google Scholar
Wang Q, He D W, Liu J, Liu F M, Ding W, Ma Y G, Liu T, Li Y Y, Wu J J, Zhang J W, Kou Z L 2017 Chin. J. High Pressure Phys. 5 511
Google Scholar
[17] Pawley A R, Clark S M, Chinnery N J 2002 Amer. Miner. 87 1172
Google Scholar
[18] Fang L M, He D W, Chen C, Ding L Y, Luo X J 2007 High Pressure Res. 27 367
Google Scholar
[19] Stoyanov E, Ussermann U, Leinenweber K 2010 High Pressure Res. 30 175
Google Scholar
[20] 吕世杰, 罗建太, 苏磊, 胡云, 袁朝圣, 洪时明 2009 58 6852
Google Scholar
Lv S J, Luo J T, Su L, Hu Y, Yuan C S, Hong S M 2009 Acta Phys. Sin. 58 6852
Google Scholar
[21] 吕世杰 2007 博士学位论文 (成都: 西南交通大学)
Lü S J 2007 Ph. D. Dissertation (Chengdu: Southwest Jiaotong University) (in Chinese)
[22] Yoneda A, Endo S 1980 J. Appl. Phys. 51 3216
Google Scholar
[23] Getting I C 1998 Metrologia. 35 119
Google Scholar
[24] Chattopadhyay T, Schnering H G V, Grosshans W A 1986 Phys. B+C. 139 356
[25] Ovsyannikov S V, Shchennikov V V, Popova S V 2010 Phys. Status Solidi. 235 521
[26] Ovsyannikov S V, Shchennikov V V 2004 Solid State Commun. 132 333
Google Scholar
-
图 1 加载前后八面腔压机密封边的形态示意图 (a) 加载前的预密封条; (b)加载后预密封条受挤压流动形成的密封边区域
Fig. 1. Schematic diagram of the gaskets before and after loading: (a) The gaskets before loading; (b) the flowing area of gaskets after loading.
图 4 加热组装示意图 (a) 18/11组装; (b) 25/17组装
Fig. 4. Schematic diagram of heating assemblies: (a) 18/11 assembly; (b) 25/17 assembly.
图 5 实验使用的部分标压物质 (a) PbSe和(b) Bi的电阻随荷载变化的曲线
Fig. 5. Representative recorded resistances of (a) PbSe and (b) Bi respectively, as a function of press load.
图 6 不同组装腔体的压力标定结果, 插图为碳化钨二级压砧和叶腊石预密封条都相同的条件下, 14/8组装分别以叶腊石和氧化镁为八面体传压介质的压力标定结果
Fig. 6. Pressure calibration of different assemblies. Insert is the pressure calibration of 14/8 assembly with different octahedron of pyrophyllite and semi-sintered magnesia.
图 7 三种加热组装的腔体温度与功率的关系曲线. 14/8, 18/11, 25/17加热组装进行加温测试的腔体压力分别约为10, 7.7, 5.2 GPa.
Fig. 7. Temperature calibration of 14/8, 18/11 and 25/17 assemblies. The cell pressures for heating test were approximate 10, 7.7, and 5.2 GPa respectively.
图 8 加载后三种组装的密封边流动区域 (a) 18/11组装八面体磨倒棱; (b) 18/11组装八面体未磨倒棱; (c) 25/17组装八面体磨倒棱
Fig. 8. The areas of loaded gaskets in different assembly: (a) 18/11 assembly with chamfered octahedron; (b) 18/11 assembly with unchamfered octahedron; (c) 25/17 assembly with chamfered octahedron.
表 1 各符号及其含义
Table 1. Symbols and the meaning of the symbols.
符号 符号的含义 a 八面体初始边长 b 碳化钨立方块截角边长 l 立方块二级压砧的边长 Rmax 一个密封平面上密封边形成的圆形区域的最大半径, ${R_{\max }} = l + t/2$ S1 加载结束后八面腔内剩余的八面体传压介质在一个密封平面上的投影面积, ${S_1} = {b^2} + {t^2} + 2\sqrt 2 bt$ S2 部分八面体传压介质流入一个密封平面内形成的区域, $ {S}_{2}t=\Delta V/3=(0.9{V}_{0}-{V}_{\text{八面体}})/3$ S3 一个密封平面内预先放置的叶腊石预密封条受挤压形成的区域, ${S_3} = {\text{π}}{R^2} - {S_1} - {S_2}$ t0 叶腊石预密封条的初始厚度, ${t_0} = \sqrt 2 (a - b)/3$[12] t 加载结束后密封边的厚度 V0 八面体传压介质的初始体积, ${V_0} = \sqrt 2 {a^3}/3$ V八面体 加载结束后八面腔内剩余的八面体传压介质的体积, $ {V}_{\text{八面体}}=\sqrt{2}{b}^{3}/3+3{b}^{2}t+3\sqrt{2}b{t}^{2}+{t}^{3}$[12] ΔV 加载结束后流入相互垂直的3个密封平面内的部分八面体传压介质的总体积, $ \Delta V=0.9{V}_{0}-{V}_{\text{八面体}}$ V叶腊石密封边 一个密封平面上叶腊石预密封条形成的密封边的体积, $ {V}_{\text{叶腊石密封边}}={S}_{3}t=({\text{π}}{R}^{2}-{S}_{1}-{S}_{2})\times t$ Vmax叶腊石密封边 一个密封平面上叶腊石预密封条形成的密封边的最大体积, $ {V}_{\mathrm{max}}{}_{\text{叶腊石密封边}}=[{\text{π}}{(l+t/2)}^{2}-{S}_{1}-{S}_{2}]\times t$ V预密封条 一个预密封条的体积, $ {V}_{\text{预密封条}}={S}_{\text{梯形}}\times {t}_{0}=(a+w)w\times {t}_{0}$ Vmax预密封条 一个密封平面上叶腊石预密封条的最大体积, $ {V}_{\mathrm{max}{\text{预密封条}}}=4{V}_{\text{预密封条}}=4(a+w)w\times {t}_{0}={V}_{{\max}{\text{叶腊石密封边}}}/0.9$ w 预密封条宽度 wmax 预密封条的最大宽度 
下载: 导出CSV
表 3 各种组装加载后的密封边厚度t与预密封条最大宽度wmax的对应关系
Table 3. The calculated maximum width wmax of the gaskets before loading, corresponding to the thickness t of loaded gaskets in different assemblies.
组装类型 加载后密封边
的厚度t/mm对应的预密封条
最大宽度wmax/mm18/11磨倒棱 1.4 8.03 1.6 9.05 1.8 10.03 18/11未磨倒棱 1.4 6.86 1.6 7.89 1.8 8.87 25/17磨倒棱 1.8 6.37 2.0 7.19 2.2 7.98 25/17未磨倒棱 1.8 4.74 2.0 5.57 2.2 6.38
下载: 导出CSV
-
[1] Kawai N, Endo S 1970 Rev. Sci. Instrum. 41 1178
Google Scholar
[2] Ohtani E, Irifune T, Hibberson W O, Ringwood A E 1987 High Temperature High Pressure 19 523
[3] Irifune T, Adachi Y, Fujino K, Ohtani E, Yoneda A, Sawamoto H 1992 High Pressure Res. 67 43
[4] Walker D, Carpenter M A, Hrrch C M 1990 Amer. Miner. 75 1020
[5] Shang Y S, Sheng F R, Hou X Y, Cheng L Y, Hu K 2020 Chin. Phys. Lett. 37 30
[6] 王福龙, 贺端威, 房雷鸣, 陈晓芳, 李拥军, 张伟, 张剑, 寇自力, 彭放 2008 57 5429
Google Scholar
Wang F L, He D W, Fang L M, Chen X F, Li Y J, Zhang W, Zhang J, Kou Z L, Peng F 2008 Acta Phys. Sin. 57 5429
Google Scholar
[7] 王文丹, 贺端威, 王海阔, 王福龙, 董海妮, 陈海花, 李子扬, 张剑, 王善民, 寇自力, 彭放 2010 59 3107
Google Scholar
Wang W D, He D W, Wang H K, Wang F L, Dong H N, Chen H H, Li Z Y, Zhang J, Wang S M, Kou Z L, Peng F 2010 Acta Phys. Sin. 59 3107
Google Scholar
[8] Ohtani E, Kagawa N, shimomura O, Togaya M, Suito K, Onodera A, Sawamoto H, Ito E, Kikegawa T 1989 Rev. Sci. Instrum. 60 922
Google Scholar
[9] Yamazaki D, Ito EYoshino T, Tsujino N, Yoneda A, Guo X, Xu F, Higo Y, Funakoshi K 2014 Phys. Earth Planet. Int. 228 262
Google Scholar
[10] Irifune T, Kunimoto T, Shinmei T 2019 C. R. Geosci. 351 260
Google Scholar
[11] Frost D J, Poe B T, Trnnes R G, Liebske C, Duba A, Rubie D C 2004 Phys. Earth Planet. Int. 143 507
[12] Shatskiy A, Katsura T, Litasov K D, Shcherbakova A V, Ito E 2011 Phys. Earth Planet. Int. 189 92
Google Scholar
[13] Shatskiy A, Borzdov Y M, Litasov K D, Ohtani E, Khokhryakov A F 2011 Am. Mineral. 96 541
Google Scholar
[14] 何飞, 贺端威, 马迎功, 晏小智, 刘方明, 彭放 2015 高压 3 161
Google Scholar
He F, He D W, Ma Y G, Yan X Z, Liu F M, Peng F 2015 Chin. J. High Pressure Phys. 3 161
Google Scholar
[15] 马迎功, 贺端威, 韩晶晶, 王强, 刘进, 王永华, 刘方明, 丁未, 寇自力 2017 高压 1 61
Google Scholar
Ma Y G, He D W, Han J J, Wang Q, Liu J, Wang Y H, Liu F M, Ding W, Kou Z L 2017 Chin J High Pressure Phys. 1 61
Google Scholar
[16] 王强, 贺端威, 刘进, 刘方明, 丁未, 马迎功, 刘腾, 李媛媛, 吴京军, 张佳威, 寇自力 2017 高压 5 511
Google Scholar
Wang Q, He D W, Liu J, Liu F M, Ding W, Ma Y G, Liu T, Li Y Y, Wu J J, Zhang J W, Kou Z L 2017 Chin. J. High Pressure Phys. 5 511
Google Scholar
[17] Pawley A R, Clark S M, Chinnery N J 2002 Amer. Miner. 87 1172
Google Scholar
[18] Fang L M, He D W, Chen C, Ding L Y, Luo X J 2007 High Pressure Res. 27 367
Google Scholar
[19] Stoyanov E, Ussermann U, Leinenweber K 2010 High Pressure Res. 30 175
Google Scholar
[20] 吕世杰, 罗建太, 苏磊, 胡云, 袁朝圣, 洪时明 2009 58 6852
Google Scholar
Lv S J, Luo J T, Su L, Hu Y, Yuan C S, Hong S M 2009 Acta Phys. Sin. 58 6852
Google Scholar
[21] 吕世杰 2007 博士学位论文 (成都: 西南交通大学)
Lü S J 2007 Ph. D. Dissertation (Chengdu: Southwest Jiaotong University) (in Chinese)
[22] Yoneda A, Endo S 1980 J. Appl. Phys. 51 3216
Google Scholar
[23] Getting I C 1998 Metrologia. 35 119
Google Scholar
[24] Chattopadhyay T, Schnering H G V, Grosshans W A 1986 Phys. B+C. 139 356
[25] Ovsyannikov S V, Shchennikov V V, Popova S V 2010 Phys. Status Solidi. 235 521
[26] Ovsyannikov S V, Shchennikov V V 2004 Solid State Commun. 132 333
Google Scholar
下载:
计量
- 文章访问数: 4915
- PDF下载量: 69
- 被引次数: 0
