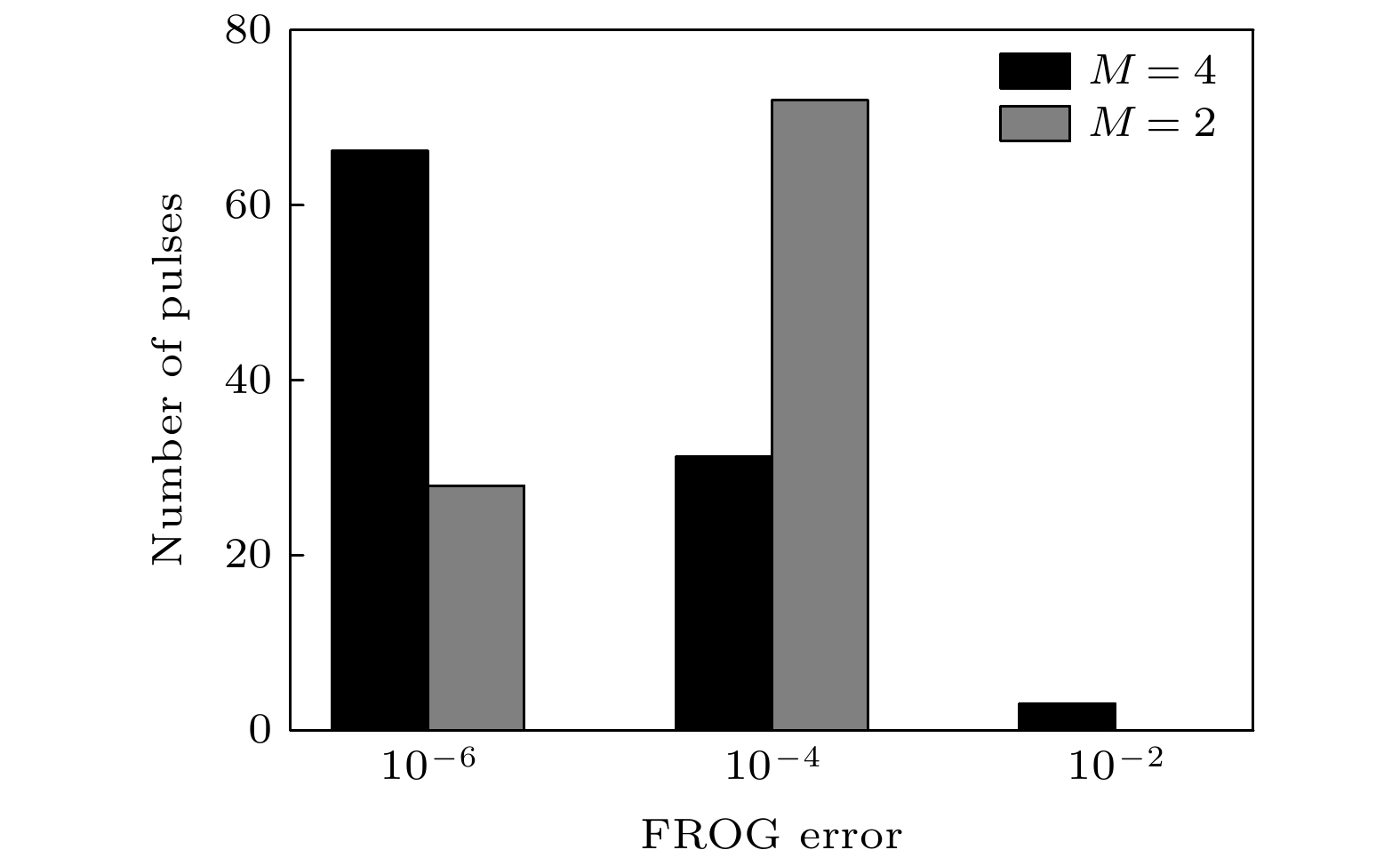
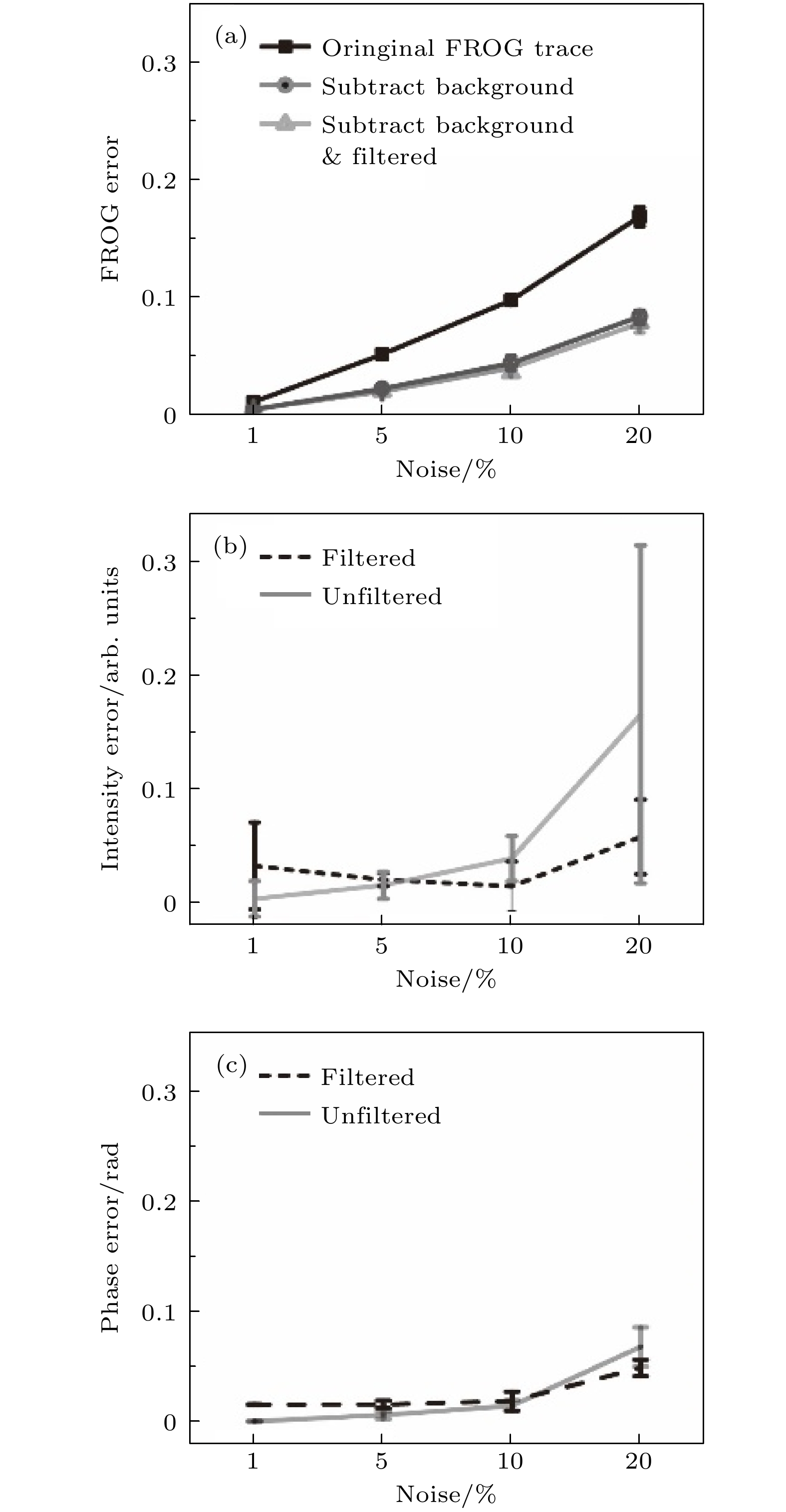
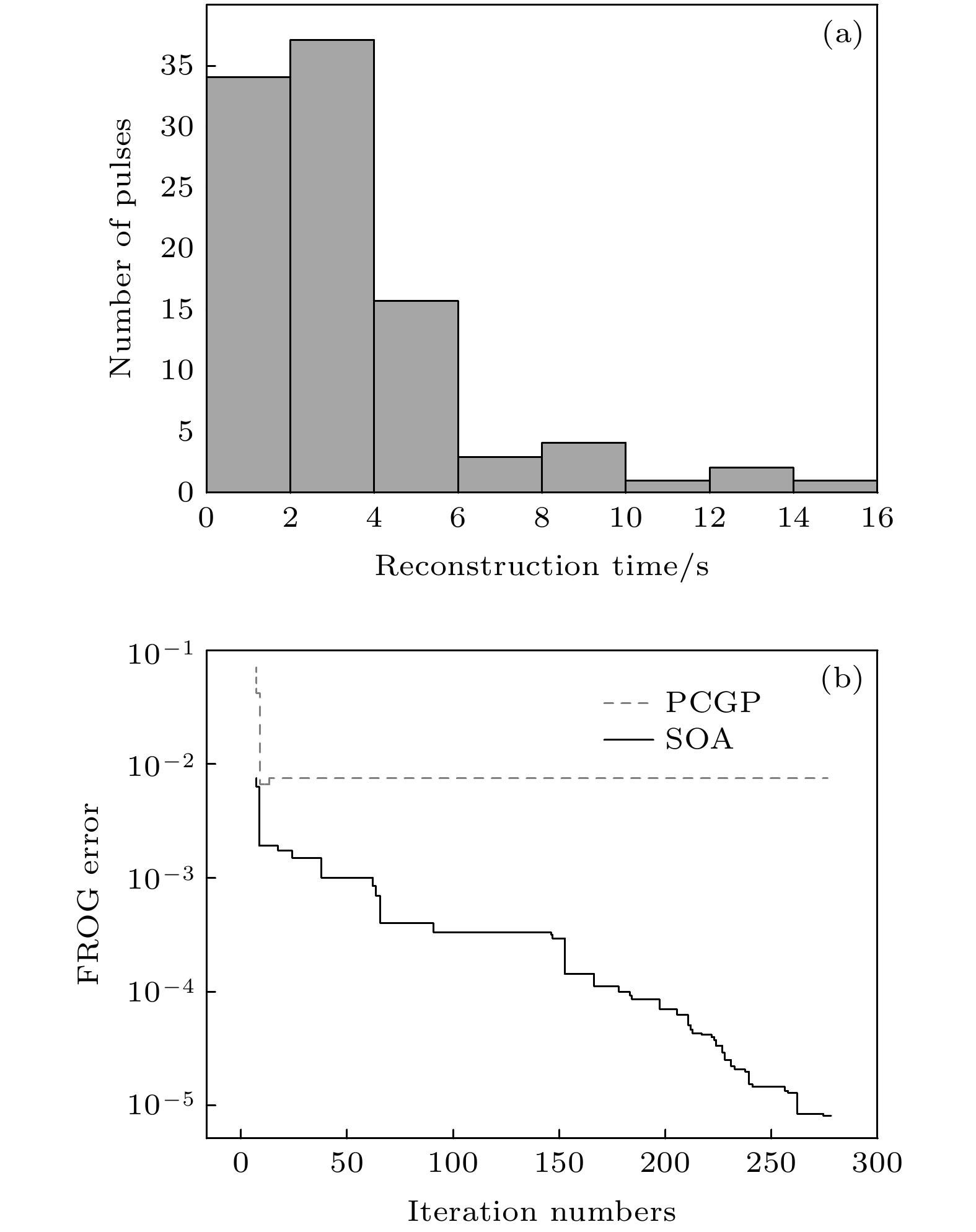
-
频率分辨光学开关(frequency-resolved optical gating, FROG)法是目前测量超短激光脉冲的主要方法之一. 针对其常用的主成分广义投影重构(principal component generalized projections, PCGP)算法在处理大矩阵FROG谱图时速度会减慢及存在噪音时准确度下降的缺点, 本文提出一种基于搜寻者优化算法的FROG算法. 该算法在直接测量脉冲光谱分布的基础上, 通过搜索脉冲频域相位的几个色散系数, 从而恢复脉冲的结构. 由于新算法主要在频域上进行运算, 流程比PCGP算法简便很多, 收敛速度和准确性都有明显改善. 通过数值模拟方法重构了多个不同结构的超短脉冲, 分析讨论了无噪音和在不同噪音水平下该算法的准确度. 计算结果充分展示了该算法重构脉冲的速度快、准确度高的特点, 在无噪音条件下其准确度比PCGP提升了3个数量级以上.Frequency-resolved optical gating (FROG) is a common technique of ultrashort pulse measurement. It reconstructs the test pulse by an iterative two-dimensional phase retrieval algorithm from a FROG trace. Now the most widely used FROG algorithm is principal component generalized projection (PCGP), yet its accuracy of pulse retrieval drops obviously under noise condition, and its iterative speed slows down significantly as the size of FROG trace increases. Actually, most of ultrashort pulses delivered from ultrafast oscillators and amplifiers as well as created in most scientific experiments are of smooth spectral phases, so that they can be determined by a few of dispersion coefficients. In this paper, we propose a FROG algorithm based on seeker optimization algorithm (SOA). After recording the spectrum of the test pulse, several main dispersion coefficients of the spectral phase of the pulse are searched directly by the SOA algorithm to fit the corresponding FROG trace. Then the shape of the test pulse can be uniquely reconstructed. Since this algorithm mainly operates in a spectral domain and its routine of iteration is much simpler than PCGP’s, faster speed and higher accuracy of pulse retrieval can be expected. In order to prove the advantages of SOA-FROG algorithm, numeral simulations are performed for test pulses with varying dispersion, in the cases without noise and with 1%, 5%, 10%, 20% noise levels, respectively. The simulation results show that the new algorithm performs much better than PCGP in accuracy and iteration speed. In the case without noise, 97% test pulses reach the condition of rigid convergence (FROG error G ≤ 10–4) after 1500 iteration circles by using the SOA, with an average FROG error G < 10–5. So the accuracy of pulse reconstruction by SOA is at least three orders of magnitude higher than by PCGP. In cases with different noise levels, the accuracy of pulse reconstruction by SOA is also much higher than by PCGP. By means of background-subtraction and filtering on the FROG traces, the retrieved pulse profiles almost accord with reality. Typically for a 256 × 256 FROG trace, SOA-FROG iterates 100.8 circles per second, about 5 times faster than PCGP. After 300 iteration circles by SOA in about 3 s, most of test pulses can finish their routines of reconstruction and reach high accuracy. Besides SHG-FROG, the SOA-FROG algorithm can also be utilized in other FROG techniques based on the 3rd order nonlinear optical effects. In summary, the SOA-FROG is expected to be suitable to the real-time pulse measurement with high accuracy in most of application cases. Yet some measures of improvement should be taken to reconstruct complex pulses with rough spectral phases or/and broken spectra.
-
Keywords:
- frequency-resolved optical gating /
- ultrashort pulse /
- real time measurement /
- optimization algorithm
[1] Kane D J, Trebino R 1993 Opt. Lett. 18 823
Google Scholar
[2] 黄沛, 方少波, 黄杭东, 赵昆, 滕浩, 侯洵, 魏志义 2018 67 214202
Google Scholar
Huang P, Fang S B, Huang H D, Zhao K, Teng H, Hou X, Wei Z Y 2018 Acta Phys. Sin. 67 214202
Google Scholar
[3] Stibenz G, Steinmeyer G 2005 Opt. Express 13 2617
Google Scholar
[4] 王兆华, 魏志义, 滕浩, 王鹏, 张杰 2003 52 362
Google Scholar
Wang Z H, Wei Z Y, Teng H, Wang P, Zhang J 2003 Acta Phys. Sin. 52 362
Google Scholar
[5] 马晓璐, 李培丽, 郭海莉, 张一, 朱天阳, 曹凤娇 2014 63 240601
Google Scholar
Ma X L, Li P L, Guo H L, Zhang Y, Zhu T Y, Cao F J 2014 Acta Phys. Sin. 63 240601
Google Scholar
[6] 文锦辉, 胡婷, 吴琴菲 2019 68 110601
Google Scholar
Wen J H, Hu T, Wu Q F 2019 Acta Phys. Sin. 68 110601
Google Scholar
[7] DeLong K W, Fittinghoff D N, Trebino R, Kohler B, Wilson K 1994 Opt. Lett. 19 2152
Google Scholar
[8] Kane D J 1998 IEEE J. Quantum Electron. 3 4
Google Scholar
[9] Honzatko P, Kanka J, Vrany B 2004 Opt. Expess 12 6046
Google Scholar
[10] Nicholson J W, Omenetto F G, Funk D J, Taylor A J 1999 Opt. Lett. 24 490
Google Scholar
[11] DeLong K W, Ladera C L, Trebino R, Kohler B, Wilson K 1995 Opt. Lett. 20 486
Google Scholar
[12] Kane D J, Rodriguez G, Taylor A J 1997 J. Opt. Soc. Am. B 14 935
Google Scholar
[13] Kane D J 1999 IEEE J. Quantum Electron. 35 421
Google Scholar
[14] Kane D J 2008 J. Opt. Soc. Am. B 25 A120
Google Scholar
[15] Xu L N, Zeek E, Trebino R 2008 J. Opt. Soc. Am. B 25 A70
Google Scholar
[16] Wong T C, Ratner J, Vikrant C H, Trebino R 2012 J. Opt. Soc. Am. B 29 1237
Google Scholar
[17] Kane D J 2013 Lasers & Electro-Optics San Jose, CA, USA, June 9-14, 2013 paper JTh2A.16
[18] Kane D J, Omenetto F G, Taylor A J 2000 Opt. Lett. 25 1216
Google Scholar
[19] Hause A, Kraft S, Rohrmann P, Mitschke F 2015 J. Opt. Soc. Am. B 32 868
Google Scholar
[20] Kane D J 2017 Conference on Lasers and Electro-Optics San Jose, CA, USA, May 14-19, 2017 Paper STu3I.4
[21] 戴朝华 2009 博士学位论文(成都: 西南交通大学)
Dai C H 2009 Ph. D. Dissertation (Chengdu: Southwest Jiaotong University) (in Chinese)
[22] Dai C H, Chen W R, Song Y H, Zhu Y F 2010 J. Systems Eng. Electro. 21 300
Google Scholar
[23] Tuba M, Bacanin N 2014 Neurocomputing 143 197
Google Scholar
[24] Dai C H, Chen W R, Li L X, Zhu Y F, Yang Y X 2011 Phys. Rev. E 83 036203
Google Scholar
[25] Yang W L, Springer M, J Strohaber 2010 Opt. Expess 18 15028
Google Scholar
[26] Hong K H, Lee Y S, Nam C H 2007 Opt. Commun. 271 169
Google Scholar
[27] Fittinghoff D N, DeLong K W, Trebino R, Ladera C L 1995 J. Opt. Soc. Am. B 12 1955
Google Scholar
-
图 2 两类色散结构的随机脉冲经过SOA迭代运算1500次后的误差分布
Fig. 2. Distributions of FROG error at three levels for random ultrashort pulses of two chirped features after 1500 circles of iteration with SOA.
图 3 (a)脉冲3的原始SHG-FROG谱图; (b) SOA和PCGP两种算法重构出的脉冲3的时域强度和相位
Fig. 3. (a) Original SHG-FROG trace of pulse 3#; (b) reconstructed intensities and phases in time domain of the pulse by SOA and PCGP algorithm, respectively.
图 4 不同噪音水平下用SOA对脉冲1进行重构所对应的 (a) FROG误差、(b)强度误差和(c)相位误差
Fig. 4. (a) FROG error, (b) intensity error, and (c) phase error of test pulse 1# reconstructed by SOA with different noise levels.
图 5 不同噪音水平下重构脉冲1得到的FROG谱图和时域曲线
Fig. 5. Reconstructed FROG traces, intensities and phases in time domain of test pulse 1# by SOA algorithm with different noise levels.
图 6 (a)无噪音条件下用SOA重构随机色散脉冲的收敛时间范围; (b)两种算法对脉冲1重构迭代300次情形下其误差的演化过程
Fig. 6. (a) Distributions of pulse numbers via reconstruction time for SOA in cases without noise; (b) evolutions of FROG error for pulse 1# in 300 circles of iteration with SOA and PCGP algorithm, respectively.
表 1 无噪音情形下几个脉冲的重构结果
Table 1. Reconstructed results of three test pulses in cases without noise.
脉冲编号 原始脉冲色散系数 SOA-FROG计算结果 PCGP结果 GDD/fs2 TOD/fs3 FOD/fs4 FVOD/fs5 GDD/fs2 TOD/fs3 FOD/fs4 FVOD/fs5 $ \bar{G} $ $ \bar{G} $ 1 (M = 2) 150 –2000 5 80 150 –2000 0 0 4.0 × 10–6 1.1 × 10–2 2 (M = 4) 50 30 520 600 50 30 520 600 6.4 × 10–9 7.2 × 10–3 3 (M = 4) 100 –500 –3652 8000 100 –500 –3652 7999 1.2 × 10–5 9.8 × 10–3 
下载: 导出CSV
表 2 不同噪音水平下用SOA和PCGP算法重构脉冲1的结果比较
Table 2. Comparison of reconstructed results of pulse 1# by SOA and PCGP algorithms with different noise levels.
噪音水平/% SOA-FROG的重构结果 PCGP的重构结果 GDD/fs2 TOD/fs3 GI/% GP/% G/% GI /% GP/% G/% 1 –150 2002 0.01 0.08 0.33 4.44 16.3 0.87 5 154 –2105 1.95 0.78 1.31 14.0 20.1 1.88 10 153 –1940 0.02 2.61 2.01 13.2 13.6 3.46 20 193 –2651 1.52 5.77 3.77 20.0 22.3 4.62
下载: 导出CSV
-
[1] Kane D J, Trebino R 1993 Opt. Lett. 18 823
Google Scholar
[2] 黄沛, 方少波, 黄杭东, 赵昆, 滕浩, 侯洵, 魏志义 2018 67 214202
Google Scholar
Huang P, Fang S B, Huang H D, Zhao K, Teng H, Hou X, Wei Z Y 2018 Acta Phys. Sin. 67 214202
Google Scholar
[3] Stibenz G, Steinmeyer G 2005 Opt. Express 13 2617
Google Scholar
[4] 王兆华, 魏志义, 滕浩, 王鹏, 张杰 2003 52 362
Google Scholar
Wang Z H, Wei Z Y, Teng H, Wang P, Zhang J 2003 Acta Phys. Sin. 52 362
Google Scholar
[5] 马晓璐, 李培丽, 郭海莉, 张一, 朱天阳, 曹凤娇 2014 63 240601
Google Scholar
Ma X L, Li P L, Guo H L, Zhang Y, Zhu T Y, Cao F J 2014 Acta Phys. Sin. 63 240601
Google Scholar
[6] 文锦辉, 胡婷, 吴琴菲 2019 68 110601
Google Scholar
Wen J H, Hu T, Wu Q F 2019 Acta Phys. Sin. 68 110601
Google Scholar
[7] DeLong K W, Fittinghoff D N, Trebino R, Kohler B, Wilson K 1994 Opt. Lett. 19 2152
Google Scholar
[8] Kane D J 1998 IEEE J. Quantum Electron. 3 4
Google Scholar
[9] Honzatko P, Kanka J, Vrany B 2004 Opt. Expess 12 6046
Google Scholar
[10] Nicholson J W, Omenetto F G, Funk D J, Taylor A J 1999 Opt. Lett. 24 490
Google Scholar
[11] DeLong K W, Ladera C L, Trebino R, Kohler B, Wilson K 1995 Opt. Lett. 20 486
Google Scholar
[12] Kane D J, Rodriguez G, Taylor A J 1997 J. Opt. Soc. Am. B 14 935
Google Scholar
[13] Kane D J 1999 IEEE J. Quantum Electron. 35 421
Google Scholar
[14] Kane D J 2008 J. Opt. Soc. Am. B 25 A120
Google Scholar
[15] Xu L N, Zeek E, Trebino R 2008 J. Opt. Soc. Am. B 25 A70
Google Scholar
[16] Wong T C, Ratner J, Vikrant C H, Trebino R 2012 J. Opt. Soc. Am. B 29 1237
Google Scholar
[17] Kane D J 2013 Lasers & Electro-Optics San Jose, CA, USA, June 9-14, 2013 paper JTh2A.16
[18] Kane D J, Omenetto F G, Taylor A J 2000 Opt. Lett. 25 1216
Google Scholar
[19] Hause A, Kraft S, Rohrmann P, Mitschke F 2015 J. Opt. Soc. Am. B 32 868
Google Scholar
[20] Kane D J 2017 Conference on Lasers and Electro-Optics San Jose, CA, USA, May 14-19, 2017 Paper STu3I.4
[21] 戴朝华 2009 博士学位论文(成都: 西南交通大学)
Dai C H 2009 Ph. D. Dissertation (Chengdu: Southwest Jiaotong University) (in Chinese)
[22] Dai C H, Chen W R, Song Y H, Zhu Y F 2010 J. Systems Eng. Electro. 21 300
Google Scholar
[23] Tuba M, Bacanin N 2014 Neurocomputing 143 197
Google Scholar
[24] Dai C H, Chen W R, Li L X, Zhu Y F, Yang Y X 2011 Phys. Rev. E 83 036203
Google Scholar
[25] Yang W L, Springer M, J Strohaber 2010 Opt. Expess 18 15028
Google Scholar
[26] Hong K H, Lee Y S, Nam C H 2007 Opt. Commun. 271 169
Google Scholar
[27] Fittinghoff D N, DeLong K W, Trebino R, Ladera C L 1995 J. Opt. Soc. Am. B 12 1955
Google Scholar
下载:
计量
- 文章访问数: 5397
- PDF下载量: 78
- 被引次数: 0
