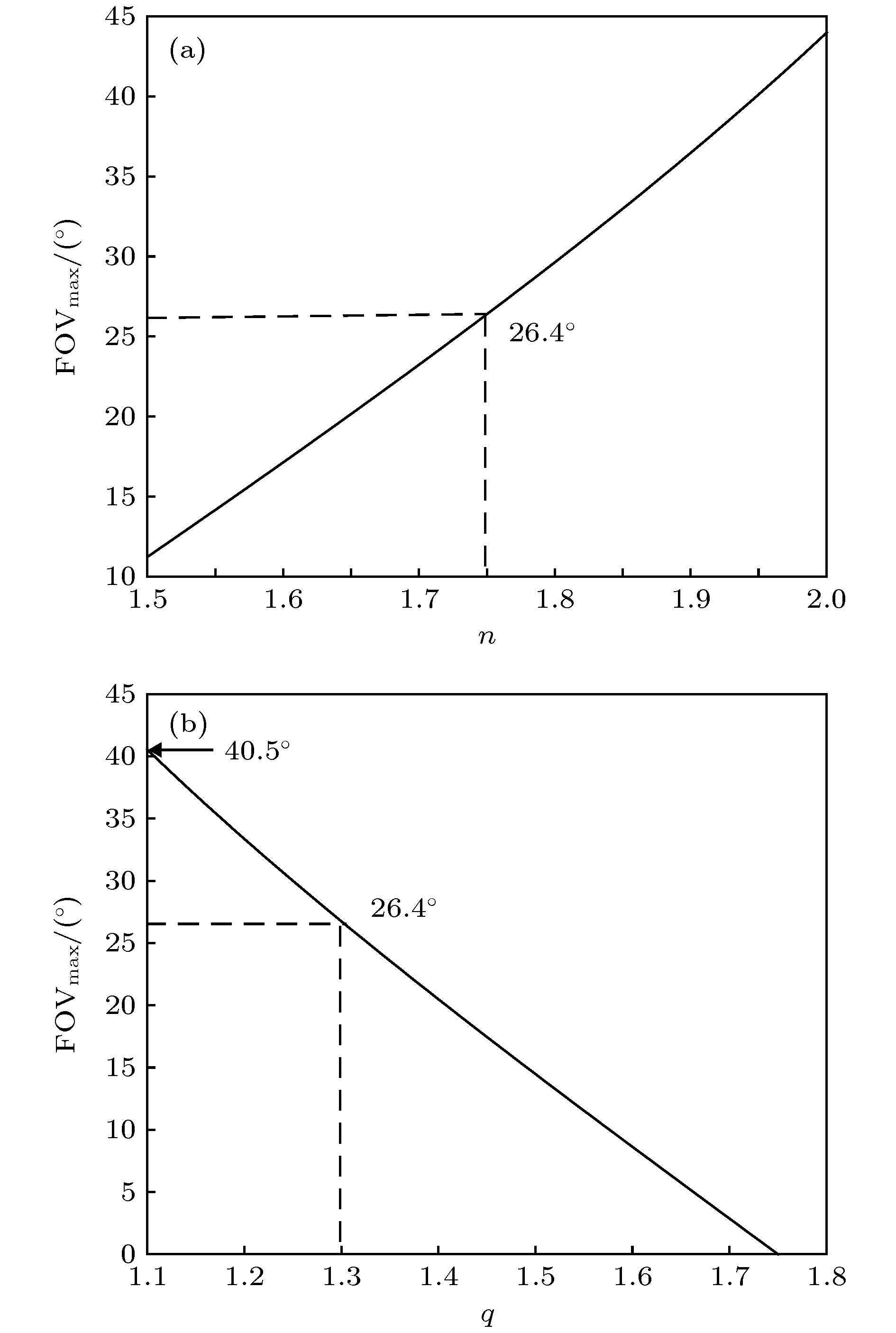
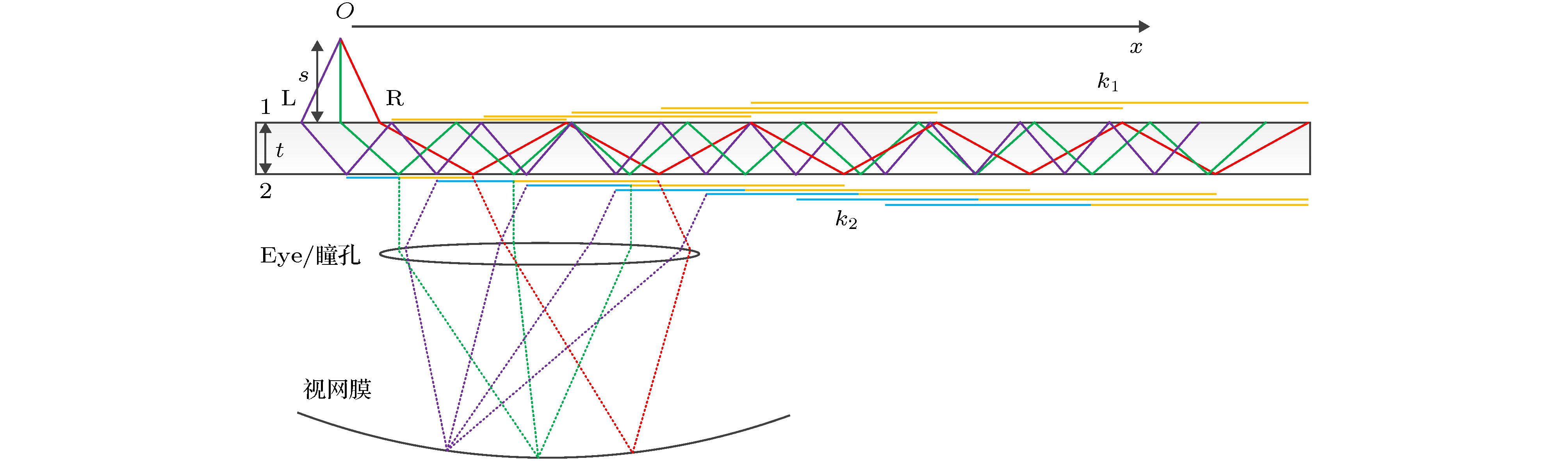
-
衍射光栅已在波导中得到广泛应用, 能将光束或图像从耦入端传输并在预定位置耦合输出, 不过在应用于诸如增强现实/虚拟现实等大视场角(field of view, FOV)、彩色光源时会存在FOV不匹配、视场缺失、出射不均匀等问题. 故从这些物理问题出发, 推导出衍射波导的FOV上限、视场完整的理论边界公式, 在此基础上再分别针对单色波和复色波进行深入研究. 得出单层衍射波导在常规高折射率n = 1.75条件下, 支持单色波FOV理论上限约48°, 支持复色波颜色系数q = 1.3的FOV理论上限26.4°, 更大FOV就需要配置更高折射率和更小q值. 视场完整性的边界条件表明, 减小长波的最大衍射角和减薄波导厚度就能解决视场缺失的问题, 实用最大衍射角一般不超过75°, 波导层厚度根据FOV大小一般在0.5—1.0 mm之间. 最后提出将各全内反射视场展开为光线追迹图的方法和瞳孔均摊接收各角度光能的分布函数, 就此可求解光栅耦出区的最佳位置, 并利用分布函数的倒数来约束投射光的角分布或者光栅效率的角分布, 以在任意位置都能接收均匀出射视场: 单色波导的均匀性从0.27提高到0.15, 单光栅复色波导中长波均匀性从0.40提高到0.28. 这些研究结果有助于解决衍射波导用于大FOV和复色光的难题.Diffraction gratings have been widely used in waveguides. They can transmit light beams or images from the in-coupling end to the out-coupling end at predetermined positions. However, when they are applied to augmented reality and virtual reality with large field of view and color light sources, there will arise some problems such as mismatch and missing field of view, non-uniform emission, and others. Therefore, starting from these physical problems, the upper limit of the field of view for diffractive waveguide and the complete theoretical boundary formula of the field of view are derived, and on this basis, in-depth research is conducted on monochromatic waves and multicolor waves, respectively. It is concluded that the single-layer diffractive waveguide supports the theoretical upper limit of the monochromatic wave field angle of about 48° under normal high refractive index of n = 1.75, and supports the theoretical upper limit of the multicolor wave field angle of 26.4° for coefficient q = 1.3. Clearly, a larger field of view requires a higher refractive index n and a smaller q value. The boundary conditions of field integrity indicate that reducing the maximum diffraction angle of the long wave and thinning the thickness of the waveguide layer can solve the problem of missing field of view. The practical maximum diffraction angle generally does not exceed 75°, and the thickness of the waveguide layer is about 0.5 to 1.0 mm generally based on the incident field of view. Finally, a method of expanding each total internal reflection field of view into a ray tracing diagram and a distribution function of pupils to receive light energy at various angles are obtained. In this way, the optimal position of the out-coupling grating region can be achieved, and the inverse of the distribution function is used to constrain the angular distribution of the projected light or the grating efficiency, and then receiving uniform exit image at any position becomes possible. The uniformity of the monochromatic waveguide increases from 0.27 to 0.15, and the uniformity of the long wave in the single grating multicolor waveguide rises from 0.4 to 0.28. The results of these studies will undoubtedly help to solve the problem in the diffractive waveguides used in large field of view and multicolor light.
-
Keywords:
- diffraction grating /
- planar waveguide /
- field of view /
- total internal reflection
[1] Miller J M, Beaucoudrey N, Chavel P, Turunen J, Cambril E 1997 Appl. Opt. 36 5717
Google Scholar
[2] Kimmel J, Levola T, Saarikko P, et al. 2008 JSID 16 351
Google Scholar
[3] Jagt H J B, Cornelissen H J, Bastiaansen C W M, Broer D J 2004 Adv. Mater. 16 2108
Google Scholar
[4] 周忠, 周颐, 肖江剑 2015 中国科学: 信息科学 45 157
Google Scholar
Zhou Z, Zhou Y, Xiao J J 2015 Sci.Sin. Info. 45 157
Google Scholar
[5] Chen H W, Weng Y S, Xu D M, Tabiryan N V, Wu S T 2016 Opt. Express 24 7287
Google Scholar
[6] 高源, 刘越, 程德文, 王涌天 2016 计算机辅助设计与图形学学报 28 896
Google Scholar
Gao Y, Liu Y, Cheng D W, Wang Y T 2016 J. of Computer-Aided Design & Computer Graphics 28 896
Google Scholar
[7] Lalanne P 1999 J. Opt. Soc. Am. A 16 2517
Google Scholar
[8] Saarikko P 2008 Proc. SPIE 7001 700105
Google Scholar
[9] 梁华伟, 石顺祥, 李家立 2007 56 2293
Google Scholar
Liang H W, Shi S X, Li J L 2007 Acta Phys. Sin. 56 2293
Google Scholar
[10] Liu Z Y, Pang Y J, Pan C, Huang Z H 2017 Opt. Express 25 30720
Google Scholar
[11] Levola T, Laakkonen P 2007 Opt. Express 15 2067
Google Scholar
[12] Amitai Y, Reinhom S, Friesem A A 1995 Appl. Opt. 34 1352
Google Scholar
[13] Levola T 2006 JSID 14 467
Google Scholar
[14] Kress B C 2019 Proc. SPIE 11062 110620J-1
[15] Zhang N N, Liu J, Han J, LI X, Yang F, Wang X, Hu B, Wang Y T 2015 Appl. Opt. 54 3645
Google Scholar
[16] 刘辉 2012 硕士学位论文 (杭州: 浙江大学)
Liu H 2012 M. S. Dissertation (Hangzhou: Zhejiang University) (in Chinese)
[17] Guo J J, Tu Y, Yang L L, Wang L L 2015 Opt. Engineering 54 232
[18] 曾飞, 张新 2014 中国光学 7 731
Zeng F, Zhang X 2014 Chin. Optics 7 731
[19] 彭飞, 张攀, 杨德兴, 康明武, 马百恒 2015 光子学报 44 22
Peng F, Zhang P, Yang D X, Kang M W, Ma B H 2015 Acta Photon. Sin. 44 22
[20] 丁意桐, 高震宇, 彭旭, 宋凝芳, 冯迪, 赵东峰, 迟小羽 2020 激光与光电子学进展 57 130801
Ding Y T, Gao Z Y, Peng X, Song N F, Feng D, Zhao D F, Chi X Y 2020 Laser & Optoelectronics Progress 57 130801
[21] 尚万里, 杨家敏, 赵阳, 朱托, 熊刚 2011 60 094212
Google Scholar
Shang W L, Yang J M, Zhao Y, Zhu T, Xiong G 2011 Acta Phys. Sin. 60 094212
Google Scholar
[22] 刘全, 吴建宏, 郭培亮, 陈新华 2019 中国激光 46 0313001
Google Scholar
Liu Q, Wu J H, Guo P L, Chen X H 2019 Chin. J. Lasers 46 0313001
Google Scholar
[23] 邬融, 田玉婷, 赵东峰, 李大为, 华能, 邵平 2016 65 054202
Google Scholar
Wu R, Tian Y T, Zhao D F, Li D W, Hua N, Shao P 2016 Acta Phys. Sin. 65 054202
Google Scholar
-
图 1 波导使用不同衍射级次耦入的简示图
Fig. 1. Schematic diagram of waveguide coupling using different diffraction orders.
图 2 左右微投发光经波导耦合输出到人眼, 重叠视场正好为0的理想情况
Fig. 2. The left and right micro-projector output light to the human eye by waveguide, where the overlapping field of view is exactly 0
图 3 单微投θavg = FOV/2时, 衍射波导支持的最大FOV角度与折射率关系
Fig. 3. Relationship between the maximum FOV and the refractive index when θavg = FOV/2.
图 4 单微投θavg = FOV/2时 (a) 固定q = 1.3, 单光栅支持多色光波导的FOV角度随n变化曲线; (b)固定n = 1.75, 单光栅支持多色光波导的FOV角度随q变化曲线
Fig. 4. When θavg = FOV/2: (a) q = 1.3, the relation curve between multi-color FOV and n supported by single grating; (b) n = 1.75, the relation curve between multi-color FOV and q.
图 5 衍射波导的光线传输以及全反级次视场标记
Fig. 5. Light transmission of diffraction waveguide and FOV marker of TIR.
图 7 (a)各角度光线在光栅区的全内反射次数; (b)微投在x方向归一化光能的投射曲线
Fig. 7. (a) Number of TIR at various incident angles in the grating area; (b) required projection curve of micro-projecter normalized light energy along the x direction.
图 8 (a) 微投在x方向归一化光能的投射曲线; (b) 按(a)图对投射端优化后的重新计算结果
Fig. 8. (a) Required projected angular light energy distribution function along the x direction; (b) recalculated results after optimizing the projection by (a).
图 9 (a) 微投在x方向RGB三色光随FOV归一化光能的投射曲线; (b) 按(a)图对投射端优化后的重新计算结果
Fig. 9. (a) Required projected angular light energy distribution function of RGB along the x direction; (b) recalculated results after optimizing the projection by (a).
图 10 (a) 微投在x方向GB两色光随视场角度归一化光能的投射曲线; (b) 按(a)图对投射端优化后的重新计算结果
Fig. 10. (a) Required projected angular light energy distribution function of GB along the x direction; (b) recalculated results after optimizing the projection by (a).
表 1 不同中心光线角和波导介质折射率支持耦入的最大FOV
Table 1. Support maximum FOV by different configurations.
中心光
线角/(°)介质折
射率nFOVmax/(°) 介质折
射率nFOVmax/(°) 10 1.5 29.41 1.75 44.76 15 1.5 30.00 1.75 45.68 20 1.5 30.85 1.75 47.03 25 1.5 32.02 1.75 48.88 30 1.5 33.55 1.75 51.31 
下载: 导出CSV
-
[1] Miller J M, Beaucoudrey N, Chavel P, Turunen J, Cambril E 1997 Appl. Opt. 36 5717
Google Scholar
[2] Kimmel J, Levola T, Saarikko P, et al. 2008 JSID 16 351
Google Scholar
[3] Jagt H J B, Cornelissen H J, Bastiaansen C W M, Broer D J 2004 Adv. Mater. 16 2108
Google Scholar
[4] 周忠, 周颐, 肖江剑 2015 中国科学: 信息科学 45 157
Google Scholar
Zhou Z, Zhou Y, Xiao J J 2015 Sci.Sin. Info. 45 157
Google Scholar
[5] Chen H W, Weng Y S, Xu D M, Tabiryan N V, Wu S T 2016 Opt. Express 24 7287
Google Scholar
[6] 高源, 刘越, 程德文, 王涌天 2016 计算机辅助设计与图形学学报 28 896
Google Scholar
Gao Y, Liu Y, Cheng D W, Wang Y T 2016 J. of Computer-Aided Design & Computer Graphics 28 896
Google Scholar
[7] Lalanne P 1999 J. Opt. Soc. Am. A 16 2517
Google Scholar
[8] Saarikko P 2008 Proc. SPIE 7001 700105
Google Scholar
[9] 梁华伟, 石顺祥, 李家立 2007 56 2293
Google Scholar
Liang H W, Shi S X, Li J L 2007 Acta Phys. Sin. 56 2293
Google Scholar
[10] Liu Z Y, Pang Y J, Pan C, Huang Z H 2017 Opt. Express 25 30720
Google Scholar
[11] Levola T, Laakkonen P 2007 Opt. Express 15 2067
Google Scholar
[12] Amitai Y, Reinhom S, Friesem A A 1995 Appl. Opt. 34 1352
Google Scholar
[13] Levola T 2006 JSID 14 467
Google Scholar
[14] Kress B C 2019 Proc. SPIE 11062 110620J-1
[15] Zhang N N, Liu J, Han J, LI X, Yang F, Wang X, Hu B, Wang Y T 2015 Appl. Opt. 54 3645
Google Scholar
[16] 刘辉 2012 硕士学位论文 (杭州: 浙江大学)
Liu H 2012 M. S. Dissertation (Hangzhou: Zhejiang University) (in Chinese)
[17] Guo J J, Tu Y, Yang L L, Wang L L 2015 Opt. Engineering 54 232
[18] 曾飞, 张新 2014 中国光学 7 731
Zeng F, Zhang X 2014 Chin. Optics 7 731
[19] 彭飞, 张攀, 杨德兴, 康明武, 马百恒 2015 光子学报 44 22
Peng F, Zhang P, Yang D X, Kang M W, Ma B H 2015 Acta Photon. Sin. 44 22
[20] 丁意桐, 高震宇, 彭旭, 宋凝芳, 冯迪, 赵东峰, 迟小羽 2020 激光与光电子学进展 57 130801
Ding Y T, Gao Z Y, Peng X, Song N F, Feng D, Zhao D F, Chi X Y 2020 Laser & Optoelectronics Progress 57 130801
[21] 尚万里, 杨家敏, 赵阳, 朱托, 熊刚 2011 60 094212
Google Scholar
Shang W L, Yang J M, Zhao Y, Zhu T, Xiong G 2011 Acta Phys. Sin. 60 094212
Google Scholar
[22] 刘全, 吴建宏, 郭培亮, 陈新华 2019 中国激光 46 0313001
Google Scholar
Liu Q, Wu J H, Guo P L, Chen X H 2019 Chin. J. Lasers 46 0313001
Google Scholar
[23] 邬融, 田玉婷, 赵东峰, 李大为, 华能, 邵平 2016 65 054202
Google Scholar
Wu R, Tian Y T, Zhao D F, Li D W, Hua N, Shao P 2016 Acta Phys. Sin. 65 054202
Google Scholar
下载:
计量
- 文章访问数: 8254
- PDF下载量: 208
- 被引次数: 0
