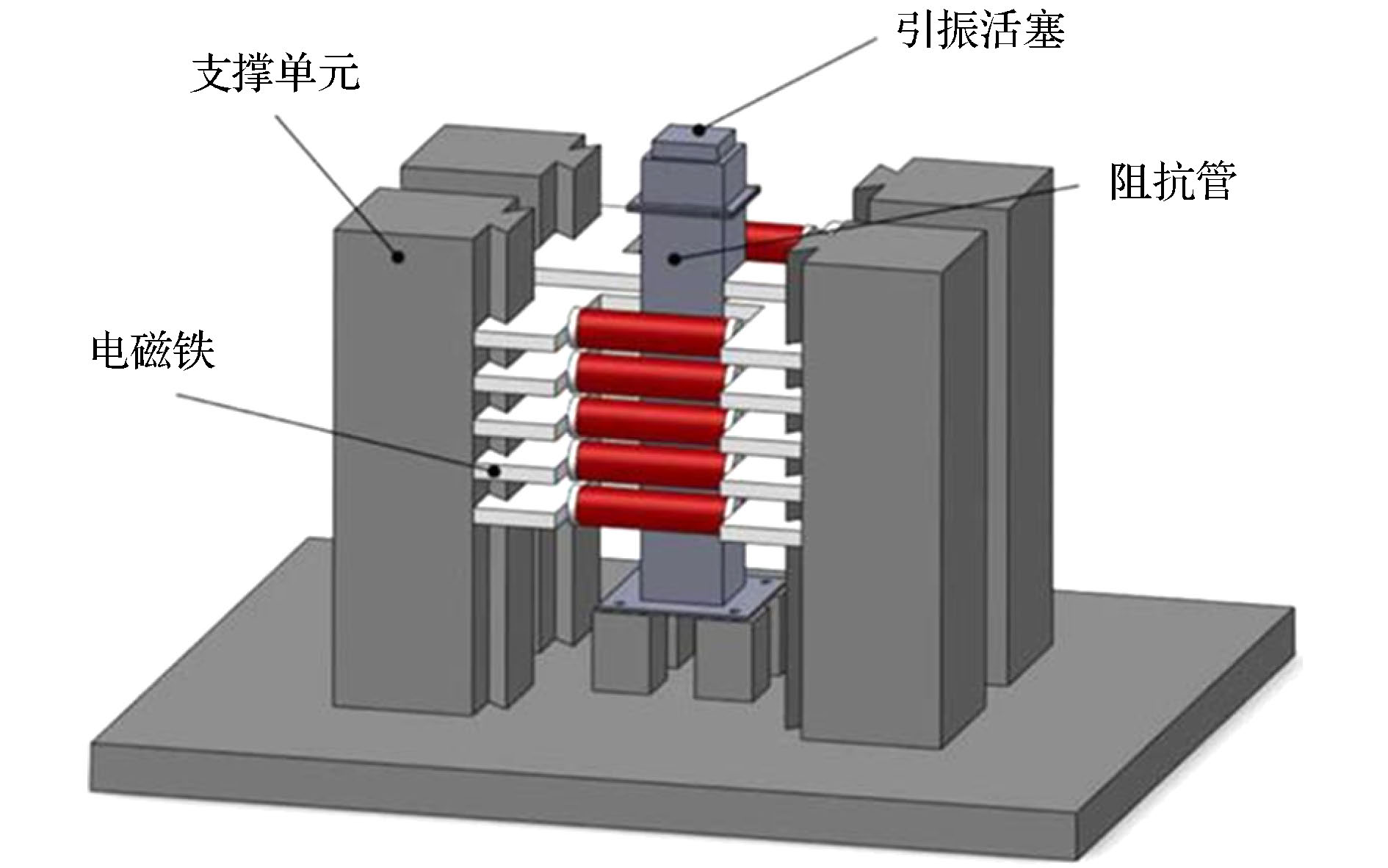
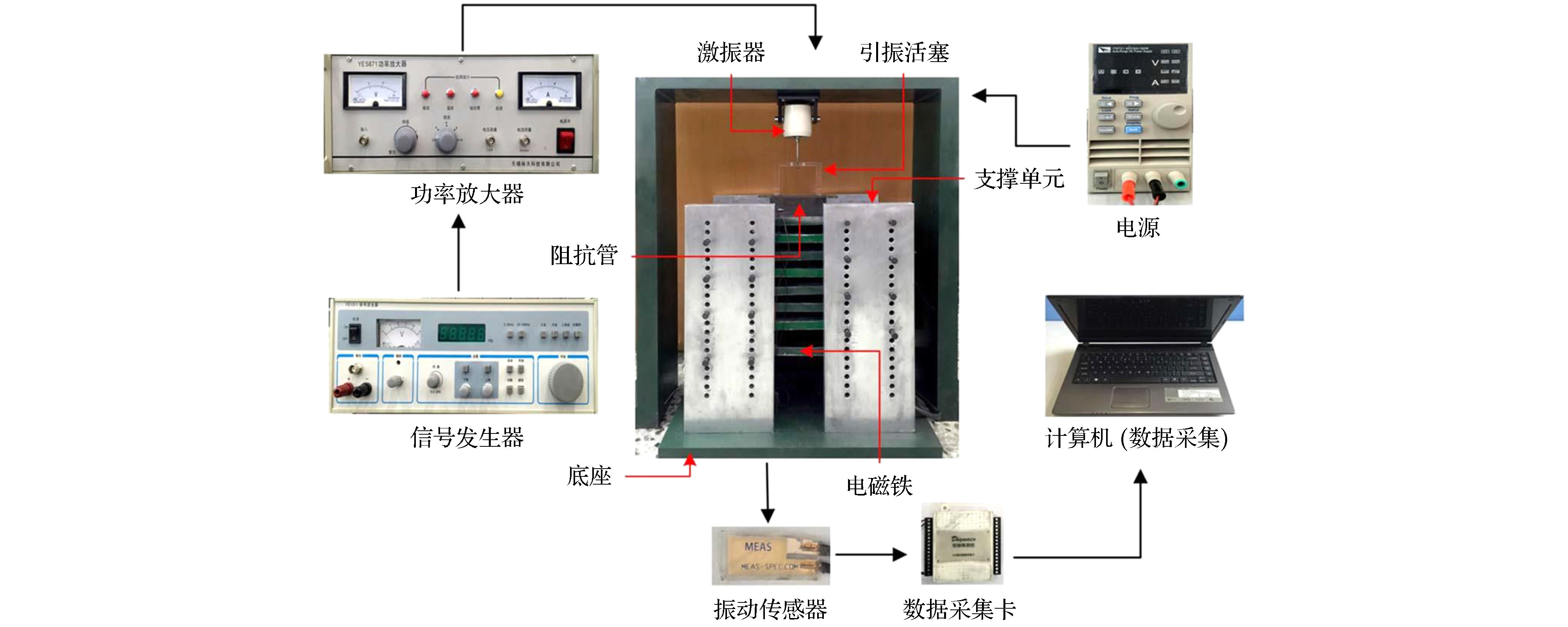
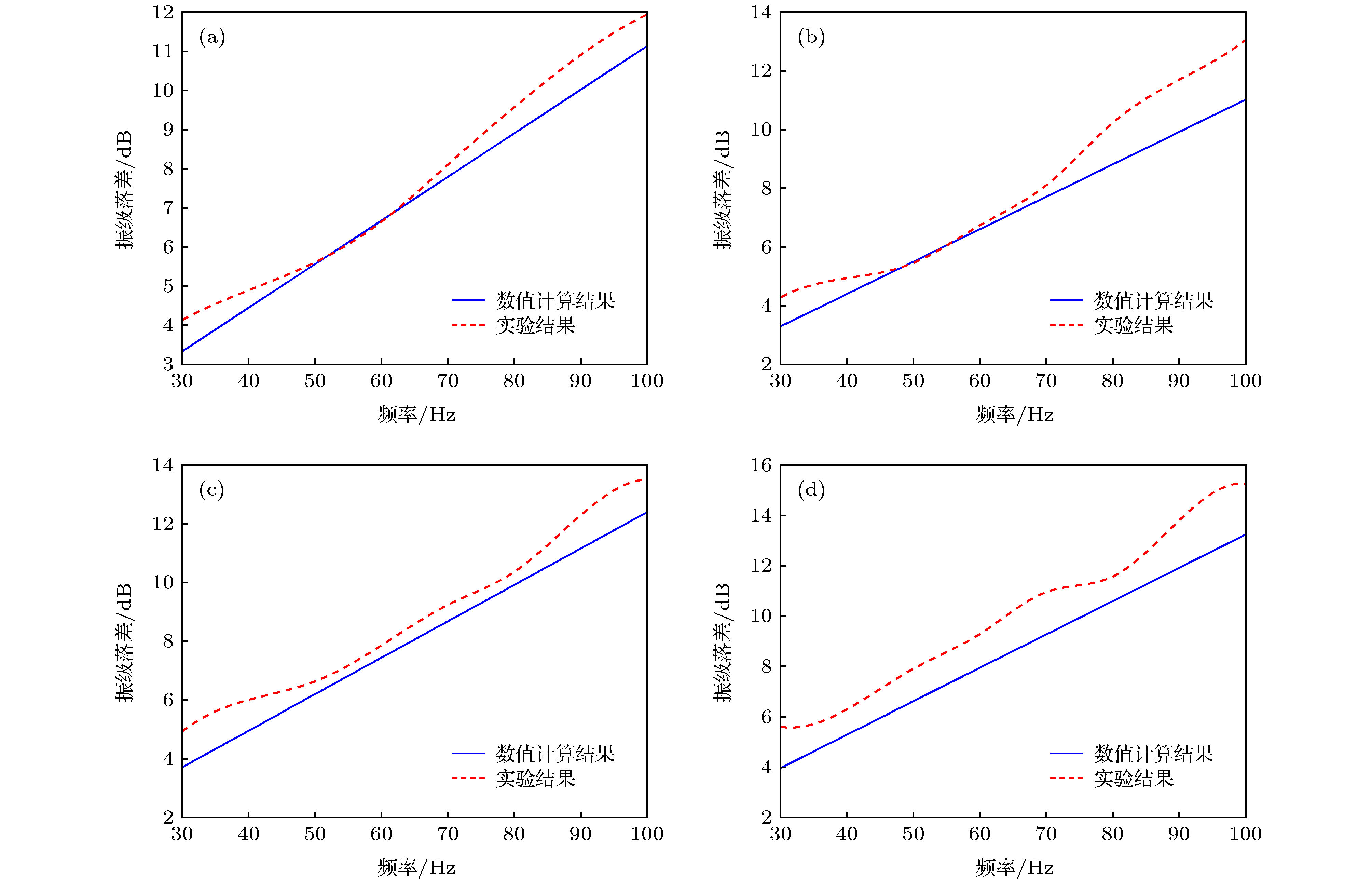
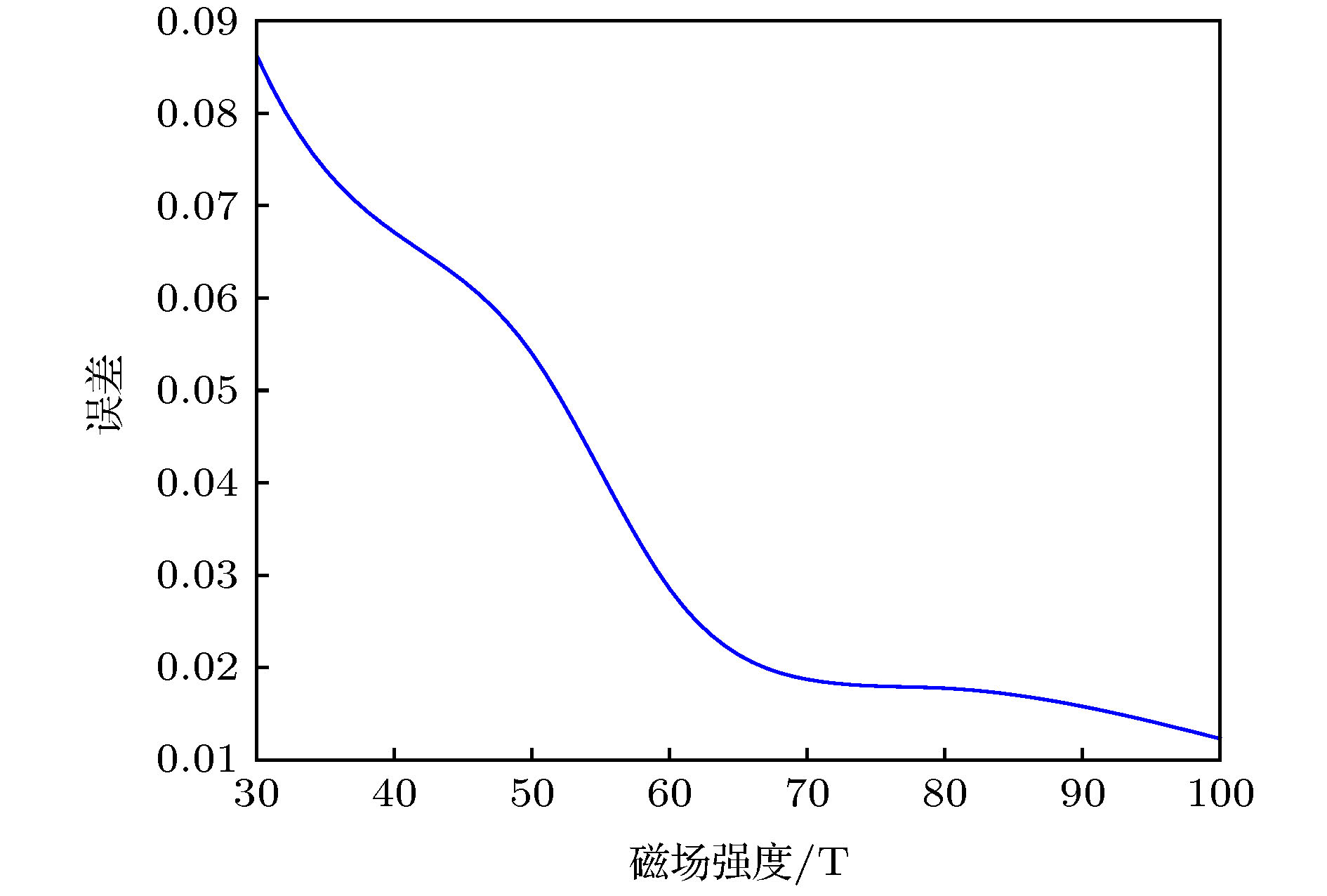
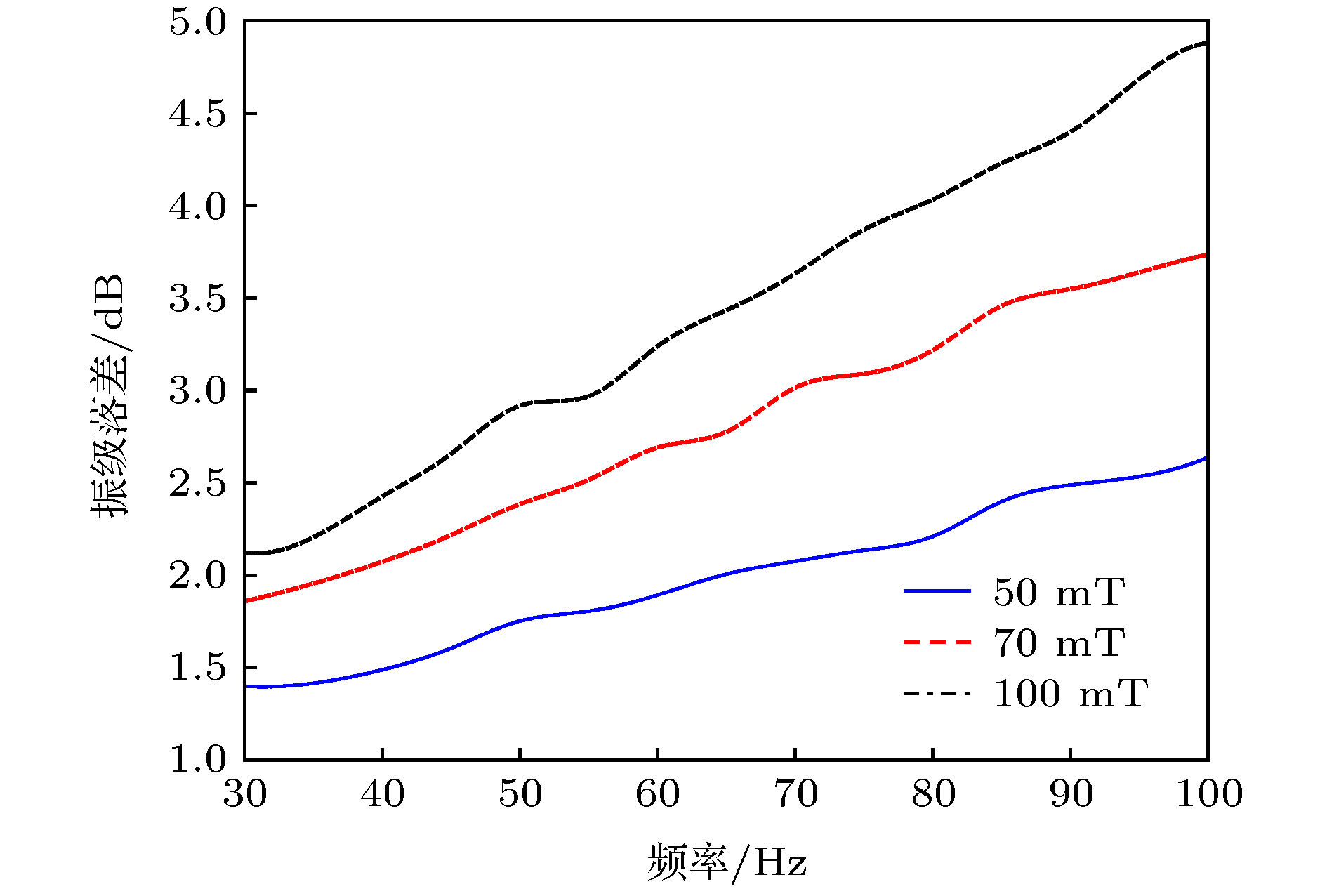
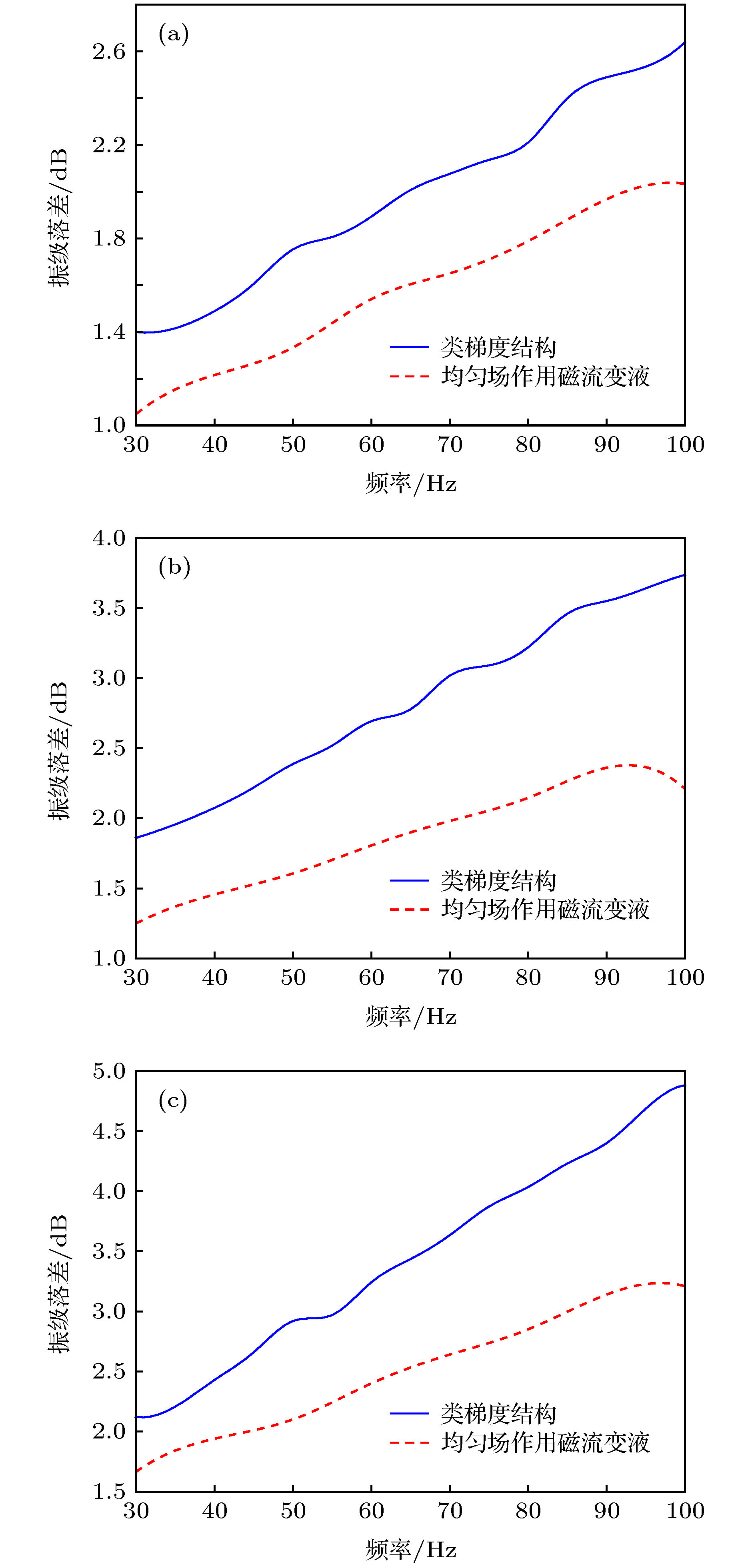
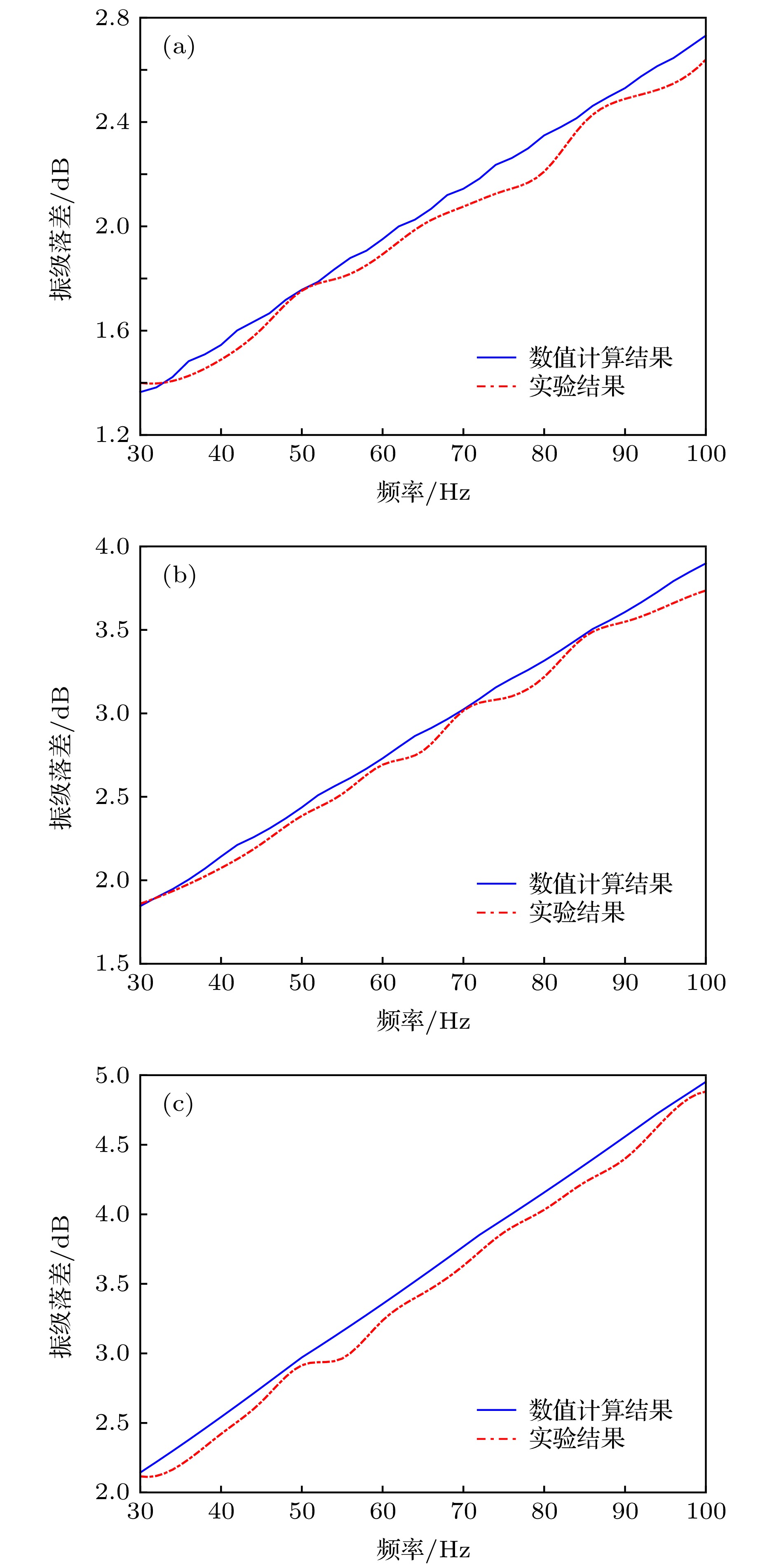
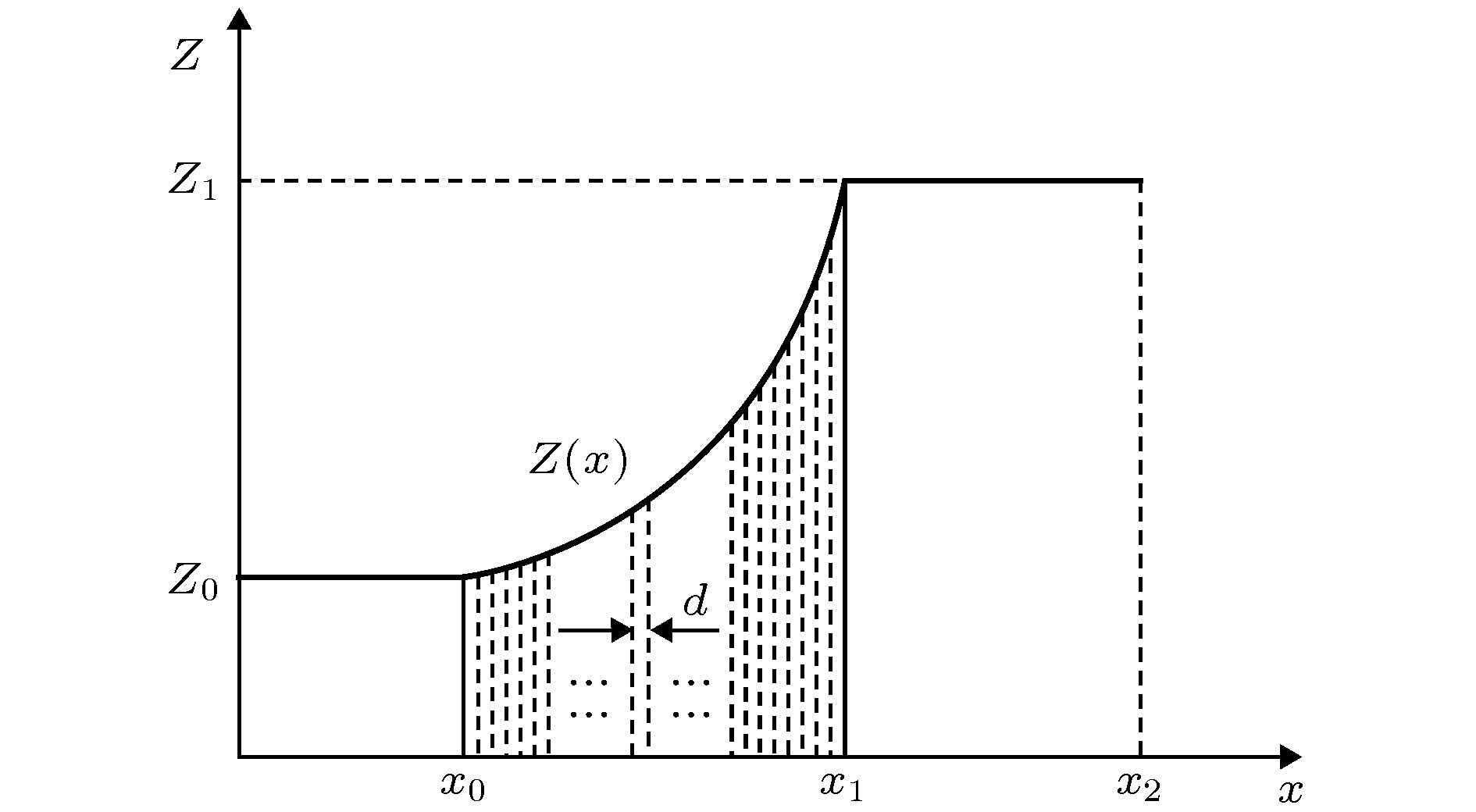
-
提出了一种磁流变液构成的类梯度结构, 并通过理论建模、数值计算和实验研究了该结构的振动传递特性. 磁流变液在磁场作用下具有液固转换的特殊理化性质, 而液固转换过程就是磁流变液的振动传递阻抗变化过程. 因此, 基于磁流变液的这一特性, 通过控制磁场, 构建了类梯度结构. 基于弹性波传递的一维波动方程, 建立了垂直入射的弹性波在类梯度结构中传递的波动方程. 然后, 使用连续介质的离散化方法和传递矩阵法进行求解, 得到振级落差的表达式, 对其进行数值计算, 分析类梯度结构的振级落差随弹性波频率和磁场强度的变化趋势. 最后, 对类梯度结构的振动传递特性进行了实验研究, 分析了磁场强度对类梯度结构振动传递特性的影响. 研究结果表明, 与均匀场作用的磁流变液相比, 类梯度结构对弹性波的衰减效果更好, 且该结构具备良好的可调控特性.In this paper, a gradient-like structure composed of magnetorheological (MR) fluids is proposed, and its vibration transfer characteristic is studied through the modeling, numerical calculation and experimental test. Under the action of an externally applied magnetic field, the MR fluid exhibits the liquid-solid transformation property: the process of transformation between solid and liquid in fact is the change of vibration-transfer impedance. Therefore, based on this property, the gradient-like structure is constructed by controlling the external magnetic field. Based on the wave equation of one-dimensional elastic wave propagation, the wave equation of elastic wave transfer in the gradient-like structure is established. In order to describe the relationship between the complex shear modulus and Lame constant of MR fluid and magnetic field intensity in the wave equation, the equivalent parameter model of MR fluid is established based on the theory of elasticity and viscoelastic materials. Then, the experimental set-up is built to modify this model through experiments. Afterward, the discretization method of continuous medium and transfer matrix method are adopted to solve the wave equation, and the expression of vibration level drop is obtained. Through the numerical calculation, the trend of vibration level drop varying with the frequency of incident elastic wave and the intensity of magnetic field for the gradient-like structure is obtained. Finally, the vibration transfer characteristic of the gradient-like structure is studied experimentally, and the influence of magnetic field intensity on the vibration transfer characteristic of the gradient-like structure is analyzed. The results show that the numerical results are in good accordance with the experimental results, thereby verifying that the numerical model is accurate. And the gradient-like structure has a better attenuation effect on the elastic wave than the MR fluid under the action of a uniform magnetic field, and has an excellent tunable property as well.
-
Keywords:
- magnetorheological fluid /
- gradient-like structure /
- elastic wave transfer /
- vibration level drop
[1] Ghaffari A, Hashemabadi S H, Ashtiani M 2015 J. Intell. Mater. Syst. Struct. 26 881
Google Scholar
[2] Ashour O, Rogers C, Kordonsky W 2016 J. Intell. Mater. Syst. Struct. 7 123
Google Scholar
[3] Esmaeilnezhad E, Hajiabadi S H, Choi H J 2019 J. Ind. Eng. Chem. 80 197
Google Scholar
[4] Rabinow J 1948 T-AIEE. 67 1308
Google Scholar
[5] Hui L X, Zhang H, Li G X, Yan Y X, Meng S 2016 Optoelectron. Adv. Mater. Rapid Commun. 10 74
[6] Ding Y, Zhang L, Zhu H T, Li Z X 2013 Smart Mater. Struct. 22 115003
Google Scholar
[7] 张雅娴, 沈景凤, 徐斌 2017 电子科技 30 170
Google Scholar
Zhang Y X, Shen J F, Xu B 2017 Elect. Sci. Technol. 30 170
Google Scholar
[8] Liu S G, Feng L F, Zhao D, Shi X X, Zhang Y P, Jiang J X, Zhao Y C, Zhang C J, Chen L 2019 Smart Mater. Struct. 28 085037
Google Scholar
[9] Jozefczak A 2003 J. Magn. Magn. Mater. 256 267
Google Scholar
[10] Jozefczak A, Skumiel A, Labowski M 2003 J. Magn. Magn. Mater. 258 474
Google Scholar
[11] Bramantya M A, Sawada T 2011 J. Magn. Magn. Mater. 323 1330
Google Scholar
[12] Bramantya M A, Motozawa M, Sawada T 2010 J. Phys. Condes. Matter 22 2283
Google Scholar
[13] Bramantya M A, Motozawa M, Takuma H, Faiz M, Sawada T 2009 11th Conference on Electrorheological Fluids and Magnetorheological Suspensions Dresden, Germany, August 25—29, 2008 p012040
[14] Lee J H, Kim J, Kim H J 2001 J. Acoust. Soc. Am. 110 2282
Google Scholar
[15] Mahjoob M J, Mohammadi N, Malakooti S 2012 Appl. Acoust. 73 614
Google Scholar
[16] Rodríguez-López J, Elvira L, Resa P, de Espinosa F M 2013 J. Phys. D: Appl. Phys. 46 065001
Google Scholar
[17] 文娟, 廖昌荣, 赵慧婷, 唐锐, 张登友 2014 功能材料 45 10148
Google Scholar
Wen J, Liao C R, Zhao H T, Tang R, Zhang D Y 2014 Funct. Mater. 45 10148
Google Scholar
[18] Liu S G, Shi X X, Zhao D, Chen L, Feng L F, Zhang Z Y 2018 Smart Mater. Struct. 27 115016
Google Scholar
[19] Zhao D, Shi X X, Liu S G, Wang F H 2020 J. Intell. Mater. Syst. Struct. 31 882
Google Scholar
[20] Hasheminejad S M, Maleki M 2006 Ultrasonics. 45 165
Google Scholar
[21] 杨德森, 孙玉, 胡博, 韩闯, 靳仕源 2014 哈尔滨工程大学学报 35 1458
Google Scholar
Yang D S, Sun Y, Hu B, Han C, Jin S Y 2014 J. Harbin. Eng. Univ. 35 1458
Google Scholar
[22] Sun Q, Zhou J X, Zhang L 2003 J. Sound Vibr. 261 465
Google Scholar
-
图 2 磁流变液构成的类梯度结构示意图
Fig. 2. Schematic diagram of the experimental device for constructing gradient-like structure.
图 3 匀质类固态磁流变液的振动传递特性
Fig. 3. Vibration transfer characteristic of the homogeneous quasi-solid magnetorheological fluid.
图 5 不同磁场强度下的类固态磁流变液的振动传递特性对比 (a) 30 mT; (b) 50 mT; (c) 70 mT; (d) 100 mT
Fig. 5. Comparison of vibration transfer characteristic of quasi-solid magnetorheological fluid under different magnetic field: (a) 30 mT; (b) 50 mT; (c) 70 mT; (d) 100 mT.
图 6 理论结果和实验结果之间的误差
Fig. 6. Error between theoretical results and experimental results.
图 8 不同磁场强度作用下类梯度结构的振动传递特性
Fig. 8. Vibration characteristic of the gradient-like structure under different magnetic field intensity.
图 9 类梯度结构与均匀场作用磁流变液对比图 (a) 50 mT; (b) 70 mT; (c) 100 mT
Fig. 9. Comparison between gradient-like structure and homogeneous magnetorheological fluid: (a) 50 mT; (b) 70 mT; (c) 100 mT
图 10 类梯度结构振动传递特性的实验与理论对比图 (a) 50 mT; (b) 70 mT; (c) 100 mT
Fig. 10. Comparison between experimental and numerical results of vibration transfer characteristic of gradient like structure: (a) 50 mT; (b) 70 mT; (c) 100 mT
表 1 磁流变液性能参数
Table 1. Characteristic parameters of the magnetorheological fluid.
性能名称 平均粒径 颗粒密度 载液密度 零场黏度 颗粒体积分数 d/μm ${\rho _{\rm{f}}}$/kg·m–3 ${\rho _{\rm{r}}}$/kg·m–3 $\eta $/Ns·m–2 $\theta $ 参数值 5.5 6698 998 0.2425 27% 
下载: 导出CSV
表 2 修正后的理论模型和实验结果对比
Table 2. Comparison of numerical results and experimental results.
修正倍数 振级落差 理论值/dB 实验值/dB 误差 2倍 9.6876 15.4419 37.31% 5倍 14.4739 6.27% 10倍 18.2995 18.51% 15倍 19.8275 28.40% 20倍 20.7795 34.57%
下载: 导出CSV
表 3 修正后的理论模型和实验结果对比(5—10倍)
Table 3. Comparison of numerical results and experimental results (5–10 times).
修正倍数 振级落差 理论值/dB 实验值/dB 误差 5倍 14.4739 15.4419 6.27% 6倍 15.5312 0.58% 7倍 16.4132 6.29% 8倍 17.1524 11.08% 9倍 17.7743 15.10%
下载: 导出CSV
表 4 修正后的理论模型和实验结果对比(30—100 Hz)
Table 4. Comparison of numerical results and experimental results (30–100 Hz).
输入弹性波频率 振级落差 理论值/dB 实验值/dB 误差 30 Hz 5.1457 5.6042 8.18% 40 Hz 6.8610 6.7979 0.93% 50 Hz 8.5762 8.5199 0.66% 60 Hz 10.2915 10.2858 0.06% 70 Hz 12.0067 11.5679 4.3% 80 Hz 13.7219 12.8765 6.51% 90 Hz 14.4372 13.8086 4.55% 100 Hz 15.5312 15.4419 0.58%
下载: 导出CSV
表 5 实验与理论结果误差
Table 5. Error between experimental and theoretical results.
编号 实验参数/mT 误差 实验1 50 2.856% 实验2 70 2.233% 实验3 100 3.585%
下载: 导出CSV
-
[1] Ghaffari A, Hashemabadi S H, Ashtiani M 2015 J. Intell. Mater. Syst. Struct. 26 881
Google Scholar
[2] Ashour O, Rogers C, Kordonsky W 2016 J. Intell. Mater. Syst. Struct. 7 123
Google Scholar
[3] Esmaeilnezhad E, Hajiabadi S H, Choi H J 2019 J. Ind. Eng. Chem. 80 197
Google Scholar
[4] Rabinow J 1948 T-AIEE. 67 1308
Google Scholar
[5] Hui L X, Zhang H, Li G X, Yan Y X, Meng S 2016 Optoelectron. Adv. Mater. Rapid Commun. 10 74
[6] Ding Y, Zhang L, Zhu H T, Li Z X 2013 Smart Mater. Struct. 22 115003
Google Scholar
[7] 张雅娴, 沈景凤, 徐斌 2017 电子科技 30 170
Google Scholar
Zhang Y X, Shen J F, Xu B 2017 Elect. Sci. Technol. 30 170
Google Scholar
[8] Liu S G, Feng L F, Zhao D, Shi X X, Zhang Y P, Jiang J X, Zhao Y C, Zhang C J, Chen L 2019 Smart Mater. Struct. 28 085037
Google Scholar
[9] Jozefczak A 2003 J. Magn. Magn. Mater. 256 267
Google Scholar
[10] Jozefczak A, Skumiel A, Labowski M 2003 J. Magn. Magn. Mater. 258 474
Google Scholar
[11] Bramantya M A, Sawada T 2011 J. Magn. Magn. Mater. 323 1330
Google Scholar
[12] Bramantya M A, Motozawa M, Sawada T 2010 J. Phys. Condes. Matter 22 2283
Google Scholar
[13] Bramantya M A, Motozawa M, Takuma H, Faiz M, Sawada T 2009 11th Conference on Electrorheological Fluids and Magnetorheological Suspensions Dresden, Germany, August 25—29, 2008 p012040
[14] Lee J H, Kim J, Kim H J 2001 J. Acoust. Soc. Am. 110 2282
Google Scholar
[15] Mahjoob M J, Mohammadi N, Malakooti S 2012 Appl. Acoust. 73 614
Google Scholar
[16] Rodríguez-López J, Elvira L, Resa P, de Espinosa F M 2013 J. Phys. D: Appl. Phys. 46 065001
Google Scholar
[17] 文娟, 廖昌荣, 赵慧婷, 唐锐, 张登友 2014 功能材料 45 10148
Google Scholar
Wen J, Liao C R, Zhao H T, Tang R, Zhang D Y 2014 Funct. Mater. 45 10148
Google Scholar
[18] Liu S G, Shi X X, Zhao D, Chen L, Feng L F, Zhang Z Y 2018 Smart Mater. Struct. 27 115016
Google Scholar
[19] Zhao D, Shi X X, Liu S G, Wang F H 2020 J. Intell. Mater. Syst. Struct. 31 882
Google Scholar
[20] Hasheminejad S M, Maleki M 2006 Ultrasonics. 45 165
Google Scholar
[21] 杨德森, 孙玉, 胡博, 韩闯, 靳仕源 2014 哈尔滨工程大学学报 35 1458
Google Scholar
Yang D S, Sun Y, Hu B, Han C, Jin S Y 2014 J. Harbin. Eng. Univ. 35 1458
Google Scholar
[22] Sun Q, Zhou J X, Zhang L 2003 J. Sound Vibr. 261 465
Google Scholar
下载:
计量
- 文章访问数: 7906
- PDF下载量: 102
- 被引次数: 0
