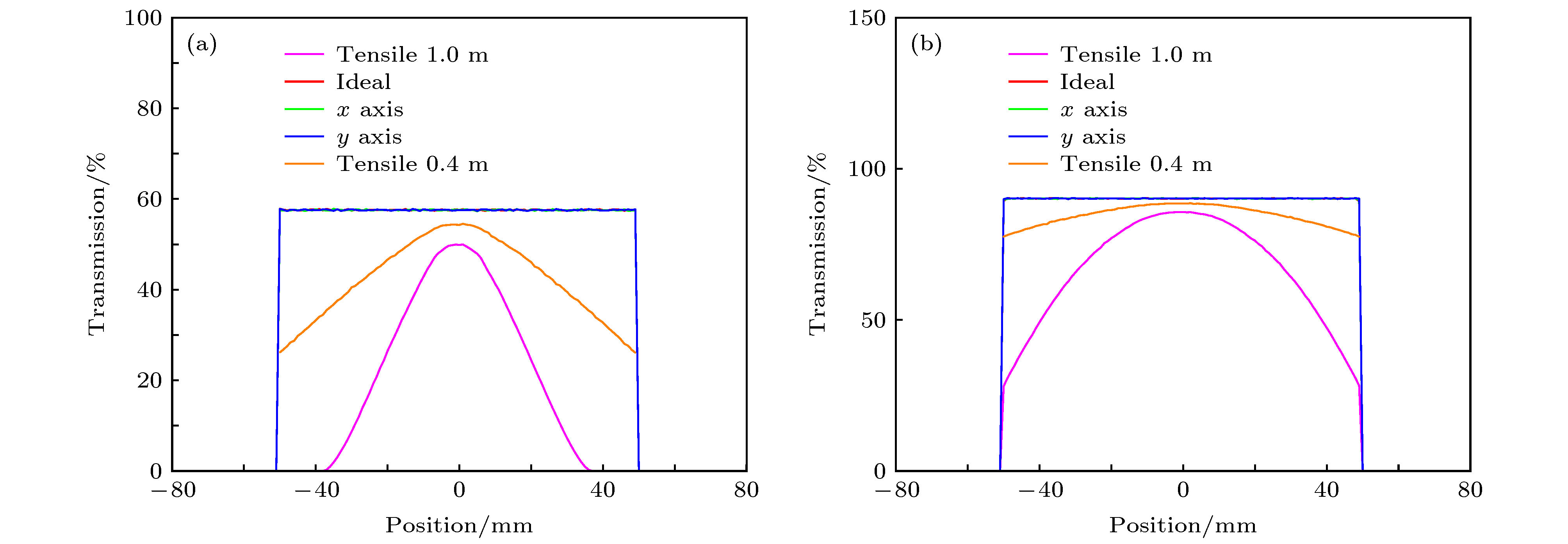
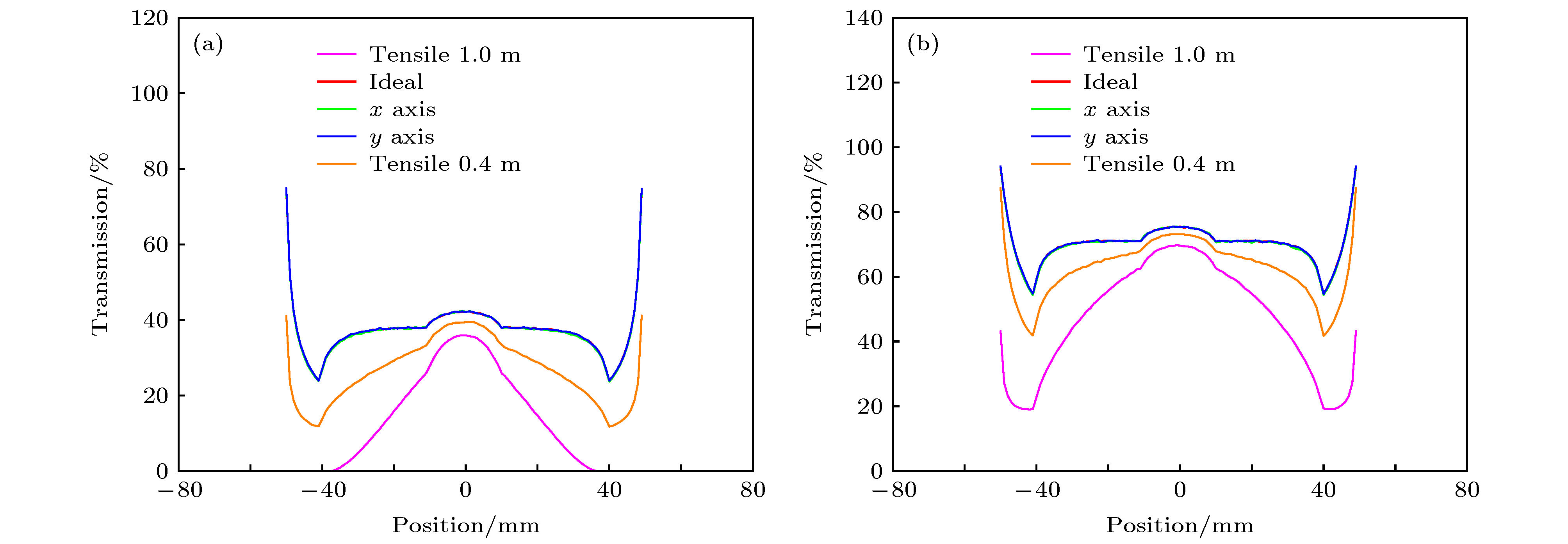
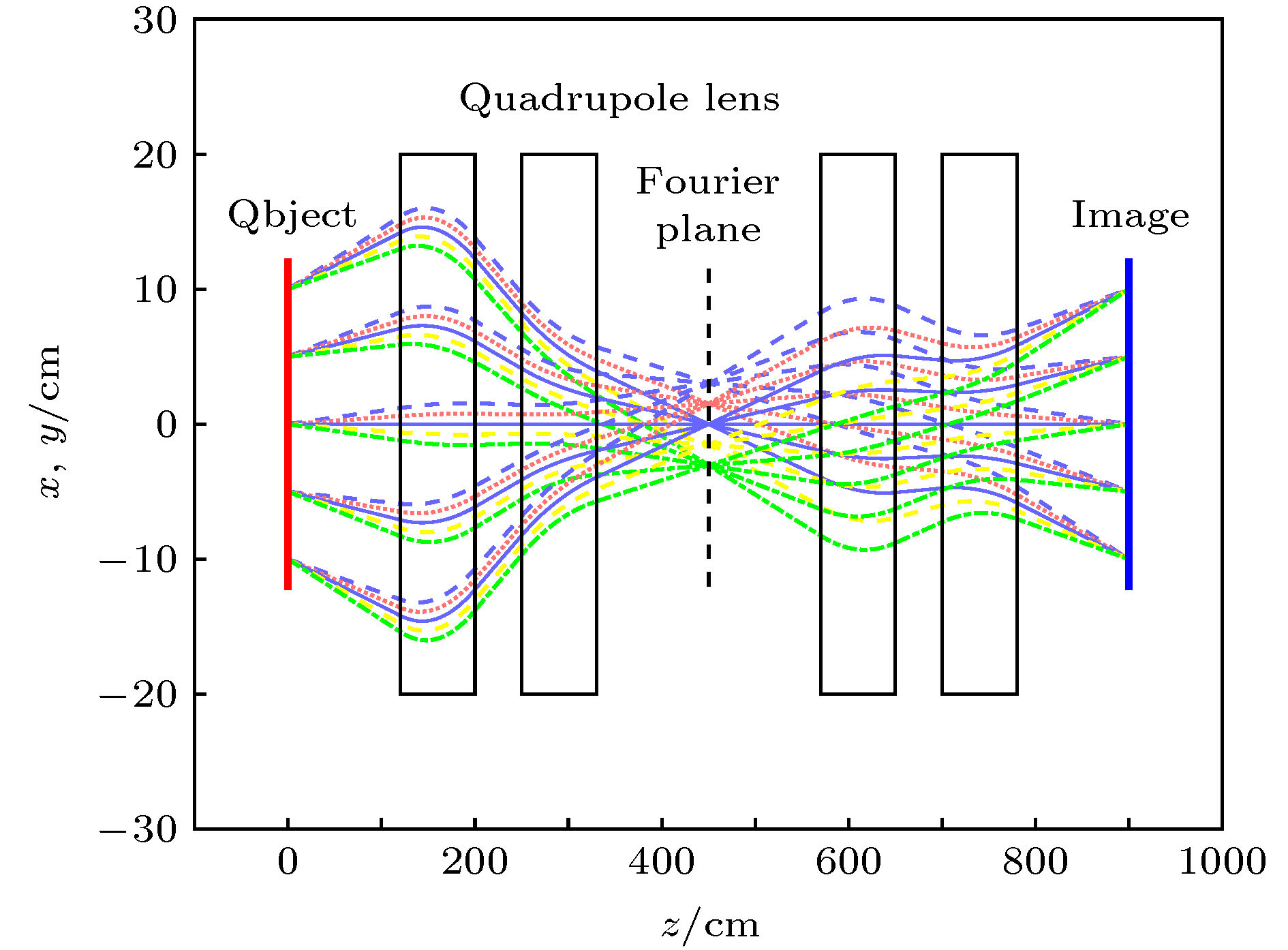
-
角度准直器在高能质子照相中有着重要作用, 既可以利用准直器提高图像对比度, 又能通过二次成像实现材料诊断及密度重建, 因此减小通过准直器后通量值的误差具有重要意义. 本文通过理论分析, 提出了一种高能质子照相中准直器设计的方法, 通过Geant4程序建立了1.6 GeV的质子成像系统, 该系统分别使用理想准直器、拉伸型准直器和利用该方法设计的准直器, 并对比通过客体后的通量分布. 结果表明, 在使用理想准直器和该方法设计的角度准直器时, 二者得到的客体的通量分布符合较好, 而使用拉伸型准直器时, 与使用理想准直器得到的结果相差较大. 因此利用理想准直器方法设计的准直器可以很好地减小通量误差.The angle-cut collimator plays an important role in high-energy proton radiography. By using the collimator, the image contrast can be improved, and the material diagnosis and density reconstruction can be realized through secondary imaging. As all these techniques depend on the flux value, it is of great significance to reduce the error of the detected flux value. The ideal collimator is a much thin surface, but thick enough to block protons outside the collimation region. It is designed by stretching the aperture of the collimation plane. The shape is cylindrical, and it will increase the error of the flux value with the angle truncation. The initial bunch is defined and the phase diagram of the bunch within the angle-cut is ideal in the theoretical model. The equation of designing the collimator is given by theoretical analysis. It is given by the transfer matrix, the radius of the object and the angle-cut. The pore structure is oval-shaped by calculating and simulating. The proton imaging system of 1.6 GeV is established by Geant4 program, and the detector is ideal. The round copper plate and the concentric spheres are chosen as objects respectively. The parameters of the designed collimator is given by this method. The ideal collimator, tensile collimator and designed collimator are used in simulation, the radius of object is 5 cm and the angle-cut is 2 mrad and 3.5 mrad. The results show that when using the ideal and the designed angle-cut collimator, the flux distributions are in good agreement, while when using the tensile collimator, the result is quite different from that obtained by using the ideal collimator. Therefore, the collimator designed by this method can effectively reduce the error of the detected flux value.
-
Keywords:
- high-energy proton radiography /
- angle-cut collimator /
- density reconstruction /
- Geant4 code
[1] Gavton A, Morris C L, Ziock H J, et al. 1996 Los Alamos National Report 96 420
[2] Mottershead C T, Zumbro J D 1997 Proceedings of the 1997 Particle Accelerator Conference Vancouver B C, Canada, May 12–16, 1997 p1397
[3] Jason A J, Barlow D B, Blind B, Kelley J P, Lysenko W P, Neri F, Walstrom P L, Waynert J, Schulze M 2001 Proceedings of the 2001 Particle Accelerator Conference Chicago, USA, June 18–22, 2001 p3374
[4] King N S P, Ables E, Adams K, et al. 1999 Nucl. Instrum. Meth. Phys. Res., Sect. A 424 84
[5] Rigg P A, Schwartz C L, Hixson R S, Hogan G E, Kwiatkowski K K, Mariam F G, Marr-Lyon M, Merrill F E, Morris C L, Rightly P, Sauders A, Tupa D 2008 Phys. Rev. B 77 220101
Google Scholar
[6] Morris C L, Ables E, Alrick K R, et al. 2011 J. Appl. Phys. 109 104905
Google Scholar
[7] Antipov Y M, Afonin A G, Vasilevskii A V, et al. 2010 Instrum. Exp. Tech. 53 319
Google Scholar
[8] Golubev A A, Demidov V S, Demidova E V, Dudin S V, Kantsyrev A V, Kolesnikov S A, Mintsev V B, Smirnov G N, Turtikov V I, Utikin A V, Fortov V E, Sharkov B Y 2010 Tech. Phys. Lett. 36 177
Google Scholar
[9] Varentsov D, Antonov O, Bakhmutova A, et al. 2016 Rev. Sci. Instrum. 87 023303
Google Scholar
[10] Yang J J, Zhen X, Wei S M, Lv Y L, Wang F, Zhang Y W, Wen L P, Liu J Y, Cai H R, Ge T, Zhang S P, Cao L, Zhang T J, Li Z G 2016 CYC2016 Proceedings of the 21 st International Conference on Cyclotrons and their Applications Zurich, Switzerland, September 11–16, 2016 p401
[11] Merrill F E 2015 Rev. Accel. Sci. Technol. 8 165
Google Scholar
[12] Sheng L N, Zhao Y T, Yang G J, Wei T 2014 Laser Part. Beams 32 651
Google Scholar
[13] Wei T, Yang G J, Li Y D, et al. 2014 Chin. Phys. C 38 087003
Google Scholar
[14] Aufderheide M B, Park H, Hartouni E P 1999 AIP Conference Proceedings Sydney, Australia, June 28–July 2, 1999 p497
[15] Zumbro J D, Acuff A, Bull J S, et al. 2005 Radiat. Prot. Dosim. 117 447
[16] Fesseha G, Mariam, John P 2011 2011 High-Energy-Proton Microscopy Workshop Summary Report New Mexico, USA, October 27–28, 2011 p54
[17] Antipov Y M, Afonin A G, Gusev I A, et al. 2013 At. Energ. 114 359
Google Scholar
[18] Varentsov D, Bogdanov A, Demidov V S 2013 Phys. Medica 29 208
Google Scholar
[19] Yan Y, Sheng L N, Huang Z W, et al. 2015 Laser Part. Beams 33 439
Google Scholar
[20] Kantsyrev A V, Skoblyakov A V, Bogdanov A V 2018 J. Phys.: Conf. Ser. 946 012019
Google Scholar
[21] Agostinelli S, Allison J, Amako K A, et al. 2003 Nucl. Instrum. Meth. Phys. Res. Sect. A 506 250
Google Scholar
[22] Allison J, Amako K, Apostolakis J, et al. 2006 IEEE Trans. Nucl. Sci. 53 270
Google Scholar
-
图 2 一定截断角以内的质子束团在通过准直空间时的形状变化 (a) z = 0 m; (b) z = 0.6 m; (c) z = 1.2 m; (d) z = 1.8 m; (e) z = 2.4 m
Fig. 2. Shape changed of proton bunch within certain angle-cuts as it passes through the collimation space: (a) z = 0 m; (b) z = 0.6 m; (c) z = 1.2 m; (d) z = 1.8 m; (e) z = 2.4 m.
图 4 截断角为2 mrad、客体尺寸为5 cm时的目标束团边界线
Fig. 4. Boundary lines of the target bunch when the angle-cut is 2 mrad and the object size is 5 cm.
图 5 端口处的孔径值随截断角的变化 (a)
$z = 20\;{\rm{cm}}$ ; (b)$z = 120\;{\rm{cm}}$ Fig. 5. Aperture size varies with the angle-cut at the ports: (a)
$z = 20\;{\rm{cm}}$ ; (b)$z = 120\;{\rm{cm}}$ .
图 6 准直器孔径的形状 (a) x-y平面; (b) y-z平面
Fig. 6. Shape of aperture of the collimator: (a) x-y plane; (b) y-z plane.
图 7 客体示意图 (a)铜板; (b)同心球体
Fig. 7. Diagram of the object: (a) The round copper plate; (b) the concentric spheres.
图 8 通过铜板的通量分布 (a)截断角为2 mrad; (b)截断角为3.5 mrad
Fig. 8. Flux distribution after passing the round copper plate: (a) Angle-cut of 2 mrad; (b) angle-cut of 3.5 mrad.
图 9 通过同心球的通量分布 (a)截断角为2 mrad; (b)截断角为3.5 mrad
Fig. 9. Flux distribution after passing the concentric spheres: (a) Angle-cut of 2 mrad; (b) angle-cut of 3.5 mrad.
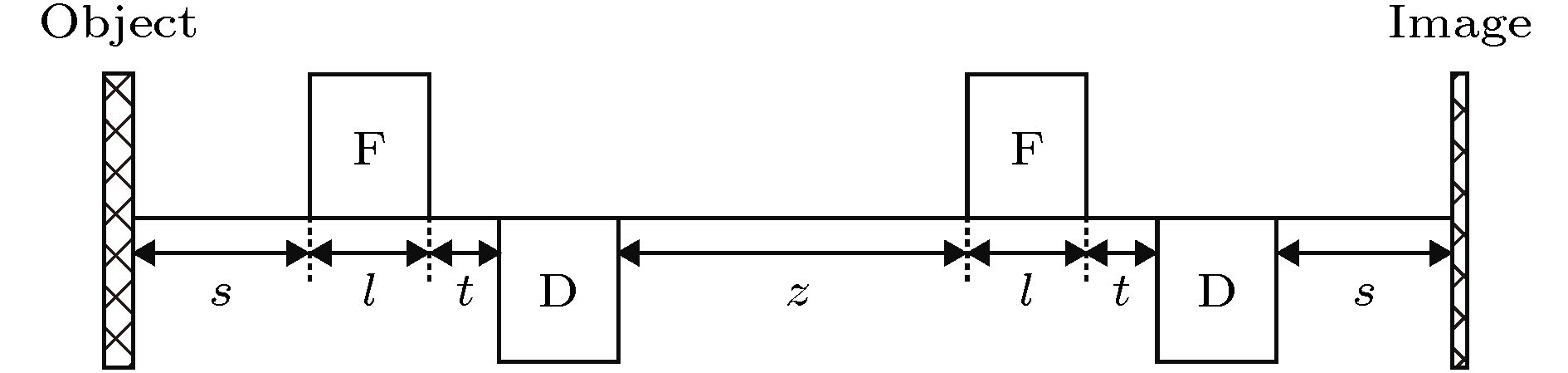
表 1 1.6 GeV质子成像系统参数
Table 1. Parameters of the proton radiography system of 1.6 GeV.
s/m l/m G/T·m–1 t/m 1.2 0.8 8.09 0.5 
下载: 导出CSV
表 2 准直器的孔径参数
Table 2. Aperture parameters of the collimator.
截断角/mrad 准直器类型 前端/cm 后端/cm 厚度/m 外半径/m 材料 x y x y 2 理想型 — 0.61 10–7 3 Al 拉伸型 0.61 0.61 1 & 0.4 3 W 设计型 2.04 2.46 0.61 1 3 W 3.5 理想型 — 1.07 10–7 3 Al 拉伸型 1.07 1.07 1 & 0.4 3 W 设计型 2.34 3.08 1.07 1 3 W
下载: 导出CSV
-
[1] Gavton A, Morris C L, Ziock H J, et al. 1996 Los Alamos National Report 96 420
[2] Mottershead C T, Zumbro J D 1997 Proceedings of the 1997 Particle Accelerator Conference Vancouver B C, Canada, May 12–16, 1997 p1397
[3] Jason A J, Barlow D B, Blind B, Kelley J P, Lysenko W P, Neri F, Walstrom P L, Waynert J, Schulze M 2001 Proceedings of the 2001 Particle Accelerator Conference Chicago, USA, June 18–22, 2001 p3374
[4] King N S P, Ables E, Adams K, et al. 1999 Nucl. Instrum. Meth. Phys. Res., Sect. A 424 84
[5] Rigg P A, Schwartz C L, Hixson R S, Hogan G E, Kwiatkowski K K, Mariam F G, Marr-Lyon M, Merrill F E, Morris C L, Rightly P, Sauders A, Tupa D 2008 Phys. Rev. B 77 220101
Google Scholar
[6] Morris C L, Ables E, Alrick K R, et al. 2011 J. Appl. Phys. 109 104905
Google Scholar
[7] Antipov Y M, Afonin A G, Vasilevskii A V, et al. 2010 Instrum. Exp. Tech. 53 319
Google Scholar
[8] Golubev A A, Demidov V S, Demidova E V, Dudin S V, Kantsyrev A V, Kolesnikov S A, Mintsev V B, Smirnov G N, Turtikov V I, Utikin A V, Fortov V E, Sharkov B Y 2010 Tech. Phys. Lett. 36 177
Google Scholar
[9] Varentsov D, Antonov O, Bakhmutova A, et al. 2016 Rev. Sci. Instrum. 87 023303
Google Scholar
[10] Yang J J, Zhen X, Wei S M, Lv Y L, Wang F, Zhang Y W, Wen L P, Liu J Y, Cai H R, Ge T, Zhang S P, Cao L, Zhang T J, Li Z G 2016 CYC2016 Proceedings of the 21 st International Conference on Cyclotrons and their Applications Zurich, Switzerland, September 11–16, 2016 p401
[11] Merrill F E 2015 Rev. Accel. Sci. Technol. 8 165
Google Scholar
[12] Sheng L N, Zhao Y T, Yang G J, Wei T 2014 Laser Part. Beams 32 651
Google Scholar
[13] Wei T, Yang G J, Li Y D, et al. 2014 Chin. Phys. C 38 087003
Google Scholar
[14] Aufderheide M B, Park H, Hartouni E P 1999 AIP Conference Proceedings Sydney, Australia, June 28–July 2, 1999 p497
[15] Zumbro J D, Acuff A, Bull J S, et al. 2005 Radiat. Prot. Dosim. 117 447
[16] Fesseha G, Mariam, John P 2011 2011 High-Energy-Proton Microscopy Workshop Summary Report New Mexico, USA, October 27–28, 2011 p54
[17] Antipov Y M, Afonin A G, Gusev I A, et al. 2013 At. Energ. 114 359
Google Scholar
[18] Varentsov D, Bogdanov A, Demidov V S 2013 Phys. Medica 29 208
Google Scholar
[19] Yan Y, Sheng L N, Huang Z W, et al. 2015 Laser Part. Beams 33 439
Google Scholar
[20] Kantsyrev A V, Skoblyakov A V, Bogdanov A V 2018 J. Phys.: Conf. Ser. 946 012019
Google Scholar
[21] Agostinelli S, Allison J, Amako K A, et al. 2003 Nucl. Instrum. Meth. Phys. Res. Sect. A 506 250
Google Scholar
[22] Allison J, Amako K, Apostolakis J, et al. 2006 IEEE Trans. Nucl. Sci. 53 270
Google Scholar
下载:
计量
- 文章访问数: 7050
- PDF下载量: 86
- 被引次数: 0
