可积谐振系统中的极端波事件研究进展

潘昌昌; Baronio Fabio; 陈世华

doi:10.7498/aps.69.20191240

摘要

从微观角度上讲, 单个极端异常波事件可视为可积模型方程的时空局域有理函数解. 本文主要讨论了三类典型的可积谐振相互作用模型(即长波短波谐振方程, 三波谐振相互作用方程, 非线性薛定谔和麦克斯韦-布洛赫方程)的基阶Peregrine异常波解及其相关研究进展; 明确指出了这些基阶异常波解形式具有普适性, 可推广应用到多分量或更高阶的可积模型中; 借助数值模拟, 还展示了共存异常波、互补异常波、以及自感应透明Peregrine孤子等新颖动力学.

关键词:

Abstract

From a microscopic perspective, the single extreme rogue wave event can be thought of as the spatiotemporally localized rational solutions of the underlying integrable model. A typical example is the fundamental Peregrine rogue wave, who in general entails a three-fold peak amplitude, while making its peak position arbitrary on a finite continuous-wave background. This kind of bizarre wave structure agrees well with the fleeting nature of realistic rogue waves and has been confirmed experimentally, first in nonlinear fibers, then in water wave tanks and plasmas, and recently in an irregular oceanic sea state. In this review, with a brief overview of the current state of the art of the concepts, methods, and research trends related to rogue wave events, we mainly discuss the fundamental Peregrine rogue wave solutions as well as their recent progress, intended for three typical integrable models, namely, the long-wave short-wave resonant equation, the three-wave resonant interaction equation, and the nonlinear Schrödinger and Maxwell–Bloch equation. Basically, while the first two models can describe the resonant interaction among optical waves, the latter governs the interaction between the optical waves and the resonant medium. For each integrable model, we present explicitly its Lax pair, Darboux transformation formulas, and fundamental Peregrine rogue wave solutions, in a self-consistent way. We confirm by convincing examples that these fundamental rogue wave solutions exhibit universality and can be applied to the multi-component or the higher-order versions of the current integrable models. By means of numerical simulations, we demonstrate as well several novel rogue wave dynamics such as coexisting rogue waves, complementary rogue waves, and Peregrine solitons of self-induced transparency.

Keywords:

作者及机构信息

1.
东南大学物理学院, 南京　211189

2.
Dipartimento di Ingegneria dell’Informazione, Università di Brescia, Via Branze 38, 25123 Brescia, Italy

通信作者: 陈世华, cshua@seu.edu.cn

基金项目: 国家自然科学基金(批准号: 11474051, 11974075)资助的课题

Authors and contacts

1.
School of Physics, Southeast University, Nanjing 211189, China

2.
Dipartimento di Ingegneria dell’Informazione, Università di Brescia, Via Branze 38, 25123 Brescia, Italy

Corresponding author: Chen Shi-Hua, cshua@seu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11474051, 11974075)

文章全文 : translate this paragraph

参考文献

[1]	Kharif C, Pelinovsky E, Slunyaev A 2009 Rogue Waves in the Ocean (Berlin: Springer)
[2]	Dysthe K, Krogstad H E, Müller P 2008 Annu. Rev. Fluid Mech. 40 287 Google Scholar
[3]	Akhmediev N, Pelinovsky E 2010 Eur. Phys. J. Spec. Top. 185 1 Google Scholar
[4]	Lawton G 2001 New Scientist 170 28
[5]	Pisarchik A N, Jaimes-Reátegui R, Sevilla-Escoboza R, Huerta-Cuellar G, Taki M 2011 Phys. Rev. Lett. 107 274101 Google Scholar
[6]	Onorato M, Resitori S, Baronio F (ed) 2016 Rogue and Shock Waves in Nonlinear Dispersive Media (Switzerland: Springer) pp179–203
[7]	Wabnitz S (ed) 2017 Nonlinear Guided Wave Optics: A Testbed for Extreme Waves (Bristol: IOP Publishing) Chapt. 11
[8]	Dudley J M, Dias F, Erkintalo M, Genty G 2014 Nat. Photonics 8 755 Google Scholar
[9]	Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi F T 2013 Phys. Rep. 528 47 Google Scholar
[10]	Moslem W M 2011 Phys. Plasmas 18 032301 Google Scholar
[11]	Alam M S, Hafez M G, Talukder M R, Ali M Hossain 2017 Chin. Phys. B 26 095203 Google Scholar
[12]	Tsai Y Y, Tsai J Y, Lin I 2016 Nat. Phys. 12 573 Google Scholar
[13]	Bludov Yu V, Konotop V V, Akhmediev N 2009 Phys. Rev. A 80 033610 Google Scholar
[14]	Wen L, Li L, Li Z D, Song S W, Zhang X F, Liu W M 2011 Eur. Phys. J. D 64 473 Google Scholar
[15]	张解放, 戴朝卿 2016 65 050501 Google Scholar Zhang J F, Dai C Q 2016 Acta Phys. Sin. 65 050501 Google Scholar
[16]	Liu C, Yang Z Y, Zhao L C, Yang W L, Yue R H 2013 Chin. Phys. Lett. 30 040304 Google Scholar
[17]	Yan Z Y 2010 Commun. Theor. Phys. 54 947 Google Scholar
[18]	Chabchoub A, Hoffmann N P, Akhmediev N 2011 Phys. Rev. Lett. 106 204502 Google Scholar
[19]	Akhmediev N, Ankiewicz A, Taki M 2009 Phys. Lett. A 373 675 Google Scholar
[20]	Solli D R, Ropers C, Koonath P, Jalali B 2007 Nature 450 1054 Google Scholar
[21]	Lecaplain C, Grelu Ph, Soto-Crespo J M, Akhmediev N 2012 Phys. Rev. Lett. 108 233901 Google Scholar
[22]	Baronio F, Degasperis A, Conforti M, Wabnitz S 2012 Phys. Rev. Lett. 109 044102 Google Scholar
[23]	Chen S, Baronio F, Soto-Crespo J M, Grelu Ph, Mihalache D 2017 J. Phys. A: Math. Theor. 50 463001 Google Scholar
[24]	Qiu D, He J, Zhang Y, Porsezian K 2015 Proc. R. Soc. A 471 20150236 Google Scholar
[25]	Peregrine D H 1983 J. Aust. Math. Soc. Ser. B: Appl. Math. 25 16 Google Scholar
[26]	Shrira V I, Geogjaev V V 2010 J. Eng. Math. 67 11 Google Scholar
[27]	Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, Akhmediev N, Dudley J M 2010 Nat. Phys. 6 790 Google Scholar
[28]	Bailung H, Sharma S K, Nakamura Y 2011 Phys. Rev. Lett. 107 255005 Google Scholar
[29]	Chabchoub A 2016 Phys. Rev. Lett. 117 144103 Google Scholar
[30]	Walczak P, Randoux S, Suret P 2015 Phys. Rev. Lett. 114 143903 Google Scholar
[31]	Picozzi A, Garnier J, Hansson T, Suret P, Randoux S, Millot G, Christodoulides D N 2014 Phys. Rep. 542 1 Google Scholar
[32]	Soto-Crespo J M, Devine N, Akhmediev N 2016 Phys. Rev. Lett. 116 103901 Google Scholar
[33]	Baronio F 2017 Opt. Lett. 42 1756 Google Scholar
[34]	Baronio F, Chen S, Mihalache D 2017 Opt. Lett. 42 3514 Google Scholar
[35]	Ankiewicz A, Soto-Crespo J M, Chowdhury M A, Akhmediev N 2013 J. Opt. Soc. Am. B 30 87 Google Scholar
[36]	Zhang J F, Jin M Z, He J D, Lou J H, Dai C Q 2013 Chin. Phys. B 22 054208 Google Scholar
[37]	Ma Z Y, Ma S H 2012 Chin. Phys. B 21 030507 Google Scholar
[38]	Chen S, Soto-Crespo J M, Grelu Ph 2014 Opt. Express 22 27632 Google Scholar
[39]	Guo B L, Ling L M 2011 Chin. Phys. Lett. 28 110202 Google Scholar
[40]	Baronio F, Conforti M, Degasperis A, Lombardo S 2013 Phys. Rev. Lett. 111 114101 Google Scholar
[41]	Grelu Ph (ed) 2016 Nonlinear Optical Cavity Dynamics: from Microresonators to Fiber Lasers (Weinheim: Wiley-VCH) pp231–316
[42]	Grelu Ph, Akhmediev N 2012 Nat. Photonics 6 84 Google Scholar
[43]	Chen S, Dudley J M 2009 Phys. Rev. Lett. 102 233903 Google Scholar
[44]	Akhmediev N, Ankiewicz A 1997 Solitons: Nonlinear Pulses and Beams (London: Chapman and Hall)
[45]	Chen S, Liu Y, Mysyrowicz A 2010 Phys. Rev. A 81 061806 Google Scholar
[46]	Guo B, Ling L, Liu Q P 2012 Phys. Rev. E 85 026607 Google Scholar
[47]	He J S, Zhang H R, Wang L H, Porsezian K, Fokas A S 2013 Phys. Rev. E 87 052914 Google Scholar
[48]	Wang D S, Zhang D J, Yang J 2010 J. Math. Phys. 51 023510 Google Scholar
[49]	Wang D S, Wang X 2018 Nonlinear Anal. Real World Appl. 41 334 Google Scholar
[50]	Chen S, Zhou Y, Baronio F, Mihalache D 2018 Rom. Rep. Phys. 70 102
[51]	Akhmediev N, Ankiewicz A, Soto-Crespo J M 2009 Phys. Rev. E 80 026601 Google Scholar
[52]	Ankiewicz A, Soto-Crespo J M, Akhmediev N 2010 Phys. Rev. E 81 046602 Google Scholar
[53]	Chen S 2013 Phys. Rev. E 88 023202 Google Scholar
[54]	Soto-Crespo J M, Devine N, Hoffmann N P, Akhmediev N 2014 Phys. Rev. E 90 032902 Google Scholar
[55]	Chan H N, Chow K W, Kedziora D J, Grimshaw R H J, Ding E 2014 Phys. Rev. E 89 032914 Google Scholar
[56]	Zhang Y, Guo L, He J, Zhou Z 2015 Lett. Math. Phys. 105 853 Google Scholar
[57]	He J, Xu S, Porsezian K 2012 J. Phys. Soc. Jpn. 81 124007 Google Scholar
[58]	Chen S, Song L Y 2014 Phys. Lett. A 378 1228 Google Scholar
[59]	Xu S, He J, Cheng Y, Porseizan K 2015 Math. Method Appl. Sci. 38 1106 Google Scholar
[60]	He J, Wang L, Li L, Porsezian K, Erdélyi R 2014 Phys. Rev. E 89 062917 Google Scholar
[61]	Chen S, Soto-Crespo J M, Baronio F, Grelu Ph, Mihalache D 2016 Opt. Express 24 15251 Google Scholar
[62]	Zha Q 2013 Phys. Scr. 87 065401 Google Scholar
[63]	Chen S, Baronio F, Soto-Crespo J M, Liu Y, Grelu Ph 2016 Phys. Rev. E 93 062202 Google Scholar
[64]	Chen S, Zhou Y, Bu L, Baronio F, Soto-Crespo J M, Mihalache D 2019 Opt. Express 27 11370 Google Scholar
[65]	Ankiewicz A, Kedziora D J, Chowdury A, Bandelow U, Akhmediev N 2016 Phys. Rev. E 93 012206 Google Scholar
[66]	Zhang Y, Guo L, Chabchoub A, He J 2017 Rom. J. Phys. 62 102
[67]	Chen S, Mihalache D 2015 J. Phys. A: Math. Theor. 48 215202 Google Scholar
[68]	Baronio F, Conforti M, Degasperis A, Lombardo S, Onorato M, Wabnitz S 2014 Phys. Rev. Lett. 113 034101 Google Scholar
[69]	Li L, Malomed B A, Mihalache D, Liu W M 2006 Phys. Rew. E 73 066610 Google Scholar
[70]	Chen S, Song L Y 2013 Phys. Rev. E 87 032910 Google Scholar
[71]	Li Z D, Huo C Z, Li Q Y, He P B, Xu T F 2018 Chin. Phys. B 27 040505 Google Scholar
[72]	Ye Y, Zhou Y, Chen S, Baronio F, Grelu Ph 2019 Proc. R. Soc. A 475 20180806 Google Scholar
[73]	Ohta Y, Yang J 2012 Phys. Rev. E 86 036604 Google Scholar
[74]	Ohta Y, Yang J 2013 J. Phys. A: Math. Theor. 46 105202 Google Scholar
[75]	Randoux S, Suret P, El G 2016 Sci. Rep. 6 29238 Google Scholar
[76]	Matveev V B, Salle M A 1991 Darboux Transformation and Solitons (Berlin: Springer)
[77]	Hirota R 1973 J. Math. Phys. 14 805 Google Scholar
[78]	Zhang N, Xia T C, Hu B B 2017 Commun. Theor. Phys. 68 580 Google Scholar
[79]	Kang Z Z, Xia T C, Ma W X 2019 Adv. Differ. Equ. NY 2019 188 Google Scholar
[80]	Kang Z Z, Xia T C, Ma W X 2019 Proc. Rom. Acad. A 20 115
[81]	Baronio F, Wabnitz S, Kodama Y 2016 Phys. Rev. Lett. 116 173901 Google Scholar
[82]	Baronio F, Chen S, Onorato M, Trillo S, Wabnitz S, Kodama Y 2016 Opt. Lett. 41 5571 Google Scholar
[83]	Bokaeeyan M, Ankiewicz A, Akhmediev N 2019 Phys. Scr. 94 035203 Google Scholar
[84]	Mihalache D 2017 Rom. Rep. Phys. 69 403
[85]	Malomed B A, Mihalache D 2019 Rom. J. Phys. 64 106
[86]	Frisquet B, Kibler B, Morin Ph, Baronio F, Conforti M, Millot G, Wabnitz S 2016 Sci. Rep. 6 20785 Google Scholar
[87]	Baronio F, Frisquet B, Chen S. Millot G, Wabnitz S, Kibler B 2018 Phys. Rev. A 97 013852 Google Scholar
[88]	Tikan A, Billet C, El G, Tovbis A, Bertola M, Sylvestre T, Gustave F, Randoux S, Genty G, Suret P, Dudley J M 2017 Phys. Rev. Lett. 119 033901 Google Scholar
[89]	Liu W, Zhang Y, He J 2018 Rom. Rep. Phys. 70 106
[90]	Chen S, Ye Y, Soto-Crespo J M, Grelu Ph, Baronio F 2018 Phys. Rev. Lett. 121 104101 Google Scholar
[91]	Kibler B, Chabchoub A, Gelash A, Akhmediev N, Zakharov V E 2015 Phys. Rev. X 5 041026 Google Scholar
[92]	Chen S, Grelu Ph, Soto-Crespo J M 2014 Phys. Rev. E 89 011201 Google Scholar
[93]	Chen S, Baronio F, Soto-Crespo J M, Grelu Ph, Conforti M, Wabnitz S 2015 Phys. Rev. A 92 033847 Google Scholar
[94]	He J, Xu S, Porseizan K 2012 Phys. Rev. E 86 066603 Google Scholar
[95]	Chen S, Ye Y, Baronio F, Liu Y, Cai, X M, Grelu Ph 2017 Opt. Express 25 29687 Google Scholar
[96]	Wang X, Li Y, Huang F, Chen Y 2015 Commun. Nonlinear Sci. Numer. Simul. 20 434 Google Scholar
[97]	Degasperis A, Wabnitz S, Aceves A B 2015 Phys. Lett. A 379 1067 Google Scholar
[98]	Guo L, Wang L, Cheng Y, He J 2017 Commun. Nonlinear Sci. Numer. Simul. 52 11 Google Scholar
[99]	Zakharov V E 1972 Sov. Phys. JETP 35 908
[100]	Benney D J 1977 Stud. Appl. Math. 56 81 Google Scholar
[101]	Djordjevic V D, Redekopp L G 1977 J. Fluid Mech. 79 703 Google Scholar
[102]	Chowdhury A, Tataronis J A 2008 Phys. Rev. Lett. 100 153905 Google Scholar
[103]	Shats M, Punzmann H, Xia H 2010 Phys. Rev. Lett. 104 104503 Google Scholar
[104]	Chow K W, Chan H N, Kedziora D J, Grimshaw R H J 2013 J. Phys. Soc. Jpn. 82 074001 Google Scholar
[105]	Chan H N, Grimshaw R H J, Chow K W 2018 Phys. Rev. Fluids 3 124801 Google Scholar
[106]	Wright III O C 2006 Stud. Appl. Math. 117 71
[107]	Chen S 2014 Phys. Lett. A 378 1095 Google Scholar
[108]	Baronio F, Chen S, Grelu Ph, Wabnitz S, Conforti M 2015 Phys. Rev. A 91 033804 Google Scholar
[109]	Chen S, Soto-Crespo J M, Grelu Ph 2014 Phys. Rev. E 90 033203 Google Scholar
[110]	Kaup D J, Reiman A, Bers A 1979 Rev. Mod. Phys. 51 275 Google Scholar
[111]	Ibragimov E, Struthers A 1996 Opt. Lett. 21 1582 Google Scholar
[112]	Conforti M, Baronio F, Degasperis A, Wabnitz S 2007 Opt. Express 15 12246 Google Scholar
[113]	Abdolvand A, Nazarkin A, Chugreev A V, Kaminski C F, Russell P St J 2009 Phys. Rev. Lett. 103 183902 Google Scholar
[114]	Picholle E, Montes C, Leycuras C, Legrand O, Botineau J 1991 Phys. Rev. Lett. 66 1454 Google Scholar
[115]	Taranenko Y N, Kazovsky L G 1992 IEEE Photonics Technol. Lett. 4 494 Google Scholar
[116]	Baronio F, Conforti M, Degasperis A, Wabnitz S 2008 IEEE J. Quantum Electron. 44 542 Google Scholar
[117]	Picozzi A, Haelterman M 2001 Phys. Rev. Lett. 86 2010 Google Scholar
[118]	Malkin V M, Shvets G, Fisch N J 1999 Phys. Rev. Lett. 82 4448 Google Scholar
[119]	Buryak A V, Di Trapani P, Skryabin D V, Trillo S 2002 Phys. Rep. 370 63 Google Scholar
[120]	Baronio F, Conforti M, De Angelis C, Degasperis A, Andreana M, Couderc V, Barthélémy A 2010 Phys. Rev. Lett. 104 113902 Google Scholar
[121]	Degasperis A, Lombardo S 2006 Physica D 214 157 Google Scholar
[122]	Chen S, Cai X M, Grelu Ph, Soto-Crespo J M, Wabnitz S, Baronio F 2016 Opt. Express 24 5886 Google Scholar
[123]	Russell P St J, Culverhouse D, Farahi F 1991 IEEE J. Quantum Electron. 27 836 Google Scholar
[124]	Allen L, Eberly J H 1975 Optical Resonance and Two-Level Atoms (New York: Wiley)
[125]	Haus H A 1979 Rev. Mod. Phys. 51 331 Google Scholar
[126]	McCall S L, Hahn E L 1967 Phys. Rev. Lett. 18 908 Google Scholar
[127]	Nakazawa M, Yamada E, Kubota H 1991 Phys. Rev. A 44 5973 Google Scholar
[128]	He J S, Cheng Y, Li Y S 2002 Commun. Theor. Phys. 38 493 Google Scholar
[129]	Li C, He J, Porsezian K 2013 Phys. Rev. E 87 012913 Google Scholar
[130]	Conforti M, Baronio F 2011 Eur. Phys. J. D 64 115 Google Scholar
[131]	Wu C F, Grimshaw R H J, Chow K W, Chan H N 2015 Chaos 25 103113 Google Scholar
[132]	Tsuchida T 2002 J. Phys. A: Math. Gen. 35 7827 Google Scholar

施引文献

图 1 数值模拟验证初始白噪声微扰下的基阶RW解(5)式, (6)式和 (10)式的稳定性, 左列图对应$(m, n) =(-1.3514, ~0.7803)$, 中列图对应$(m, n) =(- 0.4287, ~0.6442)$. 右列图显示这两类RW结构在同一背景场中的数值激发. 图改编自文献[109]

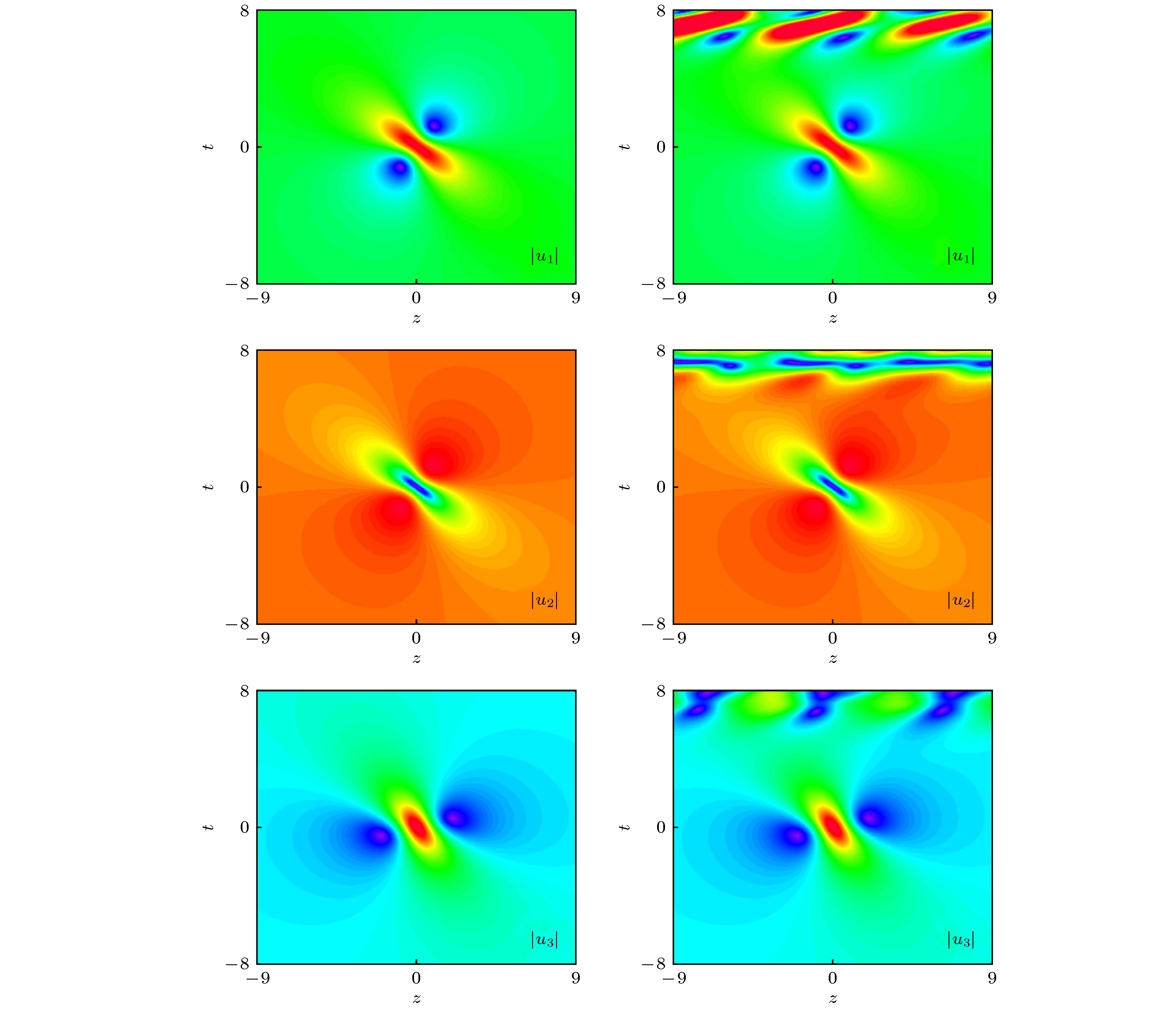
Fig. 1. Simulations confirm the stability of the fundamental RW solutions (5), (6), and (10) against initial white noise perturbations. Left column: $(m, n) =(-1.3514, ~0.7803)$; Middle column: $(m, n) =(- 0.4287, ~0.6442)$. The right column shows the numerical excitation of such two rogue wave families from the same background field. Figure adapted from Ref. [109].

下载: 全尺寸图片幻灯片

图 2 互补型基阶RW解(18)式的数值模拟结果. 左列图: 未微扰情形; 右列图: 白噪声微扰情形. 图摘自文献[122]

Fig. 2. Simulation results of the complementary fundamental rogue wave solutions (18). Left column: unperturbed; Right column: perturbed by initial white noises. Figure adapted from Ref. [122].

下载: 全尺寸图片幻灯片

图 3 NLS–MB方程的基阶RW解(23)的时空演化, 其中(a)列图对应解析解的3D曲面和轮廓图; (b)列图为数值模拟结果, 初始条件已文中给出; (c)列图显示这类异常波结构在背景场中的数值激发产生, 已黑线圈出. 图改编自文献[95]

Fig. 3. Spatiotemporal evolution of the fundamental rogue wave solutions (23) of the NLS–MB equation. Column (a): Analytical solutions, given by 3D surface and contour plots; Column (b) the numerical results, with initial conditions being specified in the text; The column (c) shows the numerical excitation of the rogue waves, indicated by the black circles, from the background field. Figure adapted from Ref. [95].

下载: 全尺寸图片幻灯片

map

[1]	Kharif C, Pelinovsky E, Slunyaev A 2009 Rogue Waves in the Ocean (Berlin: Springer)
[2]	Dysthe K, Krogstad H E, Müller P 2008 Annu. Rev. Fluid Mech. 40 287 Google Scholar
[3]	Akhmediev N, Pelinovsky E 2010 Eur. Phys. J. Spec. Top. 185 1 Google Scholar
[4]	Lawton G 2001 New Scientist 170 28
[5]	Pisarchik A N, Jaimes-Reátegui R, Sevilla-Escoboza R, Huerta-Cuellar G, Taki M 2011 Phys. Rev. Lett. 107 274101 Google Scholar
[6]	Onorato M, Resitori S, Baronio F (ed) 2016 Rogue and Shock Waves in Nonlinear Dispersive Media (Switzerland: Springer) pp179–203
[7]	Wabnitz S (ed) 2017 Nonlinear Guided Wave Optics: A Testbed for Extreme Waves (Bristol: IOP Publishing) Chapt. 11
[8]	Dudley J M, Dias F, Erkintalo M, Genty G 2014 Nat. Photonics 8 755 Google Scholar
[9]	Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi F T 2013 Phys. Rep. 528 47 Google Scholar
[10]	Moslem W M 2011 Phys. Plasmas 18 032301 Google Scholar
[11]	Alam M S, Hafez M G, Talukder M R, Ali M Hossain 2017 Chin. Phys. B 26 095203 Google Scholar
[12]	Tsai Y Y, Tsai J Y, Lin I 2016 Nat. Phys. 12 573 Google Scholar
[13]	Bludov Yu V, Konotop V V, Akhmediev N 2009 Phys. Rev. A 80 033610 Google Scholar
[14]	Wen L, Li L, Li Z D, Song S W, Zhang X F, Liu W M 2011 Eur. Phys. J. D 64 473 Google Scholar
[15]	张解放, 戴朝卿 2016 65 050501 Google Scholar Zhang J F, Dai C Q 2016 Acta Phys. Sin. 65 050501 Google Scholar
[16]	Liu C, Yang Z Y, Zhao L C, Yang W L, Yue R H 2013 Chin. Phys. Lett. 30 040304 Google Scholar
[17]	Yan Z Y 2010 Commun. Theor. Phys. 54 947 Google Scholar
[18]	Chabchoub A, Hoffmann N P, Akhmediev N 2011 Phys. Rev. Lett. 106 204502 Google Scholar
[19]	Akhmediev N, Ankiewicz A, Taki M 2009 Phys. Lett. A 373 675 Google Scholar
[20]	Solli D R, Ropers C, Koonath P, Jalali B 2007 Nature 450 1054 Google Scholar
[21]	Lecaplain C, Grelu Ph, Soto-Crespo J M, Akhmediev N 2012 Phys. Rev. Lett. 108 233901 Google Scholar
[22]	Baronio F, Degasperis A, Conforti M, Wabnitz S 2012 Phys. Rev. Lett. 109 044102 Google Scholar
[23]	Chen S, Baronio F, Soto-Crespo J M, Grelu Ph, Mihalache D 2017 J. Phys. A: Math. Theor. 50 463001 Google Scholar
[24]	Qiu D, He J, Zhang Y, Porsezian K 2015 Proc. R. Soc. A 471 20150236 Google Scholar
[25]	Peregrine D H 1983 J. Aust. Math. Soc. Ser. B: Appl. Math. 25 16 Google Scholar
[26]	Shrira V I, Geogjaev V V 2010 J. Eng. Math. 67 11 Google Scholar
[27]	Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, Akhmediev N, Dudley J M 2010 Nat. Phys. 6 790 Google Scholar
[28]	Bailung H, Sharma S K, Nakamura Y 2011 Phys. Rev. Lett. 107 255005 Google Scholar
[29]	Chabchoub A 2016 Phys. Rev. Lett. 117 144103 Google Scholar
[30]	Walczak P, Randoux S, Suret P 2015 Phys. Rev. Lett. 114 143903 Google Scholar
[31]	Picozzi A, Garnier J, Hansson T, Suret P, Randoux S, Millot G, Christodoulides D N 2014 Phys. Rep. 542 1 Google Scholar
[32]	Soto-Crespo J M, Devine N, Akhmediev N 2016 Phys. Rev. Lett. 116 103901 Google Scholar
[33]	Baronio F 2017 Opt. Lett. 42 1756 Google Scholar
[34]	Baronio F, Chen S, Mihalache D 2017 Opt. Lett. 42 3514 Google Scholar
[35]	Ankiewicz A, Soto-Crespo J M, Chowdhury M A, Akhmediev N 2013 J. Opt. Soc. Am. B 30 87 Google Scholar
[36]	Zhang J F, Jin M Z, He J D, Lou J H, Dai C Q 2013 Chin. Phys. B 22 054208 Google Scholar
[37]	Ma Z Y, Ma S H 2012 Chin. Phys. B 21 030507 Google Scholar
[38]	Chen S, Soto-Crespo J M, Grelu Ph 2014 Opt. Express 22 27632 Google Scholar
[39]	Guo B L, Ling L M 2011 Chin. Phys. Lett. 28 110202 Google Scholar
[40]	Baronio F, Conforti M, Degasperis A, Lombardo S 2013 Phys. Rev. Lett. 111 114101 Google Scholar
[41]	Grelu Ph (ed) 2016 Nonlinear Optical Cavity Dynamics: from Microresonators to Fiber Lasers (Weinheim: Wiley-VCH) pp231–316
[42]	Grelu Ph, Akhmediev N 2012 Nat. Photonics 6 84 Google Scholar
[43]	Chen S, Dudley J M 2009 Phys. Rev. Lett. 102 233903 Google Scholar
[44]	Akhmediev N, Ankiewicz A 1997 Solitons: Nonlinear Pulses and Beams (London: Chapman and Hall)
[45]	Chen S, Liu Y, Mysyrowicz A 2010 Phys. Rev. A 81 061806 Google Scholar
[46]	Guo B, Ling L, Liu Q P 2012 Phys. Rev. E 85 026607 Google Scholar
[47]	He J S, Zhang H R, Wang L H, Porsezian K, Fokas A S 2013 Phys. Rev. E 87 052914 Google Scholar
[48]	Wang D S, Zhang D J, Yang J 2010 J. Math. Phys. 51 023510 Google Scholar
[49]	Wang D S, Wang X 2018 Nonlinear Anal. Real World Appl. 41 334 Google Scholar
[50]	Chen S, Zhou Y, Baronio F, Mihalache D 2018 Rom. Rep. Phys. 70 102
[51]	Akhmediev N, Ankiewicz A, Soto-Crespo J M 2009 Phys. Rev. E 80 026601 Google Scholar
[52]	Ankiewicz A, Soto-Crespo J M, Akhmediev N 2010 Phys. Rev. E 81 046602 Google Scholar
[53]	Chen S 2013 Phys. Rev. E 88 023202 Google Scholar
[54]	Soto-Crespo J M, Devine N, Hoffmann N P, Akhmediev N 2014 Phys. Rev. E 90 032902 Google Scholar
[55]	Chan H N, Chow K W, Kedziora D J, Grimshaw R H J, Ding E 2014 Phys. Rev. E 89 032914 Google Scholar
[56]	Zhang Y, Guo L, He J, Zhou Z 2015 Lett. Math. Phys. 105 853 Google Scholar
[57]	He J, Xu S, Porsezian K 2012 J. Phys. Soc. Jpn. 81 124007 Google Scholar
[58]	Chen S, Song L Y 2014 Phys. Lett. A 378 1228 Google Scholar
[59]	Xu S, He J, Cheng Y, Porseizan K 2015 Math. Method Appl. Sci. 38 1106 Google Scholar
[60]	He J, Wang L, Li L, Porsezian K, Erdélyi R 2014 Phys. Rev. E 89 062917 Google Scholar
[61]	Chen S, Soto-Crespo J M, Baronio F, Grelu Ph, Mihalache D 2016 Opt. Express 24 15251 Google Scholar
[62]	Zha Q 2013 Phys. Scr. 87 065401 Google Scholar
[63]	Chen S, Baronio F, Soto-Crespo J M, Liu Y, Grelu Ph 2016 Phys. Rev. E 93 062202 Google Scholar
[64]	Chen S, Zhou Y, Bu L, Baronio F, Soto-Crespo J M, Mihalache D 2019 Opt. Express 27 11370 Google Scholar
[65]	Ankiewicz A, Kedziora D J, Chowdury A, Bandelow U, Akhmediev N 2016 Phys. Rev. E 93 012206 Google Scholar
[66]	Zhang Y, Guo L, Chabchoub A, He J 2017 Rom. J. Phys. 62 102
[67]	Chen S, Mihalache D 2015 J. Phys. A: Math. Theor. 48 215202 Google Scholar
[68]	Baronio F, Conforti M, Degasperis A, Lombardo S, Onorato M, Wabnitz S 2014 Phys. Rev. Lett. 113 034101 Google Scholar
[69]	Li L, Malomed B A, Mihalache D, Liu W M 2006 Phys. Rew. E 73 066610 Google Scholar
[70]	Chen S, Song L Y 2013 Phys. Rev. E 87 032910 Google Scholar
[71]	Li Z D, Huo C Z, Li Q Y, He P B, Xu T F 2018 Chin. Phys. B 27 040505 Google Scholar
[72]	Ye Y, Zhou Y, Chen S, Baronio F, Grelu Ph 2019 Proc. R. Soc. A 475 20180806 Google Scholar
[73]	Ohta Y, Yang J 2012 Phys. Rev. E 86 036604 Google Scholar
[74]	Ohta Y, Yang J 2013 J. Phys. A: Math. Theor. 46 105202 Google Scholar
[75]	Randoux S, Suret P, El G 2016 Sci. Rep. 6 29238 Google Scholar
[76]	Matveev V B, Salle M A 1991 Darboux Transformation and Solitons (Berlin: Springer)
[77]	Hirota R 1973 J. Math. Phys. 14 805 Google Scholar
[78]	Zhang N, Xia T C, Hu B B 2017 Commun. Theor. Phys. 68 580 Google Scholar
[79]	Kang Z Z, Xia T C, Ma W X 2019 Adv. Differ. Equ. NY 2019 188 Google Scholar
[80]	Kang Z Z, Xia T C, Ma W X 2019 Proc. Rom. Acad. A 20 115
[81]	Baronio F, Wabnitz S, Kodama Y 2016 Phys. Rev. Lett. 116 173901 Google Scholar
[82]	Baronio F, Chen S, Onorato M, Trillo S, Wabnitz S, Kodama Y 2016 Opt. Lett. 41 5571 Google Scholar
[83]	Bokaeeyan M, Ankiewicz A, Akhmediev N 2019 Phys. Scr. 94 035203 Google Scholar
[84]	Mihalache D 2017 Rom. Rep. Phys. 69 403
[85]	Malomed B A, Mihalache D 2019 Rom. J. Phys. 64 106
[86]	Frisquet B, Kibler B, Morin Ph, Baronio F, Conforti M, Millot G, Wabnitz S 2016 Sci. Rep. 6 20785 Google Scholar
[87]	Baronio F, Frisquet B, Chen S. Millot G, Wabnitz S, Kibler B 2018 Phys. Rev. A 97 013852 Google Scholar
[88]	Tikan A, Billet C, El G, Tovbis A, Bertola M, Sylvestre T, Gustave F, Randoux S, Genty G, Suret P, Dudley J M 2017 Phys. Rev. Lett. 119 033901 Google Scholar
[89]	Liu W, Zhang Y, He J 2018 Rom. Rep. Phys. 70 106
[90]	Chen S, Ye Y, Soto-Crespo J M, Grelu Ph, Baronio F 2018 Phys. Rev. Lett. 121 104101 Google Scholar
[91]	Kibler B, Chabchoub A, Gelash A, Akhmediev N, Zakharov V E 2015 Phys. Rev. X 5 041026 Google Scholar
[92]	Chen S, Grelu Ph, Soto-Crespo J M 2014 Phys. Rev. E 89 011201 Google Scholar
[93]	Chen S, Baronio F, Soto-Crespo J M, Grelu Ph, Conforti M, Wabnitz S 2015 Phys. Rev. A 92 033847 Google Scholar
[94]	He J, Xu S, Porseizan K 2012 Phys. Rev. E 86 066603 Google Scholar
[95]	Chen S, Ye Y, Baronio F, Liu Y, Cai, X M, Grelu Ph 2017 Opt. Express 25 29687 Google Scholar
[96]	Wang X, Li Y, Huang F, Chen Y 2015 Commun. Nonlinear Sci. Numer. Simul. 20 434 Google Scholar
[97]	Degasperis A, Wabnitz S, Aceves A B 2015 Phys. Lett. A 379 1067 Google Scholar
[98]	Guo L, Wang L, Cheng Y, He J 2017 Commun. Nonlinear Sci. Numer. Simul. 52 11 Google Scholar
[99]	Zakharov V E 1972 Sov. Phys. JETP 35 908
[100]	Benney D J 1977 Stud. Appl. Math. 56 81 Google Scholar
[101]	Djordjevic V D, Redekopp L G 1977 J. Fluid Mech. 79 703 Google Scholar
[102]	Chowdhury A, Tataronis J A 2008 Phys. Rev. Lett. 100 153905 Google Scholar
[103]	Shats M, Punzmann H, Xia H 2010 Phys. Rev. Lett. 104 104503 Google Scholar
[104]	Chow K W, Chan H N, Kedziora D J, Grimshaw R H J 2013 J. Phys. Soc. Jpn. 82 074001 Google Scholar
[105]	Chan H N, Grimshaw R H J, Chow K W 2018 Phys. Rev. Fluids 3 124801 Google Scholar
[106]	Wright III O C 2006 Stud. Appl. Math. 117 71
[107]	Chen S 2014 Phys. Lett. A 378 1095 Google Scholar
[108]	Baronio F, Chen S, Grelu Ph, Wabnitz S, Conforti M 2015 Phys. Rev. A 91 033804 Google Scholar
[109]	Chen S, Soto-Crespo J M, Grelu Ph 2014 Phys. Rev. E 90 033203 Google Scholar
[110]	Kaup D J, Reiman A, Bers A 1979 Rev. Mod. Phys. 51 275 Google Scholar
[111]	Ibragimov E, Struthers A 1996 Opt. Lett. 21 1582 Google Scholar
[112]	Conforti M, Baronio F, Degasperis A, Wabnitz S 2007 Opt. Express 15 12246 Google Scholar
[113]	Abdolvand A, Nazarkin A, Chugreev A V, Kaminski C F, Russell P St J 2009 Phys. Rev. Lett. 103 183902 Google Scholar
[114]	Picholle E, Montes C, Leycuras C, Legrand O, Botineau J 1991 Phys. Rev. Lett. 66 1454 Google Scholar
[115]	Taranenko Y N, Kazovsky L G 1992 IEEE Photonics Technol. Lett. 4 494 Google Scholar
[116]	Baronio F, Conforti M, Degasperis A, Wabnitz S 2008 IEEE J. Quantum Electron. 44 542 Google Scholar
[117]	Picozzi A, Haelterman M 2001 Phys. Rev. Lett. 86 2010 Google Scholar
[118]	Malkin V M, Shvets G, Fisch N J 1999 Phys. Rev. Lett. 82 4448 Google Scholar
[119]	Buryak A V, Di Trapani P, Skryabin D V, Trillo S 2002 Phys. Rep. 370 63 Google Scholar
[120]	Baronio F, Conforti M, De Angelis C, Degasperis A, Andreana M, Couderc V, Barthélémy A 2010 Phys. Rev. Lett. 104 113902 Google Scholar
[121]	Degasperis A, Lombardo S 2006 Physica D 214 157 Google Scholar
[122]	Chen S, Cai X M, Grelu Ph, Soto-Crespo J M, Wabnitz S, Baronio F 2016 Opt. Express 24 5886 Google Scholar
[123]	Russell P St J, Culverhouse D, Farahi F 1991 IEEE J. Quantum Electron. 27 836 Google Scholar
[124]	Allen L, Eberly J H 1975 Optical Resonance and Two-Level Atoms (New York: Wiley)
[125]	Haus H A 1979 Rev. Mod. Phys. 51 331 Google Scholar
[126]	McCall S L, Hahn E L 1967 Phys. Rev. Lett. 18 908 Google Scholar
[127]	Nakazawa M, Yamada E, Kubota H 1991 Phys. Rev. A 44 5973 Google Scholar
[128]	He J S, Cheng Y, Li Y S 2002 Commun. Theor. Phys. 38 493 Google Scholar
[129]	Li C, He J, Porsezian K 2013 Phys. Rev. E 87 012913 Google Scholar
[130]	Conforti M, Baronio F 2011 Eur. Phys. J. D 64 115 Google Scholar
[131]	Wu C F, Grimshaw R H J, Chow K W, Chan H N 2015 Chaos 25 103113 Google Scholar
[132]	Tsuchida T 2002 J. Phys. A: Math. Gen. 35 7827 Google Scholar

[1]	安新磊, 乔帅, 张莉. 基于麦克斯韦电磁场理论的神经元动力学响应与隐藏放电控制. , 2021, 70(5): 050501. doi: 10.7498/aps.70.20201347
[2]	赖煜成, 陈苏琪, 牟兰雅, 王兆娜. 基于麦克斯韦方程组的纳米尺度电磁边界条件. , 2021, 70(23): 230301. doi: 10.7498/aps.70.20211025
[3]	李树. 光子与相对论麦克斯韦分布电子散射的能谱角度谱研究. , 2019, 68(1): 015201. doi: 10.7498/aps.68.20181796
[4]	朱燕清, 张丹伟, 朱诗亮. 用光晶格模拟狄拉克、外尔和麦克斯韦方程. , 2019, 68(4): 046701. doi: 10.7498/aps.68.20181929
[5]	李树. 光子与相对论麦克斯韦分布电子散射截面的蒙特卡罗计算方法. , 2018, 67(21): 215201. doi: 10.7498/aps.67.20180932
[6]	胡亮, 罗懋康. 柱面非线性麦克斯韦方程组的行波解. , 2017, 66(13): 130302. doi: 10.7498/aps.66.130302
[7]	林福忠, 马松华. (2+1)维色散长波方程的新精确解及其复合波激发. , 2014, 63(4): 040508. doi: 10.7498/aps.63.040508
[8]	李学良, 石雁祥. 双麦克斯韦分布尘埃等离子体中尘埃粒子的充电研究. , 2014, 63(21): 215201. doi: 10.7498/aps.63.215201
[9]	文文, 李慧军, 陈秉岩. 强相互作用费米气体在谐振子势中的干涉演化. , 2012, 61(22): 220306. doi: 10.7498/aps.61.220306
[10]	王亚伟, 刘明礼, 刘仁杰, 雷海娜, 田相龙. Fabry-Perot腔谐振对横电波激励下亚波长一维金属光栅的异常透射性的作用. , 2011, 60(2): 024217. doi: 10.7498/aps.60.024217
[11]	满达夫, 那仁满都拉. 具有能量输入/输出的固体层中孤立波的传播及相互作用特性. , 2010, 59(1): 60-66. doi: 10.7498/aps.59.60
[12]	王媛媛, 张彩虹, 马金龙, 金飙兵, 许伟伟, 康琳, 陈健, 吴培亨. 亚波长孔阵列的太赫兹波异常透射研究. , 2009, 58(10): 6884-6888. doi: 10.7498/aps.58.6884
[13]	贾飞, 谢双媛, 羊亚平. 非旋波近似下频率变化的场与原子的相互作用. , 2006, 55(11): 5835-5841. doi: 10.7498/aps.55.5835
[14]	巩华荣, 宫玉彬, 魏彦玉, 唐昌建, 薛东海, 王文祥. 考虑到束-波相互作用的速调管离子噪声二维模拟. , 2006, 55(10): 5368-5374. doi: 10.7498/aps.55.5368
[15]	套格图桑, 斯仁道尔吉. 非线性长波方程组和Benjamin方程的新精确孤波解. , 2006, 55(7): 3246-3254. doi: 10.7498/aps.55.3246
[16]	郭冠平, 张解放. 长短波相互作用方程的Jacobi椭圆函数求解. , 2003, 52(11): 2660-2663. doi: 10.7498/aps.52.2660
[17]	刘三秋, 郭琴, 陶向阳, 付传鸿. 非旋波近似下级联型三能级原子与腔场相互作用的量子动力学性质. , 1998, 47(9): 1481-1488. doi: 10.7498/aps.47.1481
[18]	余玮, 徐至展, 马锦秀, 陈荣清. 等离子体拍频波加速器中三波相互作用的时间发展. , 1993, 42(3): 431-436. doi: 10.7498/aps.42.431
[19]	贺凯芬. 耗散三波相互作用定态的Hopf分岔. , 1987, 36(11): 1451-1458. doi: 10.7498/aps.36.1451
[20]	秦运文. 关于辐射在双麦克斯韦等离子体中散射的结构因子. , 1984, 33(4): 561-563. doi: 10.7498/aps.33.561

计量

文章访问数: 9585
PDF下载量: 197
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

可积谐振系统中的极端波事件研究进展