-
基于密度泛函理论和投影缀加波赝势方法, 采用广义梯度近似算法研究了碱金属(Li, Na, K和Rb)和碱土金属(Be, Mg和Sr)掺杂二维GaN单层的电子结构和磁学性质. 研究表明, 除Be原子位于GaN单层平面内之外, 其余掺杂原子均略微隆起于平面. 通过比较七种掺杂体系在不同环境下的形成能, 发现在富N环境中更易实现掺杂. 能带结构表明: 四种碱金属原子掺杂体系是磁性半导体, 总磁矩为2μB; 三种碱土金属掺杂体系呈半金属性, 总磁矩为1μB. 磁耦合计算表明, 七种元素掺杂体系均存在长程铁磁耦合. 采用海森伯平均场模型估算双掺杂体系的居里温度, 发现Li, Be, Mg和Sr的长程铁磁耦合态居里温度均高于室温, 表明这4种原子掺杂的二维GaN单层是很好的室温铁磁性备选材料.We systematically study the electronic structure and magnetic properties of alkali metals (Li, Na, K and Rb) and alkaline earth metals (Be, Mg and Sr) doped two-dimensional GaN monolayers using the first-principles calculations based on density functional theory. The results show that Be atom is located in the plane of the GaN monolayer, and the other doped atoms reside slightly above the plane. It is found that doping is easier to achieve under the N-rich condition. The total magnetic moment of the alkali metals doped system and the alkaline earth metals doped system are 2μB and 1μB, respectively, which are presented mainly by the spin-polarized holes of the nearest N atoms of the impurity atoms. The band structures indicate that the four alkali metal atoms doped systems are magnetic semiconductors, and the three alkaline earth metal doped systems are all semi-metallic. For a double M-doped GaN monolayer system, there is a long-range ferromagnetic coupling in the seven elements doped systems, which are realized by the hole-mediated p-p hybrid interaction. The Heisenberg mean field model is used to estimate the Curie temperature. It is found that the long-range ferromagnetic coupling states of Li, Be, Mg and Sr are existent at higher than room temperature, indicating that the four atom-doped two-dimensional GaN monolayers are very good candidates for the room temperature ferromagnetic candidate materials. The alkali metals and alkaline earth metals doped two-dimensional GaN monolayers are expected to play an important role in the studying of spintronics.
-
Keywords:
- two-dimensional GaN monolayer /
- electronic structure /
- room temperature ferromagnetism /
- first-principles
[1] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[2] Srivastava P, Hembram K, Mizuseki H, Lee K R, Han S S, Kim S 2015 J. Phys. Chem. C 119 6530
Google Scholar
[3] Wang Q H, Kalantar-Zadeh K, Kis A, Coleman J N, Strano M S 2012 Nat. Nanotechnol. 7 699
Google Scholar
[4] Prinz G A 1998 Science 282 1660
Google Scholar
[5] Wolf S A, Awschalom D D, Buhrman R A, Daughton J M, von Molnar S, Roukes M L, Chtchelkanova A Y, Treger D M 2001 Science 294 1488
Google Scholar
[6] Feng B J, Ding Z J, Meng S, Yao Y G, He X Y, Cheng P, Chen L, Wu K H 2012 Nano Lett. 12 3507
Google Scholar
[7] Liu H, Neal A T, Zhu Z, Luo Z, Xu X F, Tománek D, Ye P D 2014 ACS Nano 8 4033
Google Scholar
[8] Li L K, Yu Y J, Ye G J, Ge Q Q, Ou X D, Wu H, Feng D L, Chen X H, Zhang Y B 2014 Nat. Nanotechnol. 9 372
Google Scholar
[9] Wei J W, Ma Z W, Zeng H, Wang Z Y, Wei Q, Peng P 2012 Aip Adv. 2 042141
Google Scholar
[10] Tongay S, Zhou J, Ataca C, Lo K, Matthews T S, Li J B, Grossman J C, Wu J Q 2012 Nano Lett. 12 5576
Google Scholar
[11] Song L, Ci L J, Lu H, Sorokin P B, Jin C H, Ni J, Kvashnin A G, Kvashnin D G, Lou J, Yakobson B I, Ajayan P M 2010 Nano Lett. 10 3209
Google Scholar
[12] 徐大庆, 赵子涵, 李培咸, 王超, 张岩, 刘树林, 童军 2018 67 087501
Google Scholar
Xu D Q, Zhao Z H, Li P X, Wang C, Zhang Y, Liu S L, Tong J 2018 Acta Phys. Sin. 67 087501
Google Scholar
[13] Chen G X, Wang D D, Zhang J M, Xu K W 2013 Phys. Status Solidi B 250 1510
Google Scholar
[14] Nakamura S, Mukai T, Senoh M 1994 Appl. Phys. Lett. 64 1687
Google Scholar
[15] Nakamura S 1998 Science 281 956
Google Scholar
[16] Al Balushi Z Y, Wang K, Ghosh R K, Vilá R A, Eichfeld S M, Caldwell J D, Qin X, Lin Y C, Desario P A, Stone G, Subramanian S, Paul D F, Wallace R M, Datta S, Redwing J M, Robinson J A 2016 Nat. Mater. 15 1166
Google Scholar
[17] Dietl T, Ohno H, Matsukura F, Cibert J, Ferrand D 2000 Science 287 1019
Google Scholar
[18] Overberg M E, Abernathy C R, Pearton S J, Theodoropoulou N A, McCarthy K T, Hebard A F 2001 Appl. Phys. Lett. 79 1312
Google Scholar
[19] Sasaki T, Sonoda S, Yamamoto Y, Suga K I, Shimizu S, Kindo K, Hori H 2002 J. Appl. Phys. 91 7911
Google Scholar
[20] Liu H X, Wu S Y, Singh R K, Lin G, Smith D J, Newman N, Dilley N R, Montes L, Simmonds M B 2004 Appl. Phys. Lett. 85 4076
Google Scholar
[21] Wu R Q, Peng G W, Liu L, Feng Y P, Huang Z G, Wu Q Y 2006 Appl. Phys. Lett. 89 062505
Google Scholar
[22] Fukumura T, Jin Z, Kawasaki M, Shono T, Hasegawa T, Koshihara S, Koinuma H 2001 Appl. Phys. Lett. 78 958
Google Scholar
[23] Xiao G, Wang L L, Rong Q Y, Xu H Q, Xiao W Z 2016 Comput. Mater. Sci. 124 98
Google Scholar
[24] Venkatesan M, Fitzgerald C B, Coey J M D 2004 Nature 430 630
Google Scholar
[25] Coey J M D 2005 Solid State Sci. 7 660
Google Scholar
[26] Ren J, Zhang S B, Liu P P 2019 Chin. Phys. Lett. 36 076101
Google Scholar
[27] Pan H, Yi J B, Shen L, Wu R Q, Yang J H, Lin J Y, Feng Y P, Ding J, Van L H, Yin J H 2007 Phys. Rev. Lett. 99 127201
Google Scholar
[28] Xiao G, Wang L L, Rong Q Y, Xu H Q, Xiao W Z 2016 Phys. Status Solidi B 253 1816
Google Scholar
[29] Han R L, Chen X Y, Yan Y 2017 Chin. Phys. B 26 097503
Google Scholar
[30] 潘凤春, 徐佳楠, 杨花, 林雪玲, 陈焕铭 2017 66 056101
Google Scholar
Pan F C, Xu J N, Yang H, Lin X L, Chen H M 2017 Acta Phys. Sin. 66 056101
Google Scholar
[31] 张梅玲, 陈玉红, 张材荣, 李公平 2019 68 087101
Google Scholar
Zhang M L, Chen Y H, Zhang C R, Li G P 2019 Acta Phys. Sin. 68 087101
Google Scholar
[32] Sundaresan A, Bhargavi R, Rangarajan N 2006 Phys. Rev. B 74 161306
Google Scholar
[33] Dev P, Xue Y, Zhang P 2008 Phys. Rev. Lett. 100 117204
Google Scholar
[34] Yang K S, Wu R Q, Shen L, Feng Y P, Dai Y, Huang B B 2010 Phys. Rev. B 81 125211
Google Scholar
[35] 侯清玉, 李勇, 赵春旺 2017 66 067202
Google Scholar
Hou Q Y, Li Y, Zhao C W 2017 Acta Phys. Sin. 66 067202
Google Scholar
[36] 黄毅华, 江东亮, 张辉, 陈忠明, 黄政仁 2017 66 017501
Google Scholar
Huang Y H, Jiang D L, Zhang H, Chen Z M, Huang Z R 2017 Acta Phys. Sin. 66 017501
Google Scholar
[37] Kresse G, Hafner J 1994 Phys. Rev. B 49 14251
Google Scholar
[38] Kresse G, Furthmüller J 1996 Comput. Mater. Sci. 6 15
Google Scholar
[39] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169
Google Scholar
[40] Blöchl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[41] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
Google Scholar
[42] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[43] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188
Google Scholar
[44] Şahin H, Cahangirov S, Topsakal M, Bekaroglu E, Akturk E, Senger R T, Ciraci S 2009 Phys. Rev. B 80 155453
Google Scholar
[45] Lee S M, Lee Y H, Hwang Y G, Elsner J, Porezag D, Frauenheim T 1999 Phys. Rev. B 60 7788
Google Scholar
[46] Maruska H P, Tietjen J J 1969 Appl. Phys. Lett. 15 327
Google Scholar
[47] Shi C M, Qin H W, Zhang Y J, Hu J F, Ju L 2014 J. Appl. Phys. 115 053907
Google Scholar
[48] Bai Y J, Deng K M, Kan E J 2015 RSC Adv. 5 18352
Google Scholar
[49] Xiao W Z, Wang L L 2014 Phys. Status Solidi B 251 1257
Google Scholar
[50] Wang X P, Zhao M W, Xia H H, Yan S S, Liu X D 2011 J. Appl. Phys. 110 033711
Google Scholar
[51] Henkelman G, Arnaldsson A, Jónsson H 2006 Comput. Mater. Sci. 36 354
Google Scholar
[52] Tang W, Sanville E, Henkelman G 2009 J. Phys. Condens. Matter 21 084204
Google Scholar
[53] Zhou J, Wang Q, Sun Q, Jena P 2010 Phys. Rev. B 81 085442
Google Scholar
[54] Osorioguillén J, Lany S, Barabash S V, Zunger A 2006 Phys. Rev. Lett. 96 107203
Google Scholar
[55] Shen L, Wu R Q, Pan H, Peng G W, Yang M, Sha Z D, Feng Y P 2008 Phys. Rev. B 78 073306
Google Scholar
-
图 1 碱金属和碱土金属掺杂GaN单层结构图 (a) 俯视图; (b) 侧视图
Fig. 1. Geometry of alkali and alkali-earth metals doped GaN monolayer: (a) Top view; (b) side view.
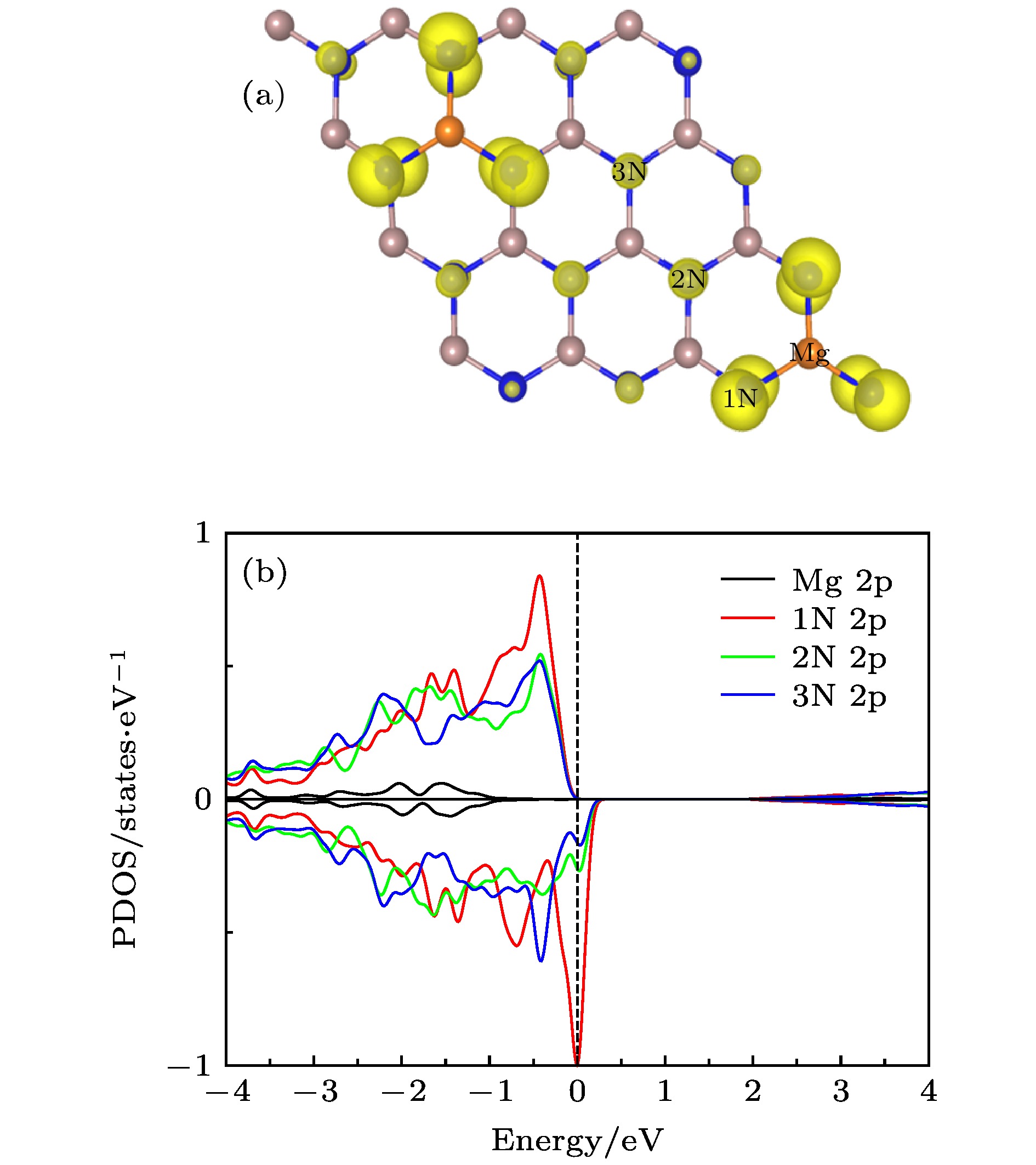
图 2 单原子掺杂GaN单层的自旋电荷密度分布图, 等值面为0.004 eV/Å (a) Li掺杂; (b) Na掺杂; (c) K掺杂; (d) Rb掺杂; (e) Be掺杂; (f) Mg掺杂; (g) Sr掺杂
Fig. 2. Spin charge density distributions of single atom doped GaN monolayer, isosurface is 0.004 eV/Å: (a) Li doping; (b) Na doping; (c) K doping; (d) Rb doping; (e) Be doping; (f) Mg doping; (g) Sr doping.
图 3 单原子掺杂GaN单层的自旋DOS和PDOS图 (a) 未掺杂; (b) Li掺杂; (c) Na掺杂; (d) K掺杂; (e) Rb掺杂; (f) Be掺杂; (g) Mg掺杂; (h) Sr掺杂
Fig. 3. Spin resolved total DOS and PDOS of GaN monolayer doped single-atom: (a) Pristine; (b) Li doping; (c) Na doping; (d) K doping; (e) Rb doping; (f) Be doping; (g) Mg doping; (h) Sr doping.
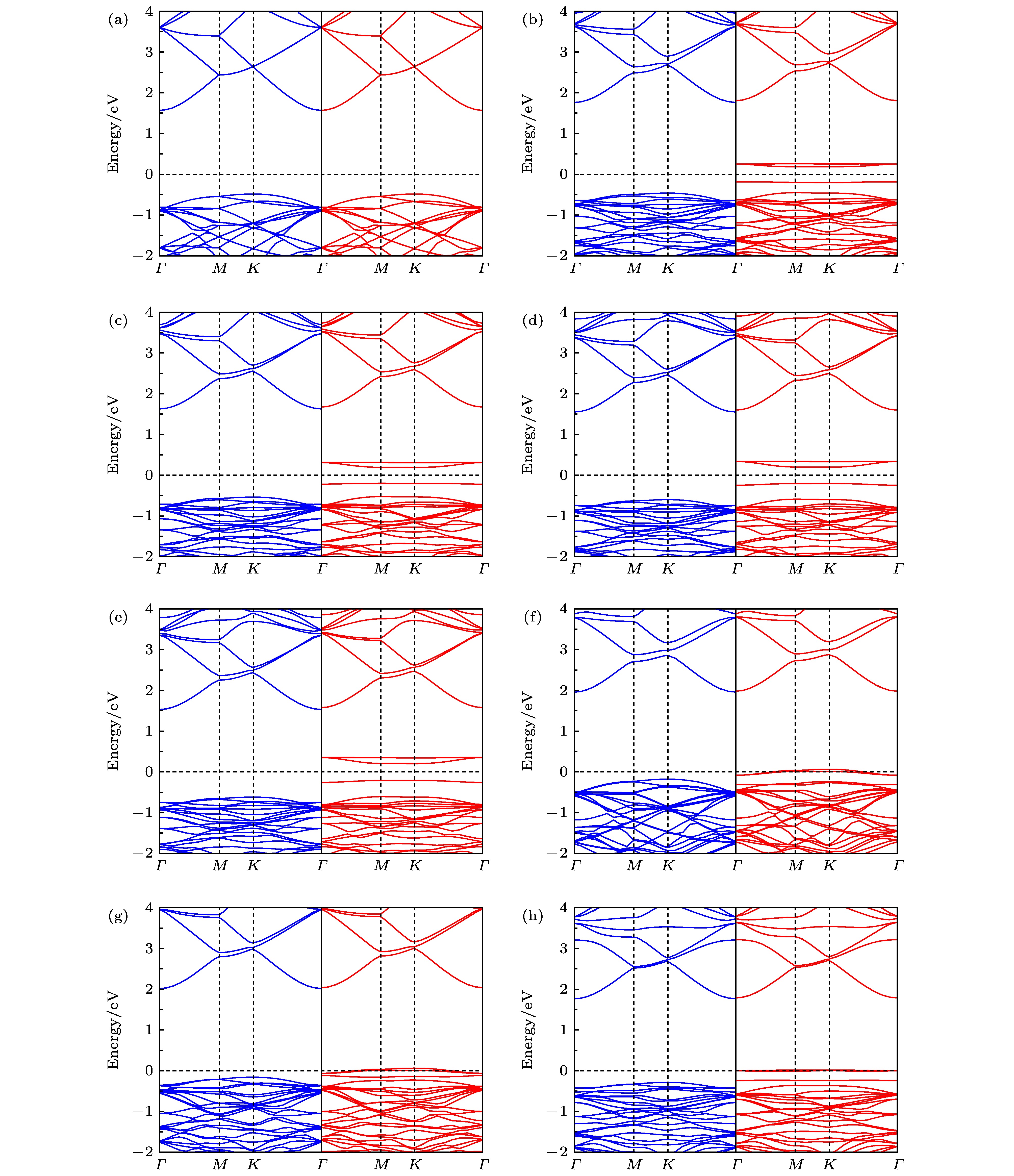
图 4 单原子掺杂GaN单层的能带结构, 图中蓝与红分别代表自旋向上与向下 (a) 未掺杂; (b) Li掺杂; (c) Na掺杂; (d) K掺杂; (e) Rb掺杂; (f) Be掺杂; (g) Mg掺杂; (h) Sr掺杂
Fig. 4. Band structures for single atom doped GaN monolayer, the blue and the red respectively represent the spin up and the spin down: (a) Pristine; (b) Li doping; (c) Na doping; (d) K doping; (e) Rb doping; (f) Be doping; (g) Mg doping; (h) Sr doping.
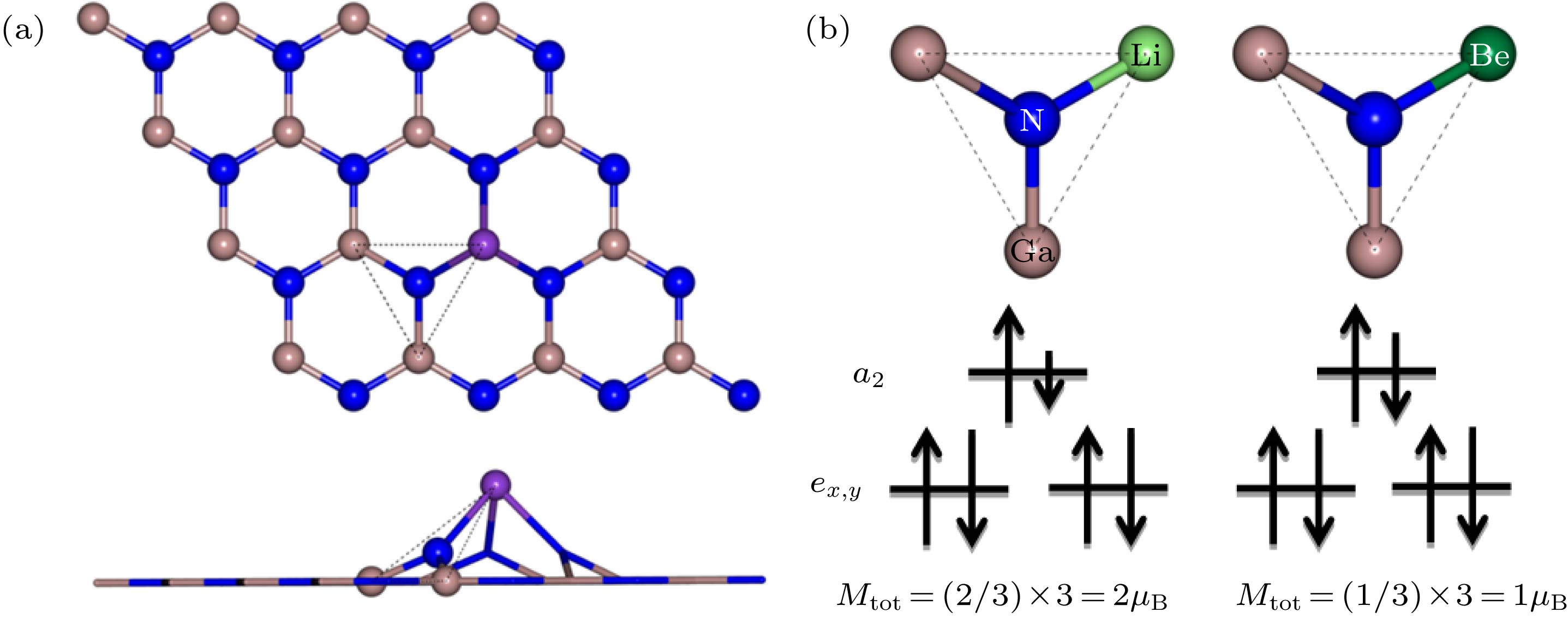
图 5 (a) 掺杂原子最近邻N原子为中心的局部结构俯视图和侧视图; (b) Li, Be掺杂原子最近邻N原子能级劈裂及电子填充示意图
Fig. 5. (a) Top and side views of a local structure centered on the nearest neighboring N atom of the doped atom; (b) schematic diagram of the energy-level splitting and electron filling of the nearest N atom of the Li, Be-doped atom.
图 6 掺杂原子最近邻N原子的p轨道态密度图 (a) 未掺杂; (b) Li掺杂; (c) Na掺杂; (d) K掺杂; (e) Rb掺杂; (f) Be掺杂; (g) Mg掺杂; (h) Sr掺杂
Fig. 6. The p-orbital DOSs of the nearest neighbor N atom of doped atom: (a) Pristine; (b) Li doping; (c) Na doping; (d) K doping; (e) Rb doping; (f) Be doping; (g) Mg doping; (h) Sr doping.
图 7 (a) Mg掺杂C4构型的自旋电荷密度分布图, 等值面为0.02 eV/Å; (b) Mg掺杂C4构型中Mg-2p, 1N-2p, 2N-2p和3N-2p的PDOS
Fig. 7. (a) Spin charge density distribution of the Mg-doped C4 configuration, the isosurface is 0.02 eV/Å; (b) PDOS of Mg-2p, 1N-2p, 2N-2p and 3N-2p in the Mg-doped C4 configuration.
表 1 两种掺杂模式的能量差
$\Delta E$ , M原子到GaN单层的距离$\Delta d$ , 优化后M—N键长dM—N, 体系形成能${E_{{\rm{form}}}}$ , 三个最近邻N原子磁矩${M_{\rm{N}}}$ 和体系总磁矩${M_{{\rm{tot}}}}$ Table 1. Energy difference
$\Delta E$ , distance from the doped atom to the GaN monolayer$\Delta d$ , optimized M—N bond length dM—N, formation energy of doped system${E_{{\rm{form}}}}$ , magnetic moment of the nearest three N atoms around the doped atom${M_{\rm{N}}}$ and total magnetic moment of doped system${M_{{\rm{tot}}}}$ .Metals $\Delta E$/eV $\Delta d$/Å dM—N/Å ${E_{{\rm{form}}}}$/eV ${M_{\rm{N}}}/{\mu _{\rm{B}}}$ ${M_{{\rm{tot}}}}/{\mu _{\rm{B}}}$ Ga-rich N-rich Li 0.295 1.127 1.972 3.522 3.303 0.543 2 Na 1.202 1.874 2.305 4.224 4.005 0.521 2 K 2.436 2.482 2.657 3.734 3.515 0.531 2 Rb 3.076 2.675 2.796 3.370 3.151 0.525 2 Be 0.000 0.000 1.679 0.582 0.363 0.218 1 Mg 0.089 0.766 1.957 3.821 3.602 0.198 1 Sr 1.956 2.031 2.382 1.324 1.105 0.239 1 
下载: 导出CSV
表 2 结构优化后两掺杂原子的距离
${d_{{\rm{M}} - {\rm{M}}}}$ , 4种构型相对稳定能${E_{{\rm{RS}}}}$ , AFM与FM的能量差$\Delta E$ , 掺杂体系总磁矩${M_{{\rm{tot}}}}$ , coupling为双M原子掺杂的GaN纳米片各构型的磁耦合态Table 2. Distance between the two doped atoms after structural optimization
${d_{{\rm{M}} - {\rm{M}}}}$ , relative stability of the four configurations${E_{{\rm{RS}}}}$ , energy difference between AFM and FM$\Delta E$ , total magnetic moment of doped system${M_{{\rm{tot}}}}$ , coupling is the magnetic coupling of various configurations of double M atom doped GaN monolayer.Metals Configurations ${d_{{\rm{M}} - {\rm{M}}}}$/Å ${E_{{\rm{RS}}}}$/eV $\Delta E$/eV ${M_{ {\rm{tot} } } }/{\mu _{\rm B}}$ Coupling Li C1 (1, 2) 3.315 0.000 0.313 4 FM C2 (1, 3) 5.663 0.318 0.049 4 FM C3 (1, 4) 6.475 0.222 0.596 4 FM C4 (1, 5) 11.215 0.222 0.034 4 FM Na C1 (1, 2) 3.662 0.000 0.308 4 FM C2 (1, 3) 5.706 0.329 0.033 4 FM C3 (1, 4) 6.475 0.216 0.481 4 FM C4 (1, 5) 11.215 0.216 0.014 4 FM K C1 (1, 2) 4.147 0.000 0.318 4 FM C2 (1, 3) 5.789 0.276 0.032 4 FM C3 (1, 4) 6.475 0.142 0.239 4 FM C4 (1, 5) 11.215 0.142 0.022 4 FM Rb C1 (1, 2) 4.326 0.000 0.322 4 FM C2 (1, 3) 5.842 0.272 0.096 4 FM C3 (1, 4) 6.475 0.137 0.240 4 FM C4 (1, 5) 11.215 0.137 0.019 4 FM Be C1 (1, 2) 3.168 0.068 0.289 2 FM C2 (1, 3) 5.597 0.000 0.000 2 FM C3 (1, 4) 6.475 0.100 0.148 2 FM C4 (1, 5) 11.215 0.100 0.119 2 FM Mg C1 (1, 2) 3.359 0.000 0.241 2 FM C2 (1, 3) 5.651 0.035 –0.003 2 FM C3 (1, 4) 6.475 0.080 0.068 2 FM C4 (1, 5) 11.215 0.079 0.168 2 FM Sr C1 (1, 2) 4.092 0.049 0.194 2 FM C2 (1, 3) 5.868 0.124 0.076 2 FM C3 (1, 4) 6.475 0.000 –0.002 0 AFM C4 (1, 5) 11.215 0.002 0.352 2 FM
下载: 导出CSV
-
[1] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[2] Srivastava P, Hembram K, Mizuseki H, Lee K R, Han S S, Kim S 2015 J. Phys. Chem. C 119 6530
Google Scholar
[3] Wang Q H, Kalantar-Zadeh K, Kis A, Coleman J N, Strano M S 2012 Nat. Nanotechnol. 7 699
Google Scholar
[4] Prinz G A 1998 Science 282 1660
Google Scholar
[5] Wolf S A, Awschalom D D, Buhrman R A, Daughton J M, von Molnar S, Roukes M L, Chtchelkanova A Y, Treger D M 2001 Science 294 1488
Google Scholar
[6] Feng B J, Ding Z J, Meng S, Yao Y G, He X Y, Cheng P, Chen L, Wu K H 2012 Nano Lett. 12 3507
Google Scholar
[7] Liu H, Neal A T, Zhu Z, Luo Z, Xu X F, Tománek D, Ye P D 2014 ACS Nano 8 4033
Google Scholar
[8] Li L K, Yu Y J, Ye G J, Ge Q Q, Ou X D, Wu H, Feng D L, Chen X H, Zhang Y B 2014 Nat. Nanotechnol. 9 372
Google Scholar
[9] Wei J W, Ma Z W, Zeng H, Wang Z Y, Wei Q, Peng P 2012 Aip Adv. 2 042141
Google Scholar
[10] Tongay S, Zhou J, Ataca C, Lo K, Matthews T S, Li J B, Grossman J C, Wu J Q 2012 Nano Lett. 12 5576
Google Scholar
[11] Song L, Ci L J, Lu H, Sorokin P B, Jin C H, Ni J, Kvashnin A G, Kvashnin D G, Lou J, Yakobson B I, Ajayan P M 2010 Nano Lett. 10 3209
Google Scholar
[12] 徐大庆, 赵子涵, 李培咸, 王超, 张岩, 刘树林, 童军 2018 67 087501
Google Scholar
Xu D Q, Zhao Z H, Li P X, Wang C, Zhang Y, Liu S L, Tong J 2018 Acta Phys. Sin. 67 087501
Google Scholar
[13] Chen G X, Wang D D, Zhang J M, Xu K W 2013 Phys. Status Solidi B 250 1510
Google Scholar
[14] Nakamura S, Mukai T, Senoh M 1994 Appl. Phys. Lett. 64 1687
Google Scholar
[15] Nakamura S 1998 Science 281 956
Google Scholar
[16] Al Balushi Z Y, Wang K, Ghosh R K, Vilá R A, Eichfeld S M, Caldwell J D, Qin X, Lin Y C, Desario P A, Stone G, Subramanian S, Paul D F, Wallace R M, Datta S, Redwing J M, Robinson J A 2016 Nat. Mater. 15 1166
Google Scholar
[17] Dietl T, Ohno H, Matsukura F, Cibert J, Ferrand D 2000 Science 287 1019
Google Scholar
[18] Overberg M E, Abernathy C R, Pearton S J, Theodoropoulou N A, McCarthy K T, Hebard A F 2001 Appl. Phys. Lett. 79 1312
Google Scholar
[19] Sasaki T, Sonoda S, Yamamoto Y, Suga K I, Shimizu S, Kindo K, Hori H 2002 J. Appl. Phys. 91 7911
Google Scholar
[20] Liu H X, Wu S Y, Singh R K, Lin G, Smith D J, Newman N, Dilley N R, Montes L, Simmonds M B 2004 Appl. Phys. Lett. 85 4076
Google Scholar
[21] Wu R Q, Peng G W, Liu L, Feng Y P, Huang Z G, Wu Q Y 2006 Appl. Phys. Lett. 89 062505
Google Scholar
[22] Fukumura T, Jin Z, Kawasaki M, Shono T, Hasegawa T, Koshihara S, Koinuma H 2001 Appl. Phys. Lett. 78 958
Google Scholar
[23] Xiao G, Wang L L, Rong Q Y, Xu H Q, Xiao W Z 2016 Comput. Mater. Sci. 124 98
Google Scholar
[24] Venkatesan M, Fitzgerald C B, Coey J M D 2004 Nature 430 630
Google Scholar
[25] Coey J M D 2005 Solid State Sci. 7 660
Google Scholar
[26] Ren J, Zhang S B, Liu P P 2019 Chin. Phys. Lett. 36 076101
Google Scholar
[27] Pan H, Yi J B, Shen L, Wu R Q, Yang J H, Lin J Y, Feng Y P, Ding J, Van L H, Yin J H 2007 Phys. Rev. Lett. 99 127201
Google Scholar
[28] Xiao G, Wang L L, Rong Q Y, Xu H Q, Xiao W Z 2016 Phys. Status Solidi B 253 1816
Google Scholar
[29] Han R L, Chen X Y, Yan Y 2017 Chin. Phys. B 26 097503
Google Scholar
[30] 潘凤春, 徐佳楠, 杨花, 林雪玲, 陈焕铭 2017 66 056101
Google Scholar
Pan F C, Xu J N, Yang H, Lin X L, Chen H M 2017 Acta Phys. Sin. 66 056101
Google Scholar
[31] 张梅玲, 陈玉红, 张材荣, 李公平 2019 68 087101
Google Scholar
Zhang M L, Chen Y H, Zhang C R, Li G P 2019 Acta Phys. Sin. 68 087101
Google Scholar
[32] Sundaresan A, Bhargavi R, Rangarajan N 2006 Phys. Rev. B 74 161306
Google Scholar
[33] Dev P, Xue Y, Zhang P 2008 Phys. Rev. Lett. 100 117204
Google Scholar
[34] Yang K S, Wu R Q, Shen L, Feng Y P, Dai Y, Huang B B 2010 Phys. Rev. B 81 125211
Google Scholar
[35] 侯清玉, 李勇, 赵春旺 2017 66 067202
Google Scholar
Hou Q Y, Li Y, Zhao C W 2017 Acta Phys. Sin. 66 067202
Google Scholar
[36] 黄毅华, 江东亮, 张辉, 陈忠明, 黄政仁 2017 66 017501
Google Scholar
Huang Y H, Jiang D L, Zhang H, Chen Z M, Huang Z R 2017 Acta Phys. Sin. 66 017501
Google Scholar
[37] Kresse G, Hafner J 1994 Phys. Rev. B 49 14251
Google Scholar
[38] Kresse G, Furthmüller J 1996 Comput. Mater. Sci. 6 15
Google Scholar
[39] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169
Google Scholar
[40] Blöchl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[41] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
Google Scholar
[42] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[43] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188
Google Scholar
[44] Şahin H, Cahangirov S, Topsakal M, Bekaroglu E, Akturk E, Senger R T, Ciraci S 2009 Phys. Rev. B 80 155453
Google Scholar
[45] Lee S M, Lee Y H, Hwang Y G, Elsner J, Porezag D, Frauenheim T 1999 Phys. Rev. B 60 7788
Google Scholar
[46] Maruska H P, Tietjen J J 1969 Appl. Phys. Lett. 15 327
Google Scholar
[47] Shi C M, Qin H W, Zhang Y J, Hu J F, Ju L 2014 J. Appl. Phys. 115 053907
Google Scholar
[48] Bai Y J, Deng K M, Kan E J 2015 RSC Adv. 5 18352
Google Scholar
[49] Xiao W Z, Wang L L 2014 Phys. Status Solidi B 251 1257
Google Scholar
[50] Wang X P, Zhao M W, Xia H H, Yan S S, Liu X D 2011 J. Appl. Phys. 110 033711
Google Scholar
[51] Henkelman G, Arnaldsson A, Jónsson H 2006 Comput. Mater. Sci. 36 354
Google Scholar
[52] Tang W, Sanville E, Henkelman G 2009 J. Phys. Condens. Matter 21 084204
Google Scholar
[53] Zhou J, Wang Q, Sun Q, Jena P 2010 Phys. Rev. B 81 085442
Google Scholar
[54] Osorioguillén J, Lany S, Barabash S V, Zunger A 2006 Phys. Rev. Lett. 96 107203
Google Scholar
[55] Shen L, Wu R Q, Pan H, Peng G W, Yang M, Sha Z D, Feng Y P 2008 Phys. Rev. B 78 073306
Google Scholar
下载:
计量
- 文章访问数: 12141
- PDF下载量: 268
- 被引次数: 0
