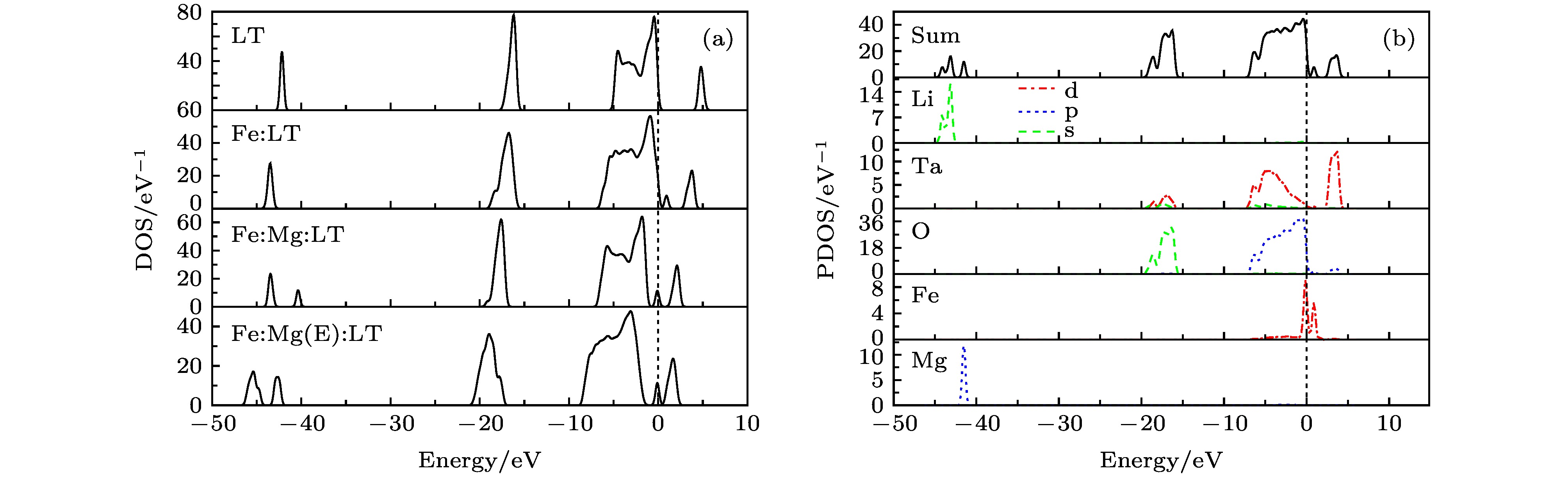
-
利用第一性原理对LiTaO3晶体以及不同Mg浓度的Fe:Mg:LiTaO3晶体的电子结构和吸收光谱进行了研究. 结果显示: 掺铁钽酸锂晶体的杂质能级主要由Fe的3d态轨道贡献, 禁带宽度为3.05 eV. 掺入镁后, 在禁带中没有新的能级产生, 掺Mg浓度小于或超过阈值(略小于6 mol%)时, 禁带宽度分别为2.72 eV和 2.45 eV. Fe:LiTaO3晶体分别在417 nm和745 nm处呈现两个吸收峰, 这两峰归结于Fe 3d分裂轨道电子的跃迁; Mg:Fe:LiTaO3晶体吸收峰强度较单掺Fe的LiTaO3晶体下降, 并略有偏移, 当掺镁浓度超过阈值时, 短波段峰移至457 nm吸收峰, 而长波段745 nm处的吸收峰消失. 研究表明: Fe离子的分裂轨道T2g, Eg跃迁所对应的吸收峰与铁离子的占位有关, Mg离子浓度达到阈值, 使Fe离子占Ta位, Eg对应的吸收峰消失. 在利用457 nm波段为功能性吸收时, 采用较高掺Mg不会对吸收产生不利影响; 在利用745 nm波段时, Fe占Li位比Fe占Ta位在存储应用中更具优势, 不宜采用高掺镁.The electronic structures and absorption spectra of LiTaO3 (LT) crystal and Fe:Mg:LiTaO3 crystal with different Mg concentrations are investigated by first-principles through using the density functional theory. The supercell crystal structures are established with 60 atoms with four models: the near-stoichiometric pure LiTaO3 crystal (LT); the iron doped LiTaO3 crystal (Fe:LT), with the charge compensation model expressed as FeLi2+-2VLi–; the iron and magnesium co-doped LiTaO3 crystal (Fe:Mg:LT), with the charge compensation model taken as FeLi2+-MgLi+-3VLi–; the other iron and magnesium co-doped LiTaO3 crystal (Fe:Mg(E):LT), with Mg ion concentration near threshold value (slightly less than 6 mol%) and taking the charge compensation model as 2MgLi+-FeTa2–. The geometry optimization results show that the total energy values of all models can achieve certain stable values, which means that the models used in this paper are very close to the actual crystal structures. In the electronic structures, the extrinsic defect energy levels in the forbidden band of Fe:LT crystal are mainly contributed from the Fe 3d orbital, and the band gap of Fe:LT about 3.05 eV is narrower than that of LT, the band gap of Fe:Mg:LT and Fe:Mg(E):LT sample are 2.72 eV and 2.45 eV respectively. The results show that the orbit of Fe 3d, Ta 5d and O 2p are superposed with each other, forming covalent bonds, which results in conduction band and valence band shifting toward low energy in iron doped LiTaO3 crystal. The Fe 3d orbit is split into Eg orbit and T2g orbit under the influence of the crystal field. There are two absorption peaks at 417 nm (2.97 eV) and 745 nm (1.66 eV) in the Fe:LiTaO3 crystal. The first one is attributed to the transfer of the T2g orbital electron to conduction band. The last one can be taken as the result of Eg electron transfer of Fe2+ in crystal. The intensities and positions of these peaks vary with the concentration of Mg ion. Specially, with the concentration of Mg ion attaining the threshold value, the peak at 745 nm disappears, and the other peak moves slightly to 457 nm (2.71 eV). With the Mg ion concentration at the threshold value, the Fe ions can occupy Ta positions. This occupying condition makes the Eg orbital energy change greatly compared with the scenario in the FeLi condition, and it affects hardly the T2g orbital energy. So, if the absorption nearby 745 nm waveband can be taken as the useful process in holographic storage application, it is better to take smaller concentration of Mg ions (less than threshold value). On the other hand, nearby 457 nm waveband, concentration of Mg ions can be chosen as a large value.
-
Keywords:
- LiTaO3 crystal /
- Fe and Mg co-doped /
- electronic structure /
- absorption spectrum /
- first-principles
[1] Steinberg I S, Kalabin I E, Tverdokhleb P E 2009 Appl. Phys. B 95 407
Google Scholar
[2] Wang K M, Chen F, Hu H, Zhang J H, Lu Fei, Shi B R, Lu Q M, Ma C Q 2001 Opt. Commun. 196 215
Google Scholar
[3] Kip D 1998 Appl. Phys. B 67 131
Google Scholar
[4] Hossain A, Rashid M H 1991 Ind. Appl. 27 824
Google Scholar
[5] Gualtieri J G, Kosinski J A, Ballato A 1994 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 41 53
Google Scholar
[6] Meyn J P, Fejer M M 1997 Opt. Lett. 22 1214
Google Scholar
[7] Mizuuchi K, Yamamoto K, Kato M 1997 Appl. Phys. Lett. 70 1201
Google Scholar
[8] Krätzig E, Orlowski R 1978 Appl. Phys. 15 133
Google Scholar
[9] Fang S Q, Wang B, Zhang T, Ling F R, Wang R 2006 Opt. Mater. 28 207
Google Scholar
[10] Fang S Q, Ma D C, Zhang T, Ling F R, Wang B 2006 Opt. 117 72
[11] Tsuya H 1975 J. Appl. Phys. 46 4323
Google Scholar
[12] Wang R, Sun X D, Xu W S, Zhen X H 2000 High Technol. Lett. 6 52
[13] Hsu W T, Chen Z B, Wu C C, Choubey R K, Lan C W 2012 Mater. 5 227
Google Scholar
[14] Song Y J, Zhang Q H, Shen X, Ni X D, Yao Y, Yu R C 2014 Chin. Phys. Lett. 31 017501
Google Scholar
[15] Gorelik V S, Sidorov N V, Vodchits A I 2017 Phys. Wave Phenom. 25 10
Google Scholar
[16] Cheng B, Qin H W, Zhang Z L, Liu W K, Miao T T, Xie J H, Liu L, Zhou G J, Hu J F 2018 J. Mater. Chem. C 6 11608
Google Scholar
[17] Abrahams S C, Buehler E, Hamilton W C, Laplaca S J 1973 J. Phys. Chem. Solids 34 521
Google Scholar
[18] Segall M D, Lindan P J D, Probert M J, Pickard C J, Hasnip P J, Clark S J, Payne M C 2002 J. Phys. Condens. Matter 14 2717
Google Scholar
[19] Vanderbilt D 1990 Phys. Rev. B 41 7892
Google Scholar
[20] Tian F H, Liu C B 2006 J. Phys. Chem. B 110 17866
Google Scholar
[21] 赵佰强, 张耘, 邱晓燕, 王学维 2015 64 124210
Google Scholar
Zhao B Q, Zhang Y, Qiu X Y, Wang X W 2015 Acta Phys. Sin. 64 124210
Google Scholar
[22] Çabuk S, Mamedov A 1999 J. Opt. A: Pure Appl. Opt. 1 424
Google Scholar
[23] 张学军, 高攀, 柳清菊 2010 59 4930
Google Scholar
Zhang X J, Gao P, Liu Q J 2010 Acta Phys. Sin. 59 4930
Google Scholar
[24] 沈学础 2002 半导体光谱和光学性质 (第二版) (北京:科学出版社) 第 76 页
Shen X C 2002 Spectra and Optical Properties of Semiconductors (2nd Ed.) (Beijing: Science Press) p76 (in Chinese)
[25] 苏玉长, 肖立华, 伏云昌, 张鹏飞, 彭平 2011 中国科学 G 辑: 物理学 力学 天文学 41 58
Su Y C, Xiao L H, Fu Y C, Zhang P F, Peng P 2011 Sci. China Ser. G 41 58
[26] 王雪艳, 郑建邦, 李晓江, 曹崇德 2016 光子学报 45 0616001
Wang X Y, Zheng J B, Li X J, Cao C D 2016 Acta Photon. Sin. 45 0616001
[27] Vormann H, Krätzig E 1984 Solid State Commun. 49 843
Google Scholar
[28] Buse K, Jermann F, Kräzig E 1993 Ferroelectrics 141 197
Google Scholar
[29] 孔勇发, 李兵, 陈云琳, 黄自恒, 陈绍林, 张玲, 刘士国, 许京军, 阎文博, 刘宏德, 王岩, 谢翔, 张万林, 张光寅 2003 红外与毫米波学报 22 40
Google Scholar
Kong Y F, Li B, Chen Y L, Huang Z H, Chen S L, Zhang L, Liu S G, Xu J J, Yan W B, Liu H D, Wang Y, Xie X, Zhang W L, Zhang G Y 2003 J. Infrared Millim. Waves 22 40
Google Scholar
[30] Mok F H, Burr G W, Psaltis D 1996 Opt. Lett. 21 896
Google Scholar
[31] Yang Y P, Psaltis D, Luennemmann M, Berben D, Hartwig U, Buse K 2003 J. Opt. Soc. Am. B 20 1491
Google Scholar
-
图 3 能带结构图 (a) LT; (b) Fe:LT; (c) Fe:Mg:LT; (d) Fe:Mg(E):LT
Fig. 3. Band structures of (a) LT; (b) Fe:LT; (c) Fe:Mg:LT; (d) Fe:Mg(E):LT.
图 4 晶体态密度图 (a) LT及不同掺Mg浓度的Fe:Mg:LT晶体态密度图; (b) Fe:Mg:LT晶体分态密度图
Fig. 4. Density of states of crystals: (a) Density of states of LT and Fe:Mg:LT crystals; (b) partial density of states of Fe:Mg:LT crystals.
图 5 晶体禁带附近分态密度 (a) Fe:LT; (b) Fe:Mg:LT; (c) Fe:Mg(E):LT
Fig. 5. Partial density of states near the forbidden band: (a) Fe:LT; (b) Fe:Mg:LT (c) Fe:Mg(E):LT.
表 1 LT晶体内各原子坐标
Table 1. Coordinates of atoms within LT crystal.
Atom Oxidation state X/nm Y/nm Z/nm Li 1 0 0 0.2821 Ta 5 0 0 0 O –2 0.0534 0.3396 0.0695 
下载: 导出CSV
表 2 LT 晶格常数的几何优化值与实验值
Table 2. Geometry optimization result and experiment values of LT crystal.
Lattice parameter a/nm b/nm c/nm V/nm3 Experimental value 1.0308 0.5154 1.3863 637.83 × 10–3 Optimization result 1.0521 0.5260 1.4127 677.19 × 10–3
下载: 导出CSV
-
[1] Steinberg I S, Kalabin I E, Tverdokhleb P E 2009 Appl. Phys. B 95 407
Google Scholar
[2] Wang K M, Chen F, Hu H, Zhang J H, Lu Fei, Shi B R, Lu Q M, Ma C Q 2001 Opt. Commun. 196 215
Google Scholar
[3] Kip D 1998 Appl. Phys. B 67 131
Google Scholar
[4] Hossain A, Rashid M H 1991 Ind. Appl. 27 824
Google Scholar
[5] Gualtieri J G, Kosinski J A, Ballato A 1994 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 41 53
Google Scholar
[6] Meyn J P, Fejer M M 1997 Opt. Lett. 22 1214
Google Scholar
[7] Mizuuchi K, Yamamoto K, Kato M 1997 Appl. Phys. Lett. 70 1201
Google Scholar
[8] Krätzig E, Orlowski R 1978 Appl. Phys. 15 133
Google Scholar
[9] Fang S Q, Wang B, Zhang T, Ling F R, Wang R 2006 Opt. Mater. 28 207
Google Scholar
[10] Fang S Q, Ma D C, Zhang T, Ling F R, Wang B 2006 Opt. 117 72
[11] Tsuya H 1975 J. Appl. Phys. 46 4323
Google Scholar
[12] Wang R, Sun X D, Xu W S, Zhen X H 2000 High Technol. Lett. 6 52
[13] Hsu W T, Chen Z B, Wu C C, Choubey R K, Lan C W 2012 Mater. 5 227
Google Scholar
[14] Song Y J, Zhang Q H, Shen X, Ni X D, Yao Y, Yu R C 2014 Chin. Phys. Lett. 31 017501
Google Scholar
[15] Gorelik V S, Sidorov N V, Vodchits A I 2017 Phys. Wave Phenom. 25 10
Google Scholar
[16] Cheng B, Qin H W, Zhang Z L, Liu W K, Miao T T, Xie J H, Liu L, Zhou G J, Hu J F 2018 J. Mater. Chem. C 6 11608
Google Scholar
[17] Abrahams S C, Buehler E, Hamilton W C, Laplaca S J 1973 J. Phys. Chem. Solids 34 521
Google Scholar
[18] Segall M D, Lindan P J D, Probert M J, Pickard C J, Hasnip P J, Clark S J, Payne M C 2002 J. Phys. Condens. Matter 14 2717
Google Scholar
[19] Vanderbilt D 1990 Phys. Rev. B 41 7892
Google Scholar
[20] Tian F H, Liu C B 2006 J. Phys. Chem. B 110 17866
Google Scholar
[21] 赵佰强, 张耘, 邱晓燕, 王学维 2015 64 124210
Google Scholar
Zhao B Q, Zhang Y, Qiu X Y, Wang X W 2015 Acta Phys. Sin. 64 124210
Google Scholar
[22] Çabuk S, Mamedov A 1999 J. Opt. A: Pure Appl. Opt. 1 424
Google Scholar
[23] 张学军, 高攀, 柳清菊 2010 59 4930
Google Scholar
Zhang X J, Gao P, Liu Q J 2010 Acta Phys. Sin. 59 4930
Google Scholar
[24] 沈学础 2002 半导体光谱和光学性质 (第二版) (北京:科学出版社) 第 76 页
Shen X C 2002 Spectra and Optical Properties of Semiconductors (2nd Ed.) (Beijing: Science Press) p76 (in Chinese)
[25] 苏玉长, 肖立华, 伏云昌, 张鹏飞, 彭平 2011 中国科学 G 辑: 物理学 力学 天文学 41 58
Su Y C, Xiao L H, Fu Y C, Zhang P F, Peng P 2011 Sci. China Ser. G 41 58
[26] 王雪艳, 郑建邦, 李晓江, 曹崇德 2016 光子学报 45 0616001
Wang X Y, Zheng J B, Li X J, Cao C D 2016 Acta Photon. Sin. 45 0616001
[27] Vormann H, Krätzig E 1984 Solid State Commun. 49 843
Google Scholar
[28] Buse K, Jermann F, Kräzig E 1993 Ferroelectrics 141 197
Google Scholar
[29] 孔勇发, 李兵, 陈云琳, 黄自恒, 陈绍林, 张玲, 刘士国, 许京军, 阎文博, 刘宏德, 王岩, 谢翔, 张万林, 张光寅 2003 红外与毫米波学报 22 40
Google Scholar
Kong Y F, Li B, Chen Y L, Huang Z H, Chen S L, Zhang L, Liu S G, Xu J J, Yan W B, Liu H D, Wang Y, Xie X, Zhang W L, Zhang G Y 2003 J. Infrared Millim. Waves 22 40
Google Scholar
[30] Mok F H, Burr G W, Psaltis D 1996 Opt. Lett. 21 896
Google Scholar
[31] Yang Y P, Psaltis D, Luennemmann M, Berben D, Hartwig U, Buse K 2003 J. Opt. Soc. Am. B 20 1491
Google Scholar
下载:
计量
- 文章访问数: 9401
- PDF下载量: 82
- 被引次数: 0
