-
建立了铁电/铁磁双层膜模型, 铁电层的电矩用连续标量描述, 而铁磁层的自旋应用经典矢量描述. 利用蒙特卡罗方法模拟了体系的热力学性质和极化、磁化行为. 给出了零场下体系的内能、比热、极化和磁化随温度变化的关系, 并分别研究了体系在外磁场和外电场下的极化和磁化行为. 模拟结果表明, 双层膜体系的内能、比热、极化和磁化性质因层间耦合系数的不同而明显不同, 当界面耦合较弱时, 双层膜表现出各自的热力学性质, 当层间耦合增强到一定程度时, 双层膜耦合为一个整体, 表现出统一的热力学性质. 该双层膜在外场中形成电滞回线和磁滞回线, 并表现出偏置特性, 界面耦合强度和温度影响滞后回线和偏置现象.
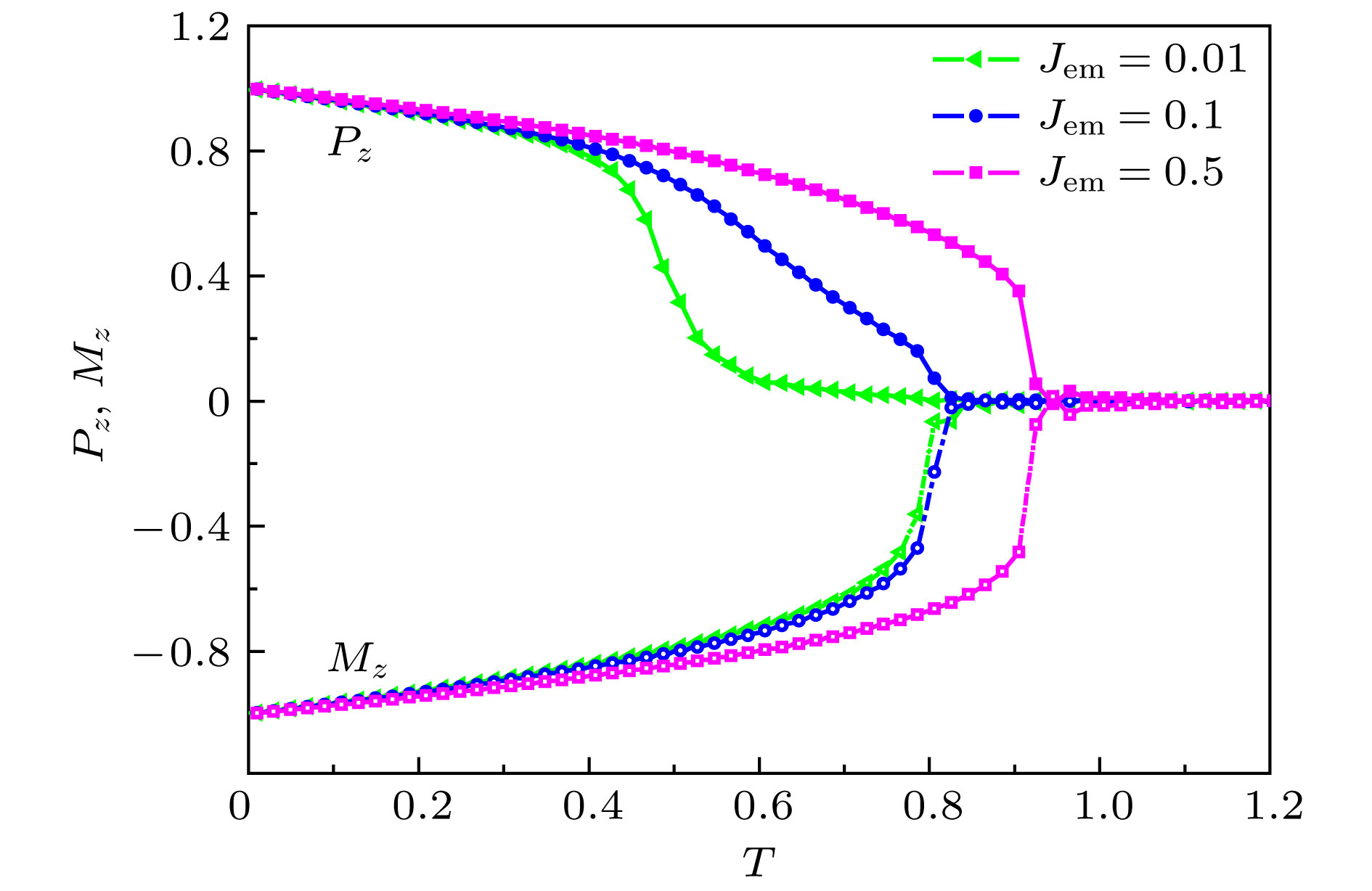
A ferroelectric/ferromagnetic bilayer film model is established. The electric moment of ferroelectric layer is described by continuous scalars, and the spins of ferromagnetic layer are described by classical vectors. The thermodynamic properties, polarization and magnetization behavior are simulated by using Monte Carlo method. The temperature dependence of internal energy, specific heat, polarization and magnetization of the system under zero field are given, and the polarization and magnetization behavior of the system under an external magnetic field and under an external electric field are studied respectively. Simulation results show that the values of internal energy, specific heat, polarization and magnetization of the bilayer films under no action of external field are obviously different from each other due to the fact that their interlayer coupling coefficients are different. When the interfacial coupling is weak (Jem = 0.01), the bilayer films exhibit their own thermodynamic properties. The interaction between ferroelectric layer and ferromagnetic layer increases with the increase of interlayer coupling coefficient. When the interfacial coupling increases to a certain extent (Jem = 0.5), the bilayer film is coupled into a whole and exhibits a uniform thermodynamic behavior. The phase transition temperature of the system increases significantly. In an external magnetic field, the ferromagnetic layer shows hysteresis behavior, and the ferroelectric layer also shows hysteresis behavior. At relatively low temperature (T = 0.08), the hysteresis loop of ferromagnetic layer and ferroelectric layer exhibit bias behavior, the area of hysteresis loop of ferroelectric layer is small when the interfacial coupling is weak. With the increase of interfacial coupling, the phenomenon of bias is more obvious, and the area of hysteresis loop of ferroelectric layer also increases significantly. When the interfacial coupling reaches Jem = 0.75, the polarization behavior of the ferroelectric layer fully responds to the magnetization behavior of the ferromagnetic layer, and neither the bias phenomenon of the ferromagnetic layer nor the bias phenomenon of the ferroelectric layer is still existent. As temperature increases (T = 0.4), the phenomenon of bias disappears even if the interlayer coupling is weak. In an external electric field, the hysteresis behavior of ferromagnetic layer and the hysteresis behavior of ferroelectric layer are similar to those in an external magnetic field. The difference is that the bias phenomenon of the bilayer film still exists for weak interfacial coupling at relatively high temperature (T = 0.4). The theoretical results are in good agreement with the experimental results reported in the literature. -
Keywords:
- polarization /
- magnetization /
- loop /
- bias
[1] Schmid H 1994 Ferroelectrics 162 317
Google Scholar
[2] Fiebig M 2005 J. Phys. D: Appl. Phys. 38 R123
Google Scholar
[3] Eerenstein W, Mathur N D, Scott J F 2006 Nature 442 759
Google Scholar
[4] Nan T, Hui Y, Rinaldi M, Sun N X 2013 Sci. Rep. 3 1985
Google Scholar
[5] O'Handley R C, Huang J K, Bono D C, Simon J 2008 IEEE Sens. J. 8 57
Google Scholar
[6] 南策文 2015 中国科学: 技术科学 45 339
Google Scholar
Nan C W 2015 Sci. Sin. Tech. 45 339
Google Scholar
[7] Zheng H, Wang J, Lofland S E, Ma Z, Mohaddes-Ardabili L, Zhao T, Salamanca-Riba L, Shinde S R, Ogale S B, Bai F, Viehland D, Jia Y, Schlom D G, Wuttig M, Roytburd A, Ramesh R 2004 Science 303 661
Google Scholar
[8] Ryu H, Murugavel P, Lee J H, Chae S C, Noh T W 2006 Appl. Phys. Lett. 89 102907
Google Scholar
[9] Deng C Y, Zhang Y, Ma J, Lin Y H, Nan C W 2007 J. Appl. Phys. 102 074114
Google Scholar
[10] Park J H, Jang H M, Kim H S, Park C G, Lee S G 2008 Appl. Phys. Lett. 92 062908
Google Scholar
[11] Zavaliche F, Zheng H, Mohaddesardabili L, Yang S Y, Zhan Q, Shafer P, Reilly E, Chopdekar R, Jia Y, Wright P, Schlom D G, Suzuki Y, Ramesh R 2005 Nano Lett. 5 1793
Google Scholar
[12] Greve H, Woltermann E, Quenzer H J, Wagner B, Quandt E 2010 Appl. Phys. Lett. 2010 96 182501
Google Scholar
[13] He H C, Zhou J P, Wang J, Nan C W 2006 Appl. Phys. Lett. 89 052904
Google Scholar
[14] Leufke P M, Kruk R, Brand R A, Hahn H 2013 Phys. Rev. B 87 094416
Google Scholar
[15] Zurbuchen M A, Wu T, Saha S, Mitchell J 2005 Appl. Phys. Lett. 87 232908
Google Scholar
[16] 李永超, 周航, 潘丹峰, 张浩, 万建国 2015 64 097701
Google Scholar
Li Y C, Zhou H, Pan D F, Zhang H, Wan J G 2015 Acta Phys. Sin. 64 097701
Google Scholar
[17] 王建元, 白健英, 罗炳成, 王拴虎, 金克新, 陈长乐 2018 67 017701
Google Scholar
Wang J Y, Bai J Y, Luo B C, Wang S H, Jin K X, Chen C L 2018 Acta Phys. Sin. 67 017701
Google Scholar
[18] Ramana E V, Zavasnik J, Graca M P F, Valente M A 2016 J. Appl. Phys. 120 074108
Google Scholar
[19] Liu G, Nan C W, Xu Z K, Chen H 2005 J. Phys. D: Appl. Phys. 38 2321
Google Scholar
[20] Duan C G, Velev J P, Sabirianov R F, Zhu Z, Jaswal S S, Tsymbal E Y 2008 Phys. Rev. Lett. 101 137201
Google Scholar
[21] Nan C W, Liu G, Lin Y H, Chen H 2005 Phys. Rev. Lett. 94 197203
Google Scholar
[22] Sukhov A, Jia C L, Horley P P, Berakdar J 2010 J. Phys.: Condens. Matter 22 352201
Google Scholar
-
图 1 FE/FM双层膜结构示意图
Fig. 1. Schematic of the ferroelectric/ferromagnetic double layer film.
图 2 自发极化和磁化随温度变化曲线
Fig. 2. Temperature dependencies of the spontaneous polarization and spontaneous magnetization of the system.
图 3 (a)内能和(b)比热随温度的变化
Fig. 3. Temperature dependencies of (a) energy and (b) specific heat.
图 4 双层膜极化率(a)和磁化率(b)随温度的变化
Fig. 4. Temperature dependencies of (a) electric susceptibility and (b) magnetic susceptibility.
图 5 双层膜在外磁场中的滞后回线(
$T = 0.08$ ) (a)${J_{{\rm{em}}}} = 0.01$ ,$0.1$ ,$0.5$ ; (b)${J_{{\rm{em}}}} = 1.0$ Fig. 5. Polarization and magnetization loops in external magnetic field at
$T = 0.08$ : (a)${J_{{\rm{em}}}} = 0.01$ ,$0.1$ ,$0.5$ ; (b)${J_{{\rm{em}}}} = 1.0$ .
图 6 双层膜在外磁场中的滞后回线(
$T = 0.4$ ,${J_{{\rm{em}}}} = 0.01$ ,$0.1$ ,$0.3$ ,$0.5$ )Fig. 6. Polarization and magnetization loops in external magnetic field at
$T = 0.4$ ,${J_{{\rm{em}}}} = 0.01$ ,$0.1$ ,$0.3$ ,$0.5$ .
图 7 双层膜在外电场中的滞后回线 (a)
$T = 0.08$ ,${J_{{\rm{em}}}} = 0.01$ ,$0.1$ ; (b)$T = 0.08$ ,${J_{{\rm{em}}}} = 0.5$ ,$1.0$ ; (c)$T = 0.4$ ,${J_{{\rm{em}}}} = 0.01$ ,$0.1$ ; (d)$T = 0.4$ ,${J_{{\rm{em}}}} = 0.3$ ,$0.5$ Fig. 7. Magnetization and polarization loops in external electric field: (a)
$T = 0.08$ ,${J_{{\rm{em}}}} = 0.01$ ,$0.1$ ; (b)$T = 0.08$ ,${J_{{\rm{em}}}} = 0.5$ ,$1.0$ ; (c)$T = 0.4$ ,${J_{{\rm{em}}}} = 0.01$ ,$0.1$ ; (d)$T = 0.4$ ,${J_{{\rm{em}}}} = 0.3$ ,$0.5$ . -
[1] Schmid H 1994 Ferroelectrics 162 317
Google Scholar
[2] Fiebig M 2005 J. Phys. D: Appl. Phys. 38 R123
Google Scholar
[3] Eerenstein W, Mathur N D, Scott J F 2006 Nature 442 759
Google Scholar
[4] Nan T, Hui Y, Rinaldi M, Sun N X 2013 Sci. Rep. 3 1985
Google Scholar
[5] O'Handley R C, Huang J K, Bono D C, Simon J 2008 IEEE Sens. J. 8 57
Google Scholar
[6] 南策文 2015 中国科学: 技术科学 45 339
Google Scholar
Nan C W 2015 Sci. Sin. Tech. 45 339
Google Scholar
[7] Zheng H, Wang J, Lofland S E, Ma Z, Mohaddes-Ardabili L, Zhao T, Salamanca-Riba L, Shinde S R, Ogale S B, Bai F, Viehland D, Jia Y, Schlom D G, Wuttig M, Roytburd A, Ramesh R 2004 Science 303 661
Google Scholar
[8] Ryu H, Murugavel P, Lee J H, Chae S C, Noh T W 2006 Appl. Phys. Lett. 89 102907
Google Scholar
[9] Deng C Y, Zhang Y, Ma J, Lin Y H, Nan C W 2007 J. Appl. Phys. 102 074114
Google Scholar
[10] Park J H, Jang H M, Kim H S, Park C G, Lee S G 2008 Appl. Phys. Lett. 92 062908
Google Scholar
[11] Zavaliche F, Zheng H, Mohaddesardabili L, Yang S Y, Zhan Q, Shafer P, Reilly E, Chopdekar R, Jia Y, Wright P, Schlom D G, Suzuki Y, Ramesh R 2005 Nano Lett. 5 1793
Google Scholar
[12] Greve H, Woltermann E, Quenzer H J, Wagner B, Quandt E 2010 Appl. Phys. Lett. 2010 96 182501
Google Scholar
[13] He H C, Zhou J P, Wang J, Nan C W 2006 Appl. Phys. Lett. 89 052904
Google Scholar
[14] Leufke P M, Kruk R, Brand R A, Hahn H 2013 Phys. Rev. B 87 094416
Google Scholar
[15] Zurbuchen M A, Wu T, Saha S, Mitchell J 2005 Appl. Phys. Lett. 87 232908
Google Scholar
[16] 李永超, 周航, 潘丹峰, 张浩, 万建国 2015 64 097701
Google Scholar
Li Y C, Zhou H, Pan D F, Zhang H, Wan J G 2015 Acta Phys. Sin. 64 097701
Google Scholar
[17] 王建元, 白健英, 罗炳成, 王拴虎, 金克新, 陈长乐 2018 67 017701
Google Scholar
Wang J Y, Bai J Y, Luo B C, Wang S H, Jin K X, Chen C L 2018 Acta Phys. Sin. 67 017701
Google Scholar
[18] Ramana E V, Zavasnik J, Graca M P F, Valente M A 2016 J. Appl. Phys. 120 074108
Google Scholar
[19] Liu G, Nan C W, Xu Z K, Chen H 2005 J. Phys. D: Appl. Phys. 38 2321
Google Scholar
[20] Duan C G, Velev J P, Sabirianov R F, Zhu Z, Jaswal S S, Tsymbal E Y 2008 Phys. Rev. Lett. 101 137201
Google Scholar
[21] Nan C W, Liu G, Lin Y H, Chen H 2005 Phys. Rev. Lett. 94 197203
Google Scholar
[22] Sukhov A, Jia C L, Horley P P, Berakdar J 2010 J. Phys.: Condens. Matter 22 352201
Google Scholar
下载:
计量
- 文章访问数: 6632
- PDF下载量: 0
- 被引次数: 0
