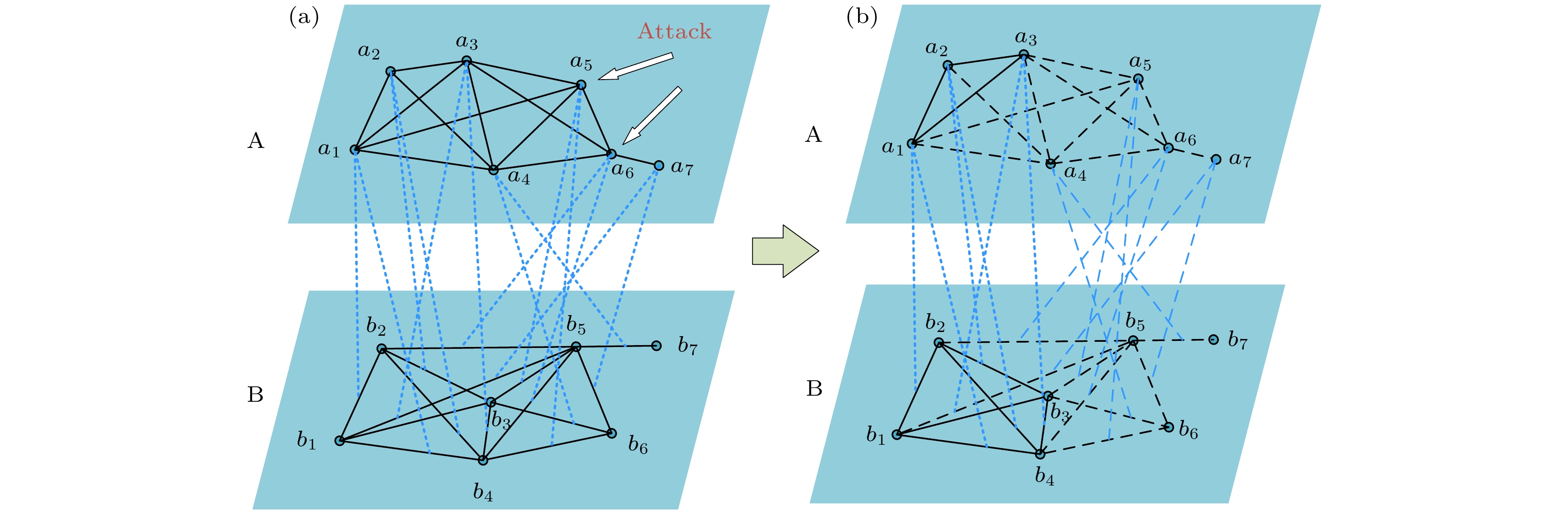
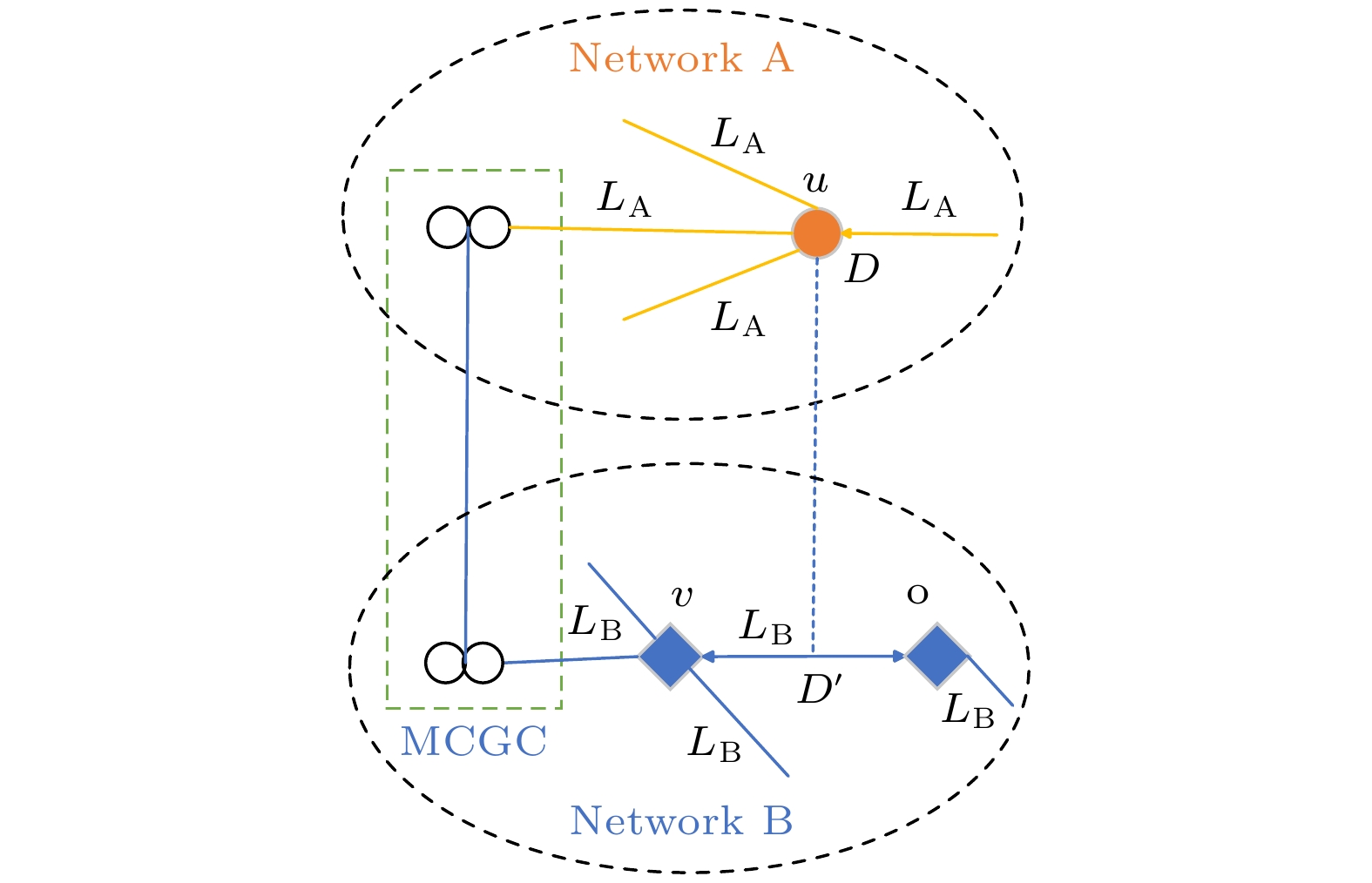
-
Existing research on interdependent networks defines network functionality as being entirely on nodes or on edges, which means interdependence between nodes and nodes, or interdependence between edges and edges. However, the reality is not characterized solely by interdependence between functionalities of individual elements, which means that it is not entirely a single-element coupled network. In some cases, nodes and edges are interdependent. Considering this reality, a binary interdependent network model with node and edge coupling (BINNEC), where both nodes and edges are interdependent, is proposed in this work. In this model, nodes in network A randomly depend on multiple edges in network B, forming edge-dependent clusters. Additionally, a failure tolerance parameter, denoted as
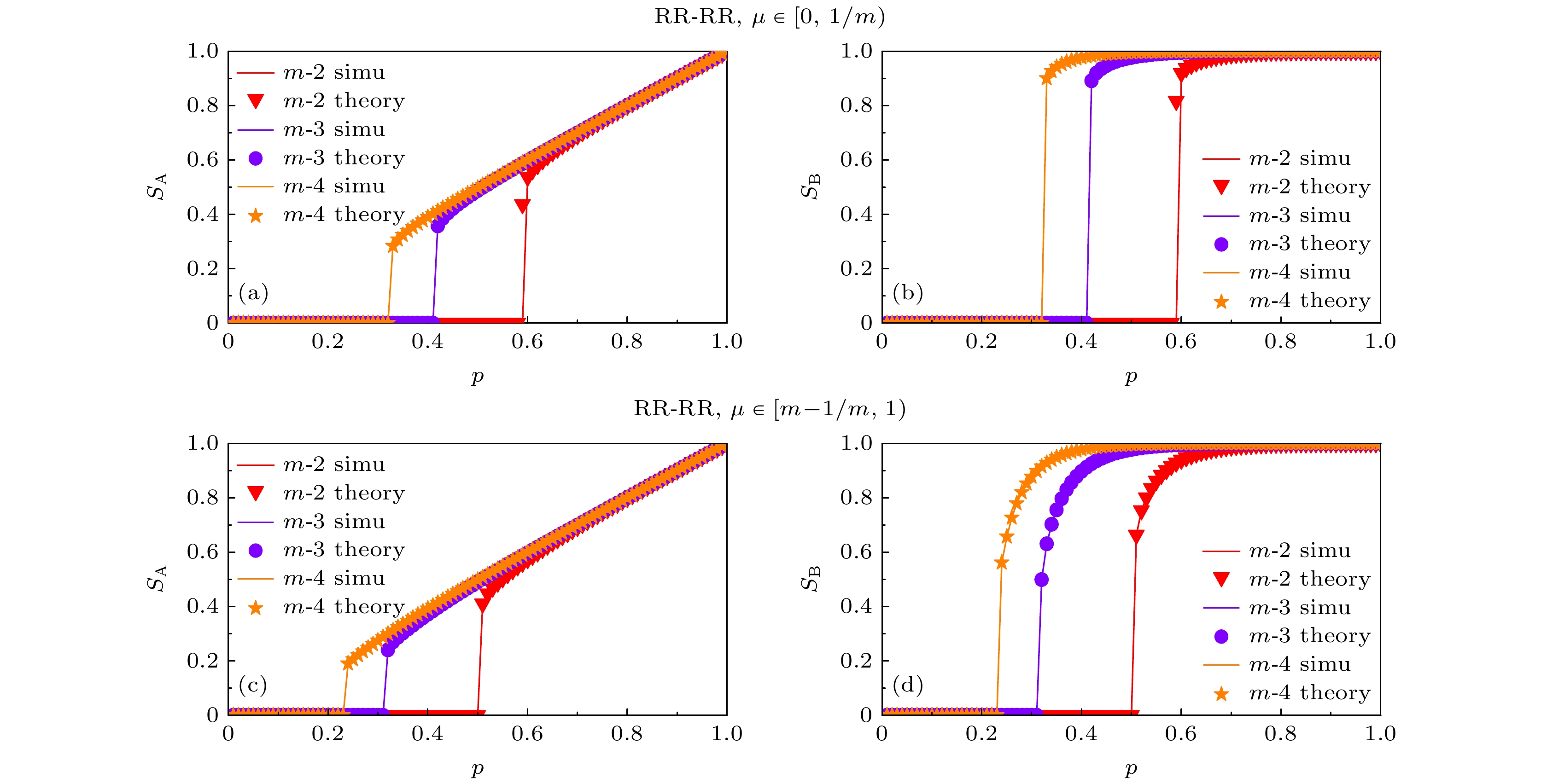
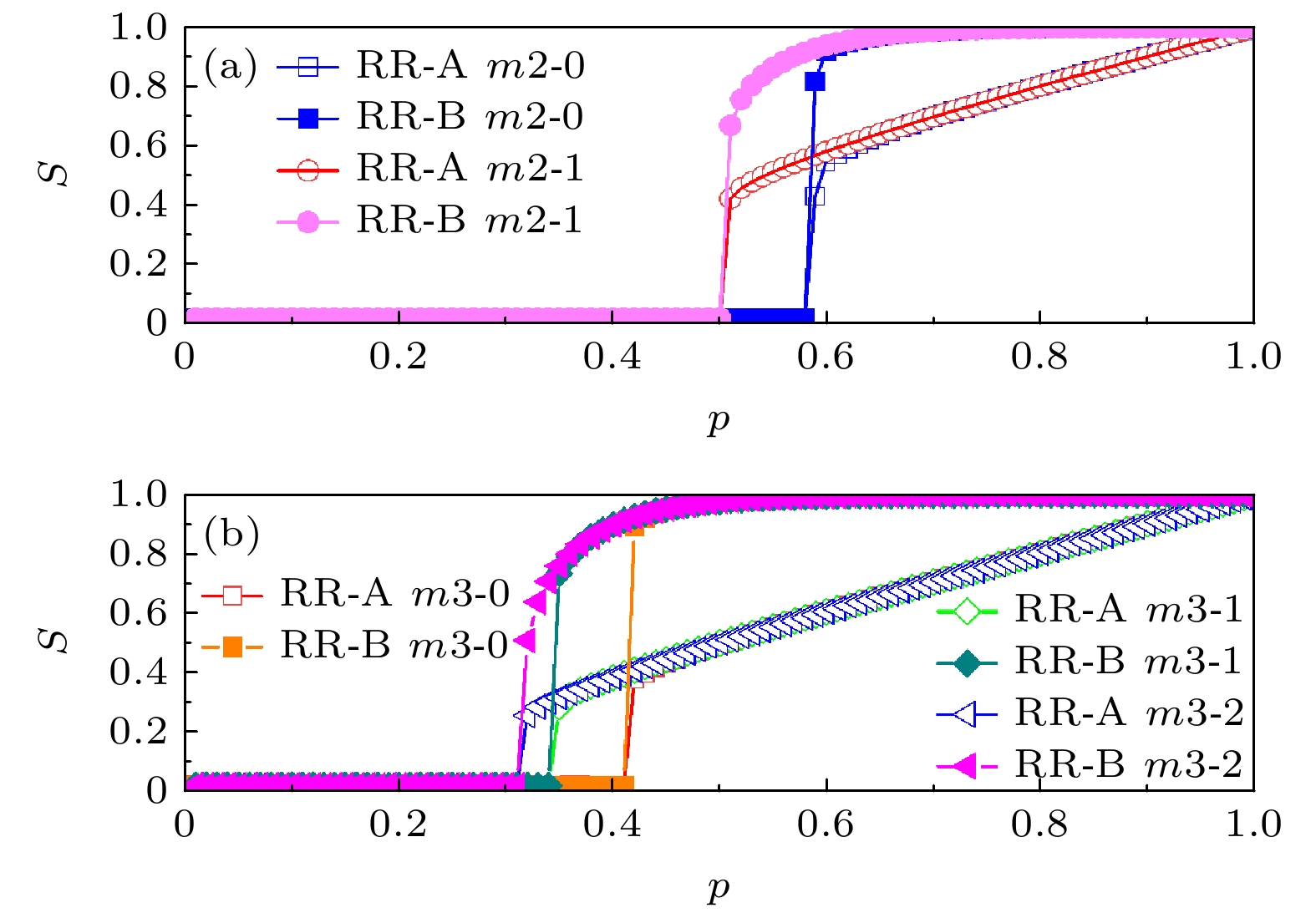
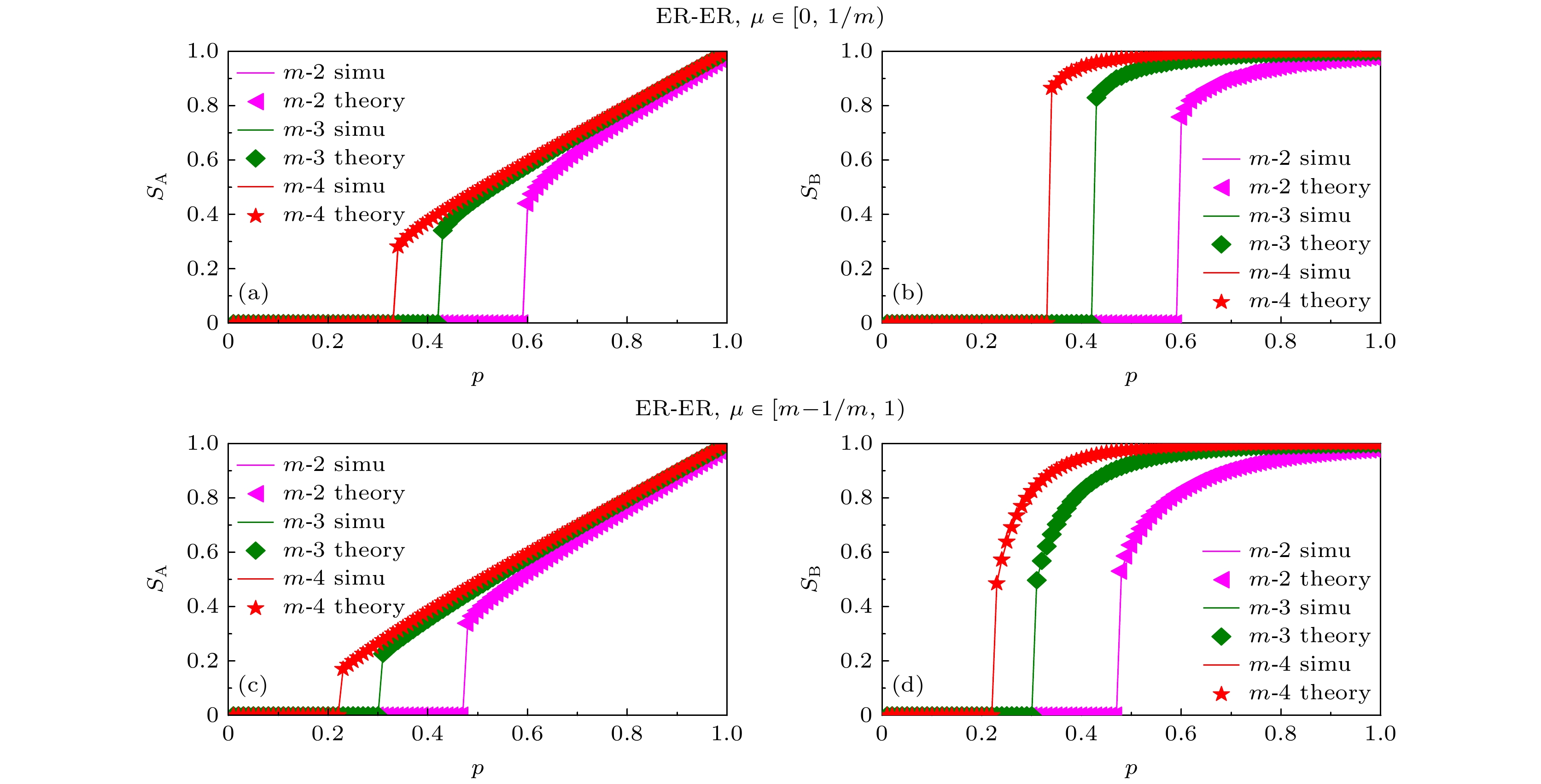
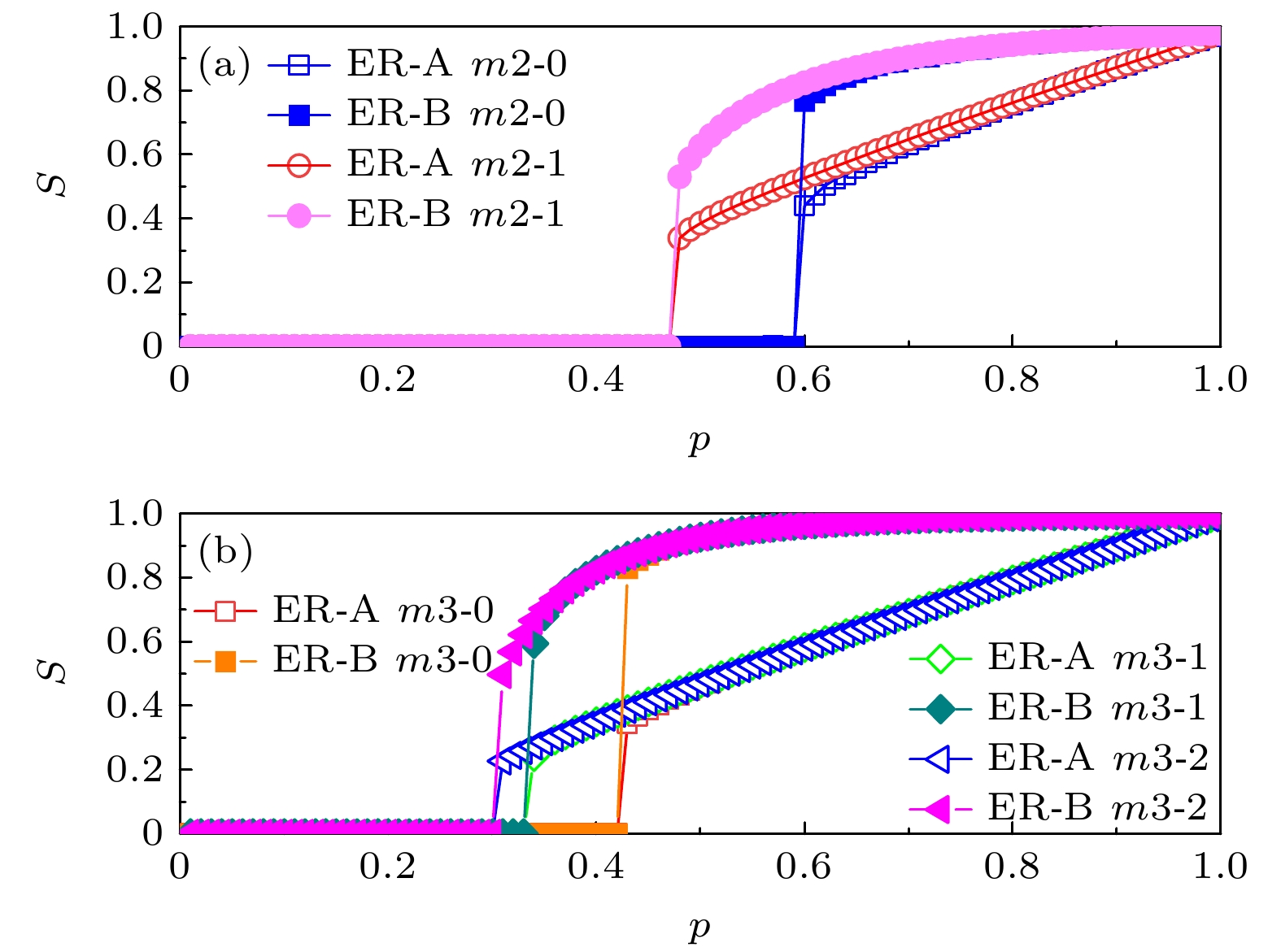
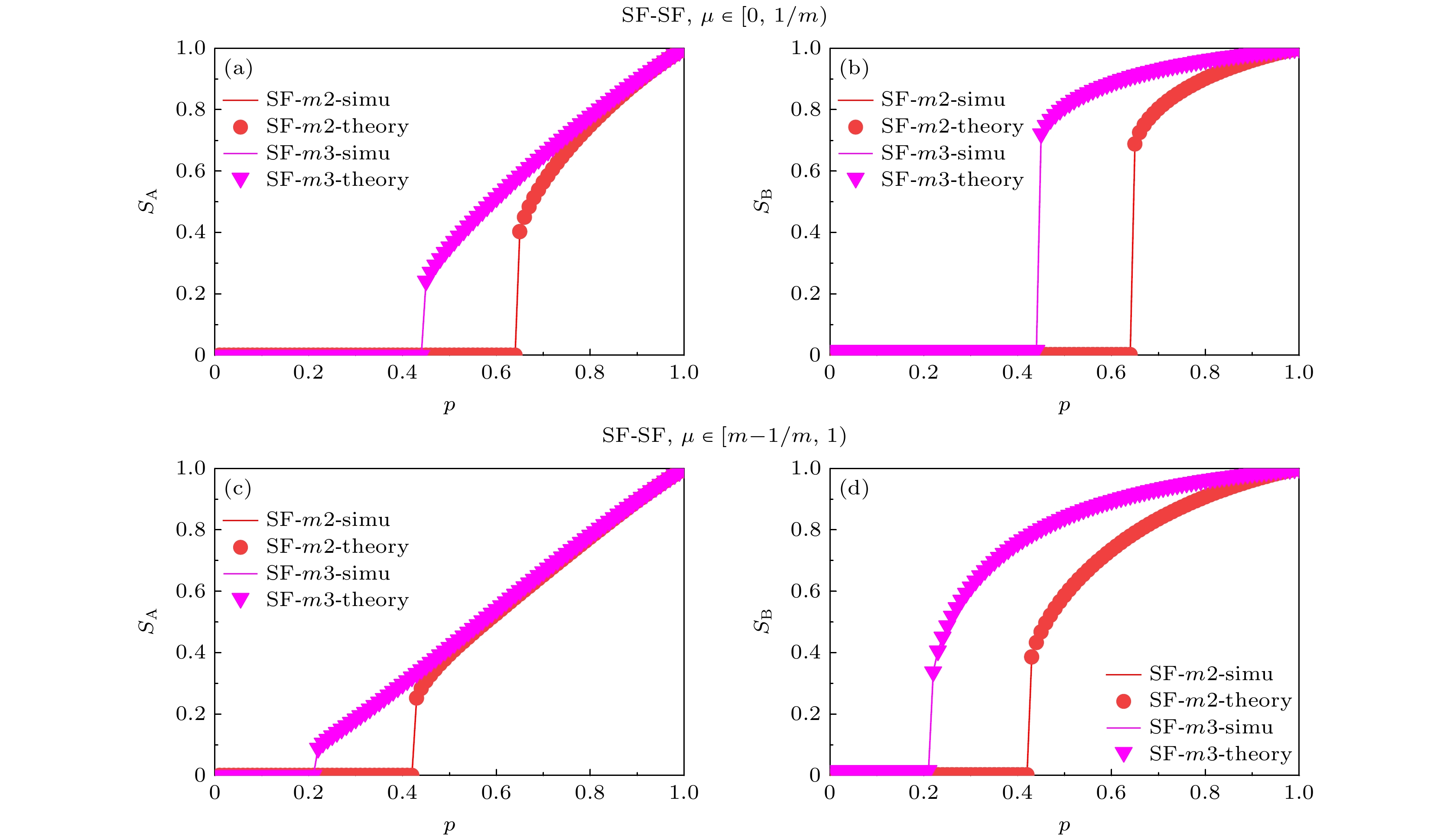
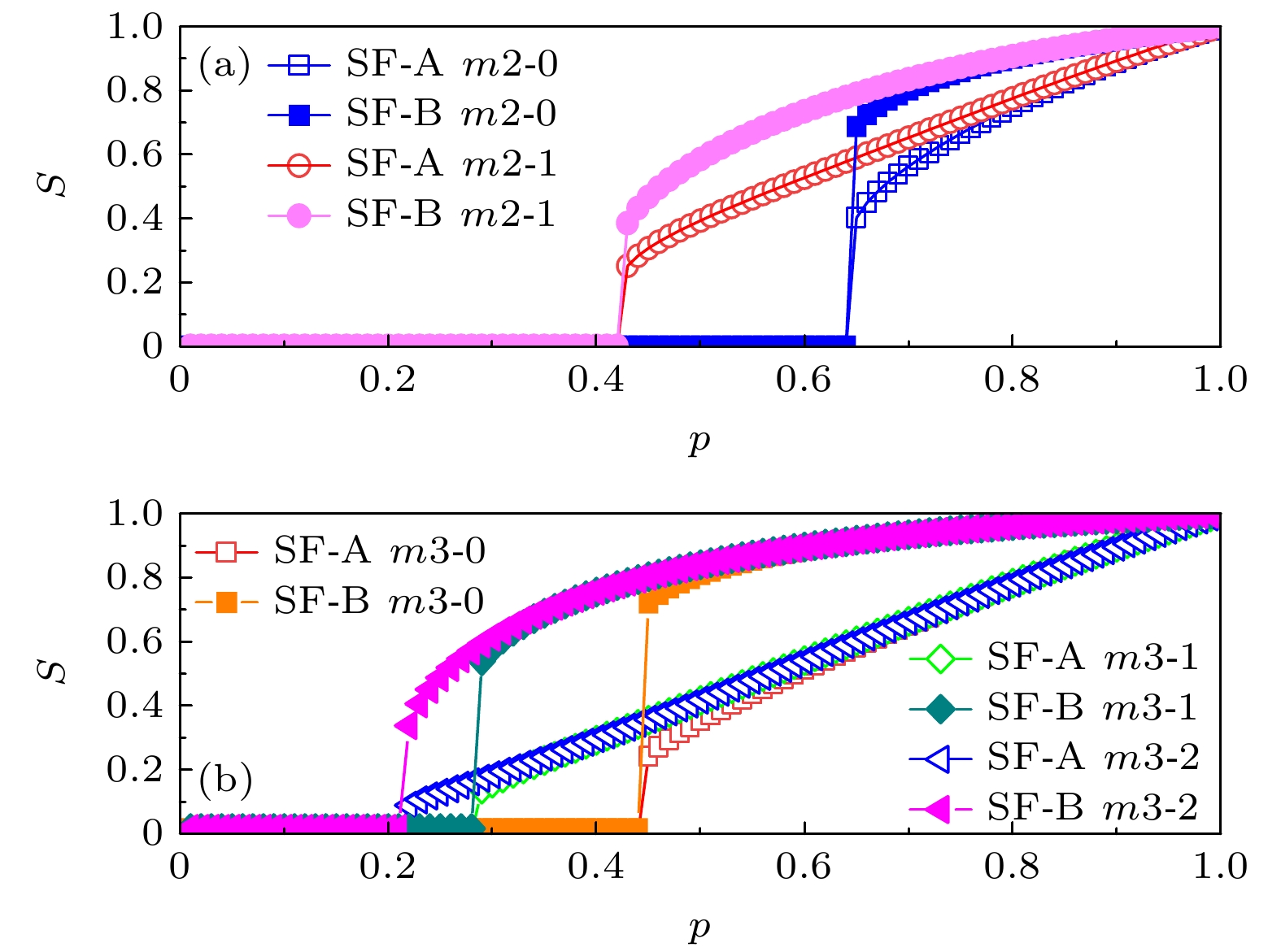
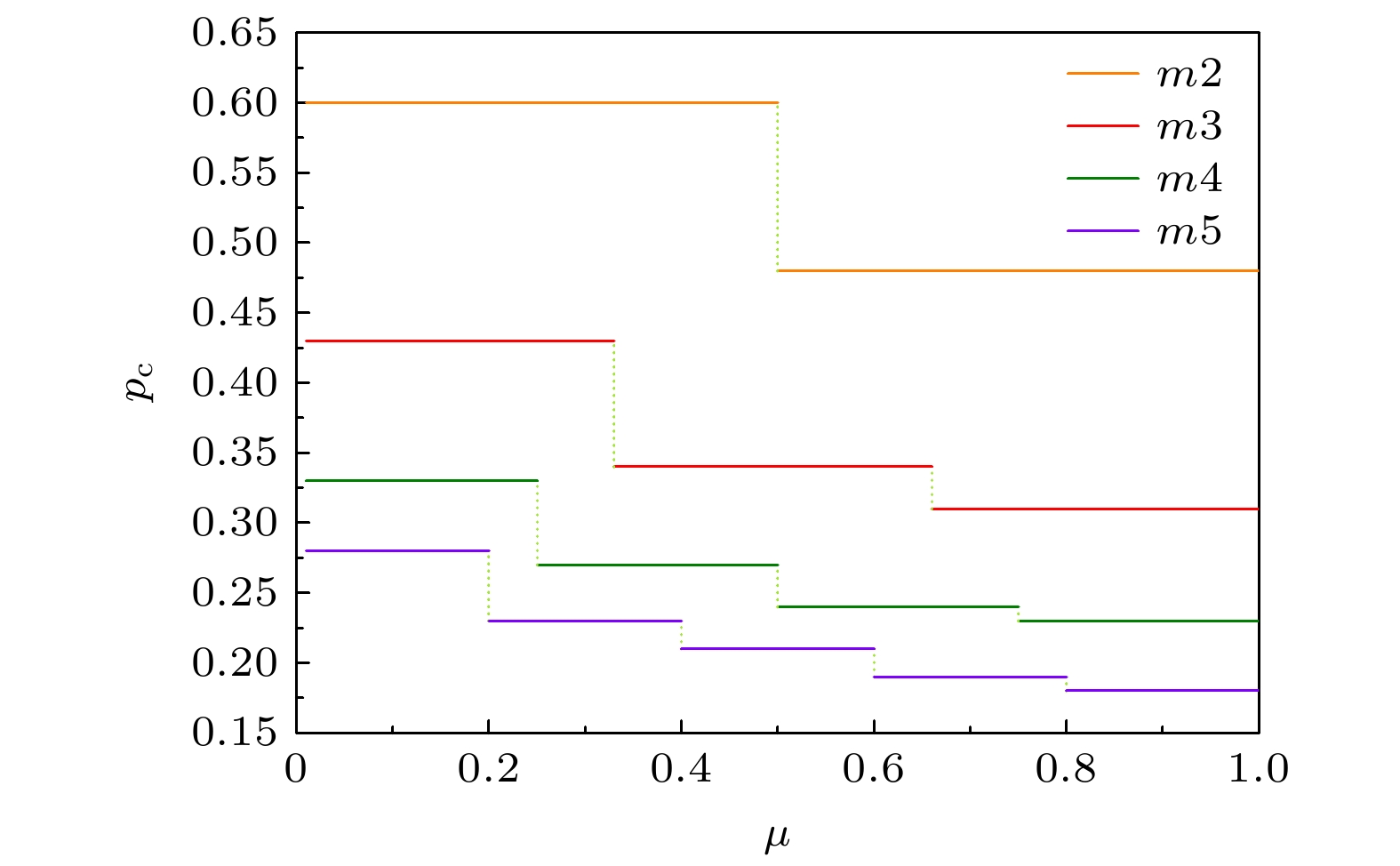
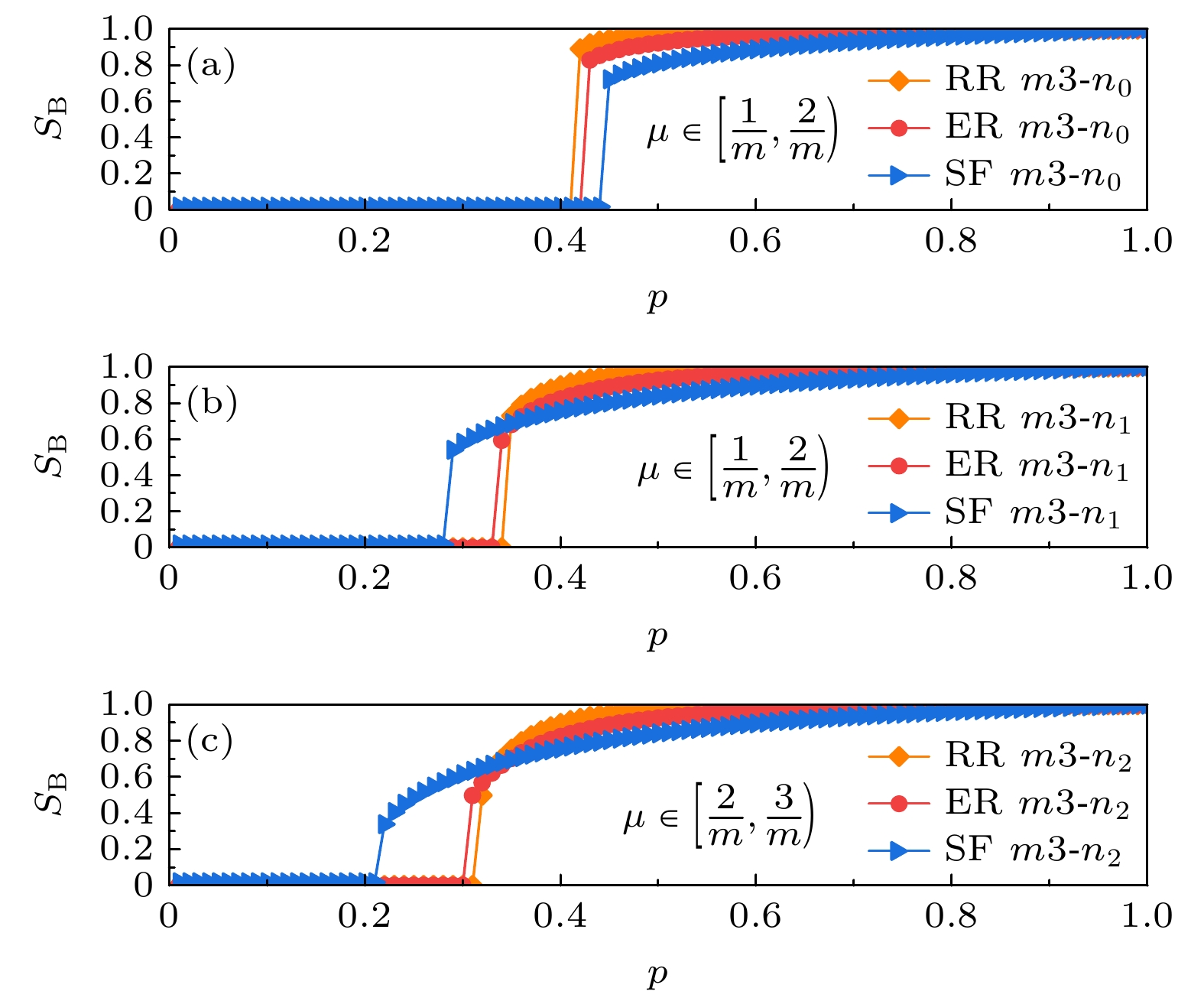
$\mu $ , is set for these edge-dependent clusters. When the failure rate of an edge-dependent cluster exceeds$\mu $ , the failure of the nodes in network A that depends on it, will happen. Based on the self-balancing probability method, a theoretical analysis framework is established. Through computer simulation verification of BINNEC under three classical network structures, the model's phase transition behavior and critical thresholds in the face of random attacks are analyzed. The results reveal that BINNEC under three network structures is as fragile as a single-element coupled network, exhibiting a first-order phase transition behavior. As the size of edge-dependent cluster$m$ increases, network robustness is enhanced. Moreover, with a constant size of edge-dependent cluster, a larger tolerance for node failure$\mu $ leads to stronger network robustness. Finally, this research reveals that under the same conditions of$m$ and$\mu $ , when the tolerance for node failure$\mu $ is insufficient to withstand the failure of a single edge, the degree distribution widens, and network robustness weakens. However, when the tolerance for node failure is sufficient to withstand the failure of at least one edge, the network robustness actually strengthens as the degree distribution increases. These findings provide a theoretical basis for studying such binary coupled models and also for guiding the secure design of real-world networks.-
Keywords:
- interdependent networks /
- binary coupling /
- failure tolerance /
- robustness
[1] Crucitti P, Latora V, Marchiori M 2004 Phys. Rev. E 69 045104
Google Scholar
[2] Mirzasoleiman B, Babaei M, Jalili M, Safari M 2011 Phys. Rev. E 84 046114
Google Scholar
[3] Wang J W, Rong L L, Zhang L, Zhang Z Z 2008 Physica A 387 6671
Google Scholar
[4] Panzieri S, Setola R 2008 Int. J. Model. Identif Control 3 69
Google Scholar
[5] Adenso-Díaz B, Mar-Ortiz J, Lozano S 2018 Int. J. Prod. Res. 56 5104
Google Scholar
[6] Yao H G, Xiao H H, Wei W 2022 Discret. Dyn. Nat. Soc. 23 49523
Google Scholar
[7] Rosato V, Issacharoff L, Tiriticco F, Meloni S, Porcellinins S D, Setola R 2008 Int. J. Crit. Infrastruct. 4 63
Google Scholar
[8] Buldyrev S V, Parshani R, Paul G, Stanley H E, Havlin S 2010 Nature 464 1025
Google Scholar
[9] Hu B, Li F, Zhou H S 2009 Chin. Phys. Lett. 26 128901
Google Scholar
[10] Mizutaka S, Yakubo K 2015 Phys. Rev. E 92 012814
Google Scholar
[11] Li J, Wu J, Li Y, Deng H Z, Tan Y J 2011 Chin. Phys. Lett. 28 058904
Google Scholar
[12] Parshani R, Buldyrev S V, Havlin S 2010 Phys. Rev. Lett. 105 048701
Google Scholar
[13] Dong G G, Gao J X, Tian L X, Du R J, He Y H 2012 Phys. Rev. E 85 016112
Google Scholar
[14] Gao J X, Buldyrev S V, Havlin S, Stanley E 2011 Phys. Rev. Lett. 107 195701
Google Scholar
[15] Jiang W, Liu R, Jia C 2020 Complexity 2020 3578736
Google Scholar
[16] Zhang H, Zhou J, Zou Y, Tan M, Xiao G X, Stanley H Z 2020 Phys. Rev. E 101 022314
Google Scholar
[17] Dong G, Chen Y, Wang F, Du R J, Tian L X, Stanley H E 2019 Chaos 29 073107
Google Scholar
[18] 韩伟涛, 伊鹏 2019 68 078902
Google Scholar
Han W T, Yi P 2019 Acta Phys. Sin. 68 078902
Google Scholar
[19] Wang Z X, Zhou D, Hu Y Q 2018 Phys. Rev. E 97 032306
Google Scholar
[20] Gao Y L, Chen S M, Zhou J, Stanley H E, Gao J 2021 Physica A 580 126136
Google Scholar
[21] Gao Y L, Yu H B, Zhou J, Zhou Y Z, Chen S M 2023 Chin. Phys. B 32 098902
Google Scholar
[22] Zhao Y Y, Zhou J, Zou Y, Guan S G, Gao Y L 2022 Chaos Solitons Fractals 156 111819
Google Scholar
[23] Xie Y F, Sun S W, Wang L, Xia C Y 2023 Phys. Lett. A 483 129063
Google Scholar
-
图 1 相依网络示意图
Figure 1. Schematic diagram of the interdependence network.
图 2 二元耦合网络模型及其级联失效示意图
Figure 2. Schematic diagram of binary coupled network model and cascade failure.
图 3 BINNEC中概率参数${L_{\text{A}}}$和${L_{\text{B}}}$的定义示意图
Figure 3. Schematic definition of probability parameters ${L_{\text{A}}}$ and ${L_{\text{B}}}$ in BINNEC.
图 4 RR BINNEC在极端$\mu $值和不同m 时, SA和SB与p的关系图
Figure 4. Plots of SA and SB versus p for the RR BINNEC at extreme $\mu $ values and at different m .
图 5 RR BINNEC在不同m 和$\mu $时SA和 SB 与p的关系对比图
Figure 5. Comparison chart of SA and SB versus p for the RR BINNEC at different $\mu $ and m.
图 6 ER BINNEC在极端$\mu $值和不同m时, SA和SB与p的关系图
Figure 6. Plots of SA and SB versus p for the ER BINNEC at extreme $\mu $ values and at different m.
图 7 ER BINNEC在不同m和$\mu $时SA和SB与p的关系对比图
Figure 7. Comparison chart of SA and SB versus p for the ER BINNEC at different $\mu $ and m.
图 8 SF BINNEC在极端$\mu $值和不同$m$时, SA和SB与p的关系图
Figure 8. Plots of SA and SB versus p for the SF BINNEC at extreme $\mu $ values and at different $m$.
图 9 SF BINNEC不同m和其对应不同$\mu $时, SA和SB与p的对比图
Figure 9. Comparison chart of SA and SB versus p for the SF BINNEC at different $\mu $ and m.
图 10 依赖群规模m取不同值时, ${p_{\text{c}}}$与$\mu $的关系图
Figure 10. Plot of ${p_{\text{c}}}$ versus $\mu $ for different dependency group sizes m.
图 11 不同失效边${n_i}$下SB与p的关系
Figure 11. Plot of SB versus p at different failure edges ${n_i}$.
-
[1] Crucitti P, Latora V, Marchiori M 2004 Phys. Rev. E 69 045104
Google Scholar
[2] Mirzasoleiman B, Babaei M, Jalili M, Safari M 2011 Phys. Rev. E 84 046114
Google Scholar
[3] Wang J W, Rong L L, Zhang L, Zhang Z Z 2008 Physica A 387 6671
Google Scholar
[4] Panzieri S, Setola R 2008 Int. J. Model. Identif Control 3 69
Google Scholar
[5] Adenso-Díaz B, Mar-Ortiz J, Lozano S 2018 Int. J. Prod. Res. 56 5104
Google Scholar
[6] Yao H G, Xiao H H, Wei W 2022 Discret. Dyn. Nat. Soc. 23 49523
Google Scholar
[7] Rosato V, Issacharoff L, Tiriticco F, Meloni S, Porcellinins S D, Setola R 2008 Int. J. Crit. Infrastruct. 4 63
Google Scholar
[8] Buldyrev S V, Parshani R, Paul G, Stanley H E, Havlin S 2010 Nature 464 1025
Google Scholar
[9] Hu B, Li F, Zhou H S 2009 Chin. Phys. Lett. 26 128901
Google Scholar
[10] Mizutaka S, Yakubo K 2015 Phys. Rev. E 92 012814
Google Scholar
[11] Li J, Wu J, Li Y, Deng H Z, Tan Y J 2011 Chin. Phys. Lett. 28 058904
Google Scholar
[12] Parshani R, Buldyrev S V, Havlin S 2010 Phys. Rev. Lett. 105 048701
Google Scholar
[13] Dong G G, Gao J X, Tian L X, Du R J, He Y H 2012 Phys. Rev. E 85 016112
Google Scholar
[14] Gao J X, Buldyrev S V, Havlin S, Stanley E 2011 Phys. Rev. Lett. 107 195701
Google Scholar
[15] Jiang W, Liu R, Jia C 2020 Complexity 2020 3578736
Google Scholar
[16] Zhang H, Zhou J, Zou Y, Tan M, Xiao G X, Stanley H Z 2020 Phys. Rev. E 101 022314
Google Scholar
[17] Dong G, Chen Y, Wang F, Du R J, Tian L X, Stanley H E 2019 Chaos 29 073107
Google Scholar
[18] 韩伟涛, 伊鹏 2019 68 078902
Google Scholar
Han W T, Yi P 2019 Acta Phys. Sin. 68 078902
Google Scholar
[19] Wang Z X, Zhou D, Hu Y Q 2018 Phys. Rev. E 97 032306
Google Scholar
[20] Gao Y L, Chen S M, Zhou J, Stanley H E, Gao J 2021 Physica A 580 126136
Google Scholar
[21] Gao Y L, Yu H B, Zhou J, Zhou Y Z, Chen S M 2023 Chin. Phys. B 32 098902
Google Scholar
[22] Zhao Y Y, Zhou J, Zou Y, Guan S G, Gao Y L 2022 Chaos Solitons Fractals 156 111819
Google Scholar
[23] Xie Y F, Sun S W, Wang L, Xia C Y 2023 Phys. Lett. A 483 129063
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4446
- PDF Downloads: 70
- Cited By: 0
