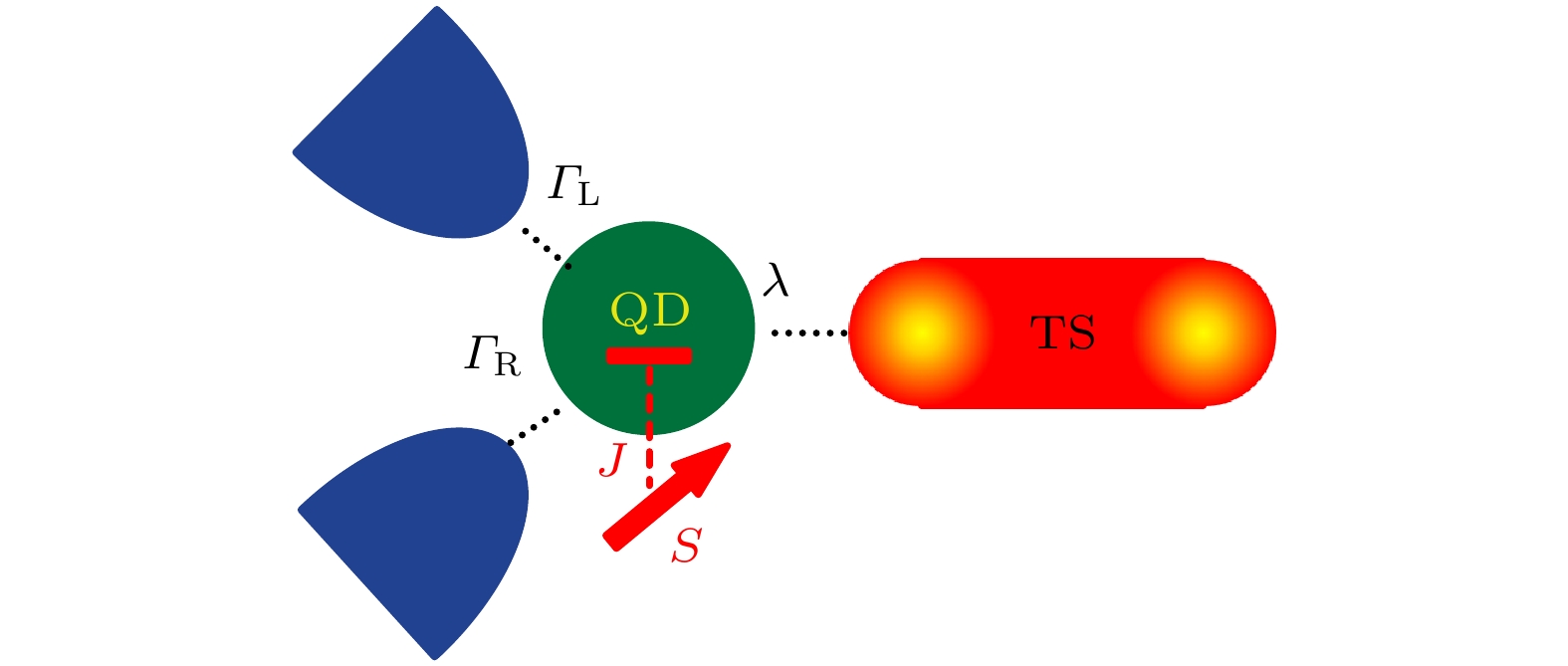
-
In quantum transport, especially in spintronics, its central theme is to manipulate spin degrees of freedom in solid-state systems, to understand the interaction between the particle spin and its solid-state environments and to make useful devices. Recently, Majorana fermion has been introduced into quantum transport and received much attention. In this paper, we study a thermal-driven transport model which consists of a quantum dot coupled with two normal metal leads, a impurity spin (whose angular quantum number is more than or equal to one-half) and a Majorana fermion. We focus on the interplay between Majorana fermion and the impurity in this exactly solvable model. It is found that the system can generate thermal-induced spin current, and the currents are affected by Majorana fermion and impurity. With large temperature difference, the currents are sensitive to gate voltage, and the quantitative relation between spin-up current and gate voltage tends to be linear when the coupling between Majorana and quantum dot is strong, showing Majorana fermion's robustness. In addition, the spin current induced by Majorana fermion exhibits an oscillating antisymmetric structure around zero-bias point. This spin current’s zero point is related to the angular quantum number of impurity spin. These results are expected to be useful in thermal-electric conversion devices, and may be observed in future experiments.
-
Keywords:
- spintronics /
- thermal-induced spin current /
- Majorana fermion /
- impurity spin
[1] Majorana E 1937 Nuovo Cimento 14 171
Google Scholar
[2] Nayak C, Simon S H, Stern A, Freedman M, Das Sarma S 2008 Rev. Mod. Phys. 80 1083
Google Scholar
[3] Stern A 2010 Nature 464 187
Google Scholar
[4] Chang C Z, Zhang J S, Feng X, et al. 2013 Science 340 167
Google Scholar
[5] He K, Wang Y, Xue Q K 2014 Nat. Sci. Rev. 1 38
Google Scholar
[6] 王力, 刘静思, 李吉, 周晓林, 陈向荣, 刘超飞, 刘伍明 2020 69 010303
Google Scholar
Wang L, Liu J S, Li J, Zhou X L, Chen X R, Liu C F, Liu W M 2020 Acta Phys. Sin. 69 010303
Google Scholar
[7] 李吉, 刘伍明 2018 67 110302
Google Scholar
Li J, Liu W M 2018 Acta Phys. Sin. 67 110302
Google Scholar
[8] 刘静思, 李吉, 刘伍明 2017 66 130305
Google Scholar
Liu J S, Li J, Liu W M 2017 Acta Phys. Sin. 66 130305
Google Scholar
[9] Chen Y H, Tao H S, Yao D X, Liu W M 2012 Phys. Rev. Lett. 108 246402
Google Scholar
[10] Jiang Z F, Li R D, Zhang S C, Liu W M 2005 Phys. Rev. B 72 045201
[11] Zhang X L, Liu L F, Liu W M 2005 Sci. Rep. 3 2908
[12] Reich E S 2012 Nature 483 132
Google Scholar
[13] Brouwer P W 2012 Science 336 989
Google Scholar
[14] Wilczek F 2012 Nature 486 195
Google Scholar
[15] Read N, Green D 2000 Phys. Rev. B 61 10267
Google Scholar
[16] Ivanov D A 2001 Phys. Rev. Lett. 86 268
Google Scholar
[17] Lutchyn R M, Sau J D, Das Sarma S 2010 Phys. Rev. Lett. 105 077001
Google Scholar
[18] Oreg Y, Refael G, von Oppen F 2010 Phys. Rev. Lett. 105 177002
Google Scholar
[19] Liu D E, Baranger H U 2011 Phys. Rev. B 84 201308(R
Google Scholar
[20] Napitu B D 2015 Eur. Phys. J. B 88 290
Google Scholar
[21] Lü H F, Lu H Z, Shen S Q 2014 Phys. Rev. B 90 195404
Google Scholar
[22] Liu D E, Cheng M, Lutchyn R M 2015 Phys. Rev. B 91 081405(R
Google Scholar
[23] Huo D M 2016 Eur. Phys. J. B 89 174
Google Scholar
[24] Niu P B, Liu L X, Su X Q, Dong L J, Shi Y L, Luo H G 2020 J. Magn. Magn. Mater. 506 166795
Google Scholar
[25] Bauer G E, MacDonald A H, Maekawa S 2010 Solid State Commun. 150 459
Google Scholar
[26] Bauer G E, Saitoh E, van Wees B J 2012 Nat. Mater. 11 391
Google Scholar
[27] Staring A A M, Molenkamp L W, Alphenaar B W, et al. 1993 Europhys. Lett. 22 57
Google Scholar
[28] Svensson S F, Hoffmann E A, Nakpathomkun N, et al. 2013 New J. Phys. 15 105011
Google Scholar
[29] Sanchez D, Lopez R 2013 Phys. Rev. Lett. 110 026804
Google Scholar
[30] Alidoust M, Halterman K, Valls O T 2015 Phys. Rev. B 92 014508
Google Scholar
[31] Niu P B, Liu L X, Su X Q, Dong L J, Shi Y L, Luo H G 2020 Physica E 124 114313
Google Scholar
[32] Niu P B, Wang Q, Nie Y H 2013 Chin. Phys. B 22 027307
Google Scholar
[33] Flensberg K 2010 Phys. Rev. B 82 180516(R
Google Scholar
[34] Kostyrko T, Bulka B R 2005 Phys. Rev. B 71 235306
Google Scholar
[35] Niu P B, Zhang Y Y, Wang Q, et al. 2012 Phys. Lett. A 376 1481
Google Scholar
[36] Meir Y, Wingreen N S 1992 Phys. Rev. Lett. 68 2512
Google Scholar
[37] Wang R Q, Sheng L, Shen R, Wang B, Xing D Y 2010 Phys. Rev. Lett. 105 057202
Google Scholar
[38] Luo H G, Ying Z J, Wang S J 1999 Phys. Rev. B 59 9710
Google Scholar
[39] Sun Q F, Guo H 2002 Phys. Rev. B 66 155308
Google Scholar
-
图 1 模型示意图. 系统由量子点(QD)、杂质大自旋(S)和拓扑超导线组成, 拓扑超导线的两端有两个马约拉纳费米子. 系统两端连接两个金属电极, 电极两端施加温度差
Figure 1. Model Diagram. The system consists of a quantum dot, a local large spin and a topological superconductor which supports Majorana fermions. There is a temperature gradient applied to the system.
图 2 S = 1/2时自旋向上电流(a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随温差的变化图
Figure 2. Spin-resolved currents (a), (b), spin current (c) and charge current (d) as a function of temperature difference for S = 1/2.
图 3 S = 1/2时自旋向上电流 (a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随门电压的变化图
Figure 3. Spin-resolved currents (a), (b), spin current (c) and charge current (d) as a function of gate voltage for S = 1/2.
图 4 S = 1时自旋向上电流(a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随门电压的变化图
Figure 4. Spin-resolved currents (a), (b), spin current (c) and charge current (d) as a function of gate voltage for S = 1.
-
[1] Majorana E 1937 Nuovo Cimento 14 171
Google Scholar
[2] Nayak C, Simon S H, Stern A, Freedman M, Das Sarma S 2008 Rev. Mod. Phys. 80 1083
Google Scholar
[3] Stern A 2010 Nature 464 187
Google Scholar
[4] Chang C Z, Zhang J S, Feng X, et al. 2013 Science 340 167
Google Scholar
[5] He K, Wang Y, Xue Q K 2014 Nat. Sci. Rev. 1 38
Google Scholar
[6] 王力, 刘静思, 李吉, 周晓林, 陈向荣, 刘超飞, 刘伍明 2020 69 010303
Google Scholar
Wang L, Liu J S, Li J, Zhou X L, Chen X R, Liu C F, Liu W M 2020 Acta Phys. Sin. 69 010303
Google Scholar
[7] 李吉, 刘伍明 2018 67 110302
Google Scholar
Li J, Liu W M 2018 Acta Phys. Sin. 67 110302
Google Scholar
[8] 刘静思, 李吉, 刘伍明 2017 66 130305
Google Scholar
Liu J S, Li J, Liu W M 2017 Acta Phys. Sin. 66 130305
Google Scholar
[9] Chen Y H, Tao H S, Yao D X, Liu W M 2012 Phys. Rev. Lett. 108 246402
Google Scholar
[10] Jiang Z F, Li R D, Zhang S C, Liu W M 2005 Phys. Rev. B 72 045201
[11] Zhang X L, Liu L F, Liu W M 2005 Sci. Rep. 3 2908
[12] Reich E S 2012 Nature 483 132
Google Scholar
[13] Brouwer P W 2012 Science 336 989
Google Scholar
[14] Wilczek F 2012 Nature 486 195
Google Scholar
[15] Read N, Green D 2000 Phys. Rev. B 61 10267
Google Scholar
[16] Ivanov D A 2001 Phys. Rev. Lett. 86 268
Google Scholar
[17] Lutchyn R M, Sau J D, Das Sarma S 2010 Phys. Rev. Lett. 105 077001
Google Scholar
[18] Oreg Y, Refael G, von Oppen F 2010 Phys. Rev. Lett. 105 177002
Google Scholar
[19] Liu D E, Baranger H U 2011 Phys. Rev. B 84 201308(R
Google Scholar
[20] Napitu B D 2015 Eur. Phys. J. B 88 290
Google Scholar
[21] Lü H F, Lu H Z, Shen S Q 2014 Phys. Rev. B 90 195404
Google Scholar
[22] Liu D E, Cheng M, Lutchyn R M 2015 Phys. Rev. B 91 081405(R
Google Scholar
[23] Huo D M 2016 Eur. Phys. J. B 89 174
Google Scholar
[24] Niu P B, Liu L X, Su X Q, Dong L J, Shi Y L, Luo H G 2020 J. Magn. Magn. Mater. 506 166795
Google Scholar
[25] Bauer G E, MacDonald A H, Maekawa S 2010 Solid State Commun. 150 459
Google Scholar
[26] Bauer G E, Saitoh E, van Wees B J 2012 Nat. Mater. 11 391
Google Scholar
[27] Staring A A M, Molenkamp L W, Alphenaar B W, et al. 1993 Europhys. Lett. 22 57
Google Scholar
[28] Svensson S F, Hoffmann E A, Nakpathomkun N, et al. 2013 New J. Phys. 15 105011
Google Scholar
[29] Sanchez D, Lopez R 2013 Phys. Rev. Lett. 110 026804
Google Scholar
[30] Alidoust M, Halterman K, Valls O T 2015 Phys. Rev. B 92 014508
Google Scholar
[31] Niu P B, Liu L X, Su X Q, Dong L J, Shi Y L, Luo H G 2020 Physica E 124 114313
Google Scholar
[32] Niu P B, Wang Q, Nie Y H 2013 Chin. Phys. B 22 027307
Google Scholar
[33] Flensberg K 2010 Phys. Rev. B 82 180516(R
Google Scholar
[34] Kostyrko T, Bulka B R 2005 Phys. Rev. B 71 235306
Google Scholar
[35] Niu P B, Zhang Y Y, Wang Q, et al. 2012 Phys. Lett. A 376 1481
Google Scholar
[36] Meir Y, Wingreen N S 1992 Phys. Rev. Lett. 68 2512
Google Scholar
[37] Wang R Q, Sheng L, Shen R, Wang B, Xing D Y 2010 Phys. Rev. Lett. 105 057202
Google Scholar
[38] Luo H G, Ying Z J, Wang S J 1999 Phys. Rev. B 59 9710
Google Scholar
[39] Sun Q F, Guo H 2002 Phys. Rev. B 66 155308
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4508
- PDF Downloads: 123
- Cited By: 0
