Phononic band structure and figure of merit of three-dimensional anisotropic asymmetric double-cone pentamode metamaterials

Cai Cheng-Xin; Chen Shao-Geng; Wang Xue-Mei; Liang Jun-Yan; Wang Zhao-Hong

doi:10.7498/aps.69.20200364

Abstract

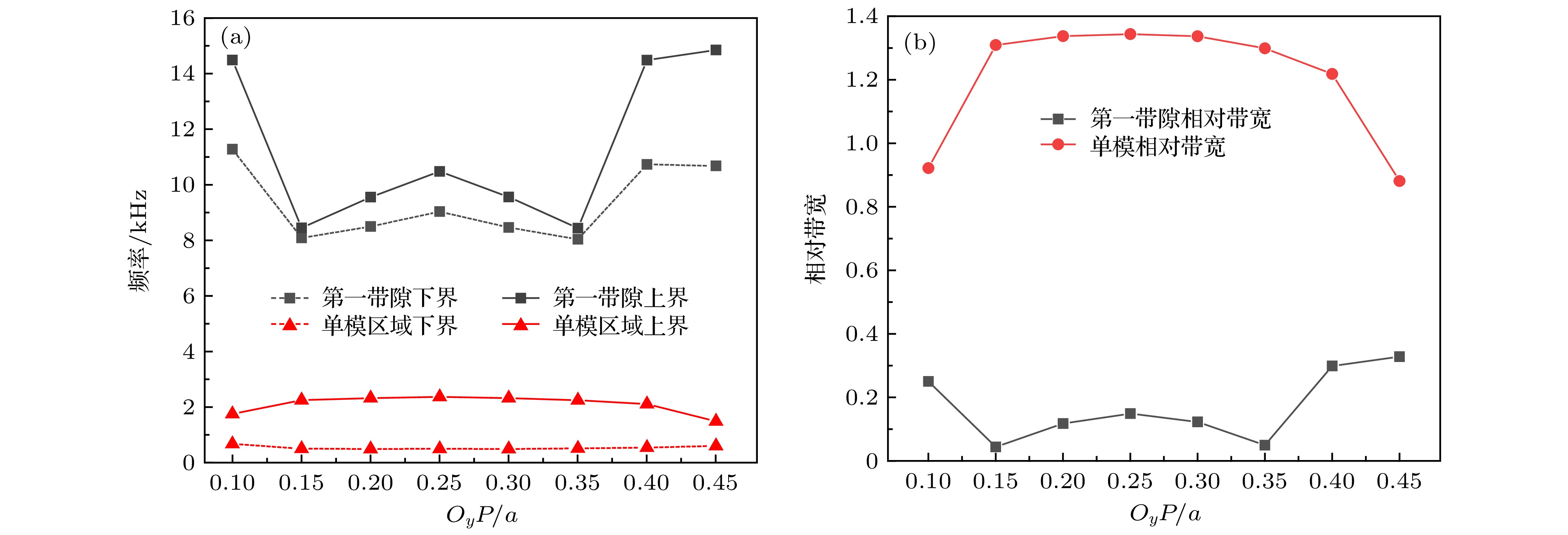
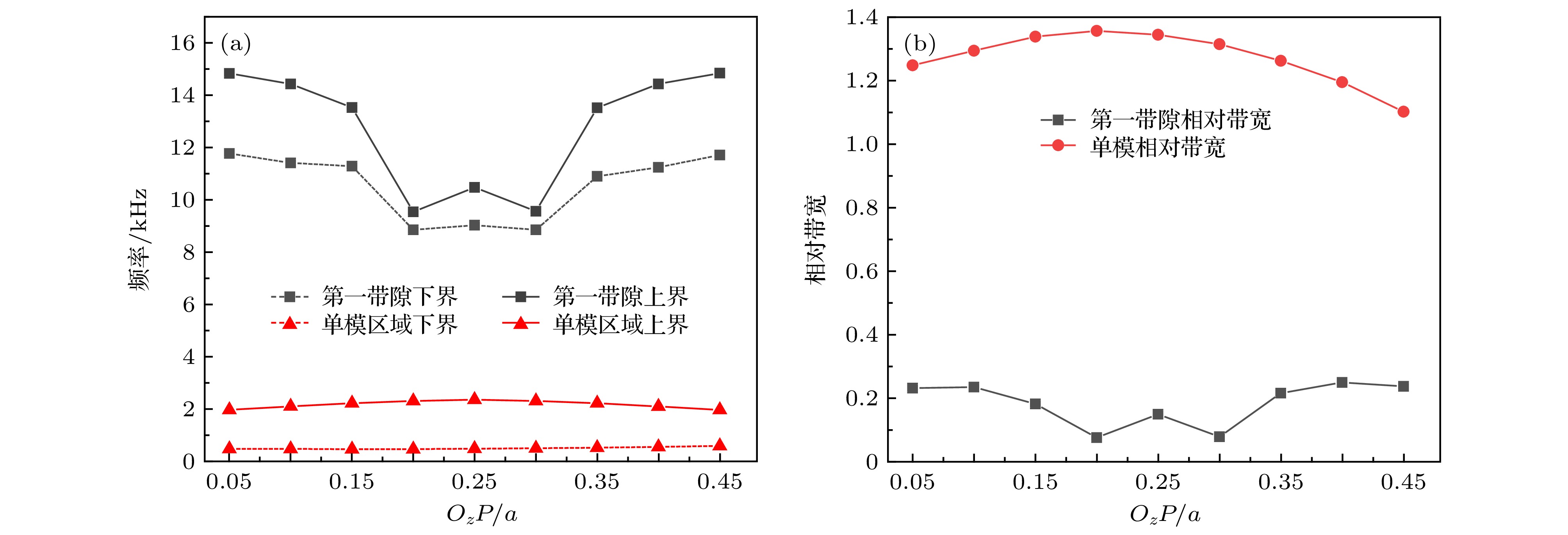
Pentamode metamaterial (PM) is a kind of artificial microstructure extremum material with solid morphology and fluid properties proposed by Milton and Cherkaey. By decoupling the compression and the shear waves, the periodic structure is difficult to be compressed, but the shear deformation occurs easily. Theoretically, acoustic metamaterials consisting of such periodic arrangement of structural units can achieve complete matching with water. Therefore, the characteristics of adjustable modulus anisotropy, small stuffing rate and broadband endow the PMs with excellent acoustic control ability, which has attracted more attention of researchers. In this paper, the narrow-diameter intersection point P (0.25a, 0.25a, 0.25a) of an isotropic three-dimensional PM selected as the reference point in four different directions (X-axis, Y-axis, Z-axis and body diagonal). When the P-point moves, the farther the P-point is, the greater the degree of anisotropy is. The introduction of anisotropy will cause the structural bifurcation of the three-dimensional PM to change structural parameters, and the structural parameters are important factors affecting the band characteristics of the three-dimensional PM of Bragg scattering. In order to study the influence of anisotropy on the band structure and pentamode properties of three-dimensional asymmetric double-cone PMs, we use the finite element simulation software COMSOL to calculate the primitive-cell of three-dimensional anisotropic PMs under Bloch boundary conditions. By adjusting the position of P point, four different types of three-dimensional anisotropic asymmetric double-cone PMs are constructed. Since the anisotropy changes in different directions have different effects on the parameters of the asymmetric double-cone structure, the band characteristics and the pentamode characteristics will also receive different degrees of influence. In this paper, the relationship between the degree of anisotropy and the band gap characteristics, single-mode region and figure of merit (FOM) are given, and the result can provide guidance for the design of asymmetric double-cone PM acoustic device. Compared with the isotropic double-cone PMs, the relative bandwidth of the first band gap of the anisotropic double-cone PMs can be broadened to 123%, and the FOM can be increased to 6.9 times. Due to the introduction of anisotropy, Due to the introduction of anisotropy, the structure of three-dimensional asymmetric double-cone PMs are more complex, the demand for sample fabrication is further improved, and the stability of PMs also reduced. Therefore, PMs with high stability and easy to be fabricated still needs further research and exploration.

Keywords:

Authors and contacts

1.
Key Laboratory of Grain Information Processing and Control (Henan University of Technology), Ministry of Education, Zhengzhou 450001, China
2.
Henan Provincial Key Laboratory of Grain Photoelectric Detection and Control, Henan University of Technology, Zhengzhou 450001, China
3.
College of Information Science and Engineering, Henan University of Technology, Zhengzhou 450001, China
4.
School of Electronic and Information Engineering, Key Laboratory for Physical Electronics and Devices of the Ministry of Education, Xi’an Jiaotong University, Xi’an 710049, China

Corresponding author: Cai Cheng-Xin, cxcai2018@haut.edu.cn

FullText HTML

References

[1]	Milton G W, Cherkaev A V 1995 J. Eng. Mater. Technol. 117 483 Google Scholar
[2]	Kadic M, Bückmann T, Stenger N, Thiel M, Wegener M 2012 Appl. Phys. Lett. 100 191901 Google Scholar
[3]	陈毅, 刘晓宁, 向平, 胡更开 2016 力学进展 46 201609 Google Scholar Chen Y, Liu X N, Xiang P, Hu G K 2016 Adv. Mech. 46 201609 Google Scholar
[4]	王兆宏, 蔡成欣, 楚杨阳, 刘广顺 2017 光电工程 44 34 Google Scholar Wang Z H, Cai C X, Chu Y Y, Liu G S 2017 Opto-Electron. Eng. 44 34 Google Scholar
[5]	Milton G W, Briane M, Wills J R 2006 New J. Phys. 8 248 Google Scholar
[6]	Norris A N 2008 Proc. R. Soc. A 464 2411 Google Scholar
[7]	Scandrett L C, Boisvert J E, Howarth T R 2010 J. Acoust. Soc. Am. 127 2856 Google Scholar
[8]	Scandrett L C, Boisvert J E, Howarth T R 2011 Wave Motion 48 505 Google Scholar
[9]	Boisvert J E, Scandrett L C, Howarth T R 2016 J. Acoust. Soc. Am. 139 3404 Google Scholar
[10]	Schittny R, Bückmann T, Kadic M, Wegener M 2013 Appl. Phys. Lett. 103 231905 Google Scholar
[11]	Gokhale N H, Cipolla J L, Norris A N 2012 J. Acoust. Soc. Am. 132 4
[12]	Kadic M, Buckmann T, Schittny R, Gumbsch P, Wegener M 2014 Phys. Rev. Appl. 2 054007 Google Scholar
[13]	Cai C X, Wang Z H, Li Q W, Xu Z, Tian X G 2015 J. Phys. D: Appl. Phys. 48 175103 Google Scholar
[14]	Huang Y, Lu X G, Liang G Y, Xu Z 2016 Phys. Lett. A 380 1334 Google Scholar
[15]	Wang G, Jin L, Zhang L, Xu Z 2017 AIP Adv. 7 025309 Google Scholar
[16]	Tian Y, Wei Q, Cheng Y, Xu Z, Liu X J 2015 Appl. Phys. Lett. 107 221906 Google Scholar
[17]	Sun Z Y, Jia H, Chen Y, Wang Z, Yang J 2018 J. Acoust. Soc. Am. 143 1029 Google Scholar
[18]	Chen Y, Liu X N, Hu G K 2015 Sci. Rep. 5 15745 Google Scholar
[19]	Chen J G, Liu J H, Liu X Z 2018 AIP Adv. 8 085024 Google Scholar
[20]	张向东, 陈虹, 王磊, 赵志高, 赵爱国 2015 64 134303 Google Scholar Zhang X D, Chen H, Wang L, Zhao Z G, Zhao A G 2015 Acta Phys. Sin. 64 134303 Google Scholar
[21]	陆智淼, 蔡力, 温激鸿, 温熙森 2016 65 174301 Google Scholar Lu Z M, Cai L, Wen J H, Wen X S 2016 Acta Phys. Sin. 65 174301 Google Scholar
[22]	Chen H Y, Chan C T 2007 Appl. Phys. Lett. 91 183518 Google Scholar
[23]	Chen H Y, Chan C T 2010 J. Phys. D: Appl. Phys. 43 113001 Google Scholar
[24]	Cai C X, Han C, Wu J F, Wang Z H, Zhang Q H 2019 J. Phys. D: Appl. Phys. 52 045601 Google Scholar
[25]	Wang Z H, Cai C X, Li Q W, Li J, Xu Z 2016 J. Appl. Phys. 120 024903 Google Scholar
[26]	Bückmann T, Schittny R, Thiel M, Kadic M, Milton G W, Wegener M 2014 New J. Phys. 16 033032 Google Scholar

Cited By

图 1 (a)各向同性五模超材料晶胞与(b)−(e)各向异性五模超材料晶胞结构示意图

Figure 1. The unit cell structure of isotropy (a) and (b)−(e) anisotropic pentamode materials.

DownLoad: Full-Size Img PowerPoint

图 2 P点沿空间对角线方向偏移0.25倍对角线长度时的能带结构

Figure 2. The band structure of pentamode material with ${O_{\rm{s}}}P/\sqrt 3 a = 0.25$.

DownLoad: Full-Size Img PowerPoint

图 3 模型1的第一带隙与单模区域的(a)上下界频率; (b)相对带宽

Figure 3. (a) The upper and lower edges and (b) relative bandwidth of the first phononic band gaps and single mode area of model 1.

DownLoad: Full-Size Img PowerPoint

图 7 各向异性对非对称双锥五模超材料品质因数的影响

Figure 7. The influence of anisotropy on the figure of merit of asymmetric double-cone pentamode materials.

DownLoad: Full-Size Img PowerPoint

图 4 模型2的第一带隙与单模区域的(a)上下界频率; (b)相对带宽

Figure 4. (a) The upper and lower edges and (b) relative bandwidth of the first phononic band gaps and single mode area of model 2.

DownLoad: Full-Size Img PowerPoint

图 5 模型3的第一带隙与单模区域的(a)上下界频率; (b)相对带宽

Figure 5. (a) The upper and lower edges and (b) relative bandwidth of the first phononic band gaps and single mode area of model 3.

DownLoad: Full-Size Img PowerPoint

图 6 模型4的第一带隙与单模区域的(a)上下界频率; (b)相对带宽

Figure 6. (a) The upper and lower edges and (b) relative bandwidth of the first phononic band gaps and single mode area of model 4.

DownLoad: Full-Size Img PowerPoint

map

[1]	Milton G W, Cherkaev A V 1995 J. Eng. Mater. Technol. 117 483 Google Scholar
[2]	Kadic M, Bückmann T, Stenger N, Thiel M, Wegener M 2012 Appl. Phys. Lett. 100 191901 Google Scholar
[3]	陈毅, 刘晓宁, 向平, 胡更开 2016 力学进展 46 201609 Google Scholar Chen Y, Liu X N, Xiang P, Hu G K 2016 Adv. Mech. 46 201609 Google Scholar
[4]	王兆宏, 蔡成欣, 楚杨阳, 刘广顺 2017 光电工程 44 34 Google Scholar Wang Z H, Cai C X, Chu Y Y, Liu G S 2017 Opto-Electron. Eng. 44 34 Google Scholar
[5]	Milton G W, Briane M, Wills J R 2006 New J. Phys. 8 248 Google Scholar
[6]	Norris A N 2008 Proc. R. Soc. A 464 2411 Google Scholar
[7]	Scandrett L C, Boisvert J E, Howarth T R 2010 J. Acoust. Soc. Am. 127 2856 Google Scholar
[8]	Scandrett L C, Boisvert J E, Howarth T R 2011 Wave Motion 48 505 Google Scholar
[9]	Boisvert J E, Scandrett L C, Howarth T R 2016 J. Acoust. Soc. Am. 139 3404 Google Scholar
[10]	Schittny R, Bückmann T, Kadic M, Wegener M 2013 Appl. Phys. Lett. 103 231905 Google Scholar
[11]	Gokhale N H, Cipolla J L, Norris A N 2012 J. Acoust. Soc. Am. 132 4
[12]	Kadic M, Buckmann T, Schittny R, Gumbsch P, Wegener M 2014 Phys. Rev. Appl. 2 054007 Google Scholar
[13]	Cai C X, Wang Z H, Li Q W, Xu Z, Tian X G 2015 J. Phys. D: Appl. Phys. 48 175103 Google Scholar
[14]	Huang Y, Lu X G, Liang G Y, Xu Z 2016 Phys. Lett. A 380 1334 Google Scholar
[15]	Wang G, Jin L, Zhang L, Xu Z 2017 AIP Adv. 7 025309 Google Scholar
[16]	Tian Y, Wei Q, Cheng Y, Xu Z, Liu X J 2015 Appl. Phys. Lett. 107 221906 Google Scholar
[17]	Sun Z Y, Jia H, Chen Y, Wang Z, Yang J 2018 J. Acoust. Soc. Am. 143 1029 Google Scholar
[18]	Chen Y, Liu X N, Hu G K 2015 Sci. Rep. 5 15745 Google Scholar
[19]	Chen J G, Liu J H, Liu X Z 2018 AIP Adv. 8 085024 Google Scholar
[20]	张向东, 陈虹, 王磊, 赵志高, 赵爱国 2015 64 134303 Google Scholar Zhang X D, Chen H, Wang L, Zhao Z G, Zhao A G 2015 Acta Phys. Sin. 64 134303 Google Scholar
[21]	陆智淼, 蔡力, 温激鸿, 温熙森 2016 65 174301 Google Scholar Lu Z M, Cai L, Wen J H, Wen X S 2016 Acta Phys. Sin. 65 174301 Google Scholar
[22]	Chen H Y, Chan C T 2007 Appl. Phys. Lett. 91 183518 Google Scholar
[23]	Chen H Y, Chan C T 2010 J. Phys. D: Appl. Phys. 43 113001 Google Scholar
[24]	Cai C X, Han C, Wu J F, Wang Z H, Zhang Q H 2019 J. Phys. D: Appl. Phys. 52 045601 Google Scholar
[25]	Wang Z H, Cai C X, Li Q W, Li J, Xu Z 2016 J. Appl. Phys. 120 024903 Google Scholar
[26]	Bückmann T, Schittny R, Thiel M, Kadic M, Milton G W, Wegener M 2014 New J. Phys. 16 033032 Google Scholar

Catalog

Vol. 69, Issue 13 - 2020-07-05

Metrics

Abstract views: 12044
PDF Downloads: 198
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板