-
Interfacial mechanical properties have a great influence on the overall mechanical performance of graphene/flexible substrate composite structure. Therefore, it is necessary to study interfacial shear stress transfer between graphene and flexible substrate. In this paper, a two-dimensional nonlinear shear-lag model (2D model) is presented. Taking the effects of Poisson’s ratio of the graphene and substrate into consideration, the bidirectional interfacial shear stress transfer between graphene and flexible substrate subjected to uniaxial tension is investigated by the 2D model when the Poisson’s ratio of substrate is larger than that of graphene. In the elastic bonding stage, the semi-analytical solutions of the bidirectional normal strains of the graphene and bidirectional interfacial shear stresses are derived, respectively, and their distributions at different positions are illustrated. The critical strain for interfacial sliding is derived by the 2D model, and the results show that the critical strain has a micron-scaled characteristic width. The width size of graphene has a significant influence on the critical strain when it is less than the characteristic width, but the size effect can be ignored when the width of graphene is larger than the characteristic width. In addition, the Poisson’s ratio of substrate can also affect the critical strain. Based on the 2D model, the finite element simulations are made to investigate the distribution of graphene's normal strains and interfacial shear stresses in the interfacial sliding stage. Furthermore, compared with the results obtained via one-dimensional nonlinear shear-lag model (1D model), the distributions of graphene’s normal strains and interfacial shear stresses calculated by 2D model show obvious bidimensional effects both in the elastic bonding stage and in the interfacial sliding stage when the width of graphene is large. There exists a compression strain in the graphene and a transverse (perpendicular to the tensile direction) shear stress in the interface, which are neglected in the 1D model. And the distributions of graphene’s tensile strain and longitudinal (along the tensile direction) interfacial shear stress are not uniform along the width, which are also significantly different from the results of 1D model. Moreover, the critical strain for interfacial sliding derived by the 2D model is lower than that obtained by the 1D model. However, when the width of graphene is small enough, the 2D model can be approximately replaced by the 1D model. Finally, by fitting the Raman experimental results, the reliability of the 2D model is verified, and the interfacial stiffness (100 TPa/m) and shear strength (0.295 MPa) between graphene and polyethylene terephthalate (PET) substrate are calculated.
-
Keywords:
- graphene/flexible substrate structure /
- Poisson’s ratio /
- interfacial shear stress transfer /
- two-dimensional nonlinear shear-lag model
[1] Geim A K 2009 Science 324 1530
Google Scholar
[2] Bolotin K I, Sikes K J, Jiang Z, Klima M, Fudenberg G, Hone J, Kim P, Stormer H L 2008 Solid State Commun. 146 351
Google Scholar
[3] Lee C G, Wei X D, Kysar J W, Hone J 2008 Science 321 385
Google Scholar
[4] Li X, Zhang R J, Yu W J, Wang K L, Wei J Q, Wu D H, Cao A Y, Li Z H, Cheng Y, Zheng Q S, Ruoff R S, Zhu H W 2012 Sci. Rep. 2 870
Google Scholar
[5] Young R J, Kinloch I A, Gong L, Novoselov K S 2012 Compos. Sci. Technol. 72 1459
Google Scholar
[6] Gong L, Kinloch I A, Young R J, Riaz I, Jalil R, Novoselov K S 2010 Adv. Mater. 22 2694
Google Scholar
[7] Jiang T, Huang R, Zhu Y 2014 Adv. Funct. Mater. 24 396
Google Scholar
[8] Xu C C, Xue T, Guo J G, Qin Q H, Wu S, Song H B, Xie H M 2015 J. Appl. Phys. 117 164301
Google Scholar
[9] Xu C C, Xue T, Guo J G, Kang Y L, Qiu W, Song H B, Xie H M 2015 Mater. Lett. 161 755
Google Scholar
[10] 仇巍, 张启鹏, 李秋, 许超宸, 郭建刚 2017 66 166801
Google Scholar
Qiu W, Zhang Q P, Li Q, Xu C C, Guo J G 2017 Acta Phys. Sin. 66 166801
Google Scholar
[11] Cox H L 1952 Br. J. Appl. Phys. 3 72
Google Scholar
[12] Guo G D, Zhu Y 2015 J. Appl. Mech. 82 031005
Google Scholar
[13] Cui Z, Guo J G 2016 AIP Adv. 6 125110
Google Scholar
[14] Zhang S L, Li J C M 2004 J. Polym. Sci., Part B: Polym. Phys. 42 260
Google Scholar
[15] Kurennov S S 2014 Mech. Compos. Mater. 50 105
Google Scholar
[16] Mathias J D, Grédiac M, Balandraud X 2006 Int. J. Solids Struct. 43 6921
Google Scholar
[17] Randrianalisoa J, Dendievel R, Bréchet Y 2011 Compos. Part B: Eng. 42 2055
Google Scholar
[18] Park K, Paulino G H 2011 Appl. Mech. Rev. 64 060802
Google Scholar
[19] Dourado N, Silva F G A, de Moura M F S F 2018 Constr. Build. Mater. 176 14
Google Scholar
[20] Högberg J L 2006 Int. J. Fract. 141 549
Google Scholar
[21] Camanho P P, Davila C G, de Moura M F 2003 J. Compos. Mater. 37 1415
Google Scholar
[22] Faccio R, Denis P A, Pardo H, Goyenola C, Mombrú A W 2009 J. Phys. Condens. Matter 21 285304
Google Scholar
[23] 许超宸 2019 博士学位论文 (天津: 天津大学)
Xu C C 2019 Ph. D. Dissertation (Tianjin: Tianjin University) (in Chinese)
[24] Mohiuddin T M G, Lombardo A, Nair R R, Bonetti A, Savini G, Jalil R, Bonini N, Basko D M, Galiotis C, Marzari N, Novoselov K S, Geim A K, Ferrari A C 2009 Phys. Rev. B 79 205433
Google Scholar
[25] Sakata H, Dresselhaus G, Dresselhaus M S, Endo M 1988 J. Appl. Phys. 63 2769
Google Scholar
[26] Ni Z H, Yu T, Lu Y H, Wang Y Y, Feng Y P, Shen Z X 2008 ACS Nano 2 2301
Google Scholar
[27] Yu T, Ni Z H, Du C L, You Y M, Wang Y Y, Shen Z X 2008 J. Phys. Chem. C 112 12602
[28] Koukaras E N, Androulidakis C, Anagnostopoulos G, Papagelis K, Galiotis C 2016 Extreme Mech. Lett. 8 191
Google Scholar
-
图 1 受单轴拉伸载荷的石墨烯/基底结构示意图
Figure 1. Schematic diagram of the graphene/substrate structure under uniaxial tension.
图 2 石墨烯单元的应力状态示意图
Figure 2. The force balance of an element of graphene.
图 3 局部界面上一点的切应力分析
Figure 3. Analysis of interfacial shear stresses at local interface.
图 4 (a) 二维非线性剪滞模型; (b) 双线性内聚力模型(Ⅱ + Ⅲ型混合模式)
Figure 4. (a) Two-dimensional nonlinear shear-lag model; (b) bilinear cohesive shear-mode (Ⅱ + Ⅲ) law.
图 5 弹性粘结阶段 (εsx = 0.2%) 时石墨烯正应变 (a) εx和(b) εy以及界面切应力 (c) τzx和(d) τzy的分布
Figure 5. Distributions of graphene’s normal strains (a) εx and (b) εy; distributions of interfacial shear stresses (c) τzx and (d) τzy at the elastic bonding stage (εsx = 0.2%).
图 6 典型线处石墨烯正应变 (a) εx和(b) εy以及界面切应力 (c) τzx和(d) τzy的分布
Figure 6. Distributions of graphene’s strains (a) εx and (b) εy; distributions of interfacial shear stresses (c) τzx and (d) τzy along several representative lines.
图 7 不同基底泊松比情况下滑移临界应变εsxc随石墨烯宽度W的变化(线为理论值, 散点为有限元值)
Figure 7. Variation of the critical strain for sliding with the width of graphene at different Poisson's ratio of substrate (the lines are the theoretical results, and the scatter points are the FEM results).
图 8 界面滑移阶段示意图
Figure 8. Schematic diagram of interfacial sliding stage.
图 9 界面滑移阶段 (εsx = 1%) 时石墨烯正应变 (a) εx和(b) εy以及界面切应力 (c) τzx和(d) τzy.的分布
Figure 9. Distributions of graphene’s normal strains (a) εx and (b) εy; distributions of interfacial shear stresses (c) τzx and (d) τzy at the interfacial sliding stage (εsx = 1%).
图 10 不同基底应变下石墨烯中心C点处压缩应变εyC随石墨烯宽度的变化
Figure 10. Variation of compressive strain εyC at the center point C of graphene with its width when the strain of substrate is different.
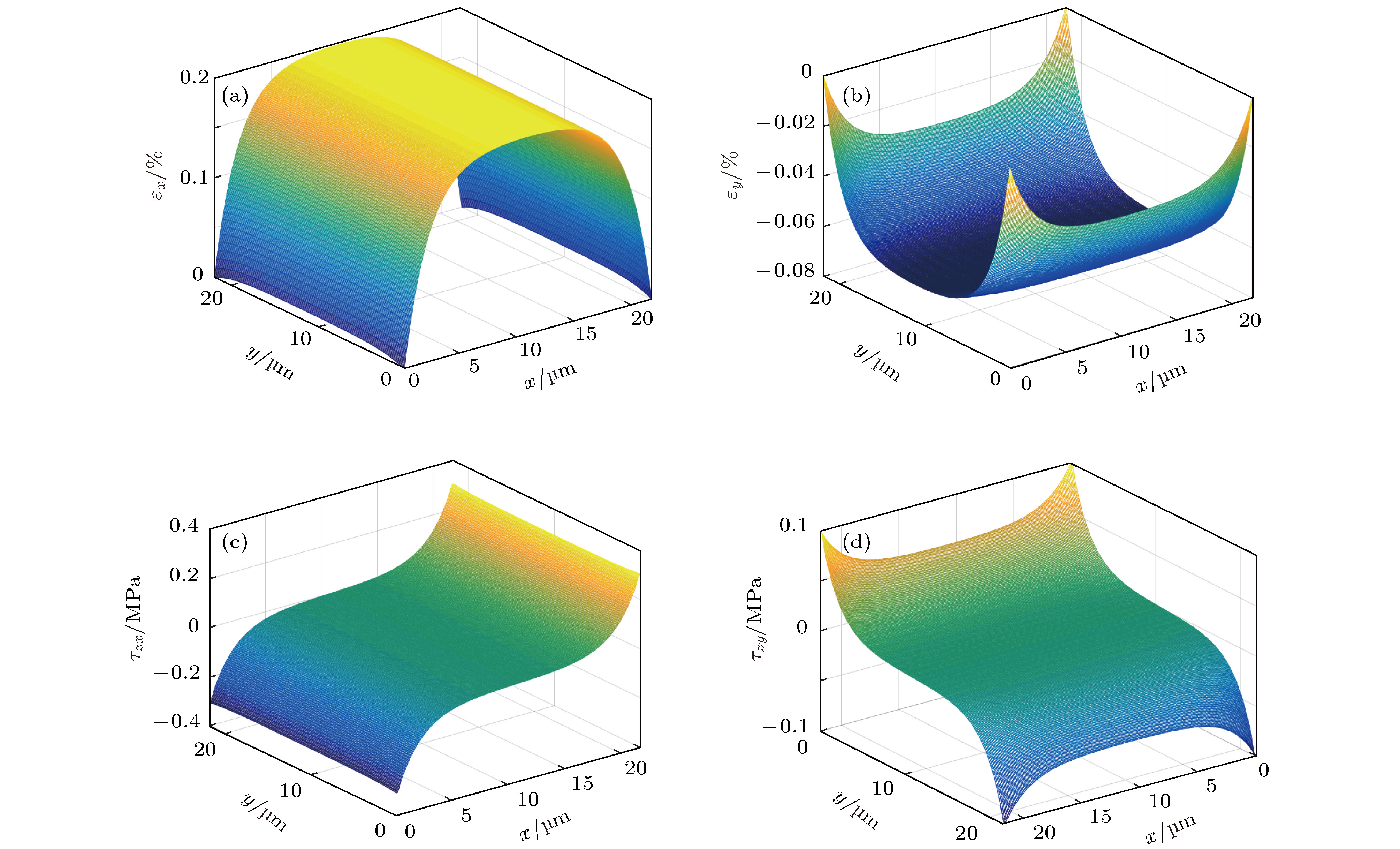
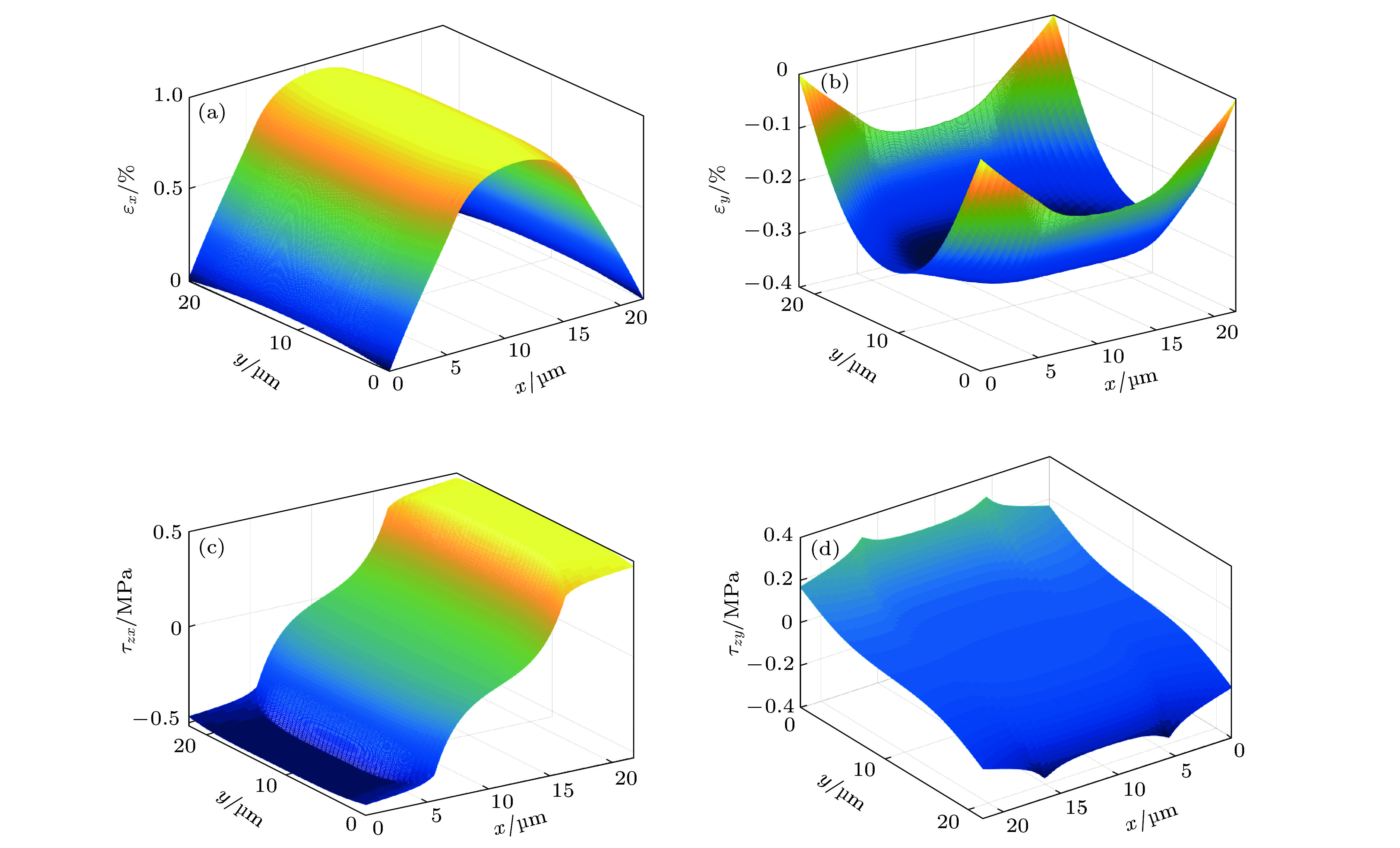
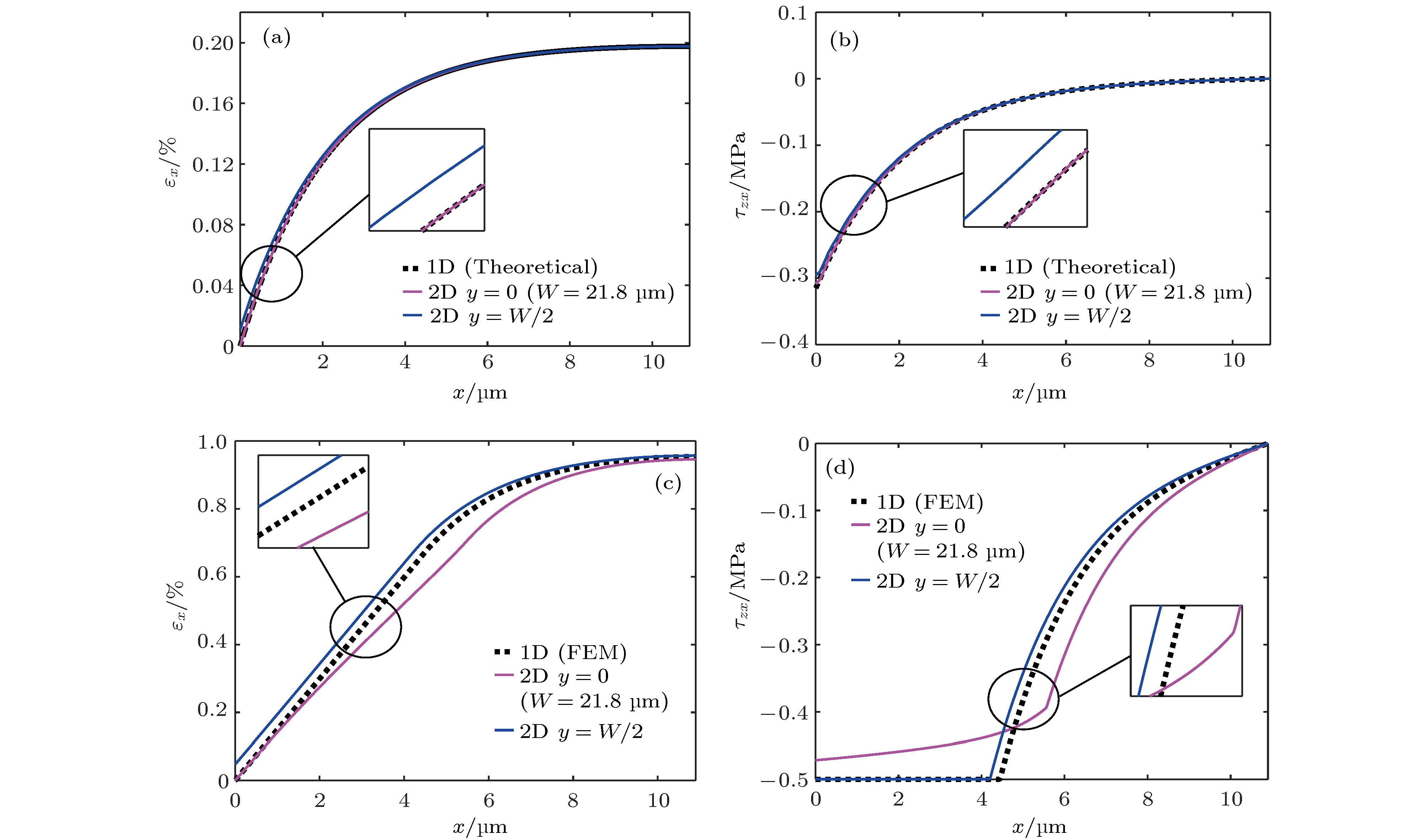
图 11 二维模型与一维模型结果的比较 (W = 21.8 μm) (a) εx和(b) τzx在弹性粘结阶段(εsx = 0.2%); (c) εx和(d) τzx在界面滑移阶段 (εsx = 1%)
Figure 11. Comparisons of the results obtained via one-dimensional and two-dimensional models (W = 21.8 μm): (a) εx and (b) τzx at the elastic bonding stage (εsx = 0.2%); (c) εx and (d) τzx at the interfacial sliding stage (εsx = 1%).
图 12 二维模型与一维模型计算结果的比较 (W = 1 μm) (a) εx和(b) τzx在界面滑移阶段 (εsx = 1%)
Figure 12. Comparisons of the results obtained via one-dimensional and two-dimensional models (W = 1 μm): (a) εx and (b) τzx at the interfacial sliding stage (εsx = 1%).
图 13 利用二维模型与实验数据拟合 (a) 基底拉伸应变εsx = 0.25%时εm沿石墨烯中心线(y = W/2)的分布; (b) 不同基底载荷作用下石墨烯中心C点处
$ \varepsilon_{\rm m}^{C} $ 的大小Figure 13. Fitting results of experimental data by using 2D model: (a) εm along the centerline (y = W/2) when the tensile strain εsx = 0.25%; (b)
$ \varepsilon_{\rm m}^{C} $ at the center point C under different tensile loads. -
[1] Geim A K 2009 Science 324 1530
Google Scholar
[2] Bolotin K I, Sikes K J, Jiang Z, Klima M, Fudenberg G, Hone J, Kim P, Stormer H L 2008 Solid State Commun. 146 351
Google Scholar
[3] Lee C G, Wei X D, Kysar J W, Hone J 2008 Science 321 385
Google Scholar
[4] Li X, Zhang R J, Yu W J, Wang K L, Wei J Q, Wu D H, Cao A Y, Li Z H, Cheng Y, Zheng Q S, Ruoff R S, Zhu H W 2012 Sci. Rep. 2 870
Google Scholar
[5] Young R J, Kinloch I A, Gong L, Novoselov K S 2012 Compos. Sci. Technol. 72 1459
Google Scholar
[6] Gong L, Kinloch I A, Young R J, Riaz I, Jalil R, Novoselov K S 2010 Adv. Mater. 22 2694
Google Scholar
[7] Jiang T, Huang R, Zhu Y 2014 Adv. Funct. Mater. 24 396
Google Scholar
[8] Xu C C, Xue T, Guo J G, Qin Q H, Wu S, Song H B, Xie H M 2015 J. Appl. Phys. 117 164301
Google Scholar
[9] Xu C C, Xue T, Guo J G, Kang Y L, Qiu W, Song H B, Xie H M 2015 Mater. Lett. 161 755
Google Scholar
[10] 仇巍, 张启鹏, 李秋, 许超宸, 郭建刚 2017 66 166801
Google Scholar
Qiu W, Zhang Q P, Li Q, Xu C C, Guo J G 2017 Acta Phys. Sin. 66 166801
Google Scholar
[11] Cox H L 1952 Br. J. Appl. Phys. 3 72
Google Scholar
[12] Guo G D, Zhu Y 2015 J. Appl. Mech. 82 031005
Google Scholar
[13] Cui Z, Guo J G 2016 AIP Adv. 6 125110
Google Scholar
[14] Zhang S L, Li J C M 2004 J. Polym. Sci., Part B: Polym. Phys. 42 260
Google Scholar
[15] Kurennov S S 2014 Mech. Compos. Mater. 50 105
Google Scholar
[16] Mathias J D, Grédiac M, Balandraud X 2006 Int. J. Solids Struct. 43 6921
Google Scholar
[17] Randrianalisoa J, Dendievel R, Bréchet Y 2011 Compos. Part B: Eng. 42 2055
Google Scholar
[18] Park K, Paulino G H 2011 Appl. Mech. Rev. 64 060802
Google Scholar
[19] Dourado N, Silva F G A, de Moura M F S F 2018 Constr. Build. Mater. 176 14
Google Scholar
[20] Högberg J L 2006 Int. J. Fract. 141 549
Google Scholar
[21] Camanho P P, Davila C G, de Moura M F 2003 J. Compos. Mater. 37 1415
Google Scholar
[22] Faccio R, Denis P A, Pardo H, Goyenola C, Mombrú A W 2009 J. Phys. Condens. Matter 21 285304
Google Scholar
[23] 许超宸 2019 博士学位论文 (天津: 天津大学)
Xu C C 2019 Ph. D. Dissertation (Tianjin: Tianjin University) (in Chinese)
[24] Mohiuddin T M G, Lombardo A, Nair R R, Bonetti A, Savini G, Jalil R, Bonini N, Basko D M, Galiotis C, Marzari N, Novoselov K S, Geim A K, Ferrari A C 2009 Phys. Rev. B 79 205433
Google Scholar
[25] Sakata H, Dresselhaus G, Dresselhaus M S, Endo M 1988 J. Appl. Phys. 63 2769
Google Scholar
[26] Ni Z H, Yu T, Lu Y H, Wang Y Y, Feng Y P, Shen Z X 2008 ACS Nano 2 2301
Google Scholar
[27] Yu T, Ni Z H, Du C L, You Y M, Wang Y Y, Shen Z X 2008 J. Phys. Chem. C 112 12602
[28] Koukaras E N, Androulidakis C, Anagnostopoulos G, Papagelis K, Galiotis C 2016 Extreme Mech. Lett. 8 191
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 21933
- PDF Downloads: 296
- Cited By: 0
