-
With the development of laser technology, the application scope of nondiffracting beams, such as Bessel beams, Mathieu beams, cosine beams, and parabolic beams, which remain invariant along their propagation, continues to expand. During its propagation, the main lobes of these beams tend to bend towards off-axis position, which is called self-accelerating (or self-bending) property. A Bessel-like beam with self-acceleration can realize the propagation of the main lobe along a curved trajectory while maintaining the non-diffraction. Because of the above property, Bessel-like beams have been utilized in various areas such as guiding particles along arbitrarily curved trajectories, self-accelerating beams in nonlinear medium, plasma guidance, and laser-assisted guiding of electric discharges around objects. In this paper, we propose a method of bending the trajectory of Bessel-like beams by using a magnetic fluid deformable mirror (MFDM) instead of traditional spatial light modulator (SLM) and Pancharatnam-Berry (PB) phase manipulation. The MFDM provides a method without pixelation, where all parameters can be rapidly modified for fine-tuning. Furthermore, compared with the conventional deformable mirror, the MFDM has the advantages of a continuous and smooth mirror surface, large shape deformation, low manufacture cost, easy extension, and large inter-actuator stroke. Therefore, it is easy for the MFDM to generate the ideal shape of an axicon. Firstly, according to geometric analysis, the asymmetrical mirror profile to produce a self-accelerating Bessel-like optical beam is proposed. The proposed mirror profile can be used to compensate for the difference in optical path length for each annular slice of the axicon. If a collimated Gaussian beam is incident on the mirror combining the axicon and the asymmetrical mirror profiles, which can obtain Bessel-like beams with arbitrarily curved trajectories. Secondly, the resultant of the self-accelerating Bessel-like beams along parabolic trajectories is validated by the simulation in MATLAB. Finally, a prototype of MFDM consisting of the dual-layer arrays of miniature electromagnetic coils, a Maxwell coil and the magnetic fluid filled in a circular container is fabricated for the experiment. The experimental results show that the Bessel-like beams propagate along the parabolic trajectories, with the MFDM used, and the accuracy of the curved trajectories is verified. The proposed method in this paper opens a new experimental way to the study of Bessel-like beam; the theoretical approach can also be generalized mathematically for other non-paraxial beam propagation. -
Keywords:
- magnetic fluid /
- deformable mirror /
- nondiffracting beam /
- Bessel beam
[1] Durnin J 1987 J. Opt. Soc. 4 651
Google Scholar
[2] Hu Y, Nie J, Sun K, Ye Q, Wang L 2017 Opt. Commun. 394 108
Google Scholar
[3] Nadgaran H, Fallah R 2015 Opt. Commun. 341 160
Google Scholar
[4] Dolev I, Libster A, Arie A 2012 Appl. Phys. Lett. 101 101109
Google Scholar
[5] Siviloglou G A, Christodoulides D N 2007 Opt. Lett. 32 979
Google Scholar
[6] Zhao J, Zhang P, Deng D, Liu J, Gao Y, Chremmos I D, Efremidis N K, Christodoulides D N, Chen Z 2013 Opt. Lett. 38 498
Google Scholar
[7] Chremmos I D, Chen Z, Christodoulides D N, Efremidis N K 2012 Opt. Lett. 37 5003
Google Scholar
[8] Jarutis V, Matijošius A, Di Trapani P, Piskarskas A 2009 Opt. Lett. 34 2129
Google Scholar
[9] Zhao Z, Zang W, Tian J 2016 J. Optics-UK 18 025607
Google Scholar
[10] Dolev I, Kaminer I, Shapira A, Segev M, Arie A 2012 Phys. Rev. Lett. 108 113903
Google Scholar
[11] Polynkin P, Kolesik M, Moloney J V, Siviloglou G A, Christodoulides D N 2009 Science 324 229
Google Scholar
[12] Clerici M, Hu Y, Lassonde P, Milián C, Couairon A, Christodoulides D N, Chen Z, Razzari L, Vidal F, Légaré F, Faccio D, Morandotti R 2015 Sci. Adv. 1 e1400111
[13] Durnin J, Miceli Jr J J, Eberly J H 1987 Phys. Rev. Lett. 58 1499
Google Scholar
[14] Vieira T A, Zamboni-Rached M, Gesualdi M R 2014 Opt. Commun. 315 374
Google Scholar
[15] Herman R M, Wiggins T A 1991 J. Opt. Soc. Am. A 8 932
Google Scholar
[16] Cox A J, Dibble D C 1992 J. Opt. Soc. Am. A 9 282
Google Scholar
[17] Dudutis J, GeČys P, RaČiukaitis G 2016 Opt. Express 24 28433
Google Scholar
[18] Wu G, Wang F, Cai Y 2014 Phys. Rev. A 89 043807
Google Scholar
[19] 赵娟莹, 邓冬梅, 张泽, 刘京郊, 姜东升 2014 63 044204
Zhao J Y, Deng D M, Zhang Z, Liu J J, Jiang D S 2014 Acta Phys. Sin. 63 044204
[20] Chen J S, Jia J, Chu D 2017 Chin. Opt. Lett. 15 100901
Google Scholar
[21] 陈欢, 凌晓辉, 何武光, 李钱光, 易煦农 2017 66 044203
Chen H, Ling X H, He W G, Li Q G, Yi X N 2017 Acta Phys. Sin. 66 044203
[22] Wu Z, Iqbal A, Amara F B 2012 Modeling and Control of Magnetic Fluid Deformable Mirrors for Adaptive Optics Systems (Springer Science & Business Media)
[23] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[24] He Y, Liu Z, Liu Y, Zhou J, Ke Y, Luo H, Wen S 2015 Opt. Lett. 40 5506
Google Scholar
[25] Zhou J, Liu Y, Ke Y, Luo H, Wen S 2015 Opt. Lett. 40 3193
Google Scholar
[26] Liu Y, Ke Y, Zhou J, Liu Y, Luo H, Wen S, Fan D 2017 Sci. Rep. 7 44096
Google Scholar
[27] Pampaloni F, Enderlein J 2004 arXiv: physics/0410021
[28] Kamilov U S, Papadopoulos I N, Shoreh M H, Goy A, Vonesch C, Unser M, Psaltis D 2015 Optica 2 517
Google Scholar
[29] Brousseau D, Drapeau J, Piché M, Borra E F 2011 Appl. Opt. 50 4005
Google Scholar
[30] Wu Z, Kong X, Zhang Z, Wu J, Wang T, Liu M 2017 Micromachines 8 72
Google Scholar
[31] Yen Y T, Lu T Y, Lee Y C, Yu C C, Tsai Y C, Tseng Y C, Chen H L 2014 ACS Appl. Mater. Inter. 6 4292
Google Scholar
-
图 1 经叠加轮廓后弯曲类贝塞尔光束中心光瓣的传播轨迹(红色)
Figure 1. The propagation trajectory of the center lobe of a bended Bessel-like beam through the superimposed profile (in red).
图 2 偏移点几何关系分析 (a) 薄环上任意点与偏移点的光程; (b)偏移点与薄环的最长光程
Figure 2. Off-axis point geometric analysis: (a) The distance between any point on the thin ring and the off-axis point; (b) the longest distance between the off-axis point and the point on the thin ring.
图 3 镜面轮廓
Figure 3. Mirror profile.
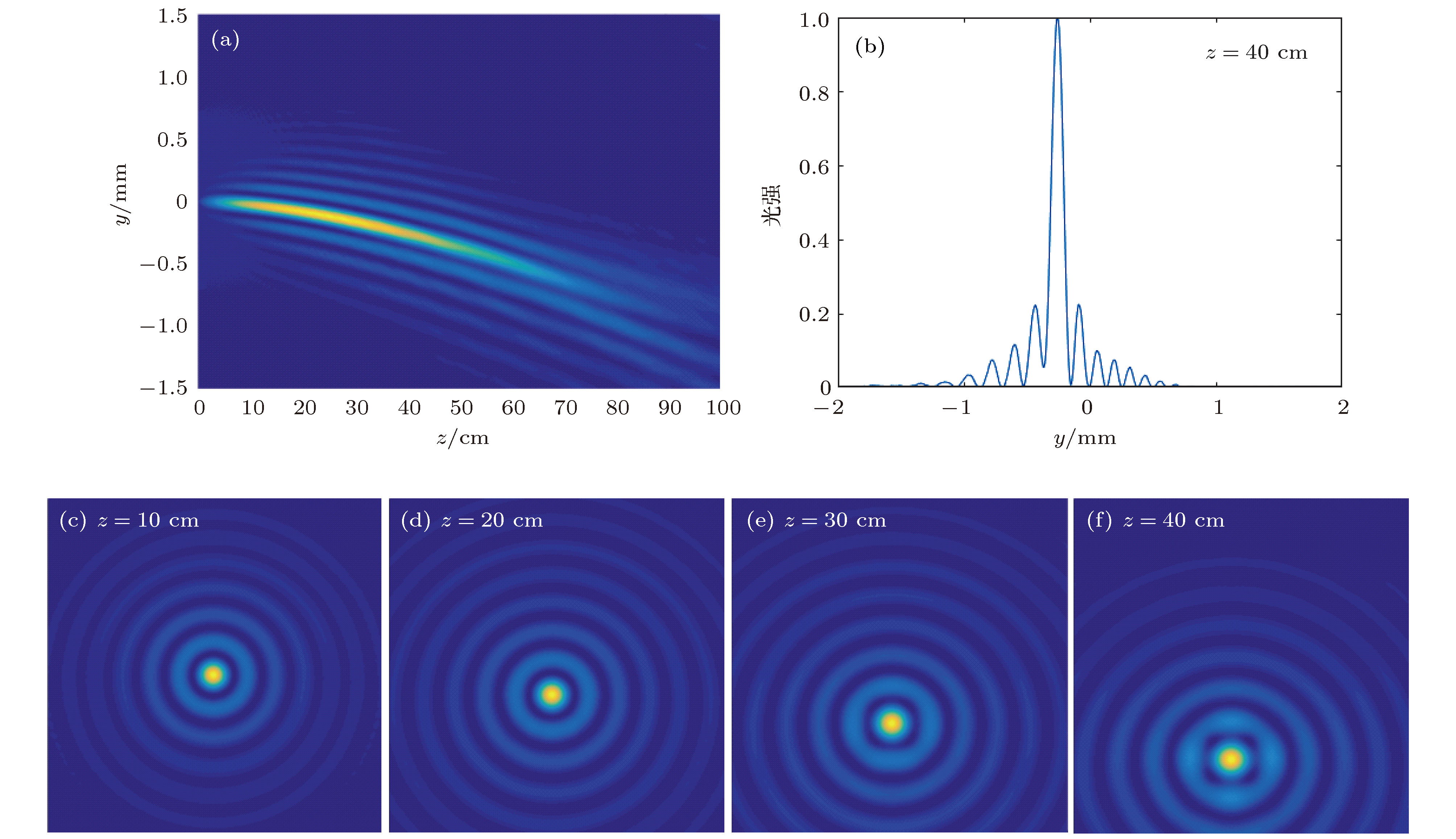
图 4 沿抛物线轨迹的自加速类贝塞尔光束仿真 (a) 数值模拟类贝塞尔光束传输的侧面图; (b) 弯曲轨迹类贝塞尔光束在传播距离
$z = 4{\rm{0 \;cm}}$ 处的光强; (c)—(f) 图(a)中不同传播距离处光强的横截面分布Figure 4. The simulation of self-accelerating Bessel-like beam along a parabolic trajectory: (a) Numerically simulated side-view propagation of the generated beam; (b) intensity of a bended Bessel-like beam when propagation distance
$z = 4{\rm{0 \;cm}}$ ; (c)−(f) cross-sectional images of Bessel-like beam along different distance.
图 5 磁液变形镜装置 (a) 实物图; (b) 结构示意图
Figure 5. Assembly of the prototype MFDM: (a) Actual diagram; (b) schematic diagram.
图 6 基于波前传感器的磁液变形镜镜面控制实验平台 (a) 光路示意图; (b) 实物图
Figure 6. Layout of the experimental system setup based on the wavefront sensor: (a) Schematic diagram of optical path; (b) actual diagram.
图 7 波前传感器检测到的波前轮廓(左图: 主视图; 右图: 三维视图) (a) 初始面形; (b)轴棱锥轮廓; (c) 镜面轮廓; (d) 混合轴棱锥和镜面轮廓后的面形轮廓
Figure 7. Wavefront detected by the wavefront sensor (left: main view; right: 3D view): (a) Initial wavefront; (b) an axicon profile; (c) mirror profile; (d) the combination of both axicon and mirror profile.
图 8 取四个不同z值的实验结果横截面图
Figure 8. Experimental cross-section profiles for four different values of z.
图 9 理论和实际测得的光束传播轨迹相比较
Figure 9. Comparison between numerical and experimental demonstrations of deflection of the central spot of a bended Bessel-like beam.
-
[1] Durnin J 1987 J. Opt. Soc. 4 651
Google Scholar
[2] Hu Y, Nie J, Sun K, Ye Q, Wang L 2017 Opt. Commun. 394 108
Google Scholar
[3] Nadgaran H, Fallah R 2015 Opt. Commun. 341 160
Google Scholar
[4] Dolev I, Libster A, Arie A 2012 Appl. Phys. Lett. 101 101109
Google Scholar
[5] Siviloglou G A, Christodoulides D N 2007 Opt. Lett. 32 979
Google Scholar
[6] Zhao J, Zhang P, Deng D, Liu J, Gao Y, Chremmos I D, Efremidis N K, Christodoulides D N, Chen Z 2013 Opt. Lett. 38 498
Google Scholar
[7] Chremmos I D, Chen Z, Christodoulides D N, Efremidis N K 2012 Opt. Lett. 37 5003
Google Scholar
[8] Jarutis V, Matijošius A, Di Trapani P, Piskarskas A 2009 Opt. Lett. 34 2129
Google Scholar
[9] Zhao Z, Zang W, Tian J 2016 J. Optics-UK 18 025607
Google Scholar
[10] Dolev I, Kaminer I, Shapira A, Segev M, Arie A 2012 Phys. Rev. Lett. 108 113903
Google Scholar
[11] Polynkin P, Kolesik M, Moloney J V, Siviloglou G A, Christodoulides D N 2009 Science 324 229
Google Scholar
[12] Clerici M, Hu Y, Lassonde P, Milián C, Couairon A, Christodoulides D N, Chen Z, Razzari L, Vidal F, Légaré F, Faccio D, Morandotti R 2015 Sci. Adv. 1 e1400111
[13] Durnin J, Miceli Jr J J, Eberly J H 1987 Phys. Rev. Lett. 58 1499
Google Scholar
[14] Vieira T A, Zamboni-Rached M, Gesualdi M R 2014 Opt. Commun. 315 374
Google Scholar
[15] Herman R M, Wiggins T A 1991 J. Opt. Soc. Am. A 8 932
Google Scholar
[16] Cox A J, Dibble D C 1992 J. Opt. Soc. Am. A 9 282
Google Scholar
[17] Dudutis J, GeČys P, RaČiukaitis G 2016 Opt. Express 24 28433
Google Scholar
[18] Wu G, Wang F, Cai Y 2014 Phys. Rev. A 89 043807
Google Scholar
[19] 赵娟莹, 邓冬梅, 张泽, 刘京郊, 姜东升 2014 63 044204
Zhao J Y, Deng D M, Zhang Z, Liu J J, Jiang D S 2014 Acta Phys. Sin. 63 044204
[20] Chen J S, Jia J, Chu D 2017 Chin. Opt. Lett. 15 100901
Google Scholar
[21] 陈欢, 凌晓辉, 何武光, 李钱光, 易煦农 2017 66 044203
Chen H, Ling X H, He W G, Li Q G, Yi X N 2017 Acta Phys. Sin. 66 044203
[22] Wu Z, Iqbal A, Amara F B 2012 Modeling and Control of Magnetic Fluid Deformable Mirrors for Adaptive Optics Systems (Springer Science & Business Media)
[23] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[24] He Y, Liu Z, Liu Y, Zhou J, Ke Y, Luo H, Wen S 2015 Opt. Lett. 40 5506
Google Scholar
[25] Zhou J, Liu Y, Ke Y, Luo H, Wen S 2015 Opt. Lett. 40 3193
Google Scholar
[26] Liu Y, Ke Y, Zhou J, Liu Y, Luo H, Wen S, Fan D 2017 Sci. Rep. 7 44096
Google Scholar
[27] Pampaloni F, Enderlein J 2004 arXiv: physics/0410021
[28] Kamilov U S, Papadopoulos I N, Shoreh M H, Goy A, Vonesch C, Unser M, Psaltis D 2015 Optica 2 517
Google Scholar
[29] Brousseau D, Drapeau J, Piché M, Borra E F 2011 Appl. Opt. 50 4005
Google Scholar
[30] Wu Z, Kong X, Zhang Z, Wu J, Wang T, Liu M 2017 Micromachines 8 72
Google Scholar
[31] Yen Y T, Lu T Y, Lee Y C, Yu C C, Tsai Y C, Tseng Y C, Chen H L 2014 ACS Appl. Mater. Inter. 6 4292
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 12191
- PDF Downloads: 100
- Cited By: 0
