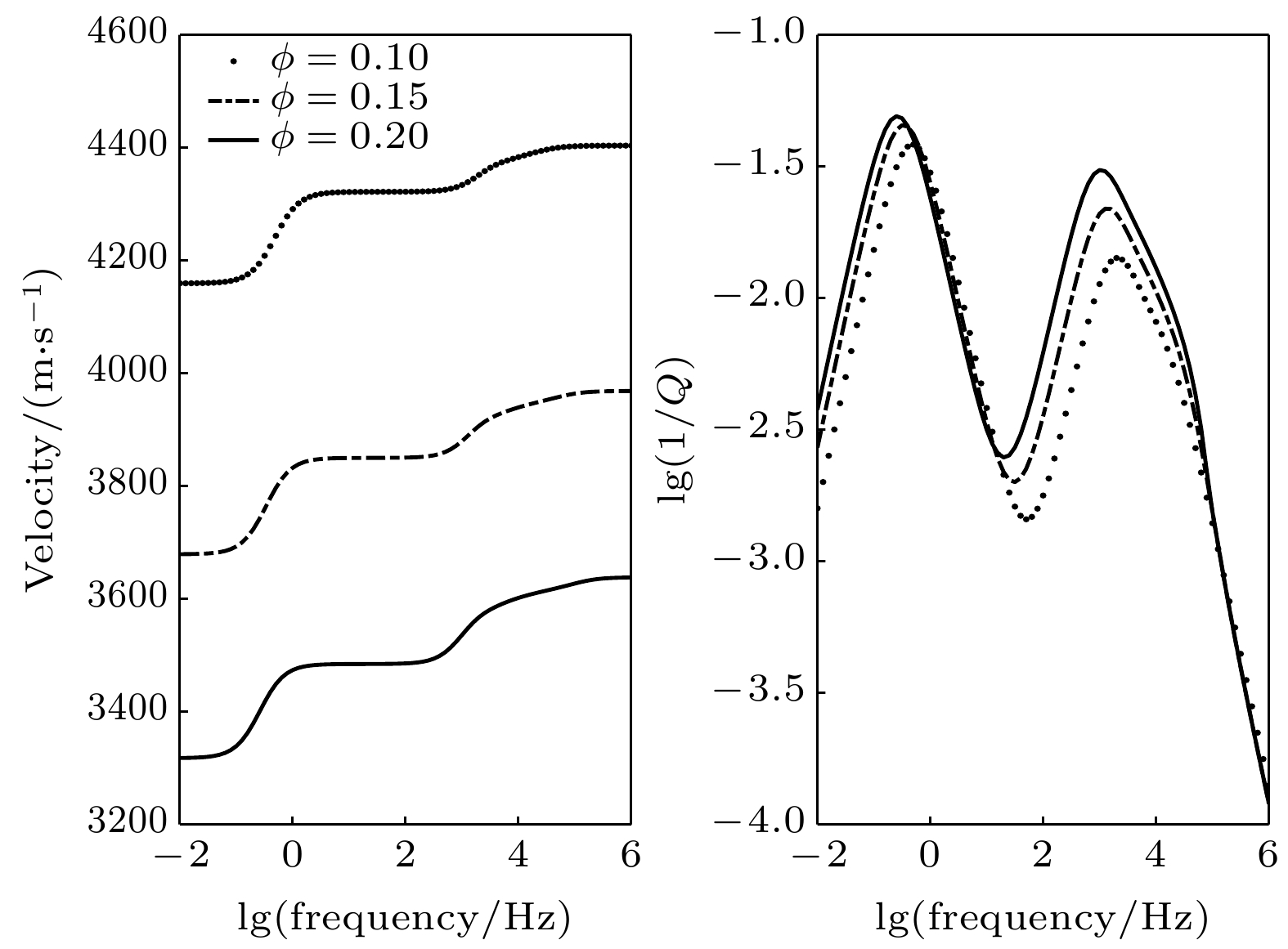
-
When elastic waves propagate in an unsaturated porous medium, the macro Biot flow, micro squirt flow, and meso flow will occur. The unsaturated porous medium is equivalent to the inclusion of gas phase porous fluid embedded in the background medium containing liquid phase porous fluid. Based on the unsaturated dual porous medium model, the micro squirt flow is introduced, and the wave propagation equation of unsaturated porous medium including macro, micro and mesoscopic scale wave introduced flow is established. The numerical analysis indicates that the model in this paper can better predict the wave velocity dispersion and attenuation in a wider frequency band.
[1] Biot M A 1941 J. Appl. Phys. 12 155
Google Scholar
[2] Biot M A 1956 J. Acoust. Soc. Am. 28 168
Google Scholar
[3] Biot M A 1962 J. Acoust. Soc. Am. 34 1254
Google Scholar
[4] Mavko G M 1979 J. Geophys. Res. 84 4769
Google Scholar
[5] Mavko G M, Nur A 1979 Geophysics 44 161
Google Scholar
[6] White J E 1975 Geophysics 40 224
Google Scholar
[7] White J E 1975 J. Acoust. Soc. Am. 57 S30
[8] Dutta N C 1979 Geophysics 44 1777
Google Scholar
[9] Dutta N C, Seriff A J 1979 Geophysics 24 1806
[10] Johnson D L 2001 J. Acoust. Soc. Am. 110 682
Google Scholar
[11] Pride S R, Berryman J G 2003 Phys. Rev. E 68 036604
Google Scholar
[12] Dvorkin J, Nur A 1993 Geophysics 4 524
[13] Li H X, Tao C H, Goloshubin G, Liu C, Shi S H, Huang G N, Zhang H, Zhang H, Zhang X F 2018 Acoust. Phys. 64 453
Google Scholar
[14] 杨顶辉, 陈小宏 2001 石油地球物理勘探 36 146
Google Scholar
Yang D H, Chen X H 2001 Oil Geophys. Prosp. 36 146
Google Scholar
[15] Diallo M S, Appel E 2000 J. Appl. Geophys. 44 313
Google Scholar
[16] 巴晶, Carcione J M, 曹宏, 杜启振, 袁振宇, 卢明辉 2012 地球 55 219
Google Scholar
Ba J, Carcione J M, Cao H, Du Q Z, Lu M H 2012 Chin. J. Geophys. 55 219
Google Scholar
[17] 巴晶 2010 中国科学: 物理学, 力学, 天文学 40 1398
Ba J 2010 Scientia Sinica: Phys, Mech & Astron 40 1398
[18] Ba J, Nie J X, Cao H, Yang H Z 2008 Geophys. Res. Lett. 35 L04303
[19] Ba J, Cao H, Yao F C, Yang N H 2008 Appl. Geophys. 5 261
Google Scholar
[20] Ba J, Carcione J M, Nie J X 2011 J. Geophys. Res. 116 B06202
[21] Zhao Z Y, Yin X Y, Zong Z Y 2018 Ann. Geophys. 61 SE343
[22] 胡亚元 2021 哈尔滨工业大学学报 53 160
Google Scholar
Hu Y Y 2021 J. Harbin Inst. Technol. 53 160
Google Scholar
[23] Rayleigh L 1917 Philos. Mag. 34 94
Google Scholar
[24] Achenbach J D 1984 Wave Propagation in Elastic Solids (Amsterdam: Elsevier Science) pp61–62
-
图 1 孔隙介质示意图 (a) 宏观尺度; (b) 介观尺度; (c) 微观尺度
Fig. 1. Schematic diagram of porous media: (a) Macro scale; (b) mesoscopic scale; (c) micro scale.
图 2 介观尺度孔隙介质等效特征单元 (a) 三维示意图; (b) 二维示意图
Fig. 2. Equivalent characteristic unit of mesoscopic porous media: (a) Three-dimensional schematic diagram; (b) two-dimensional schematic diagram.
图 3 不同孔隙介质模型波传播速度与衰减对比
Fig. 3. Comparison of wave propagation velocity and attenuation in porous media between different models.
图 4 不同孔隙度BRS模型预测的波速与衰减
Fig. 4. Wave velocity and attenuation predicted by BRS model with different porosity.
图 5 不同饱和度BRS模型预测的波速与衰减
Fig. 5. Wave velocity and attenuation predicted by BRS model with different saturation.
图 6 不同介观尺度BRS模型预测的波速与衰减
Fig. 6. Wave velocity and attenuation predicted by BRS model with different saturation.
图 7 不同渗透率BRS模型预测的波速与衰减
Fig. 7. Wave velocity and attenuation predicted by BRS model with different permeability
表 1 非饱和孔隙介质模型参数
Table 1. Parameters of unsaturated porous media model.
$ {\mu _{\text{b}}} $
/GPa$ {K_{\text{s}}} $
/GPa$ {K_{\text{b}}} $
/GPa$ K_{\text{f}}^{(1)} $
/GPa$ K_{\text{f}}^{(2)} $
/MPa$ {\rho _{\text{s}}} $
/(kg·m–3)$ \rho _{\text{f}}^{(1)} $
/(kg·m–3)14.6 38 16 2.25 0.1 2650 1000 $ \rho _{\text{f}}^{(2)} $/(kg·m–3) $ \phi $ $ \kappa $
/mD$ {\eta _1} $
/(Pa·s)$ {\eta _2} $
/(Pa·s)$ {v_1} $ $ {X_0} $
/m1 0.15 100 0.001 0.00001 0.95 0.25 
下载: 导出CSV
-
[1] Biot M A 1941 J. Appl. Phys. 12 155
Google Scholar
[2] Biot M A 1956 J. Acoust. Soc. Am. 28 168
Google Scholar
[3] Biot M A 1962 J. Acoust. Soc. Am. 34 1254
Google Scholar
[4] Mavko G M 1979 J. Geophys. Res. 84 4769
Google Scholar
[5] Mavko G M, Nur A 1979 Geophysics 44 161
Google Scholar
[6] White J E 1975 Geophysics 40 224
Google Scholar
[7] White J E 1975 J. Acoust. Soc. Am. 57 S30
[8] Dutta N C 1979 Geophysics 44 1777
Google Scholar
[9] Dutta N C, Seriff A J 1979 Geophysics 24 1806
[10] Johnson D L 2001 J. Acoust. Soc. Am. 110 682
Google Scholar
[11] Pride S R, Berryman J G 2003 Phys. Rev. E 68 036604
Google Scholar
[12] Dvorkin J, Nur A 1993 Geophysics 4 524
[13] Li H X, Tao C H, Goloshubin G, Liu C, Shi S H, Huang G N, Zhang H, Zhang H, Zhang X F 2018 Acoust. Phys. 64 453
Google Scholar
[14] 杨顶辉, 陈小宏 2001 石油地球物理勘探 36 146
Google Scholar
Yang D H, Chen X H 2001 Oil Geophys. Prosp. 36 146
Google Scholar
[15] Diallo M S, Appel E 2000 J. Appl. Geophys. 44 313
Google Scholar
[16] 巴晶, Carcione J M, 曹宏, 杜启振, 袁振宇, 卢明辉 2012 地球 55 219
Google Scholar
Ba J, Carcione J M, Cao H, Du Q Z, Lu M H 2012 Chin. J. Geophys. 55 219
Google Scholar
[17] 巴晶 2010 中国科学: 物理学, 力学, 天文学 40 1398
Ba J 2010 Scientia Sinica: Phys, Mech & Astron 40 1398
[18] Ba J, Nie J X, Cao H, Yang H Z 2008 Geophys. Res. Lett. 35 L04303
[19] Ba J, Cao H, Yao F C, Yang N H 2008 Appl. Geophys. 5 261
Google Scholar
[20] Ba J, Carcione J M, Nie J X 2011 J. Geophys. Res. 116 B06202
[21] Zhao Z Y, Yin X Y, Zong Z Y 2018 Ann. Geophys. 61 SE343
[22] 胡亚元 2021 哈尔滨工业大学学报 53 160
Google Scholar
Hu Y Y 2021 J. Harbin Inst. Technol. 53 160
Google Scholar
[23] Rayleigh L 1917 Philos. Mag. 34 94
Google Scholar
[24] Achenbach J D 1984 Wave Propagation in Elastic Solids (Amsterdam: Elsevier Science) pp61–62
下载:
计量
- 文章访问数: 7985
- PDF下载量: 137
- 被引次数: 0
