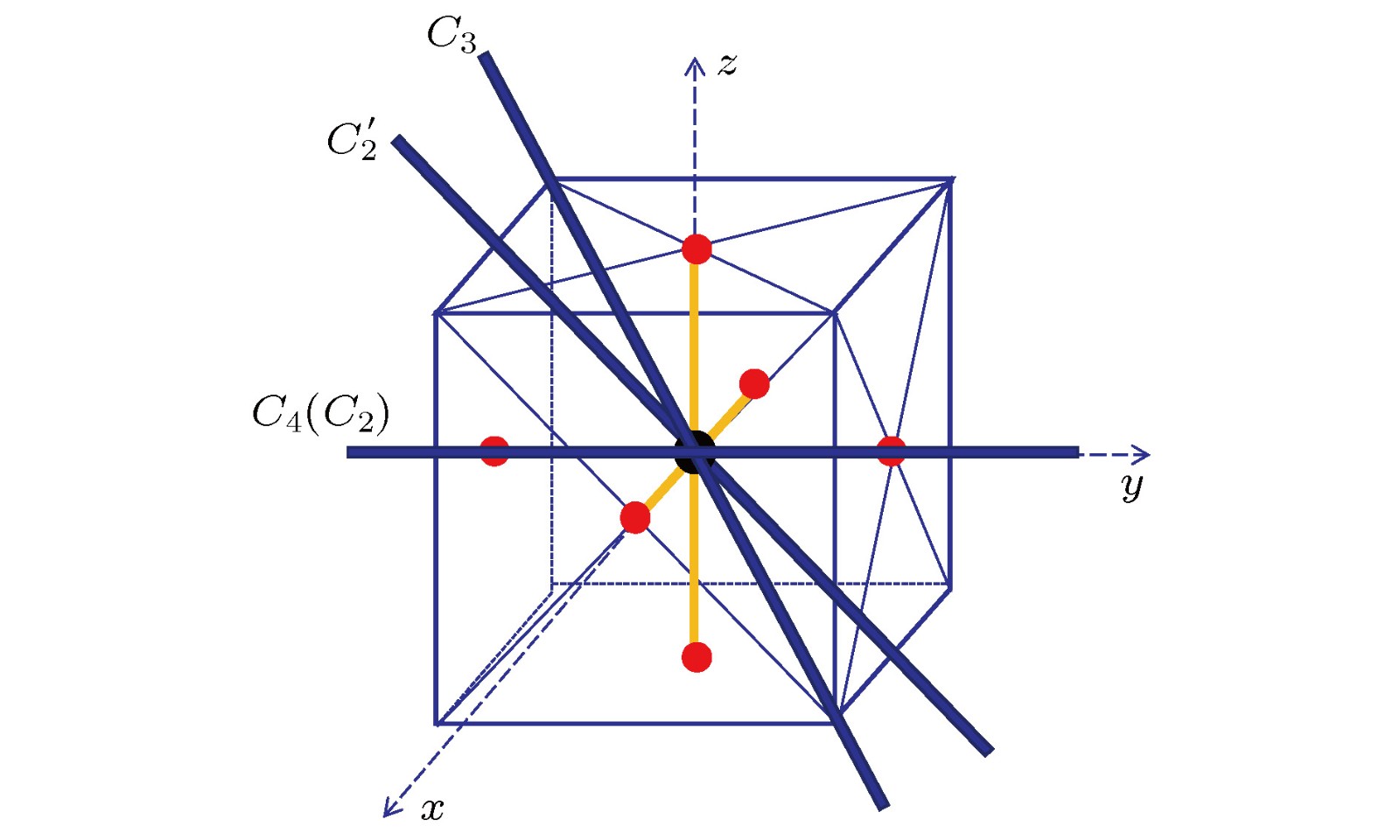
-
量化计算是理论研究分子的重要手段, 对于具有高对称群的分子, 采用子群计算是常用的方法. 分子的电子态或分子轨道等的对称性在子群的表示中会出现重迭, 从而不能从子群的结果直接给出电子态或分子轨道对称性的归属. 本文以如何判断
$ \rm {SF}_6 $ 基态$ ^1\rm A_{1\rm g} $ 的电子组态中最高占据轨道的对称性为例来解决这个问题. 针对某些文献中的$ \rm {SF}_6 $ 基态$ ^1\rm A_{1\rm g} $ 的电子组态中, 最高占据轨道对称性是$ T_{1g} $ 却写成$ T_{2g} $ 的问题, 采用Molpro量化计算软件, 对$ \rm {SF}_6 $ 基态的平衡结构, 进行了HF/6-311G*计算, 得到了能量三重简并的最高占据轨道的函数表达式, 进而运用$ O_h $ 群的对称操作作用在三个轨道函数上, 得到各操作的矩阵表示, 于是得到特征标, 最后确定了最高占据轨道为$ T_{1g} $ 对称性.Quantum chemical calculation is an important method to investigate the molecular structures for multi-atom molecules. The determination of electronic configurations and the accurate description of the symmetry of molecular orbitals are critical for understanding molecular structures. For the molecules belonging to high symmetry group, in the quantum chemical calculation the sub-group is always adopted. Thus the symmetries of some electric states or some molecular orbitals, which belong to different types of representations of high symmetry group, may coincide in the sub-group presentations. Therefore, they cannot be distinguished directly from the sub-group results. In this paper, we provide a method to identify the symmetry of molecular orbitals from the theoretical sub-group results and use this method to determine the symmetry of the highest occupied molecular orbitals (HOMO) of the sulfur hexafluoride SF6 molecule as an example. Especially, as a good insulating material, an important greenhouse gas and a hyper-valent molecule with the high octahedral$ O_h $ symmetry, SF6 has received wide attention for both the fundamental scientific interest and practical industrial applications. Theoretical work shows that the electronic configuration of ground electronic state$ ^1{\rm A_{1g}} $ of SF6 is${({\rm {core}})^{22}}{(4{\rm a_{1\rm g}})^2}{(3{{\rm t}_{1\rm u}})^6}{(2{{\rm e}_{\rm g}})^4}{(5{{\rm a}_{1\rm g}})^2}{(4{{\rm t}_{1\rm u}})^6}{(1{{\rm t}_{2\rm g}})^6}{(3{{\rm e}_{\rm g}})^4}{(1{{\rm t}_{2\rm u}})^6}{(5{{\rm t}_{1\rm u}})^6}{(1{{\rm t}_{1\rm g}})^6} $ and the symmetry of the HOMOs is$ T_{1g} $ . However, in some literature, the symmetry of HOMOs of SF6 has been written as$ T_{2g} $ instead of$ T_{1g} $ . The reason for this mistake lies in the fact that in the ab initial quantum chemical calculation used is the Abelian group$ D_{2h} $ , which is the sub-group of$ O_h $ , to describe the symmetries of molecular orbitals of SF6. However, there does not exist the one-to-one matching relationship between the representations of$ D_{2h} $ group and those of$ O_h $ group. For example, both irreducible representations$ T_{1g} $ and$ T_{2g} $ of$ O_h $ group are reduced to the sum of$ B_{1g} $ ,$ B_{2g} $ and$ B_{3g} $ of$ D_{2h} $ . So the symmetry of the orbitals needs to be investigated further to identify whether it is$ T_{1g} $ or$ T_{2g} $ . In this work, we calculate the orbital functions in the equilibrium structure of ground state of SF6 by using HF/6-311G* method, which is implemented by using the Molpro software. The expressions of the HOMO functions which are triplet degenerate in energy are obtained. Then by exerting the symmetric operations of$ O_h $ group on three HOMO functions, we obtain their matrix representations and thus their characters. Finally, the symmetry of the HOMOs is verified to be$ T_{1g} $ . By using this process, we may determine the molecular orbital symmetry of any other molecules with high symmetry group.-
Keywords:
- SF6 /
- the highest occupied molecular orbitals /
- molecule with high symmetry group /
- orbital's symmetry
[1] Tang B, Zhang L F, Han F Y, Luo Z C, Liang Q Q, Liu C Y, Zhu L P, Zhang J M 2018 AIP Adv. 8 015016
 Google Scholar
Google Scholar
[2] Zhang X, Gockenbach E, Liu Z L, Chen H B, Yang L H 2013 Electr. Power Syst. Res. 103 105
 Google Scholar
Google Scholar
[3] Okubo H, Beroual A 2011 IEEE Electr. Insul. M. 27 34
[4] Yoshino K, Hayashi S, Kohno Y, Kaneto K, Okube J, Moriya T 1984 Jpn. J. Appl. Phys. 23 L198
 Google Scholar
Google Scholar
[5] Tachikawa H, Yamano T 2001 Chem. Phys. 264 81
 Google Scholar
Google Scholar
[6] Ravishankara A R, Solomon S, Turnipseed A A, Warren R F 1993 Science 259 194
 Google Scholar
Google Scholar
[7] Niessen W V, Kraemer W P, Diercksen G H F 1979 Chem. Phys. Lett. 63 65
 Google Scholar
Google Scholar
[8] Christophorou L G, Olthoff J K 2000 J. Phys. Chem. Ref. Data 29 267
 Google Scholar
Google Scholar
[9] Decleva P, Fronzoni G, Kivimaki A, AlvarezRuiz J, Svensson S 2009 J. Phys. B: At. Mol. Opt. Phys. 42 055102
 Google Scholar
Google Scholar
[10] Jose J, Lucchese R R, Rescigno T N 2014 J. Chem. Phys. 140 481
[11] Hay P J 1977 J. Am. Chem. Soc. 8 1003
[12] Weigold E, Zheng Y 1991 Chem. Phys. 150 405
 Google Scholar
Google Scholar
[13] Li Y, Agrena H, Carravettab V, Vahtrasa O, Karlssonc L, Wannbergc B, Hollandd D M P, MacDonald M A 1998 J. Electron. Spectrosc. 94 163
 Google Scholar
Google Scholar
[14] Zhao M F, Shan X, Yang J, Wang E L, Niu S S , Chen X J 2015 Chin. J. Chem. Phys. 28 539
 Google Scholar
Google Scholar
[15] Watanabe N, Yamazaki M, Takahashi M 2016 J. Electron. Spectrosc. 209 78
 Google Scholar
Google Scholar
[16] Hay P J 1982 J. Chem. Phys. 76 502
 Google Scholar
Google Scholar
[17] Tachikawa H 2002 J. Phys. B: At. Mol. Opt. Phys. 35 55
 Google Scholar
Google Scholar
[18] 徐亦庄 1988 分子光谱理论 (北京: 清华大学出版社) 第75页
Xu Y Z 1988 Theory of Molecular Spectroscopy (Beijing: Tsinghua University Press) p75 (in Chinese)
[19] Werner H J, Knowles P J, Lindh R, Manby F R, Schutz M, Celani P, Korona T, Rauhut G, Amos R D, Bernhardsson A, Berning A, Cooper D L, Deegan M J O, Dobbyn A J, Eckert F, Hampel C, Hetzer G, Lloyd A W, McNicholas S J, Meyer W, Mura M E, Nicklass A, Palmieri P, et al. Molpro, A Package of ab initio Programs (Version 2006.1) http://www.molpro.net [2018-12-12 ]
[20] Delhommelle J, Boutio A, Tavitian B, Mackie A D, Fuchs A H 1999 Mol. Phys. 96 719
 Google Scholar
Google Scholar
[21] Krishnan R, Binkley J S, Seeger R, Pople J A 1979 J. Chem. Phys. 72 650
-
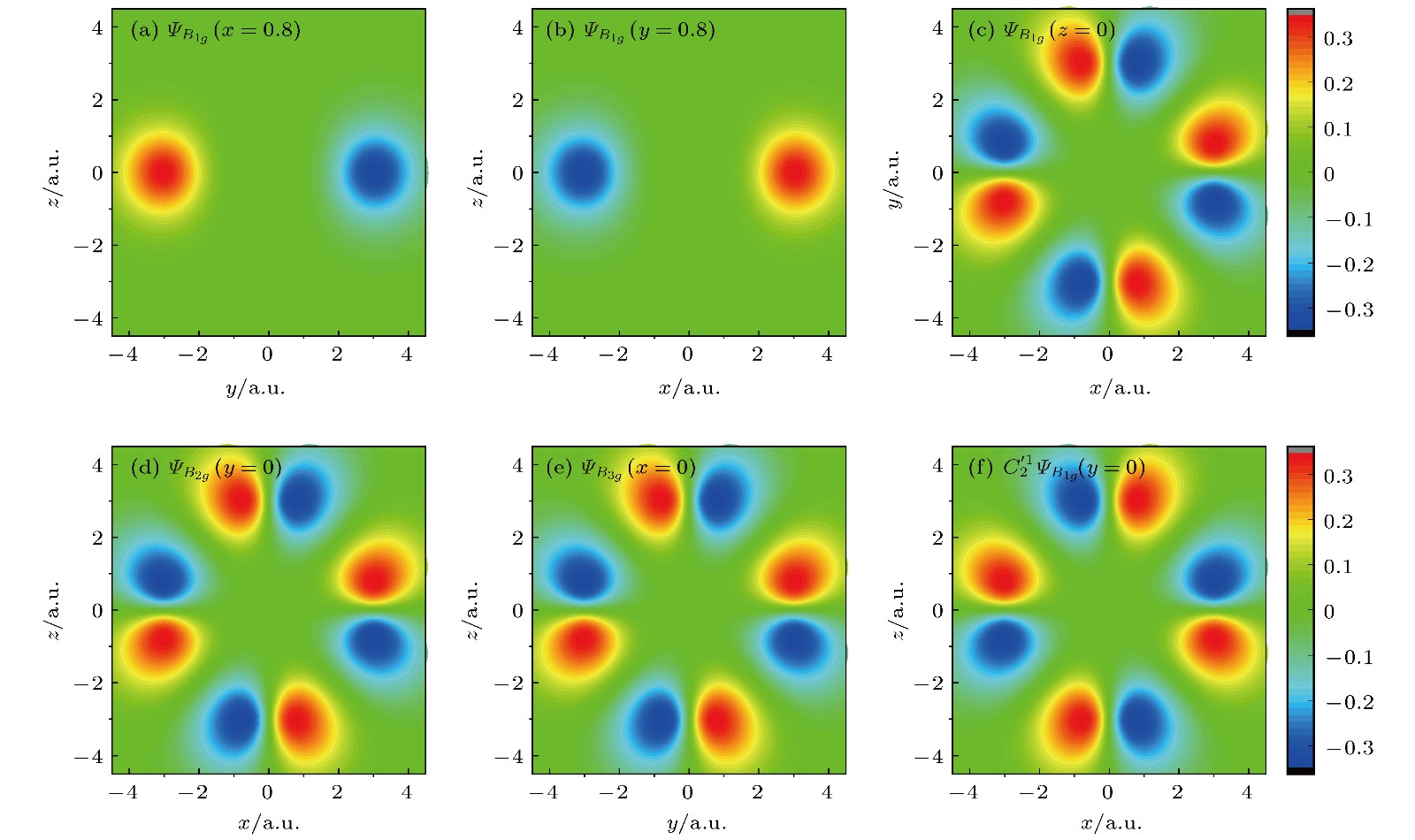
图 1
$\varPsi_{B_{1g}}$ ,$\varPsi_{B_{2g}}$ 和$\varPsi_{B_{3g}}$ 波函数截面图 (a)$\varPsi_{B_{1g}}$ 在x = 0.8 a.u.处的yz截面图; (b)$\varPsi_{B_{1g}}$ 在y = 0.8 a.u.处的xz截面图; (c)$\varPsi_{B_{1g}}$ 在z = 0 a.u.处的xy截面图;(d)$\varPsi_{B_{2g}}$ 在y = 0 a.u.处的xz截面图; (e)$\varPsi_{B_{3g}}$ 在x = 0 a.u.处的yz截面图; (f)$C_2'^1$ 作用在$\varPsi_{B_{1g}}$ 后取y = 0 a.u.处的xz截面图Fig. 1. Functions of
$\varPsi_{B_{1g}}$ ,$\varPsi_{B_{2g}}$ and$\varPsi_{B_{3g}}$ : (a)$\varPsi_{B_{1g}}$ in the yz plane for x = 0.8 a.u.; (b)$\varPsi_{B_{1g}}$ in the xz plane for y = 0.8 a.u.; (c)$\varPsi_{B_{1g}}$ in the xy plane for z = 0 a.u.; (d)$\varPsi_{B_{2g}}$ in the xz plane for y = 0 a.u.; (e)$\varPsi_{B_{3g}}$ in the yz plane for x = 0 a.u.; (f) the function obtained by acting$C_2'^1$ on$\varPsi_{B_{1g}}$ in the xz plane for y = 0 a.u..表 1 SF6的分子结构
Table 1. Molecular structure of SF6
k xk/a.u. yk/a.u. zk/a.u. S 1 0 0 0 F 2 2.923 0 0 F 3 –2.923 0 0 F 4 0 2.923 0 F 5 0 –2.923 0 F 6 0 0 2.923 F 7 0 0 –2.923 表 2 6-311G*基组中高斯函数的参数表
Table 2. Parameters of Gaussian functions of 6-311G* basis
i 1 2 3 4 5 6 ci 0.035461 0.237451 0.820458 1.0 1.0 1.0 αi/a.u. 55.4441 12.6323 3.71756 1.16545 0.321892 1.75 表 3
$O_h$ 群的部分特征标表Table 3. Part of character table of
$O_h$ group$O_h$ E $8C_3$ $6C_2'$ $6C_4$ $3C_2$ P $6S_4$ $8S_6$ $3\sigma_h$ $6\sigma_d$ $T_{1g}$ 3 0 –1 1 –1 3 1 0 –1 –1 $T_{2g}$ 3 0 1 –1 –1 3 –1 0 –1 1 -
[1] Tang B, Zhang L F, Han F Y, Luo Z C, Liang Q Q, Liu C Y, Zhu L P, Zhang J M 2018 AIP Adv. 8 015016
 Google Scholar
Google Scholar
[2] Zhang X, Gockenbach E, Liu Z L, Chen H B, Yang L H 2013 Electr. Power Syst. Res. 103 105
 Google Scholar
Google Scholar
[3] Okubo H, Beroual A 2011 IEEE Electr. Insul. M. 27 34
[4] Yoshino K, Hayashi S, Kohno Y, Kaneto K, Okube J, Moriya T 1984 Jpn. J. Appl. Phys. 23 L198
 Google Scholar
Google Scholar
[5] Tachikawa H, Yamano T 2001 Chem. Phys. 264 81
 Google Scholar
Google Scholar
[6] Ravishankara A R, Solomon S, Turnipseed A A, Warren R F 1993 Science 259 194
 Google Scholar
Google Scholar
[7] Niessen W V, Kraemer W P, Diercksen G H F 1979 Chem. Phys. Lett. 63 65
 Google Scholar
Google Scholar
[8] Christophorou L G, Olthoff J K 2000 J. Phys. Chem. Ref. Data 29 267
 Google Scholar
Google Scholar
[9] Decleva P, Fronzoni G, Kivimaki A, AlvarezRuiz J, Svensson S 2009 J. Phys. B: At. Mol. Opt. Phys. 42 055102
 Google Scholar
Google Scholar
[10] Jose J, Lucchese R R, Rescigno T N 2014 J. Chem. Phys. 140 481
[11] Hay P J 1977 J. Am. Chem. Soc. 8 1003
[12] Weigold E, Zheng Y 1991 Chem. Phys. 150 405
 Google Scholar
Google Scholar
[13] Li Y, Agrena H, Carravettab V, Vahtrasa O, Karlssonc L, Wannbergc B, Hollandd D M P, MacDonald M A 1998 J. Electron. Spectrosc. 94 163
 Google Scholar
Google Scholar
[14] Zhao M F, Shan X, Yang J, Wang E L, Niu S S , Chen X J 2015 Chin. J. Chem. Phys. 28 539
 Google Scholar
Google Scholar
[15] Watanabe N, Yamazaki M, Takahashi M 2016 J. Electron. Spectrosc. 209 78
 Google Scholar
Google Scholar
[16] Hay P J 1982 J. Chem. Phys. 76 502
 Google Scholar
Google Scholar
[17] Tachikawa H 2002 J. Phys. B: At. Mol. Opt. Phys. 35 55
 Google Scholar
Google Scholar
[18] 徐亦庄 1988 分子光谱理论 (北京: 清华大学出版社) 第75页
Xu Y Z 1988 Theory of Molecular Spectroscopy (Beijing: Tsinghua University Press) p75 (in Chinese)
[19] Werner H J, Knowles P J, Lindh R, Manby F R, Schutz M, Celani P, Korona T, Rauhut G, Amos R D, Bernhardsson A, Berning A, Cooper D L, Deegan M J O, Dobbyn A J, Eckert F, Hampel C, Hetzer G, Lloyd A W, McNicholas S J, Meyer W, Mura M E, Nicklass A, Palmieri P, et al. Molpro, A Package of ab initio Programs (Version 2006.1) http://www.molpro.net [2018-12-12 ]
[20] Delhommelle J, Boutio A, Tavitian B, Mackie A D, Fuchs A H 1999 Mol. Phys. 96 719
 Google Scholar
Google Scholar
[21] Krishnan R, Binkley J S, Seeger R, Pople J A 1979 J. Chem. Phys. 72 650
计量
- 文章访问数: 11924
- PDF下载量: 89
- 被引次数: 0
















































 下载:
下载: