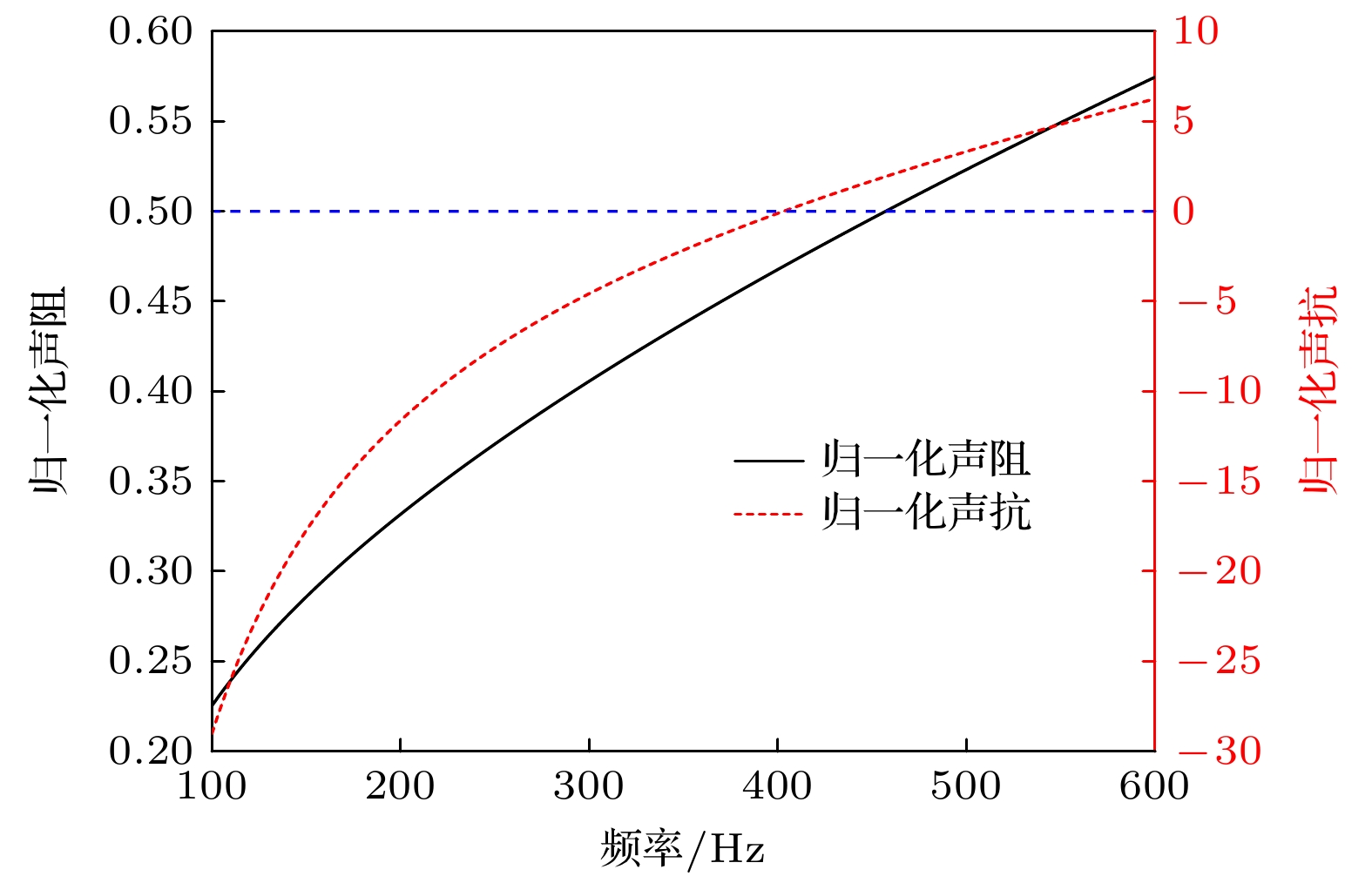
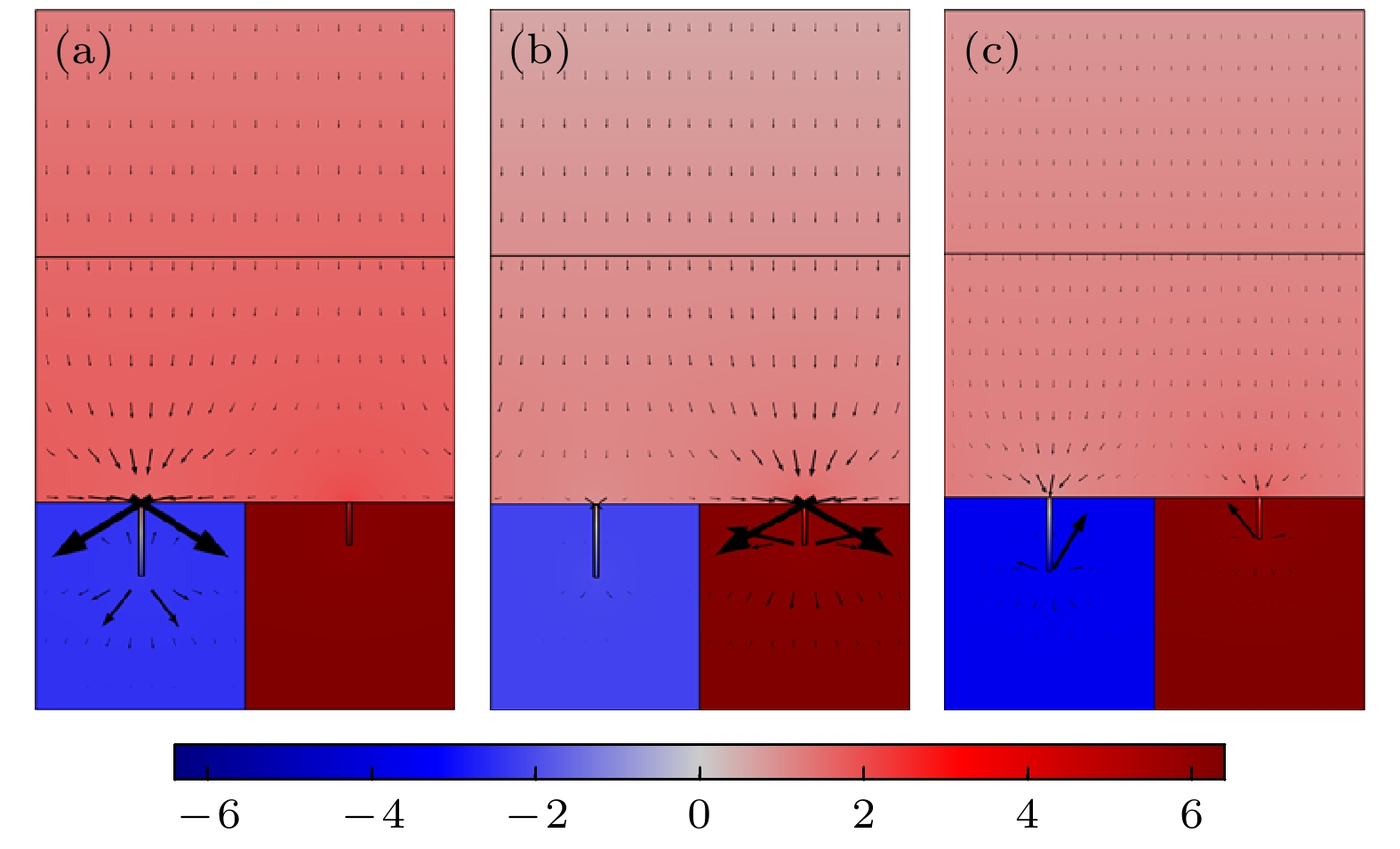
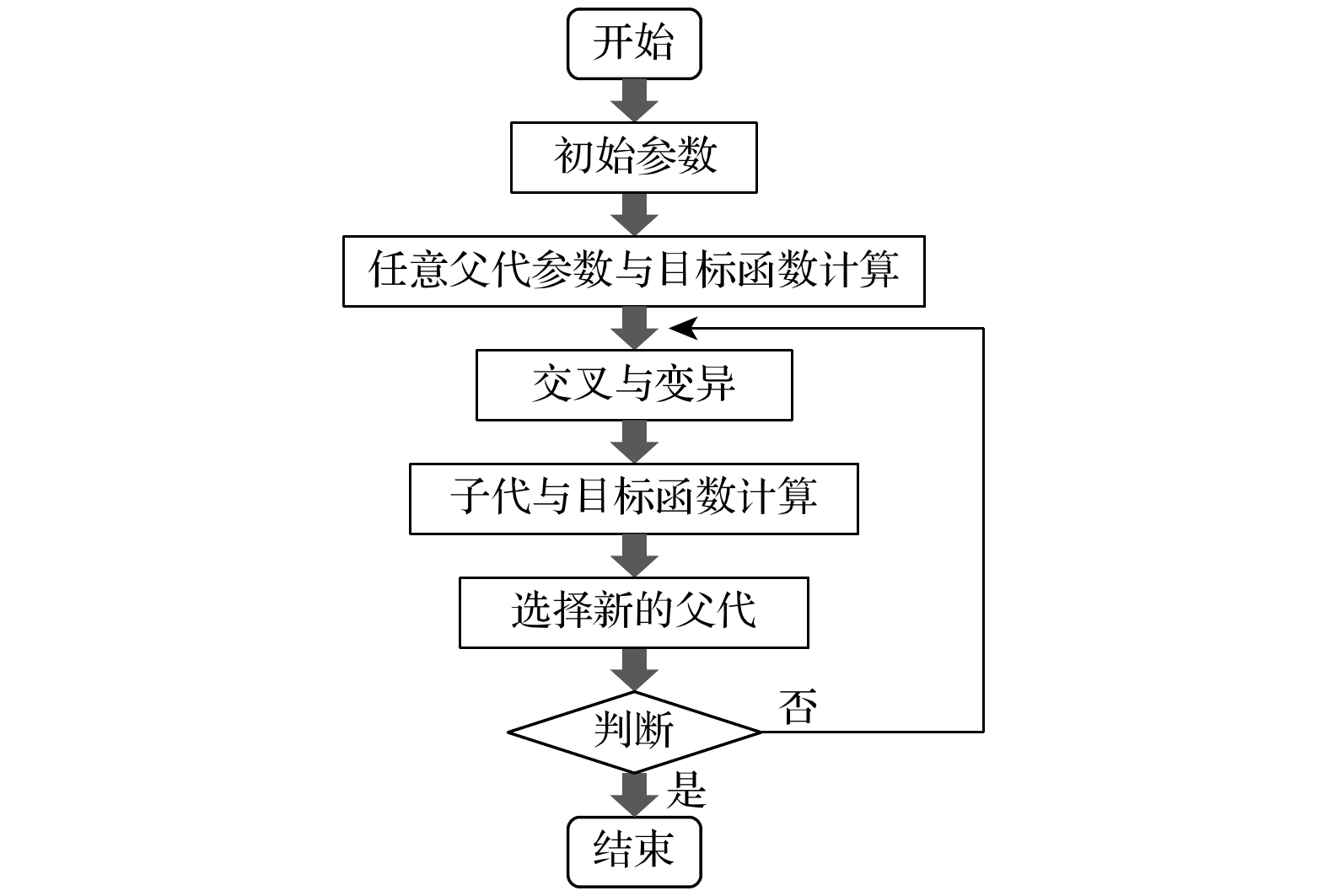
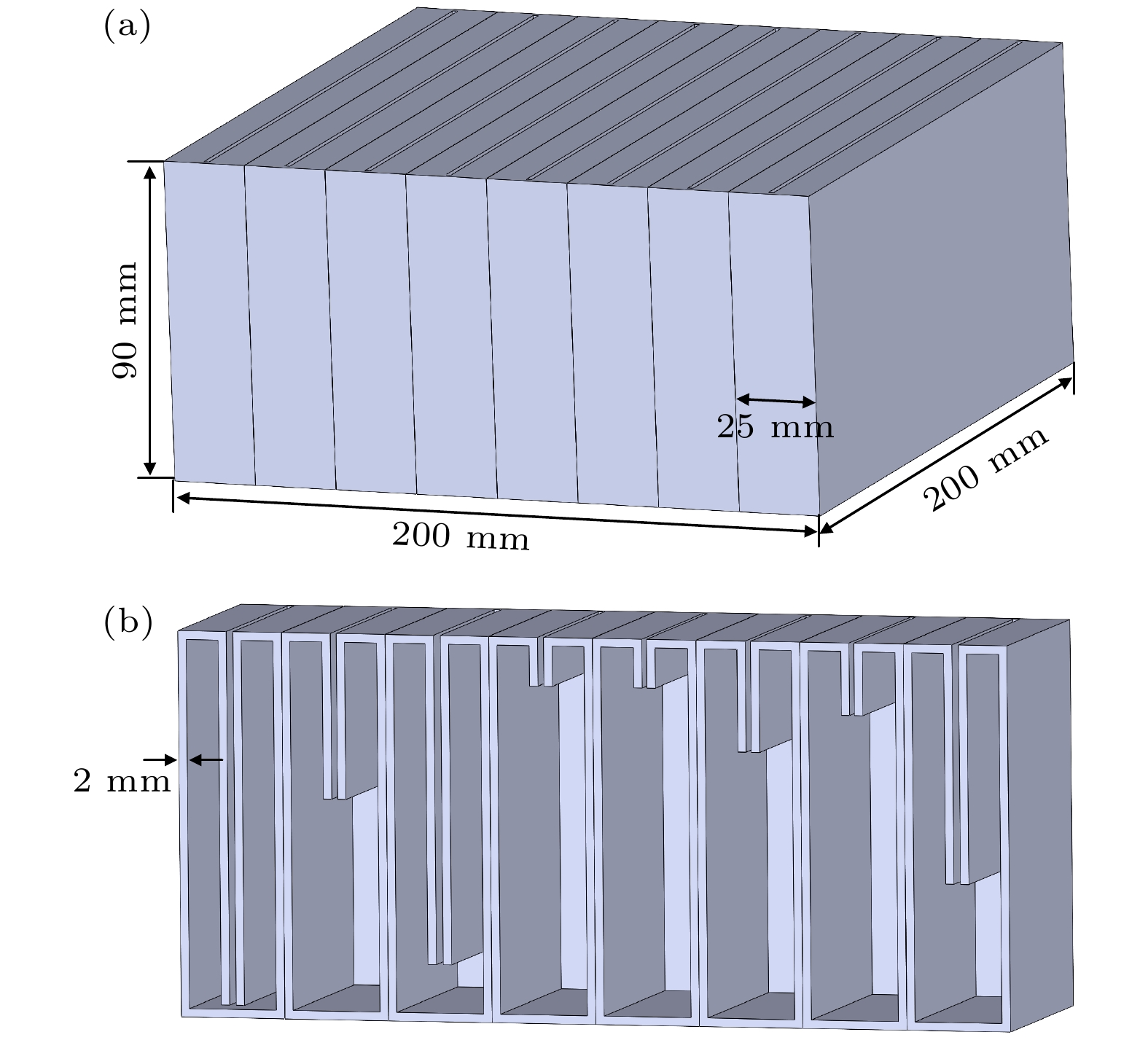
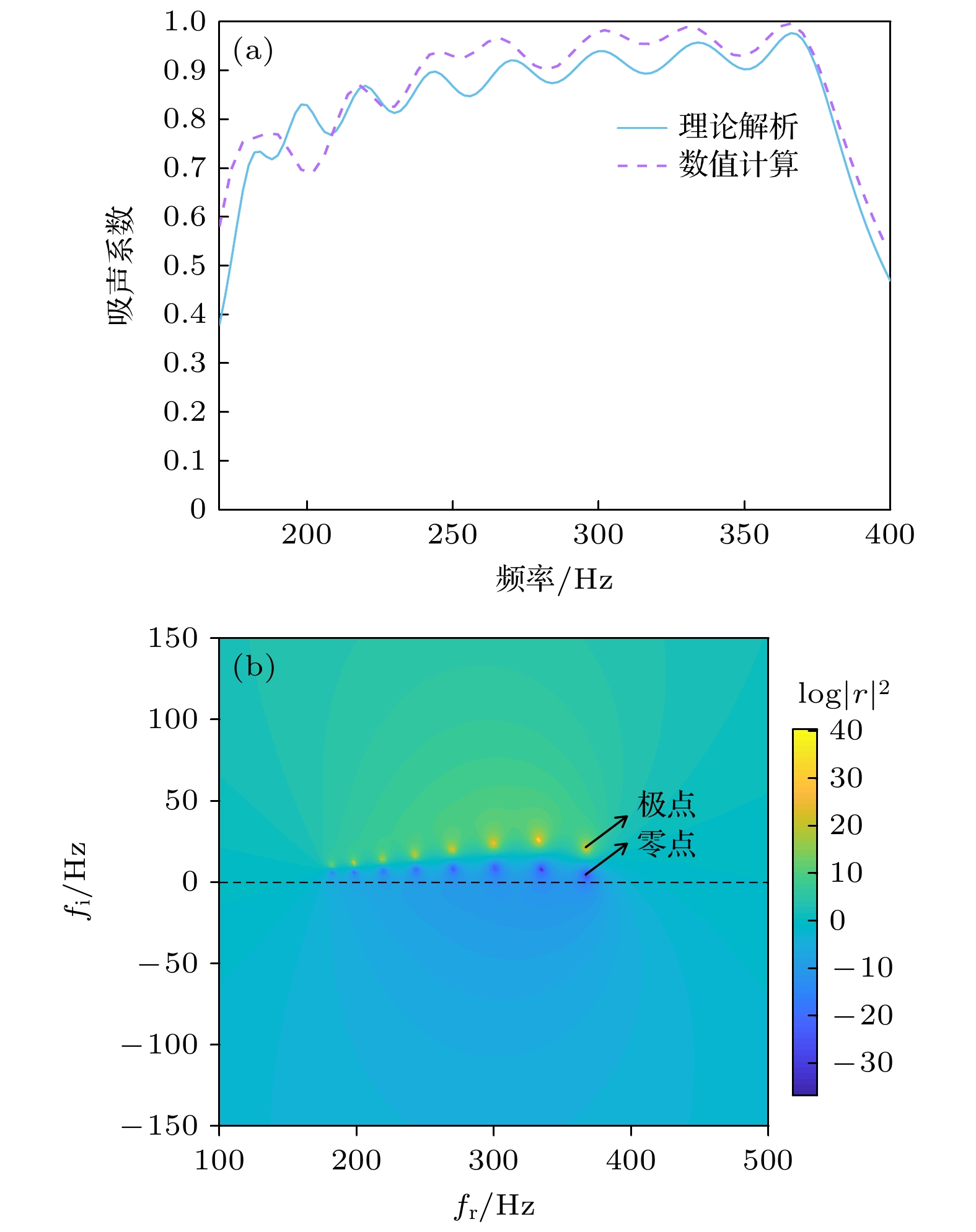
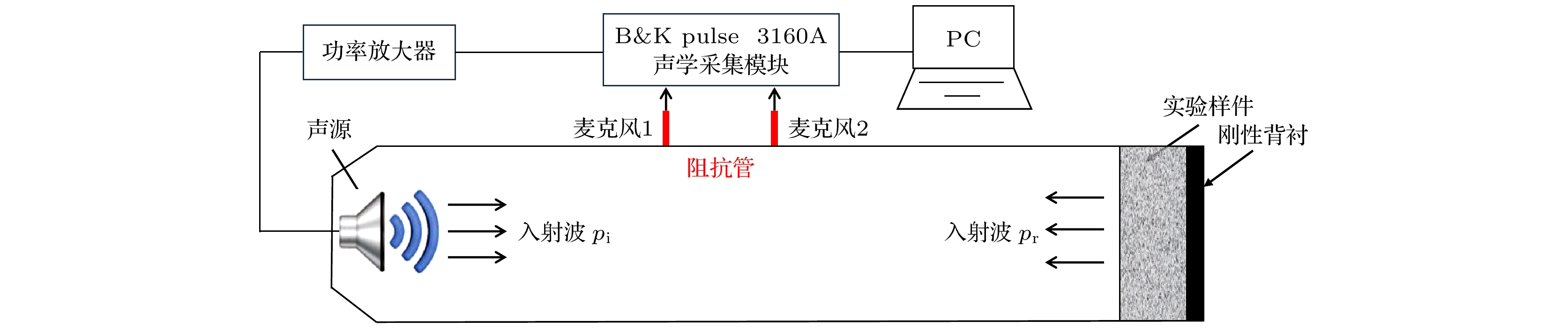
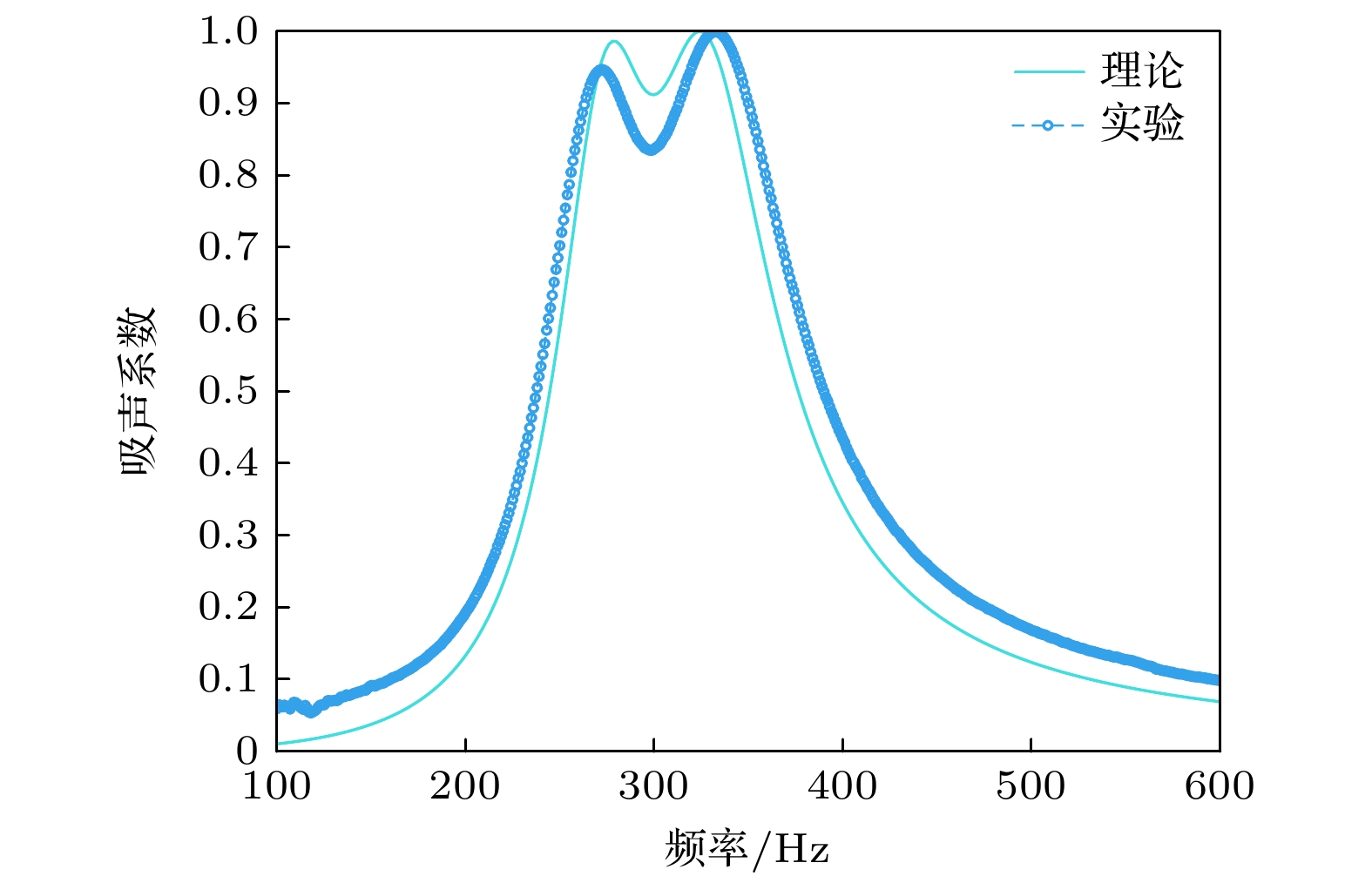
-
Low-frequency noise has always been a thorny problem in the field of noise control. In recent years, the development of sound-absorbing metastructures has provided new ideas for controlling low-frequency noise. In this work, we propose a low-frequency sound-absorbing metastructure constructed by Helmholtz resonators with embedded slit. Analytical and numerical models are established to analyze the sound absorption performance and mechanism of the proposed sound-absorbing metastructure, and optimization design is conducted to achieve low-frequency wideband absorption performance. The analytical modeling method and the performance of the proposed sound-absorbing metastructure are also experimentally verified. The main conclusions are summarized as follows. 1) By using transfer matrix method and finite element method, analytical and numerical models for calculating sound absorption coefficient are established. It is shown that analytical predictions are in good agreement with numerical calculations. It is demonstrated that a typical design of a 30-mm-thick single-cell metastructure can achieve a sound absorption coefficient of 0.88 at 404 Hz. Typical designs of two-cell parallel structure and the four-cell parallel structure (both with a thickness of 50 mm) can achieve two and four nearly perfect low-frequency sound absorption peaks in a frequency band of 200–400 Hz, respectively. 2) The low-frequency sound absorption mechanisms of the proposed metastructures are explained from four aspects: simplified equivalent model parameters, normalized acoustic impedance, complex-plane zero/pole distribution, and sound pressure cloud image and particle velocity field distribution. It is demonstrated that the main sound absorption mechanism is related to the thermal viscous loss of sound waves, caused by the inner wall of embedded slit. 3) The design for broadband low-frequency absorption performance is optimized by using differential evolution optimization algorithm. An optimized parallel-multi-cell coupled metastructure with multiple perfect sound absorption peaks below 500 Hz is realized. For a thickness of 90 mm, the sound absorption coefficient curve of an optimized metastructure exhibits 8 almost perfect sound absorption peaks and an average sound absorption coefficient of 0.86 in a frequency range of 170－380 Hz. 4) Experimental samples are fabricated to test sound absorption. Experimental results are basically consistent with the analytical predictions. The results from analytical model, numerical calculations and experimental measurements are mutually verified. In summary, the sound-absorbing metastructures with a thickness of sub-wavelength, proposed in this work, exhibit outstanding sound absorption performance at low frequencies. We demonstrate that they are suitable for low frequency broadband sound absorption below 500 Hz. Owing to their thin thickness and relatively simple construction, they have broad application prospects in practical noise control engineering. -
Keywords:
- sound-absorbing metastructure /
- Helmholtz resonator /
- embedded slit /
- low frequency absorption
[1] Champoux Y, Allard J F 1991 J. Appl. Phys. 70 1975
Google Scholar
[2] Panneton R 2007 J. Acoust. Soc. Am. 122 217
Google Scholar
[3] Trompette N, Barbry J, Sgard F, Nelisse H 2009 J. Acoust. Soc. Am. 125 31
Google Scholar
[4] Climente A, Torrent D, Sánchez-Dehesa J 2012 Appl. Phys. Lett. 100 144103
Google Scholar
[5] Ma G C, Sheng P 2016 Sci. Adv. 2 1501595
Google Scholar
[6] 肖勇, 王洋, 赵宏刚, 郁殿龙, 温激鸿 2023 机械工程学报 59 277
Google Scholar
Xiao Y, Wang Y, Zhao H G, Yu D L, Wen J H 2023 J. Mech. Eng. 59 277
Google Scholar
[7] Cai X B, Guo Q Q, Hu G K, Yang J 2014 Appl. Phys. Lett. 105 121901
Google Scholar
[8] Wang Y, Zhao H G, Yang H B, Zhong J, Zhao D, Lu Z L, Wen J H 2018 J. Appl. Phys. 123 185109
Google Scholar
[9] Wu F, Xiao Y, Yu D, Zhao H, Wang Y, Wen J 2019 Appl. Phys. Lett. 114 151901
Google Scholar
[10] 吴飞, 黄威, 陈文渊, 肖勇, 郁殿龙, 温激鸿 2020 69 134303
Google Scholar
Wu F, Huang W, Chen W Y, Xiao Y, Yu D L, Wen J H 2020 Acta Phys. Sin. 69 134303
Google Scholar
[11] Zhao H G, Wang Y, Yu D L, Yang H B, Zhong J, Wu F, Wen J H 2020 Compos. Struct. 239 111978
Google Scholar
[12] Jin Y B, Yang Y L, Wen Z H, He L S, Cang Y, Yang B, Djafari-Rouhani B, Li Y, Li Y 2022 Int. J. Mech. Sci. 226 107396
Google Scholar
[13] Liu C R, Yang Z R, Liu X L, Wu J H, Ma F Y 2023 APL Mater. 11 101122
Google Scholar
[14] 白宇, 张振方, 杨海滨, 蔡力, 郁殿龙 2023 72 054301
Google Scholar
Bai Y, Zhang Z F, Yang H B, Cai L, Yu D L 2023 Acta Phys. Sin. 72 054301
Google Scholar
[15] Liu J W, Yu D L, Yang H B, Shen H J, Wen J H 2020 Chin. Phys. Lett. 37 34301
Google Scholar
[16] Zhou Z L, Huang S B, Li D T, Zhu J, Li Y 2022 Natl. Sci. Rev. 9 171
Google Scholar
[17] Almeida G D N, Vergara E F, Barbosa L R, Lenzi A, Birch R S 2021 Appl. Acoust. 183 108312
Google Scholar
[18] Wu F, Ju Z G, Hu M, Zhang X, Li D, Liu K L 2023 J. Phys. D: Appl. Phys. 56 45401
Google Scholar
[19] Ma G C, Yang M, Xiao S W, Yang Z Y, Sheng P 2014 Nat. Mater. 13 873
Google Scholar
[20] Ge H, Yang M, Ma C, Lu M H, Chen Y F, Fang N, Sheng P 2018 Natl. Sci. Rev. 5 159
Google Scholar
[21] Cummer S A, Christensen J, Alù A 2016 Nat. Rev. Mater. 1 16001
Google Scholar
[22] Stinson M R 1991 J. Acoust. Soc. Am. 89 550
Google Scholar
[23] Verdière K, Panneton R, Elkoun S D, Dupont T, Leclaire P 2013 J. Acoust. Soc. Am. 134 4648
Google Scholar
[24] Guo J W, Zhang X, Fang Y, Jiang Z Y 2021 Compos. Struct. 260 113538
Google Scholar
[25] Tam C K W, Ju H, Jones M G, Watson W R, Parrott T L 2005 J. Sound Vib. 284 947
Google Scholar
[26] Zieliński T G, Chevillotte F, Deckers E 2019 Appl. Acoust. 146 261
Google Scholar
[27] 杜功焕, 朱哲民, 龚秀芬 2012 声学基础(南京: 南京大学出版社)第159页
Du G H, Zhu Z M, Gong X F 2012 Acoustics Foundation (Nanjing: Nanjing University Press) p159
[28] Romero-García V, Theocharis G, Richoux O, Merkel A, Tournat V, Pagneux V 2016 Sci. Rep. 6 19519
Google Scholar
[29] Lee F C, Chen W H 2001 J. Sound Vib. 248 621
Google Scholar
[30] Liu J, Herrin D W 2010 Appl. Acoust. 71 120
Google Scholar
[31] Ruiz H, Claeys C C, Deckers E, Desmet W 2016 Mech. Syst. Signal Pr. 70 904
[32] Romero-García V, Sánchez-Pérez J V, Garcia-Raffi L M 2011 J. Appl. Phys. 110 14904
Google Scholar
[33] Qamoshi K, Rasuli R 2016 Appl. Phys. A 122 788
Google Scholar
[34] Storn R, Price K 1997 J. Global Optim. 11 341
Google Scholar
-
图 1 内插缝Helmholtz共振吸声结构单元胞示意图
Figure 1. Schematic of single slit-embedded Helmholtz resonator.
图 2 矩形截面管道声传播示意图
Figure 2. Diagram of sound propagation in a rectangular section pipe.
图 3 并联结构示意图
Figure 3. Schematic diagram of parallel structure.
图 4 有限元模型 (a) 三维狭窄声学模型; (b) 二维狭窄声学模型; (c) 二维热黏性声学模型
Figure 4. Finite element model: (a) Three-dimensional simulation model of narrow acoustic; (b) two-dimensional simulation model of narrow acoustic; (c) two-dimensional simulation model of thermoviscous acoustic.
图 5 单元胞三维图
Figure 5. Three dimensional diagram of single cell.
图 6 单元胞吸声系数曲线
Figure 6. Sound absorption coefficient curve of single cell.
图 7 吸声系数曲线 (a) 随缝宽的变化; (b) 随缝高的变化
Figure 7. Sound absorption coefficient curve: (a) Vary with width of slit; (b) vary with height of slit.
图 8 双元胞与四元胞并联示意图
Figure 8. Three-dimensional diagram of two cells and four cells in parallel.
图 9 吸声系数曲线 (a) 双元胞并联结构; (b) 四元胞并联结构
Figure 9. Sound absorption coefficient curve: (a) Two cells in parallel; (b) four cells in parallel.
图 10 吸声频谱 (a) 随缝宽的变化; (b) 随缝高的变化
Figure 10. Absorption spectrum: (a) Vary with width of slit; (b) vary with height of slit.
图 11 归一化声阻抗曲线
Figure 11. Normalized acoustic impedance curve.
图 12 归一化声阻抗曲线 (a) 双元胞并联结构; (b) 四元胞并联结构
Figure 12. Normalized acoustic impedance curve: (a) Two cells in parallel; (b) four cells in parallel.
图 13 单元胞复平面反射系数与声压速度场分布
Figure 13. Zero-pole distribution of single cell on complex plane and distribution of sound pressure and velocity field.
图 14 反射系数在复平面的分布 (a) 双元胞结构; (b) 四元胞结构
Figure 14. Distribution of reflection coefficient log|r|2: (a) Two cells in parallel; (b) four cells in parallel.
图 15 声压及速度场分布 (a) 257 Hz; (b) 294 Hz; (c) 275 Hz
Figure 15. Sound pressure and velocity field distribution: (a) 257 Hz; (b) 294 Hz; (c) 275 Hz.
图 16 差分进化算法流程图
Figure 16. Flow chart of differential evolution algorithm.
图 17 八元胞并联三维图(厚度90 mm)
Figure 17. Three-dimensional diagram of eight cells in parallel (thickness 90 mm).
图 18 吸声系数曲线及复平面零极点分布
Figure 18. Sound absorption coefficient curve and distribution of reflection coefficient log|r|2.
图 19 实验测试系统示意图
Figure 19. Schematic diagram of experimental setup.
图 20 实验测试系统实物图
Figure 20. Photo of experimental setup.
图 21 实验样件实物照片
Figure 21. Photo of the experimental sample.
图 22 单元胞结构理论解析与实验测试吸声系数(样件1, 厚30 mm)
Figure 22. Comparison of theoretical and experimental sound absorption coefficient of single cell (Sample 1, thickness 30 mm).
图 25 多元胞并联理论解析与实验测试吸声系数(样件4, 厚90 mm)
Figure 25. Comparison of theoretical and experimental sound absorption coefficient of multiple cells in parallel (Sample 4, thickness 90 mm).
图 23 双元胞并联结构理论解析与实验测试吸声系数(样件2, 厚50 mm)
Figure 23. Comparison of theoretical and experimental sound absorption coefficient of two cells in parallel (Sample 2, thickness 50 mm).
图 24 四元胞并联结构理论解析与实验测试吸声系数(样件3, 厚50 mm)
Figure 24. Comparison of theoretical and experimental sound absorption coefficient of four cells in parallel (Sample 3, thickness 50 mm).
表 1 单个内插缝Helmholtz共振腔结构参数
Table 1. Structural parameters of single slit-embedded Helmholtz resonator.
长L/mm 宽D/mm 高H/mm 缝宽d/mm 缝高lr/mm 100 100 30 2 10 
DownLoad: CSV
表 2 双元胞并联结构参数
Table 2. Structural parameters of two cells in parallel.
长L/mm 宽D/mm 高H/mm 缝宽d1/mm 缝高lr1/mm 缝宽d2/mm 缝高lr2/mm 50 50 50 1.2 17.3 1.1 9.8
DownLoad: CSV
表 3 四元胞并联结构参数
Table 3. Structural parameters of four cells in parallel.
长L/mm 宽D/mm 高H/mm 缝宽d1/mm 缝高lr1/mm 缝宽d2/mm 缝高lr2/mm 缝宽d3/mm 缝高lr3/mm 缝宽d4/mm 缝高lr4/mm 50 50 50 2.7 42.3 1.7 17.9 1.3 8 1.3 4.7
DownLoad: CSV
表 4 多元胞并联结构参数
Table 4. Structural parameters of multivariate cells in parallel.
元胞 1 2 3 4 5 6 7 8 缝宽d/mm 1.5 1.4 1.7 1.4 1.1 1.2 1.1 1.5 缝高lr/mm 84 35.1 70.6 10.6 10.3 23.5 15.3 50.6
DownLoad: CSV
-
[1] Champoux Y, Allard J F 1991 J. Appl. Phys. 70 1975
Google Scholar
[2] Panneton R 2007 J. Acoust. Soc. Am. 122 217
Google Scholar
[3] Trompette N, Barbry J, Sgard F, Nelisse H 2009 J. Acoust. Soc. Am. 125 31
Google Scholar
[4] Climente A, Torrent D, Sánchez-Dehesa J 2012 Appl. Phys. Lett. 100 144103
Google Scholar
[5] Ma G C, Sheng P 2016 Sci. Adv. 2 1501595
Google Scholar
[6] 肖勇, 王洋, 赵宏刚, 郁殿龙, 温激鸿 2023 机械工程学报 59 277
Google Scholar
Xiao Y, Wang Y, Zhao H G, Yu D L, Wen J H 2023 J. Mech. Eng. 59 277
Google Scholar
[7] Cai X B, Guo Q Q, Hu G K, Yang J 2014 Appl. Phys. Lett. 105 121901
Google Scholar
[8] Wang Y, Zhao H G, Yang H B, Zhong J, Zhao D, Lu Z L, Wen J H 2018 J. Appl. Phys. 123 185109
Google Scholar
[9] Wu F, Xiao Y, Yu D, Zhao H, Wang Y, Wen J 2019 Appl. Phys. Lett. 114 151901
Google Scholar
[10] 吴飞, 黄威, 陈文渊, 肖勇, 郁殿龙, 温激鸿 2020 69 134303
Google Scholar
Wu F, Huang W, Chen W Y, Xiao Y, Yu D L, Wen J H 2020 Acta Phys. Sin. 69 134303
Google Scholar
[11] Zhao H G, Wang Y, Yu D L, Yang H B, Zhong J, Wu F, Wen J H 2020 Compos. Struct. 239 111978
Google Scholar
[12] Jin Y B, Yang Y L, Wen Z H, He L S, Cang Y, Yang B, Djafari-Rouhani B, Li Y, Li Y 2022 Int. J. Mech. Sci. 226 107396
Google Scholar
[13] Liu C R, Yang Z R, Liu X L, Wu J H, Ma F Y 2023 APL Mater. 11 101122
Google Scholar
[14] 白宇, 张振方, 杨海滨, 蔡力, 郁殿龙 2023 72 054301
Google Scholar
Bai Y, Zhang Z F, Yang H B, Cai L, Yu D L 2023 Acta Phys. Sin. 72 054301
Google Scholar
[15] Liu J W, Yu D L, Yang H B, Shen H J, Wen J H 2020 Chin. Phys. Lett. 37 34301
Google Scholar
[16] Zhou Z L, Huang S B, Li D T, Zhu J, Li Y 2022 Natl. Sci. Rev. 9 171
Google Scholar
[17] Almeida G D N, Vergara E F, Barbosa L R, Lenzi A, Birch R S 2021 Appl. Acoust. 183 108312
Google Scholar
[18] Wu F, Ju Z G, Hu M, Zhang X, Li D, Liu K L 2023 J. Phys. D: Appl. Phys. 56 45401
Google Scholar
[19] Ma G C, Yang M, Xiao S W, Yang Z Y, Sheng P 2014 Nat. Mater. 13 873
Google Scholar
[20] Ge H, Yang M, Ma C, Lu M H, Chen Y F, Fang N, Sheng P 2018 Natl. Sci. Rev. 5 159
Google Scholar
[21] Cummer S A, Christensen J, Alù A 2016 Nat. Rev. Mater. 1 16001
Google Scholar
[22] Stinson M R 1991 J. Acoust. Soc. Am. 89 550
Google Scholar
[23] Verdière K, Panneton R, Elkoun S D, Dupont T, Leclaire P 2013 J. Acoust. Soc. Am. 134 4648
Google Scholar
[24] Guo J W, Zhang X, Fang Y, Jiang Z Y 2021 Compos. Struct. 260 113538
Google Scholar
[25] Tam C K W, Ju H, Jones M G, Watson W R, Parrott T L 2005 J. Sound Vib. 284 947
Google Scholar
[26] Zieliński T G, Chevillotte F, Deckers E 2019 Appl. Acoust. 146 261
Google Scholar
[27] 杜功焕, 朱哲民, 龚秀芬 2012 声学基础(南京: 南京大学出版社)第159页
Du G H, Zhu Z M, Gong X F 2012 Acoustics Foundation (Nanjing: Nanjing University Press) p159
[28] Romero-García V, Theocharis G, Richoux O, Merkel A, Tournat V, Pagneux V 2016 Sci. Rep. 6 19519
Google Scholar
[29] Lee F C, Chen W H 2001 J. Sound Vib. 248 621
Google Scholar
[30] Liu J, Herrin D W 2010 Appl. Acoust. 71 120
Google Scholar
[31] Ruiz H, Claeys C C, Deckers E, Desmet W 2016 Mech. Syst. Signal Pr. 70 904
[32] Romero-García V, Sánchez-Pérez J V, Garcia-Raffi L M 2011 J. Appl. Phys. 110 14904
Google Scholar
[33] Qamoshi K, Rasuli R 2016 Appl. Phys. A 122 788
Google Scholar
[34] Storn R, Price K 1997 J. Global Optim. 11 341
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4039
- PDF Downloads: 443
- Cited By: 0
