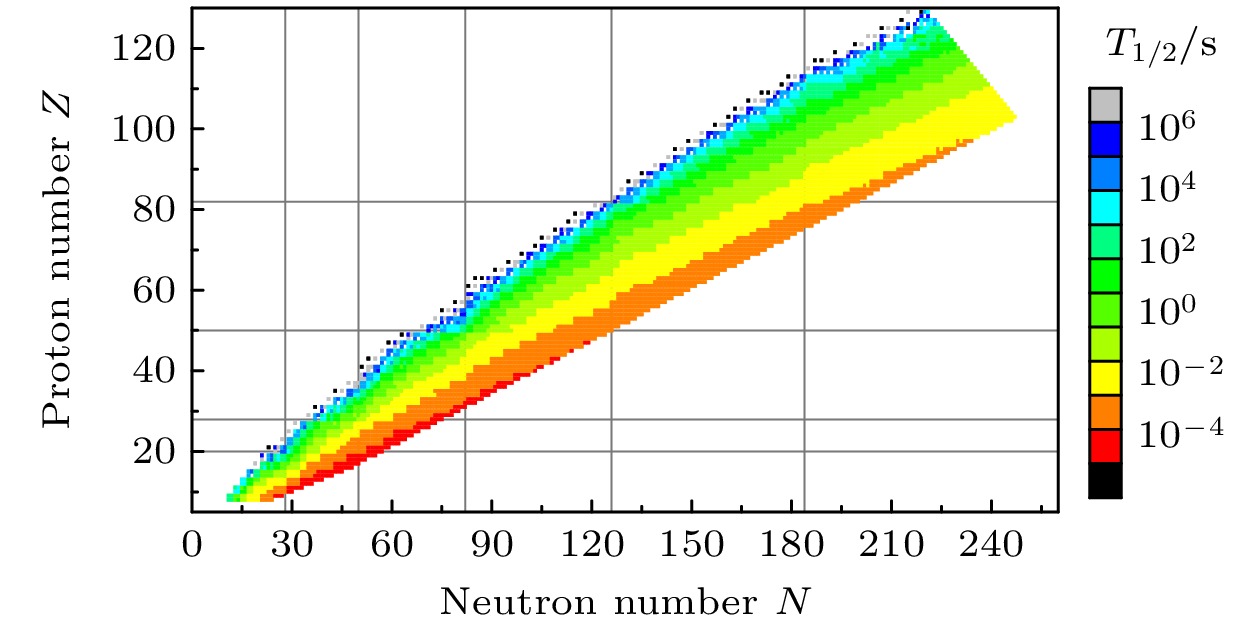
-
Nuclear β-decay half-lives play an important role not only in nuclear physics, but also in astrophysics. The β-decay half-lives of many nuclei involved in the astrophysical rapid neutron-capture (r -process) still cannot be measured experimentally, so the theoretical predictions of nuclear β-decay half-lives are inevitable for r-process studies. Theoretical models for studying the nuclear β-decay half-lives include the empirical formula, the gross theory, the quasiparticle random phase approximation (QRPA), and the shell model. Compared with other theoretical models of β-decay half-lives, the empirical formula has high computational efficiency, and its prediction accuracy can be improved by introducing more and more physical information. In this work, an empirical formula without free parameters is proposed to calculate the nuclear β-decay half-lives based on the Fermi theory of β decay. By including the pairing effect, the shell effect, and the isospin dependence, the newly proposed empirical formula significantly improves the accuracy of predicting the nuclear β-decay half-life. For the nuclei with half-lives less than 1 second, the root-mean-square deviation of the common logarithms of the nuclear β-decay half-life predicted by the new empirical formula from the experimental data decreases to 0.220, which is improved by about 54% compared with that by the empirical formula without free parameters, even better than those by other existing empirical formulas and microscopic QRPA approaches. In the unknown region, the nuclear β-decay half-lives predicted by the new empirical formula are generally shorter than those predicted by the microscopic models in the light nuclear region, while those predicted by the new empirical formula in the heavy nuclear region are generally in agreement with those predicted by the microscopic models. The half-lives of neutron-rich nuclei on the nuclear chart are then predicted by the new empirical formula, providing nuclear β-decay half-life inputs for the r-process simulations.
-
Keywords:
- β-decay half-lives /
- empirical formula /
- r-process
[1] Burbidge E M, Burbidge G R, Fowler W A, Hoyle F 1957 Rev. Mod. Phys. 29 547
Google Scholar
[2] Thielemann F K, Arcones A, Käappeli R, Liebendrfer M, Rauscher T, Winteler C, Fröhlichb C, Dillmannc I, Fischer T, Martinez-Pinedoc G, Langanke K, Farouqi K, Kratz K L, Panov I, Korneev I K 2011 Prog. Part. Nucl. Phys. 66 346
Google Scholar
[3] Cowan J J, Thielemann F K, Truran J W 1991 Phys. Rep. 208 267
Google Scholar
[4] Qian Y Z 2003 Prog. Part. Nucl. Phys. 50 153
Google Scholar
[5] Arnould M, Goriely S, Takahashi K 2007 Phys. Rep. 450 97
Google Scholar
[6] Chen J, Fang J Y, Hao Y W, Niu Z M, Niu Y F 2023 Astrophys. J. 943 102
Google Scholar
[7] Mumpower M R, Surmana R, McLaughlin G C, Aprahamian A 2016 Prog. Part. Nucl. Phys. 86 86
Google Scholar
[8] Li Z, Niu Z M, Sun B H 2019 Sci. China. Phys. Mech. Astron. 62 982011
Google Scholar
[9] Niu Z, Sun B, Meng J 2009 Phys. Rev. C 80 065806
Google Scholar
[10] Surman R, Engel J, Bennett J R, Meyer B S 1997 Phys. Rev. Lett. 79 1809
Google Scholar
[11] Zhang X P, Ren Z Z 2006 Phys. Rev. C 73 014305
Google Scholar
[12] Zhang X P, Ren Z Z, Zhi Q J, Zheng Q 2007 J. Phys. G: Nucl. Part. Phys. 34 2611
Google Scholar
[13] Zhou Y, Li Z H, Wang Y B, Chen Y S, Guo B, Su J, Li Y J, Yan S Q, Li X Y, Han Z Y, Shen Y P, Gan L, Zeng S, Lian G, Liu W P 2017 Sci. China-Phys. Mech. Astron. 60 082012
Google Scholar
[14] Takahashi K, Yamada M 1969 Prog. Theor. Phys. 41 1470
Google Scholar
[15] Tachibana T, Yamada M, Yoshida Y 1990 Prog. Theor. Phys. 84 641
Google Scholar
[16] Nakata H, Tachibana T, Yamada M 1997 Nucl. Phys. A 625 521
Google Scholar
[17] Koura H, Chiba S 2017 Phys. Rev. C 95 064304
Google Scholar
[18] Engel J, Bender M, Dobaczewski J, Surman R 1999 Phys. Rev. C 60 014302
Google Scholar
[19] Minato F, Bai C L 2013 Phys. Rev. Lett. 110 122501
Google Scholar
[20] Niu Z M, Niu Y F, Liang H Z, Long W H, Nikšić T, Vretenar D, Meng J 2013 Phys. Lett. B 723 172
Google Scholar
[21] Borzov I N, Goriely S 2000 Phys. Rev. C 62 035501
Google Scholar
[22] Langanke K, Martínez-Pinedo G 2003 Rev. Mod. Phys. 75 819
Google Scholar
[23] Martínez-Pinedo G, Langanke K 1999 Phys. Rev. Lett. 83 4502
Google Scholar
[24] Suzuki T, Yoshida T, Kajino T, Otsuka T 2012 Phys. Rev. C 85 015802
Google Scholar
[25] Zhi Q, Caurier E, Cuenca-García J J, Langanke K, Martínez-Pinedo G, Sieja K 2013 Phys. Rev. C 87 025803
Google Scholar
[26] Möller P, Pfeiffer B, Kratz K L 2003 Phys. Rev. C 67 055802
Google Scholar
[27] Minato F, Niu Z, Liang H 2022 Phys. Rev. C 106 024306
Google Scholar
[28] Marketin T, Huther L, Martinez-Pinedo G 2016 Phys. Rev. C 93 025805
Google Scholar
[29] Niu Z M, Niu Y F, Liu Q, Liang H Z, Guo J Y 2013 Phys. Rev. C 87 051303
Google Scholar
[30] Wang Z Y, Niu Y F, Niu Z M, Guo J Y 2016 J. Phys. G: Nucl. Part. Phys. 43 045108
Google Scholar
[31] Nakatsukasa T, Inakura T, Yabana K 2007 Phys. Rev. C 76 024318
Google Scholar
[32] Liang H Z, Nakatsukasa T, Niu Z M, Meng J 2013 Phys. Rev. C 87 054310
Google Scholar
[33] Ney E M, Engel J, Li T, Schunck N 2020 Phys. Rev. C 102 034326
Google Scholar
[34] Mustonen M T, Engel J 2016 Phys. Rev. C 93 014304
Google Scholar
[35] Endo F, Koura H 2019 Phys. Rev. C 99 034303
Google Scholar
[36] Fang J Y, Chen J, Niu Z M 2022 Phys. Rev. C 106 054318
Google Scholar
[37] Sargent B W 1933 Proc. R. Soc. Lond. A 139 659
Google Scholar
[38] Shi M, Fang J Y, Niu Z M 2021 Chin. Phys. C 45 044103
Google Scholar
[39] Uyen N K, Chae K Y, Duy N N, Ly N D 2022 J. Phys. G: Nucl. Part. Phys. 49 025201
Google Scholar
[40] Kondev F G, Wang M, Huang W J, Naimi S, Audi G 2021 Chin. Phys. C 45 030001
Google Scholar
[41] Fermi E 1934 Z. Phys. 88 161
Google Scholar
[42] Wang N, Liu M, Wu X, Meng J 2014 Phys. Lett. B 734 215
Google Scholar
[43] Möller P, Mumpower M R, Kawano T, Myers W D 2019 At. Data Nucl. Data Tables 125 1
Google Scholar
-
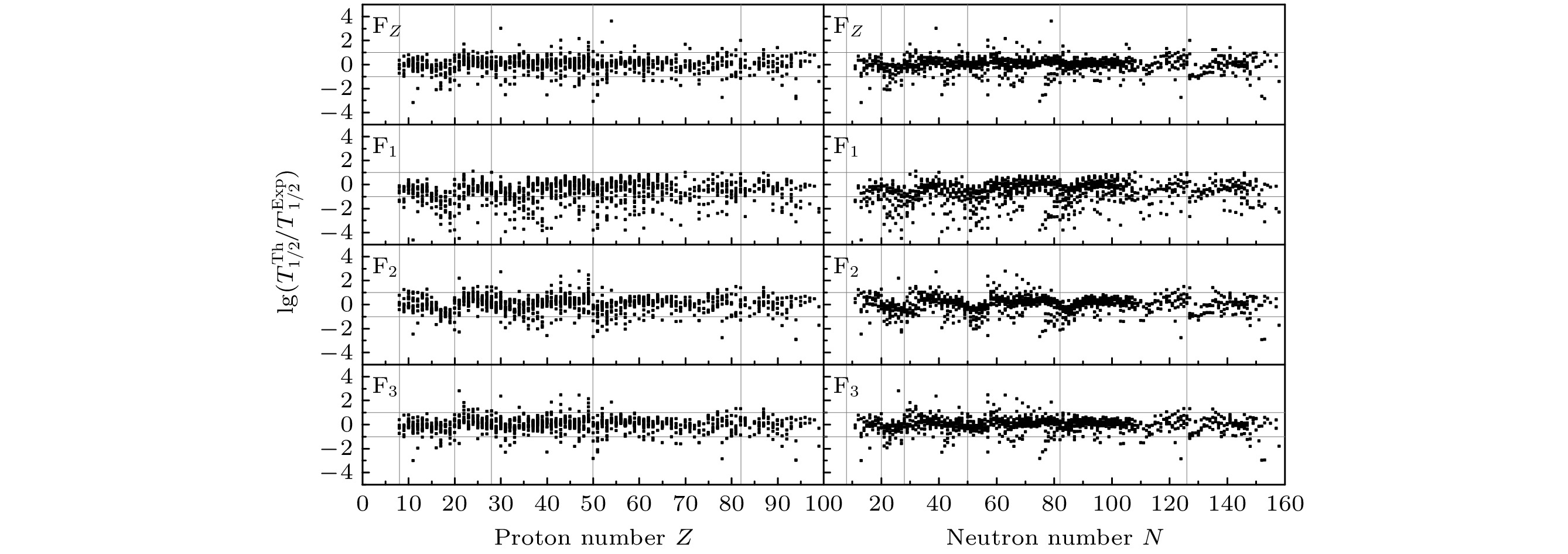
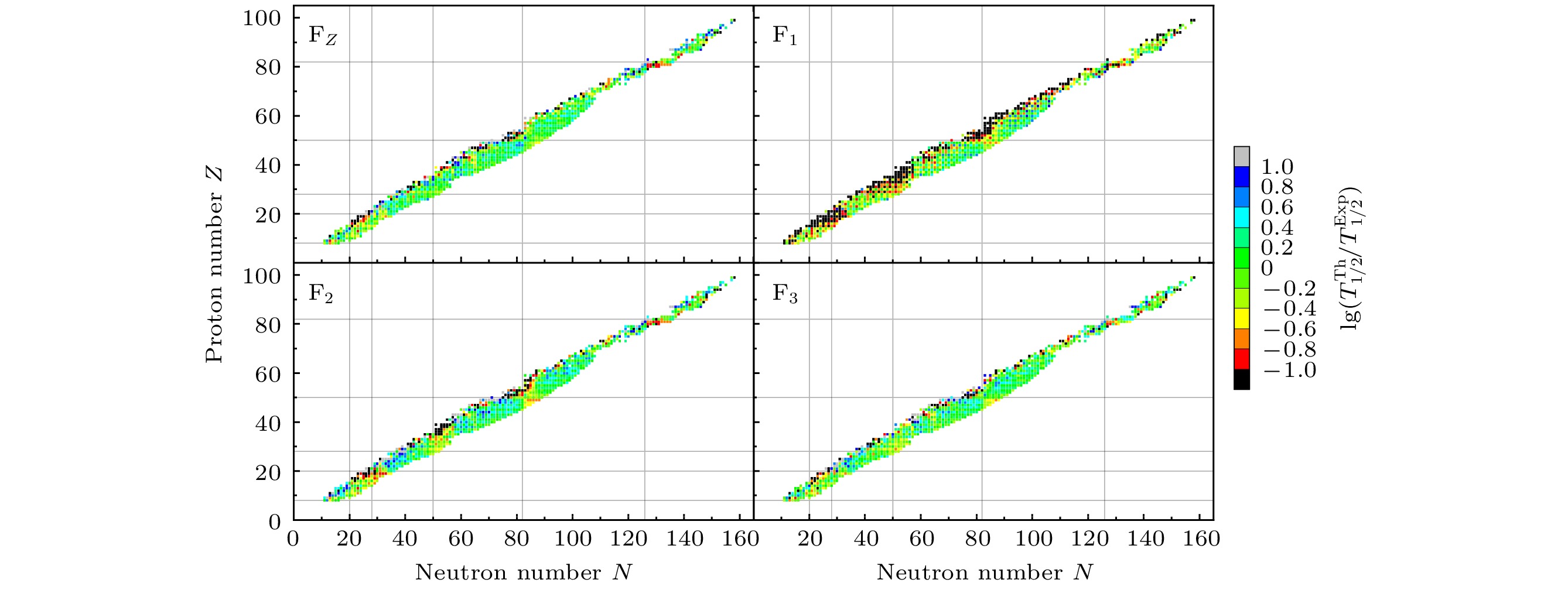
图 2 经验公式${\rm F}_1$, ${\rm F}_2$, ${\rm F}_3$, ${\rm F}_Z$的预测结果与实验数据的对数差随质子数Z和中子数N的变化. 竖线对应质子幻数$ Z=8, $$ 20, 28, 50, 82 $和中子幻数$ N=8, 20, 28, 50, 82, 126 $
Figure 2. Logarithmic differences between the predictions by the empirical formulas ${\rm F}_1$, ${\rm F}_2$, ${\rm F}_3$, ${\rm F}_Z$ and the experimental data as the functions of proton number Z and neutron number N. The vertical lines correspond to the proton magic numbers $ Z=8, 20, 28, 50, 82 $ and the neutron magic numbers $ N=8, 20, 28, 50, 82, 126 $
图 3 经验公式${\rm F}_1$, ${\rm F}_2$, ${\rm F}_3$, ${\rm F}_Z$的预测结果与实验数据的对数差
Figure 3. Logarithmic differences between the predictions by the empirical formulas ${\rm F}_1$, ${\rm F}_2$, ${\rm F}_3$, ${\rm F}_Z$ and the experimental data
图 4 ${\rm F}_1$, ${\rm F}_2$, ${\rm F}_3$预测的Ni, Sn, Pb同位素的$\beta$衰变寿命, 及其与${\rm F}_Z$计算结果的比较
Figure 4. Nuclear $\beta$-decay half-lives of Ni, Sn and Pb isotopes predicted by the ${\rm F}_1$, ${\rm F}_2$ and ${\rm F}_3$, and their comparison with ${\rm F}_Z$ calculations
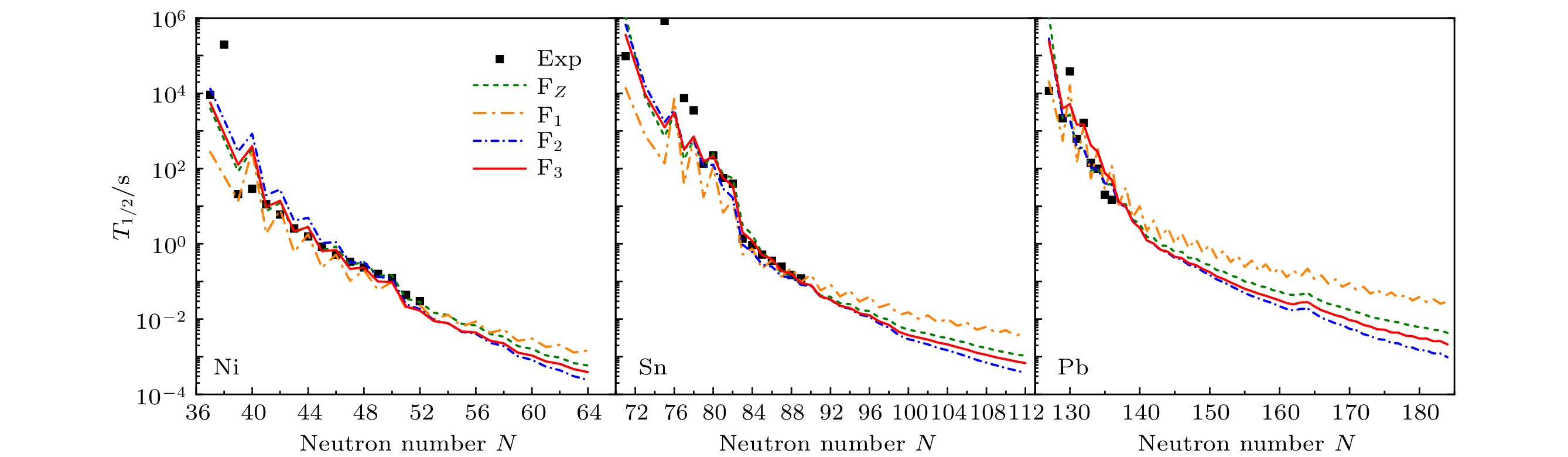
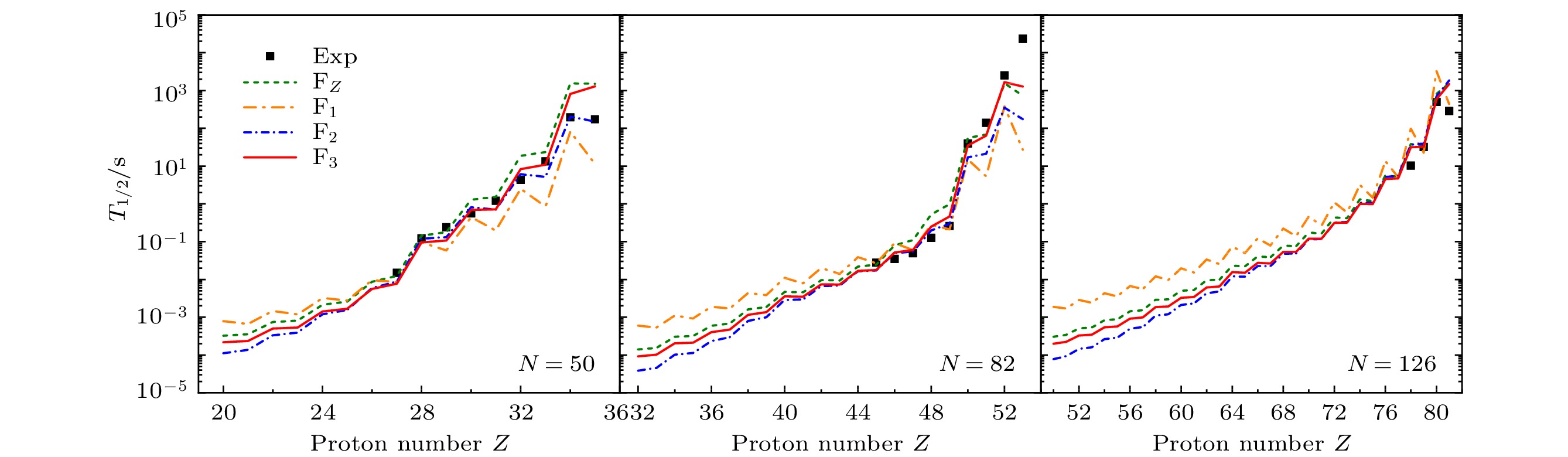
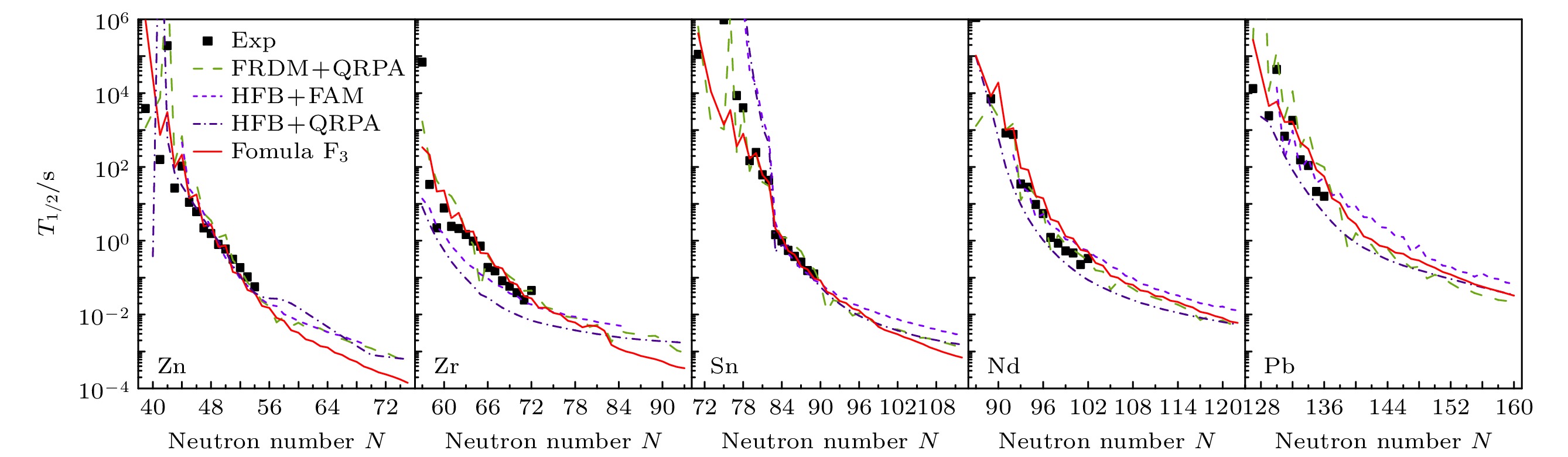
图 6 公式${\rm F}_3$预测的Zn, Zr, Sn, Nd, Pb同位素的$\beta$衰变寿命, 及其与FRDM + QRPA, HFB + FAM, HFB + QRPA理论结果的比较
Figure 6. Nuclear $\beta$-decay half-lives of Zn, Zr, Sn, Nd and Pb isotopes predicted by formula ${\rm F}_3$, and the comparison with the theoretical results of FRDM + QRPA, HFB + FAM and HFB + QRPA models
图 7 公式${\rm F}_3$预言的原子核$\beta$衰变寿命
Figure 7. Nuclear $\beta$-decay half-lives predicted by formula ${\rm F}_3$
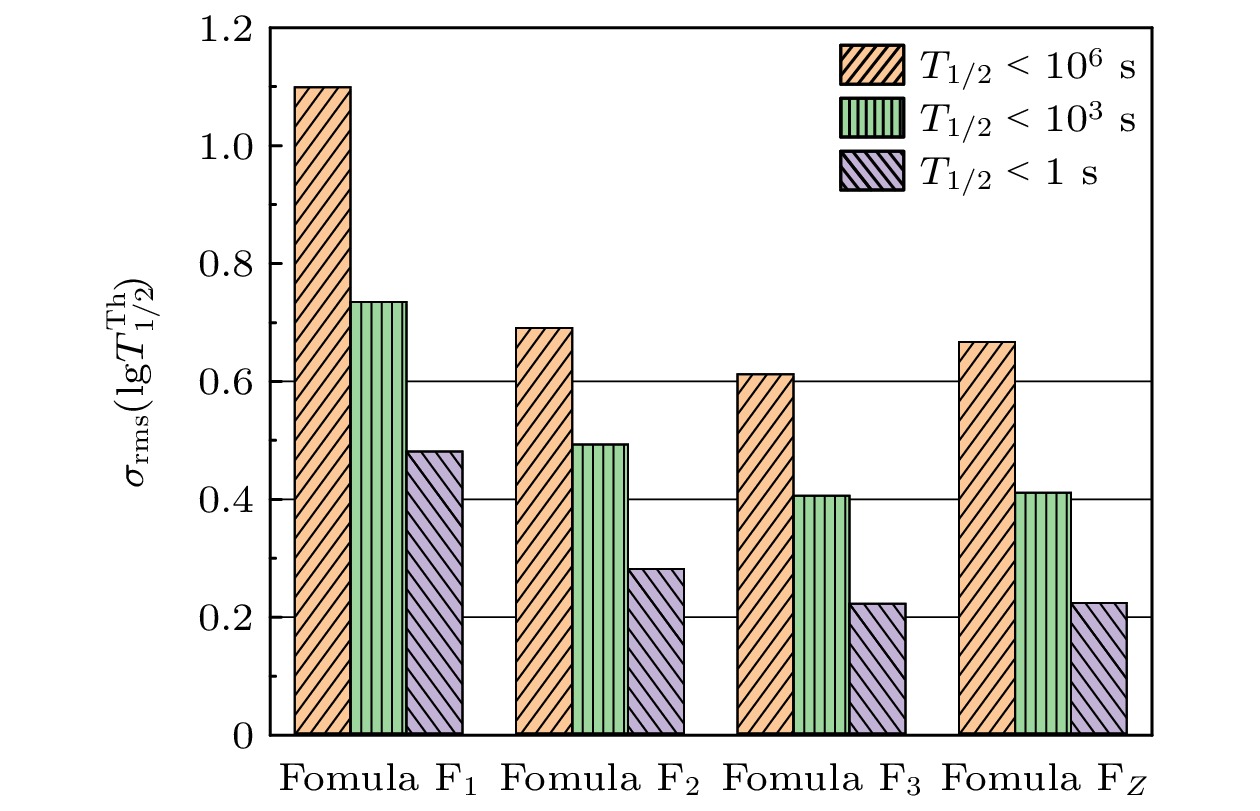
表 1 经验公式${\rm F}_1$, ${\rm F}_2$, ${\rm F}_3$和${\rm F}_Z$预言的原子核衰变寿命的对数与实验数据的均方根偏差$\sigma_{\rm{rms}}(\lg T_{1/2})$, 其中第2—4列分别对应$T_{1/2}< 10^6\ {\rm{s}}$, $T_{1/2}< 10^3\ {\rm{s}}$和$T_{1/2}< 1\ {\rm{s}}$的原子核数据集
Table 1. The rms deviations $\sigma_{\rm{rms}}(\lg T_{1/2})$ of the logarithms of nuclear $\beta$-decay half-lives predicted by the empirical formulas ${\rm F}_1$, ${\rm F}_2$, ${\rm F}_3$, and ${\rm F}_Z$ with respective to the experimental data, where the 2nd–4th columns represent the data sets for nuclei with $T_{1/2}< 10^6\ {\rm{s}}$, $T_{1/2}< 10^3\ {\rm{s}}$, and $T_{1/2}< 1\ {\rm{s}}$, respectively
Formula $ T_{1/2}< {10^6 \; {\rm{s}}}$ $T_{1/2}< {10^3 \; {\rm{s}}}$ $T_{1/2}< {1 \; {\rm{s}}}$ ${\rm F}_1$ 1.096 0.732 0.478 ${\rm F}_2$ 0.688 0.490 0.279 ${\rm F}_3$ 0.609 0.403 0.220 ${\rm F}_Z$ 0.664 0.408 0.221 
DownLoad: CSV
-
[1] Burbidge E M, Burbidge G R, Fowler W A, Hoyle F 1957 Rev. Mod. Phys. 29 547
Google Scholar
[2] Thielemann F K, Arcones A, Käappeli R, Liebendrfer M, Rauscher T, Winteler C, Fröhlichb C, Dillmannc I, Fischer T, Martinez-Pinedoc G, Langanke K, Farouqi K, Kratz K L, Panov I, Korneev I K 2011 Prog. Part. Nucl. Phys. 66 346
Google Scholar
[3] Cowan J J, Thielemann F K, Truran J W 1991 Phys. Rep. 208 267
Google Scholar
[4] Qian Y Z 2003 Prog. Part. Nucl. Phys. 50 153
Google Scholar
[5] Arnould M, Goriely S, Takahashi K 2007 Phys. Rep. 450 97
Google Scholar
[6] Chen J, Fang J Y, Hao Y W, Niu Z M, Niu Y F 2023 Astrophys. J. 943 102
Google Scholar
[7] Mumpower M R, Surmana R, McLaughlin G C, Aprahamian A 2016 Prog. Part. Nucl. Phys. 86 86
Google Scholar
[8] Li Z, Niu Z M, Sun B H 2019 Sci. China. Phys. Mech. Astron. 62 982011
Google Scholar
[9] Niu Z, Sun B, Meng J 2009 Phys. Rev. C 80 065806
Google Scholar
[10] Surman R, Engel J, Bennett J R, Meyer B S 1997 Phys. Rev. Lett. 79 1809
Google Scholar
[11] Zhang X P, Ren Z Z 2006 Phys. Rev. C 73 014305
Google Scholar
[12] Zhang X P, Ren Z Z, Zhi Q J, Zheng Q 2007 J. Phys. G: Nucl. Part. Phys. 34 2611
Google Scholar
[13] Zhou Y, Li Z H, Wang Y B, Chen Y S, Guo B, Su J, Li Y J, Yan S Q, Li X Y, Han Z Y, Shen Y P, Gan L, Zeng S, Lian G, Liu W P 2017 Sci. China-Phys. Mech. Astron. 60 082012
Google Scholar
[14] Takahashi K, Yamada M 1969 Prog. Theor. Phys. 41 1470
Google Scholar
[15] Tachibana T, Yamada M, Yoshida Y 1990 Prog. Theor. Phys. 84 641
Google Scholar
[16] Nakata H, Tachibana T, Yamada M 1997 Nucl. Phys. A 625 521
Google Scholar
[17] Koura H, Chiba S 2017 Phys. Rev. C 95 064304
Google Scholar
[18] Engel J, Bender M, Dobaczewski J, Surman R 1999 Phys. Rev. C 60 014302
Google Scholar
[19] Minato F, Bai C L 2013 Phys. Rev. Lett. 110 122501
Google Scholar
[20] Niu Z M, Niu Y F, Liang H Z, Long W H, Nikšić T, Vretenar D, Meng J 2013 Phys. Lett. B 723 172
Google Scholar
[21] Borzov I N, Goriely S 2000 Phys. Rev. C 62 035501
Google Scholar
[22] Langanke K, Martínez-Pinedo G 2003 Rev. Mod. Phys. 75 819
Google Scholar
[23] Martínez-Pinedo G, Langanke K 1999 Phys. Rev. Lett. 83 4502
Google Scholar
[24] Suzuki T, Yoshida T, Kajino T, Otsuka T 2012 Phys. Rev. C 85 015802
Google Scholar
[25] Zhi Q, Caurier E, Cuenca-García J J, Langanke K, Martínez-Pinedo G, Sieja K 2013 Phys. Rev. C 87 025803
Google Scholar
[26] Möller P, Pfeiffer B, Kratz K L 2003 Phys. Rev. C 67 055802
Google Scholar
[27] Minato F, Niu Z, Liang H 2022 Phys. Rev. C 106 024306
Google Scholar
[28] Marketin T, Huther L, Martinez-Pinedo G 2016 Phys. Rev. C 93 025805
Google Scholar
[29] Niu Z M, Niu Y F, Liu Q, Liang H Z, Guo J Y 2013 Phys. Rev. C 87 051303
Google Scholar
[30] Wang Z Y, Niu Y F, Niu Z M, Guo J Y 2016 J. Phys. G: Nucl. Part. Phys. 43 045108
Google Scholar
[31] Nakatsukasa T, Inakura T, Yabana K 2007 Phys. Rev. C 76 024318
Google Scholar
[32] Liang H Z, Nakatsukasa T, Niu Z M, Meng J 2013 Phys. Rev. C 87 054310
Google Scholar
[33] Ney E M, Engel J, Li T, Schunck N 2020 Phys. Rev. C 102 034326
Google Scholar
[34] Mustonen M T, Engel J 2016 Phys. Rev. C 93 014304
Google Scholar
[35] Endo F, Koura H 2019 Phys. Rev. C 99 034303
Google Scholar
[36] Fang J Y, Chen J, Niu Z M 2022 Phys. Rev. C 106 054318
Google Scholar
[37] Sargent B W 1933 Proc. R. Soc. Lond. A 139 659
Google Scholar
[38] Shi M, Fang J Y, Niu Z M 2021 Chin. Phys. C 45 044103
Google Scholar
[39] Uyen N K, Chae K Y, Duy N N, Ly N D 2022 J. Phys. G: Nucl. Part. Phys. 49 025201
Google Scholar
[40] Kondev F G, Wang M, Huang W J, Naimi S, Audi G 2021 Chin. Phys. C 45 030001
Google Scholar
[41] Fermi E 1934 Z. Phys. 88 161
Google Scholar
[42] Wang N, Liu M, Wu X, Meng J 2014 Phys. Lett. B 734 215
Google Scholar
[43] Möller P, Mumpower M R, Kawano T, Myers W D 2019 At. Data Nucl. Data Tables 125 1
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2239
- PDF Downloads: 71
- Cited By: 0
