-
Tunneling ionization of atoms is the basis of many phenomena and techniques, which requires people to be able to comprehensively understand this crucial physical process. Recent experiments have demonstrated the existence of the nonzero initial longitudinal momentum spread at the tunnel exit. However, the initial longitudinal velocity is usually set to be zero in the adiabatic regime. In this work, we numerically study that the initial longitudinal velocity of ionized-out electrons plays the role in the spiderlike photoelectron momentum distributions in hydrogen atom by using the semiclassical rescattering model and the time-dependent Schrödinger equation. Nonzero longitudinal initial velocity, no matter whether it is an offset or an offset distribution, is considered in the semiclassical rescattering model. Longitudinal cut-plot and transverse cut-plot of the photoelectron momentum distribution are discussed. The final longitudinal momentum of the electron is found to be sensitive to the initial longitudinal velocity, which offers us a method of determining the information about the initial longitudinal velocity from a photoelectron momentum distribution according to this linear relationship. We unveil that either an offset or an offset distribution for the initial longitudinal velocity can perfectly reproduce the same spiderlike photoelectron momentum distributions. The semiclassical results are backed by the full quantum simulation. It is expected that more precise research is required to deepen the knowledge of the initial longitudinal velocity in strong field ionization of atoms.
-
Keywords:
- semiclassical rescattering model /
- photoelectron momentum distributions /
- initial longitudinal velocity /
- spiderlike structure
[1] Krausz F, Ivanov M 2009 Rev. Mod. Phys. 81 163
Google Scholar
[2] Lewenstein M, Balcou Ph, Ivanov M Yu, L’Huillier Anne, Corkum P B 1994 Phys. Rev. A 49 2117
Google Scholar
[3] Corkum P B, Krausz F 2007 Nat. Phys. 3 381
Google Scholar
[4] Ye D, Li M, Fu L, Liu J, Gong Q, Liu Y, Ullrich J 2015 Phys. Rev. Lett. 115 123001
Google Scholar
[5] Wolter B, Pullen M G, Le A, Baudisch M, Doblhoff-Dier K, Senftleben A, Hemmer M, Schröter C D, Ullrich J, Pfeifer T, Moshammer R, Gräfe S, Vendrell O, Lin C D, Biegert J 2016 Science 354 308
Google Scholar
[6] Eckle P, Pfeiffer A N, Cirelli C, Staudte A, Dörner R, Muller H G, Büttiker M, Keller U 2008 Science 322 1525
Google Scholar
[7] Pfeiffer A N, Cirelli C, Smolarski M, Dimitrovski D, Abu-samha M, Madsen L B, Keller U 2012 Nat. Phys. 8 76
[8] Li M, Geng J, Liu H, Deng Y, Wu C, Peng L, Gong Q, Liu Y 2014 Phys. Rev. Lett. 112 113002
Google Scholar
[9] Li M, Geng J, Han M, Liu M, Peng L, Gong Q, Liu Y 2016 Phys. Rev. A 93 013402
Google Scholar
[10] Xia Q, Tao J, Cai J, Fu L, Liu J 2018 Phys. Rev. Lett. 121 143201
Google Scholar
[11] Pfeiffer A N, Cirelli C, Landsman A S, Smolarski M, Dimitrovski D, Madsen L B, Keller U 2012 Phys. Rev. Lett. 109 083002
Google Scholar
[12] Hofmann C, Landsman A S, Cirelli C, Pfeiffer A N, Keller U 2013 J. Phys. B: At. Mol. Opt. Phys. 46 125601
Google Scholar
[13] Han M, Li M, Liu M, Liu Y 2017 Phys. Rev. A 95 023406
Google Scholar
[14] Camus N, Yakaboylu E, Fechner L, Klaiber M, Laux M, Mi Y, Hatsagortsyan K Z, Pfeifer T, Keitel C H, Moshammer R 2017 Phys. Rev. Lett. 119 023201
Google Scholar
[15] Guo L, Chen S, Liu M, Shu Z, Hu S, Lu R, Han S, Chen J 2020 Phys. Rev. A 101 033415
Google Scholar
[16] Kelvich S A, Becker W, Goreslavski S P 2016 Phys. Rev. A 93 033411
Google Scholar
[17] Sun X, Li M, Yu J, Deng Y, Gong Q, Liu Y 2014 Phys. Rev. A 89 045402
Google Scholar
[18] Hofmann C, Landsman S, Zielinski A, Cirelli C, Zimmermann T, Scrinzi A, Keller U 2014 Phys. Rev. A 90 043406
Google Scholar
[19] Li M, Liu Y, Liu H, Ning Q, Fu L, Liu J, Deng Y, Wu C, Peng L, Gong Q 2013 Phys. Rev. L 111 023006
Google Scholar
[20] Hao X, Li W 2011 Phys. Rev. A 83 053422
Google Scholar
[21] Wu J, Meckel M, Voss S, Sann H, Kunitski M, Schmidt L Ph H, Czasch A, Kim H, Jahnke T, Dorner R 2012 Phys. Rev. Lett. 108 043002
Google Scholar
[22] Xu R, Li T, Wang X 2018 Phys. Rev. A 98 053435
Google Scholar
[23] Li M, Liu M, Geng J, Han M, Sun X, Shao Y, Deng Y, Wu C, Peng L, Gong Q, Liu Y 2017 Phys. Rev. A 95 053425
Google Scholar
[24] Luo S, Li M, Xie W, Liu K, Feng Y, Du B, Zhou Y, Lu P 2019 Phys. Rev. A 99 053422
Google Scholar
[25] Li M, Xie H, Cao W, Luo S, Tan J, Feng Y, Du B, Zhang W, Li Y, Zhang Q, Lan P, Zhou Y, Lu P 2019 Phys. Rev. Lett. 122 183202
Google Scholar
[26] Huismans Y, Rouzée A, Gijsbertsen A, Jungmann J H, Smolkowska A S, Logman P S W M, Lépine F, Cauchy C, Zamith S, Marchenko T, Bakker J M, Berden G, Redlich B, van der Meer A F G, Muller H G, Vermin W, Schafer K J, Spanner M, Ivanov M Yu, Smirnova O, Bauer D, Popruzhenko S V, Vrakking M J J 2011 Science 331 61
Google Scholar
[27] 唐久, 张贵忠, 何宇飞, 付国跃, 史伟, 姚建铨 2021 光学学报 41 1002001
Google Scholar
Tang J, Zhang G Z, He Y F, Fu G Y, Shi W, Yao J Q 2021 Acta Opt. Sin. 41 1002001
Google Scholar
[28] Paulus G G, Becker W, Nicklich W, Walther H 1994 J. Phys. B 27 L703
Google Scholar
[29] Bian X, Huismans Y, Smirnova O, Yuan K J, Vrakking M J J, Bandrauk A D 2011 Phys. Rev. A 84 043420
Google Scholar
[30] Xie H, Li M, Li Y, Zhou Y, Lu P 2016 Opt. Express 24 27726
Google Scholar
[31] Li M, Jiang W C, Xie H, Luo S, Zhou Y, Lu P 2018 Phys. Rev. A 97 023415
Google Scholar
[32] Brennecke S, Eicke N, Lein M 2020 Phys. Rev. Lett. 124 153202
Google Scholar
[33] Chelkowski S, Foisy C, Bandrauk A D 1998 Phys. Rev. A 57 1176
Google Scholar
-
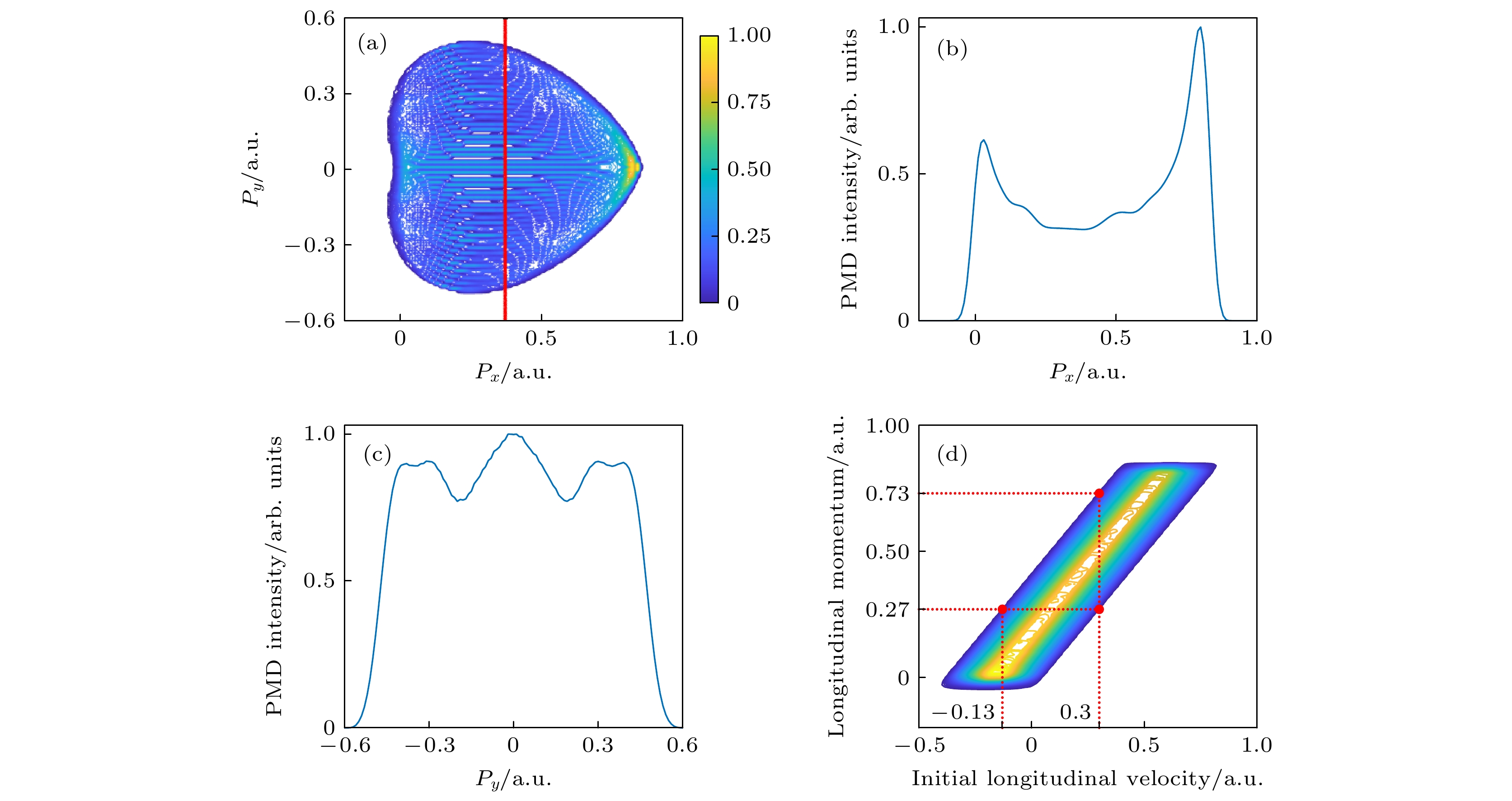
图 1 (a)—(c) 使用SRM模型得到的氢原子PMDs. 电子初速度取为常数, 分别是(a) 0 a.u., (b) 0.2 a.u.和 (c) 0.4 a.u., 其中彩色竖线标注了之后对动量谱作横向切割的动量位置, 归一化的色度条衡量动量谱的强度, 后文中的色度条同理. (d) 图1(a)—(c)中动量谱的纵向动量分布; (e) 纵向动量分布的左边界(红实线)、右边界(红虚线)和动量分布的宽度(蓝)随纵向初速度变化的曲线图. (f) 图1(a)—(c)中动量谱的横向动量分布; (g) 横向动量分布的第一(红)和第二(蓝)干涉极小位置随纵向初速度变化的曲线图. 图1(d)和图1(f)中红色、绿色和蓝色曲线分别与图1(a)—(c)相对应, 后文的横向和纵向动量分布曲线亦如是标记
Figure 1. (a)–(c) Spiderlike PMDs of hydrogen atom simulated by SRM for nonzero offset and zero distribution. The initial velocity is (a) 0 a.u., (b) 0.2 a.u., and (c) 0.4 a.u., respectively. The vertical lines in the figures interpret the longitudinal momentum positions for the transverse cut-plot curves (see below), and the normalized colorbar represents the intensity of the PMD. (d) Longitudinal cut-plot curves taken at py = 0 a.u.; (e) the left boundary momentum (red solid line), the right boundary momentum (red dash-dotted line) and the width or span of the longitudinal momentum distributions (blue). (f) Transverse cut-plot curves. The red and blue arrows mark the first and second interference minima; (g) the transverse momentum positions of the first and second interference minima as a function of the initial velocity. The red, green and blue curves in the figures correspond to Fig.1 (a), Fig.1 (b) and Fig.1 (c), and the same is true of the following PMDs.
图 2 (a)—(c)使用SRM模型得到的PMDs. 电子初速度取为分布, 分别是(a) 0—0.2 a.u., (b) 0.2—0.4 a.u., (c) 0.4—0.6 a.u.; (d) 图2(a)—(c)中动量谱的纵向动量分布; (e) 图2(a)—(c)中动量谱的横向动量分布
Figure 2. (a)–(c) Spiderlike PMDs simulated by SRM for nonzero offset and nonzero distribution. The initial velocity ranges are (a) 0 to 0.2 a.u., (b) 0.2 to 0.4 a.u., and (c) 0.4 to 0.6 a.u., respectively. (d) Longitudinal cut-plot curves; (e) transverse cut-plot curves.
图 3 使用SRM模型得到的PMDs (a) 电子初速度为–0.5—1 a.u.的光电子动量谱; (b) 图3(a)中动量谱的纵向动量分布; (c) 图3(a)中动量谱的横向动量分布; (d) 图3(a)中动量谱的纵向初速度与最终纵向动量之间的变化关系
Figure 3. Spiderlike PMDs simulated by SRM: (a) PMDs with wider initial velocity range of –0.5 to 1.0 a.u.; (b) longitudinal cut-plot curve; (c) transverse cut-plot curve; (d) the relationship between the final longitudinal momentum and the initial longitudinal velocity
图 4 变化激光脉冲强度时, 使用SRM模型得到的PMDs (a)—(c) 激光强度增大时, 对应的PMDs; (d) 图4(a)—(c)中动量谱的纵向动量分布; (e) 图4(a)—(c)中动量谱的横向动量分布; (f) 纵向动量分布的左边界(红实线)、右边界(红虚线)和动量分布的宽度(蓝)随纵向初速度变化的曲线图; (g)—(i) 图4(a)—(c)中动量谱的纵向初速度与最终纵向动量之间的变化关系. 对应的激光脉冲强度分别为 (a), (g) 2 × 1013 W/cm2; (b), (h) 4 × 1013 W/cm2; (c), (i) 8 × 1013 W/cm2
Figure 4. Spiderlike PMDs simulated by SRM: (a)−(c) Spiderlike PMDs simulated by SRM with increasing laser intensities; (d) longitudinal cut-plot curves; (e) transverse cut-plot curves; (f) the left boundary momentum (red solid line), right boundary momentum (red dash-dotted line) and the width of the longitudinal momentum distributions (blue); (g)−(i) the relationship between the final longitudinal momentum and the initial longitudinal velocity. The laser intensity is: (a), (g) 2 × 1013 W/cm2; (b), (h) 4 × 1013 W/cm2; (c), (i) 8 × 1013 W/cm2.
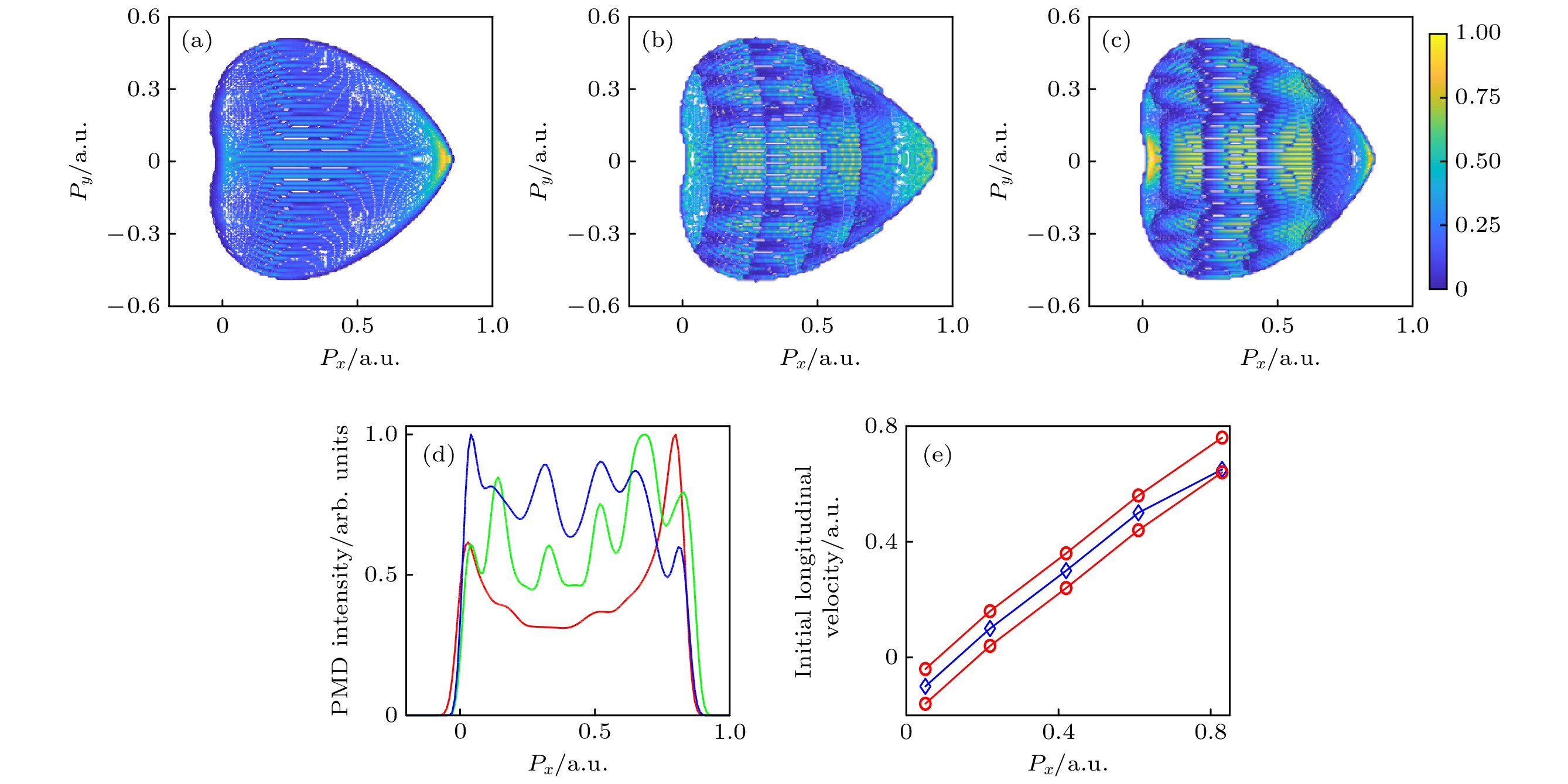
图 5 使用有多个常数或多段分布的初速度的SRM模型重建完整的PMDs (a) 取电子初速度为–0.5—1 a.u., 使用SRM模型得到的完整PMDs; (b) 取电子初速度为多个不同的常数值, 使用SRM模型得到的PMDs; (c) 取电子初速度为多段不同的分布, 使用SRM模型得到的PMDs; (d) 图5(a)—(c)中动量谱的纵向动量分布; (e) 模拟中取的电子初速度, 蓝色曲线对应图5(b), 红色曲线对应图5(c)
Figure 5. (a) Spiderlike PMDs simulated by SRM with initial velocity range of –0.5 to 1.0 a.u; (b) spiderlike PMD reconstructed by adding five PMDs each generated with a nonzero offset (no offset distribution); (c) spiderlike PMD reconstructed by adding five PMDs each generated with a nonzero offset distribution; (d) longitudinal cut-plot curves with the red, green and blue colors corresponding to Fig. 5(a)-(c); (e) the initial velocities of the five PMDs. The blue curve represents the initial velocities in Fig. 5(b), and the red curves represent the initial velocity ranges in Fig. 5(c).
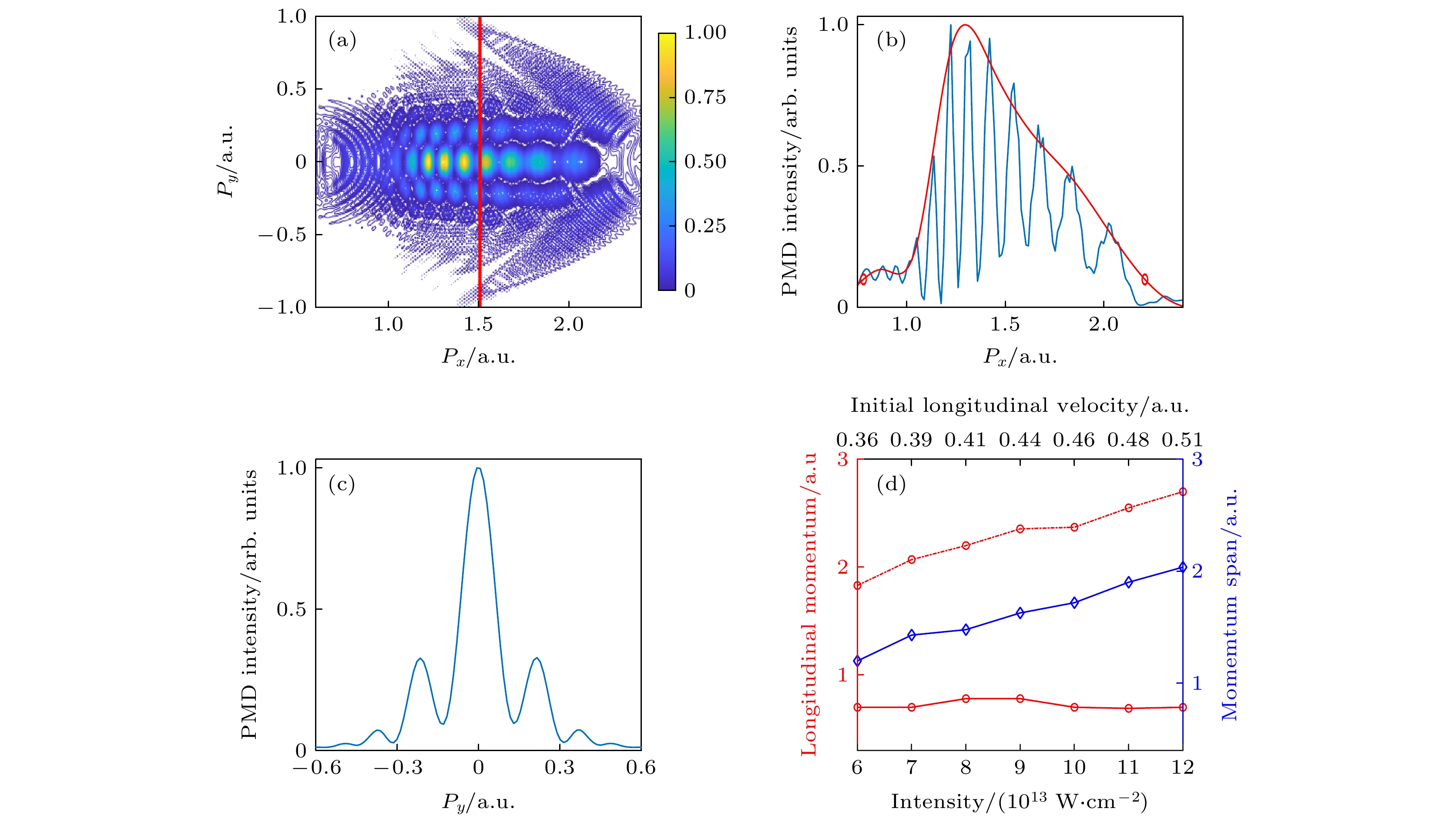
图 6 (a) 取激光脉冲强度为8 × 1013 W/cm2时, 数值求解TDSE得到的PMD; (b) 图6(a)中动量谱的纵向动量分布; (c) 图6(a)中动量谱的横向动量分布; (d) 纵向动量分布的左边界(红实线)、右边界(红虚线)和动量分布的宽度(蓝)随纵向初速度变化的曲线图
Figure 6. (a) Spiderlike PMD simulated by TDSE with laser pulse intensity of 8 × 1013 W/cm2; (b) longitudinal cut-plot curve; (c) transverse cut-plot curve; (d) the left boundary momentum (red solid line), right boundary momentum (red dash-dotted line) and the width or span of the longitudinal momentum distributions (blue) with respect to different laser intensities or initial velocities
-
[1] Krausz F, Ivanov M 2009 Rev. Mod. Phys. 81 163
Google Scholar
[2] Lewenstein M, Balcou Ph, Ivanov M Yu, L’Huillier Anne, Corkum P B 1994 Phys. Rev. A 49 2117
Google Scholar
[3] Corkum P B, Krausz F 2007 Nat. Phys. 3 381
Google Scholar
[4] Ye D, Li M, Fu L, Liu J, Gong Q, Liu Y, Ullrich J 2015 Phys. Rev. Lett. 115 123001
Google Scholar
[5] Wolter B, Pullen M G, Le A, Baudisch M, Doblhoff-Dier K, Senftleben A, Hemmer M, Schröter C D, Ullrich J, Pfeifer T, Moshammer R, Gräfe S, Vendrell O, Lin C D, Biegert J 2016 Science 354 308
Google Scholar
[6] Eckle P, Pfeiffer A N, Cirelli C, Staudte A, Dörner R, Muller H G, Büttiker M, Keller U 2008 Science 322 1525
Google Scholar
[7] Pfeiffer A N, Cirelli C, Smolarski M, Dimitrovski D, Abu-samha M, Madsen L B, Keller U 2012 Nat. Phys. 8 76
[8] Li M, Geng J, Liu H, Deng Y, Wu C, Peng L, Gong Q, Liu Y 2014 Phys. Rev. Lett. 112 113002
Google Scholar
[9] Li M, Geng J, Han M, Liu M, Peng L, Gong Q, Liu Y 2016 Phys. Rev. A 93 013402
Google Scholar
[10] Xia Q, Tao J, Cai J, Fu L, Liu J 2018 Phys. Rev. Lett. 121 143201
Google Scholar
[11] Pfeiffer A N, Cirelli C, Landsman A S, Smolarski M, Dimitrovski D, Madsen L B, Keller U 2012 Phys. Rev. Lett. 109 083002
Google Scholar
[12] Hofmann C, Landsman A S, Cirelli C, Pfeiffer A N, Keller U 2013 J. Phys. B: At. Mol. Opt. Phys. 46 125601
Google Scholar
[13] Han M, Li M, Liu M, Liu Y 2017 Phys. Rev. A 95 023406
Google Scholar
[14] Camus N, Yakaboylu E, Fechner L, Klaiber M, Laux M, Mi Y, Hatsagortsyan K Z, Pfeifer T, Keitel C H, Moshammer R 2017 Phys. Rev. Lett. 119 023201
Google Scholar
[15] Guo L, Chen S, Liu M, Shu Z, Hu S, Lu R, Han S, Chen J 2020 Phys. Rev. A 101 033415
Google Scholar
[16] Kelvich S A, Becker W, Goreslavski S P 2016 Phys. Rev. A 93 033411
Google Scholar
[17] Sun X, Li M, Yu J, Deng Y, Gong Q, Liu Y 2014 Phys. Rev. A 89 045402
Google Scholar
[18] Hofmann C, Landsman S, Zielinski A, Cirelli C, Zimmermann T, Scrinzi A, Keller U 2014 Phys. Rev. A 90 043406
Google Scholar
[19] Li M, Liu Y, Liu H, Ning Q, Fu L, Liu J, Deng Y, Wu C, Peng L, Gong Q 2013 Phys. Rev. L 111 023006
Google Scholar
[20] Hao X, Li W 2011 Phys. Rev. A 83 053422
Google Scholar
[21] Wu J, Meckel M, Voss S, Sann H, Kunitski M, Schmidt L Ph H, Czasch A, Kim H, Jahnke T, Dorner R 2012 Phys. Rev. Lett. 108 043002
Google Scholar
[22] Xu R, Li T, Wang X 2018 Phys. Rev. A 98 053435
Google Scholar
[23] Li M, Liu M, Geng J, Han M, Sun X, Shao Y, Deng Y, Wu C, Peng L, Gong Q, Liu Y 2017 Phys. Rev. A 95 053425
Google Scholar
[24] Luo S, Li M, Xie W, Liu K, Feng Y, Du B, Zhou Y, Lu P 2019 Phys. Rev. A 99 053422
Google Scholar
[25] Li M, Xie H, Cao W, Luo S, Tan J, Feng Y, Du B, Zhang W, Li Y, Zhang Q, Lan P, Zhou Y, Lu P 2019 Phys. Rev. Lett. 122 183202
Google Scholar
[26] Huismans Y, Rouzée A, Gijsbertsen A, Jungmann J H, Smolkowska A S, Logman P S W M, Lépine F, Cauchy C, Zamith S, Marchenko T, Bakker J M, Berden G, Redlich B, van der Meer A F G, Muller H G, Vermin W, Schafer K J, Spanner M, Ivanov M Yu, Smirnova O, Bauer D, Popruzhenko S V, Vrakking M J J 2011 Science 331 61
Google Scholar
[27] 唐久, 张贵忠, 何宇飞, 付国跃, 史伟, 姚建铨 2021 光学学报 41 1002001
Google Scholar
Tang J, Zhang G Z, He Y F, Fu G Y, Shi W, Yao J Q 2021 Acta Opt. Sin. 41 1002001
Google Scholar
[28] Paulus G G, Becker W, Nicklich W, Walther H 1994 J. Phys. B 27 L703
Google Scholar
[29] Bian X, Huismans Y, Smirnova O, Yuan K J, Vrakking M J J, Bandrauk A D 2011 Phys. Rev. A 84 043420
Google Scholar
[30] Xie H, Li M, Li Y, Zhou Y, Lu P 2016 Opt. Express 24 27726
Google Scholar
[31] Li M, Jiang W C, Xie H, Luo S, Zhou Y, Lu P 2018 Phys. Rev. A 97 023415
Google Scholar
[32] Brennecke S, Eicke N, Lein M 2020 Phys. Rev. Lett. 124 153202
Google Scholar
[33] Chelkowski S, Foisy C, Bandrauk A D 1998 Phys. Rev. A 57 1176
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3285
- PDF Downloads: 65
- Cited By: 0
