Routing in spatial networks based on shortest path length

Lin Hong; Xia Yong-Xiang; Jiang Lu-Rong

doi:10.7498/aps.71.20211621

Abstract

In many complex networks, such as communication networks, power grids, and transportation networks, the main task is load transmission from sources to destinations. Therefore, the transmission throughput is a very important indicator to measure the network performance, and improving the throughput becomes one of the hotspots in the research of these complex networks. Many researchers have proposed different routing algorithms to improve the network throughput. However, few of them considered the spatial location of nodes in the network. Indeed, many real-world networks can be modeled by spatial networks, where the spatial location of nodes plays a vital role in determining the structure and dynamic behaviors of such networks. Specifically, when the locations of nodes are considered, each link has a length. And the shortest path may have different meaning. Traditionally, the shortest path indicates the path which passes the least number of links from source to destination, or the least number of hops. However, when the length of link is taken into account, the least number of links does not mean the least summation of link lengths along the path. The latter can be called the shortest path length. To this end, we proposes an efficient routing strategy for spatial networks based on the shortest path length in this work. In order to test the effectiveness of the algorithm, the network throughput ${R}_{\rm c}$ is used, at which the network changes from a free flow state to a congestion state, to measure the performance of the network. Simulations of homogeneous and heterogeneous spatial networks show that compared with the traditional least number of hops routing strategy, the routing algorithm based on the shortest path length proposed in this paper can effectively improve the throughput of the network. The routing algorithm proposed in this paper can be applied to many real-world spatial networks for improving their performances.

Keywords:

Authors and contacts

1.
School of Communication Engineering, Hangzhou Dianzi University, Hangzhou 310018, China
2.
School of Information Science and Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China

Corresponding author: Xia Yong-Xiang, xiayx@hdu.edu.cn

Funds: Project supported by the Open Fund of Laboratory of Science and Technology on Integrated Logistic Support of China and the National Natural Science Foundation of China (Grant No. 61602417)

FullText HTML : translate this paragraph

References

[1]	Erdös P, Rényi A 1959 Publ. Math. 6 290
[2]	Barabási A L, Albert R 1999 Science 286 509 Google Scholar
[3]	Watts D J, Strogatz S H 1998 Nature 393 440 Google Scholar
[4]	陈关荣 2008 力学进展 38 653 Google Scholar Chen G R 2008 Adv. Mech. 38 653 Google Scholar
[5]	马金龙, 张俊峰, 张冬雯, 张红斌 2021 70 078902 Google Scholar Ma J L, Zhang J F, Zhang D W, Zhang H B 2021 Acta Phys. Sin. 70 078902 Google Scholar
[6]	于晓 2020 软件工程 23 1 Google Scholar Yu X 2020 Software Engineering 23 1 Google Scholar
[7]	任卓明 2020 69 048901 Google Scholar Ren Z M 2020 Acta Phys. Sin. 69 048901 Google Scholar
[8]	Hearnshaw E J S, Wilson M M J 2013 Int. J. Operat. Product. Manage. 33 442 Google Scholar
[9]	Chen S Y, Huang W, Cattani C, Altieri G 2012 Math. Probl. Eng. 2012 732698 Google Scholar
[10]	Tan F, Wu J J, Xia Y X, Tse C K 2014 Phys. Rev. E 89 062813 Google Scholar
[11]	陈华良, 刘忠信, 陈增强, 袁著祉 2009 58 6068 Google Scholar Chen H L, Liu Z X, Chen Z Q, Yuan Z Z 2009 Acta Phys. Sin. 58 6068 Google Scholar
[12]	刘伟彦, 刘斌 2014 63 248901 Google Scholar Liu W Y, Liu B 2014 Acta Phys. Sin. 63 248901 Google Scholar
[13]	赵磊, 周金和 2019 计算机科学 46 137 Google Scholar Zhao L, Zhou J H 2019 Computer Science 46 137 Google Scholar
[14]	刘金良 2013 62 040503 Google Scholar Liu J L 2013 Acta Phys. Sin. 62 040503 Google Scholar
[15]	赵宇红 2019 博士学位论文 (北京: 北京科技大学) Zhao Y H 2019 Ph. D. Dissertation (Beijing: University of Science and Technology Beijing) (in Chinese)
[16]	李世宝, 娄琳琳, 陈瑞祥, 洪利 2014 63 028901 Google Scholar Li S B, Lou L L, Chen R X, Hong L 2014 Acta Phys. Sin. 63 028901 Google Scholar
[17]	邵斐, 蒋国平 2011 60 078902 Google Scholar Shao F, Jiang G P 2011 Acta Phys. Sin. 60 078902 Google Scholar
[18]	Yan G, Zhou T, Hu B, Fu Z Q, Wang B H 2005 Phys. Rev. E 73 046108 Google Scholar
[19]	Huang W, Chow T W S 2009 Chaos 19 043124 Google Scholar
[20]	Wang W X, Wang B H, Yin C Y, Xie Y B, Zhou T 2006 Phys. Rev. E 73 026111 Google Scholar
[21]	Xia Y X, Wang C, Shen H L, Song H N 2020 Physica A 559 125071 Google Scholar
[22]	Zhang M, Chen S, Sun L, Du W, Cao X 2021 Engineering 7 465 Google Scholar
[23]	Du W B, Zhou X L, Jusup M, Wang Z 2016 Sci. Rep. 6 19059 Google Scholar
[24]	Jiang L, Xu Q, Pan H, Dai Y, Tong J 2020 Secur. Commun. Netw. 2020 6513920 Google Scholar
[25]	Bai G H, Li Y J, Fang Y N, Zhang Y A, Tao J Y 2020 Reliab. Eng. Syst. Saf. 193 106602 Google Scholar
[26]	Zhao L, Lai Y C, Park K, Ye N 2005 Phys. Rev. E 71 026125 Google Scholar
[27]	Dall J, Christensen M 2002 Phys. Rev. E 66 016121 Google Scholar
[28]	Jiang L R, Jin X Y, Xia Y X, Ouyang B, Wu D P, Chen X 2015 Int. J. Distrib. Sens. Netw. 2014 764698 Google Scholar

Cited By

图 1 LAEE演化模型

Figure 1. LAEE evolution model.

DownLoad: Full-Size Img PowerPoint

图 2 N = 1500, $ \left\langle{k}\right\rangle $ = 8时的LAEE网络的度分布

Figure 2. Degree distribution of the LAEE network. N = 1500, $ \left\langle{k}\right\rangle $ = 8.

DownLoad: Full-Size Img PowerPoint

图 3 节点i与其连通区域内的全部节点建立连接

Figure 3. Node i connects all nodes in its connection area.

DownLoad: Full-Size Img PowerPoint

图 4 节点i与其连通范围内的节点以p概率进行连接

Figure 4. Node i connects nodes within its connection range with probability p.

DownLoad: Full-Size Img PowerPoint

图 5 N = 1500, $ \left\langle{k}\right\rangle $ = 8时改进的随机几何图的度分布

Figure 5. Degree distribution of the improved random geometric graph. N = 1500, $ \left\langle{k}\right\rangle $= 8.

DownLoad: Full-Size Img PowerPoint

图 6 平均度$ \left\langle{k}\right\rangle=4 $时, 不同节点规模下两种路由方式平均路径长度的比较　(a) LAEE演化模型; (b)改进的随机几何图模型. 图中每个点是10次仿真的平均值

Figure 6. With the average degree $ \left\langle{k}\right\rangle=4 $, the average path length under two routing strategies with different node sizes: (a) LAEE evolution model; (b) improved random geometric graph model. Each point is the average of 10 runs.

DownLoad: Full-Size Img PowerPoint

图 7 平均度$ \left\langle{k}\right\rangle=4 $时, 不同节点规模下两种路由方式平均跳数的比较　(a) LAEE演化模型; (b)改进的随机几何图模型. 图中每个点是10次仿真的平均值

Figure 7. With the average degree $ \left\langle{k}\right\rangle=4 $, the average number of hops under two routing strategies with different node sizes: (a) LAEE evolution model; (b) improved random geometric graph model. Each point is the average of 10 runs.

DownLoad: Full-Size Img PowerPoint

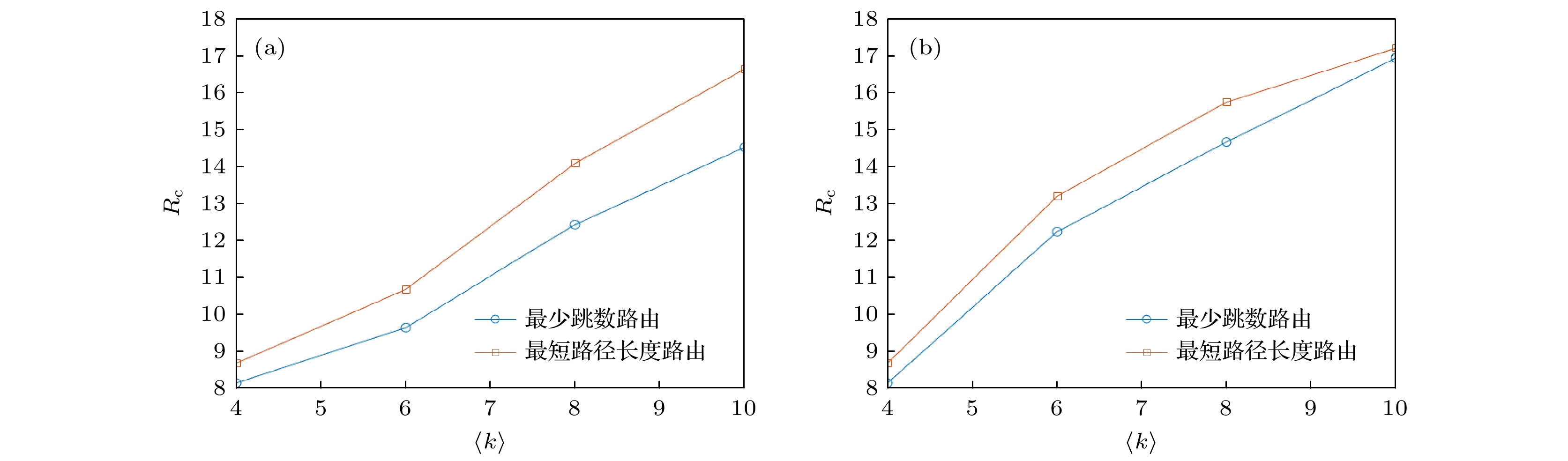
图 8 平均度$ \left\langle{k}\right\rangle=4 $时, 不同节点规模下两种路由方式的网络最大吞吐量$ {R}_{\rm{c}} $的比较　(a) LAEE演化模型; (b)改进的随机几何图模型. 图中每个点是10次仿真的平均值

Figure 8. With the average degree$\left\langle{k}\right\rangle=4$, $ {R}_{\rm{c}} $ under two routing strategies with different node sizes: (a) LAEE evolution model; (b) improved random geometric graph model. Each point is the average of 10 runs.

DownLoad: Full-Size Img PowerPoint

图 9 节点数$ N=1000 $时, 不同平均度下两种路由方式平均路径长度的比较　(a) LAEE演化模型; (b)改进的随机几何图模型. 图中每个点是10次仿真的平均值

Figure 9. With N = 1000, the average path length under two routing strategies with different average degrees: (a) LAEE evolution model; (b) improved random geometric graph model. Each point is the average of 10 runs.

DownLoad: Full-Size Img PowerPoint

图 10 节点数$ N=1000 $时, 不同平均度下两种路由方式平均跳数的比较　(a) LAEE演化模型; (b)改进的随机几何图模型. 图中每个点是10次仿真的平均值

Figure 10. With N = 1000, the average number of hops under two routing strategies with different average degrees: (a) LAEE evolution model; (b) improved random geometric graph model. Each point is the average of 10 runs.

DownLoad: Full-Size Img PowerPoint

图 11 节点数$ N=1000 $时, 不同平均度下两种路由方式的网络最大吞吐量$ {R}_{\rm{c}} $的比较　(a) LAEE演化模型; (b)改进的随机几何图模型. 图中每个点是10次仿真的平均值

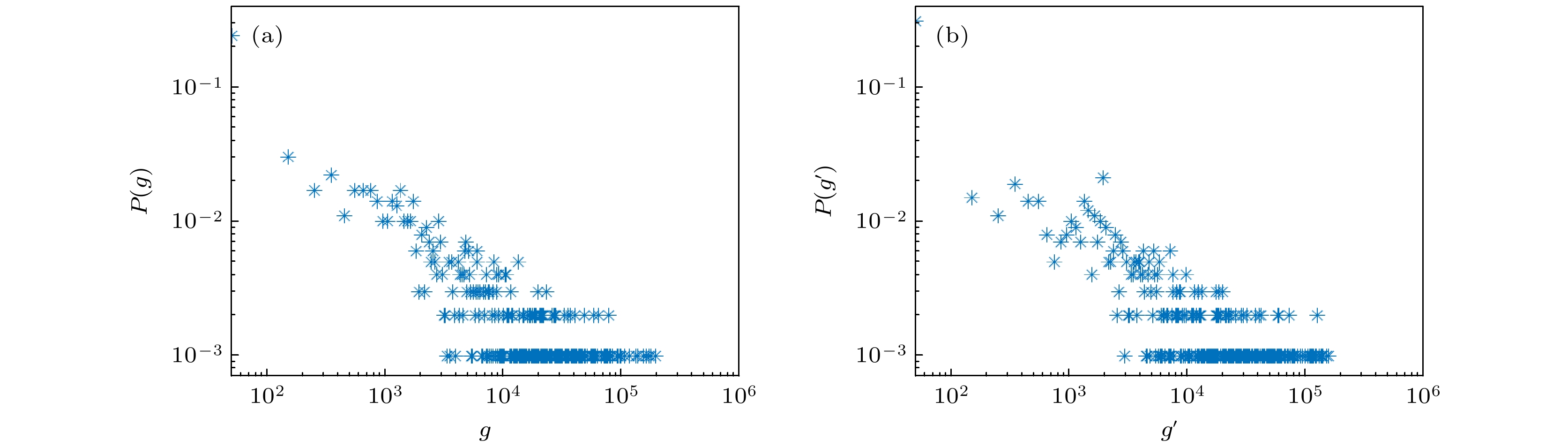
Figure 11. With $ N=1000 $, $ {R}_{c} $ under two routing strategies with different average degrees: (a) LAEE evolution model; (b) improved random geometric graph model. Each point is the average of 10 runs.

DownLoad: Full-Size Img PowerPoint

图 12 LAEE演化模型中, 节点数N = 1000, $ \left\langle{k}\right\rangle $= 4时的介数分布　(a)最少跳数路由; (b)最短路径长度路由

Figure 12. Betweenness distribution of the LAEE network with N = 1000, $ \left\langle{k}\right\rangle $ = 4: (a) Least number of hops routing strategy; (b) shortest path length routing strategy.

DownLoad: Full-Size Img PowerPoint

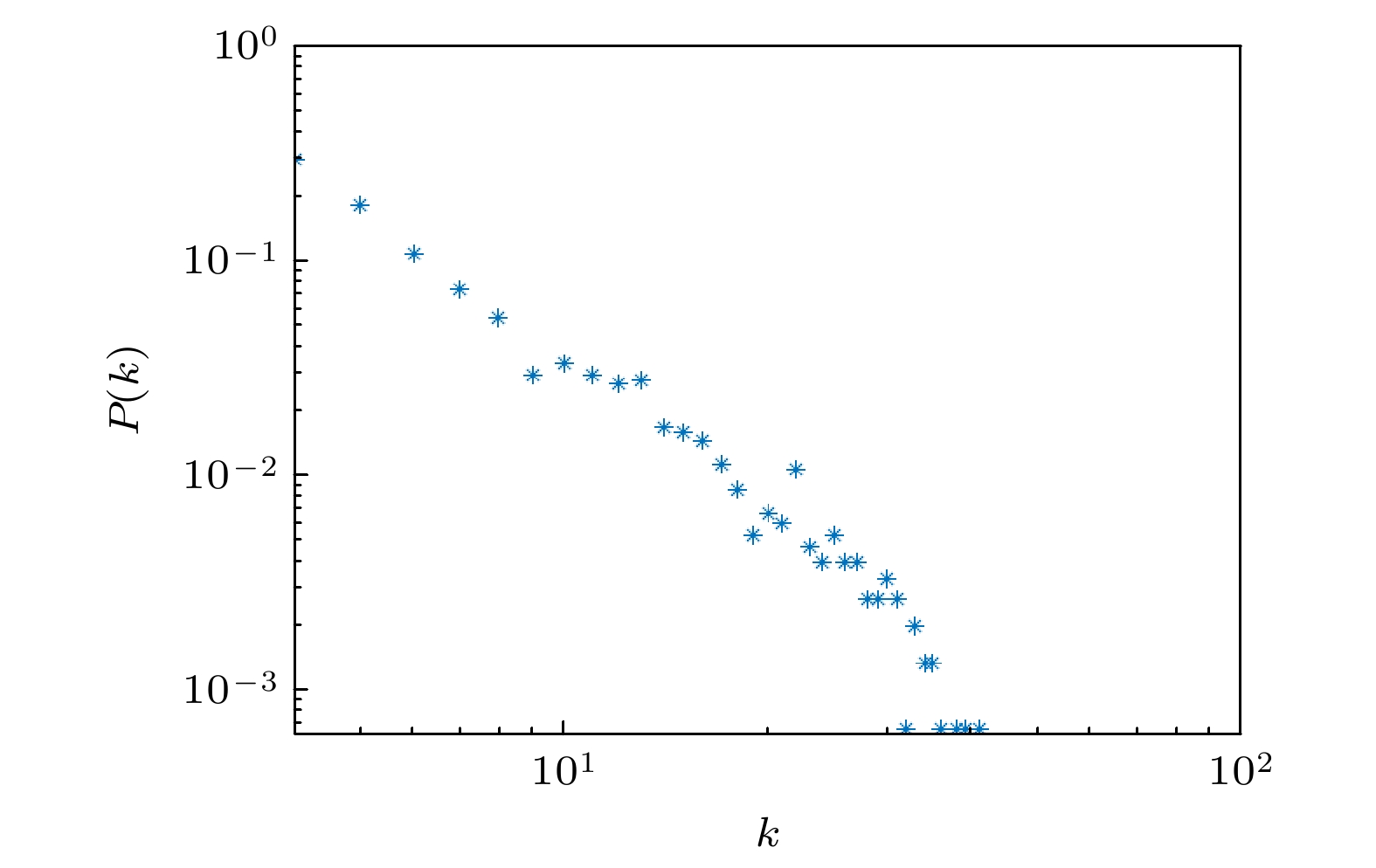
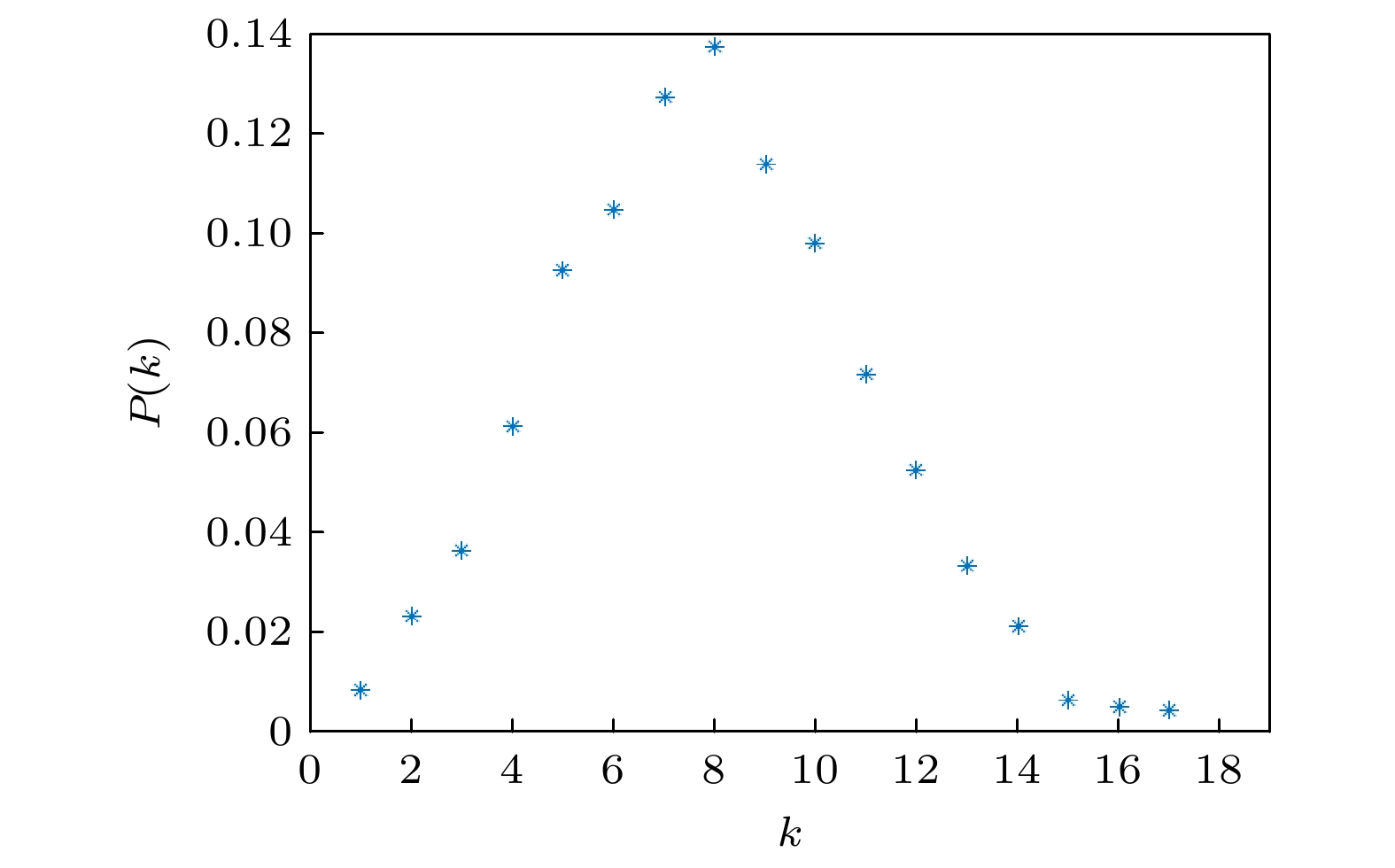
图 13 改进的随机几何图模型中, 节点数N = 1000, $ \left\langle{k}\right\rangle $ = 4时的介数分布　(a)最少跳数路由; (b)最短路径长度路由

Figure 13. Betweenness distribution of the improved random geometric graph with N = 1000, $ \left\langle{k}\right\rangle $ = 4: (a) Least number of hops routing strategy; (b) shortest path length routing strategy.

DownLoad: Full-Size Img PowerPoint

map

[1]	Erdös P, Rényi A 1959 Publ. Math. 6 290
[2]	Barabási A L, Albert R 1999 Science 286 509 Google Scholar
[3]	Watts D J, Strogatz S H 1998 Nature 393 440 Google Scholar
[4]	陈关荣 2008 力学进展 38 653 Google Scholar Chen G R 2008 Adv. Mech. 38 653 Google Scholar
[5]	马金龙, 张俊峰, 张冬雯, 张红斌 2021 70 078902 Google Scholar Ma J L, Zhang J F, Zhang D W, Zhang H B 2021 Acta Phys. Sin. 70 078902 Google Scholar
[6]	于晓 2020 软件工程 23 1 Google Scholar Yu X 2020 Software Engineering 23 1 Google Scholar
[7]	任卓明 2020 69 048901 Google Scholar Ren Z M 2020 Acta Phys. Sin. 69 048901 Google Scholar
[8]	Hearnshaw E J S, Wilson M M J 2013 Int. J. Operat. Product. Manage. 33 442 Google Scholar
[9]	Chen S Y, Huang W, Cattani C, Altieri G 2012 Math. Probl. Eng. 2012 732698 Google Scholar
[10]	Tan F, Wu J J, Xia Y X, Tse C K 2014 Phys. Rev. E 89 062813 Google Scholar
[11]	陈华良, 刘忠信, 陈增强, 袁著祉 2009 58 6068 Google Scholar Chen H L, Liu Z X, Chen Z Q, Yuan Z Z 2009 Acta Phys. Sin. 58 6068 Google Scholar
[12]	刘伟彦, 刘斌 2014 63 248901 Google Scholar Liu W Y, Liu B 2014 Acta Phys. Sin. 63 248901 Google Scholar
[13]	赵磊, 周金和 2019 计算机科学 46 137 Google Scholar Zhao L, Zhou J H 2019 Computer Science 46 137 Google Scholar
[14]	刘金良 2013 62 040503 Google Scholar Liu J L 2013 Acta Phys. Sin. 62 040503 Google Scholar
[15]	赵宇红 2019 博士学位论文 (北京: 北京科技大学) Zhao Y H 2019 Ph. D. Dissertation (Beijing: University of Science and Technology Beijing) (in Chinese)
[16]	李世宝, 娄琳琳, 陈瑞祥, 洪利 2014 63 028901 Google Scholar Li S B, Lou L L, Chen R X, Hong L 2014 Acta Phys. Sin. 63 028901 Google Scholar
[17]	邵斐, 蒋国平 2011 60 078902 Google Scholar Shao F, Jiang G P 2011 Acta Phys. Sin. 60 078902 Google Scholar
[18]	Yan G, Zhou T, Hu B, Fu Z Q, Wang B H 2005 Phys. Rev. E 73 046108 Google Scholar
[19]	Huang W, Chow T W S 2009 Chaos 19 043124 Google Scholar
[20]	Wang W X, Wang B H, Yin C Y, Xie Y B, Zhou T 2006 Phys. Rev. E 73 026111 Google Scholar
[21]	Xia Y X, Wang C, Shen H L, Song H N 2020 Physica A 559 125071 Google Scholar
[22]	Zhang M, Chen S, Sun L, Du W, Cao X 2021 Engineering 7 465 Google Scholar
[23]	Du W B, Zhou X L, Jusup M, Wang Z 2016 Sci. Rep. 6 19059 Google Scholar
[24]	Jiang L, Xu Q, Pan H, Dai Y, Tong J 2020 Secur. Commun. Netw. 2020 6513920 Google Scholar
[25]	Bai G H, Li Y J, Fang Y N, Zhang Y A, Tao J Y 2020 Reliab. Eng. Syst. Saf. 193 106602 Google Scholar
[26]	Zhao L, Lai Y C, Park K, Ye N 2005 Phys. Rev. E 71 026125 Google Scholar
[27]	Dall J, Christensen M 2002 Phys. Rev. E 66 016121 Google Scholar
[28]	Jiang L R, Jin X Y, Xia Y X, Ouyang B, Wu D P, Chen X 2015 Int. J. Distrib. Sens. Netw. 2014 764698 Google Scholar

[1]	Ma Jin-Long, Zhang Jun-Feng, Zhang Dong-Wen, Zhang Hong-Bin. Quantifying complex network traffic capacity based on communicability sequence entropy. Acta Physica Sinica, 2021, 70(7): 078902. doi: 10.7498/aps.70.20201300
[2]	Jiang Wen-Jun, Liu Run-Ran, Fan Tian-Long, Liu Shuang-Shuang, Lü Lin-Yuan. Overview of precaution and recovery strategies for cascading failures in multilayer networks. Acta Physica Sinica, 2020, 69(8): 088904. doi: 10.7498/aps.69.20192000
[3]	Nie Min, Liu Guang-Teng, Yang Guang, Pei Chang-Xing. Voice over quantum IP routing based on least relay node constrained optimization strategy. Acta Physica Sinica, 2016, 65(12): 120302. doi: 10.7498/aps.65.120302
[4]	Yang Xian-Xia, Pu Cun-Lai, Xu Zhong-Qi, Chen Rong-Bin, Wu Jie-Xin, Li Lun-Bo. Energy-based hybrid routing strategy for scale-free networks. Acta Physica Sinica, 2016, 65(24): 248901. doi: 10.7498/aps.65.248901
[5]	Liu Wei-Yan, Liu Bin. Congestion control in complex network based on local routing strategy. Acta Physica Sinica, 2014, 63(24): 248901. doi: 10.7498/aps.63.248901
[6]	Li Shi-Bao, Lou Lin-Lin, Chen Rui-Xiang, Hong Li. A pervasive optimized algorithm for complex network routing strategy. Acta Physica Sinica, 2014, 63(2): 028901. doi: 10.7498/aps.63.028901
[7]	Liu Xiao-Hui, Nie Min, Pei Chang-Xing. Quantum wireless wide-area networks and routing strategy. Acta Physica Sinica, 2013, 62(20): 200304. doi: 10.7498/aps.62.200304
[8]	Yu Xu-Tao, Xu Jin, Zhang Zai-Chen. Routing protocol for wireless ad hoc quantum communication network based on quantum teleportation. Acta Physica Sinica, 2012, 61(22): 220303. doi: 10.7498/aps.61.220303
[9]	Li Yong, Dou Fei-Ling, Fan Ying, Di Zeng-Ru. Theoretical analysis on optimal navigation with total energy restriction in a two-dimensional lattice. Acta Physica Sinica, 2012, 61(22): 228902. doi: 10.7498/aps.61.228902
[10]	Dou Fei-Ling, Hu Yan-Qing, Li Yong, Fan Ying, Di Zeng-Ru. Random walks on spatial networks. Acta Physica Sinica, 2012, 61(17): 178901. doi: 10.7498/aps.61.178901
[11]	Wang Dan, Jin Xiao-Zheng. On weightd scale-free network model with tunable clustering and congesstion. Acta Physica Sinica, 2012, 61(22): 228901. doi: 10.7498/aps.61.228901
[12]	Liu Gang, Li Yong-Shu. Study on the congestion phenomena in complex network based on gravity constraint. Acta Physica Sinica, 2012, 61(10): 108901. doi: 10.7498/aps.61.108901
[13]	Liu Gang, Li Yong-Shu. Routing strategy for complex networks based on gravitation field theory. Acta Physica Sinica, 2012, 61(24): 248901. doi: 10.7498/aps.61.248901
[14]	Zhou Xiao-Qing, Wu Yun-Wen, Zhao Han. Quantum teleportation internetworking and routing strategy. Acta Physica Sinica, 2011, 60(4): 040304. doi: 10.7498/aps.60.040304.2
[15]	Wang Kai, Zhou Si-Yuan, Zhang Yi-Feng, Pei Wen-Jiang, Liu Qian. A modified optimal routing strategy based on random walk on complex networks. Acta Physica Sinica, 2011, 60(11): 118903. doi: 10.7498/aps.60.118903
[16]	Pu Cun-Lai, Pei Wen-Jiang. A global routing method for weighted scale-free networks. Acta Physica Sinica, 2010, 59(6): 3841-3845. doi: 10.7498/aps.59.3841
[17]	Li Tao, Pei Wen-Jiang, Wang Shao-Ping. Optimal traffic routing strategy on scale-free complex networks. Acta Physica Sinica, 2009, 58(9): 5903-5910. doi: 10.7498/aps.58.5903
[18]	Qian Jiang-Hai, Han Ding-Ding. Gravity model for spatial network based on optimal expected traffic. Acta Physica Sinica, 2009, 58(5): 3028-3033. doi: 10.7498/aps.58.3028
[19]	Wang Dan, Yu Hao, Jing Yuan-Wei, Jiang Nan, Zhang Si-Ying. Study on the congestion in complex network based on traffic awareness algorithm. Acta Physica Sinica, 2009, 58(10): 6802-6808. doi: 10.7498/aps.58.6802
[20]	Chen Hua-Liang, Liu Zhong-Xin, Chen Zeng-Qiang, Yuan Zhu-Zhi. Research on one weighted routing strategy for complex networks. Acta Physica Sinica, 2009, 58(9): 6068-6073. doi: 10.7498/aps.58.6068

Catalog

Vol. 71, Issue 6 - 2022-03-20

Metrics

Abstract views: 4728
PDF Downloads: 101
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板