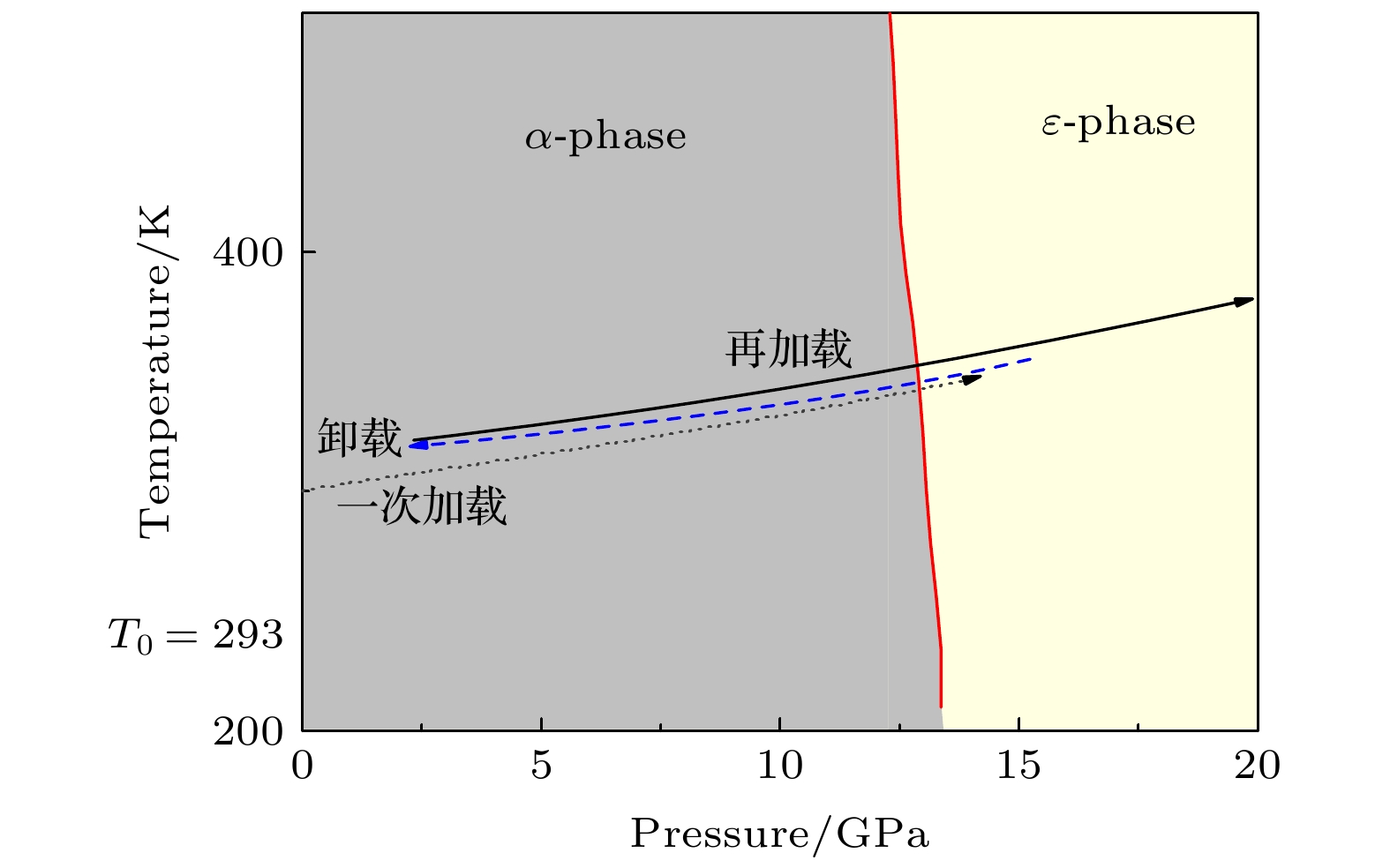
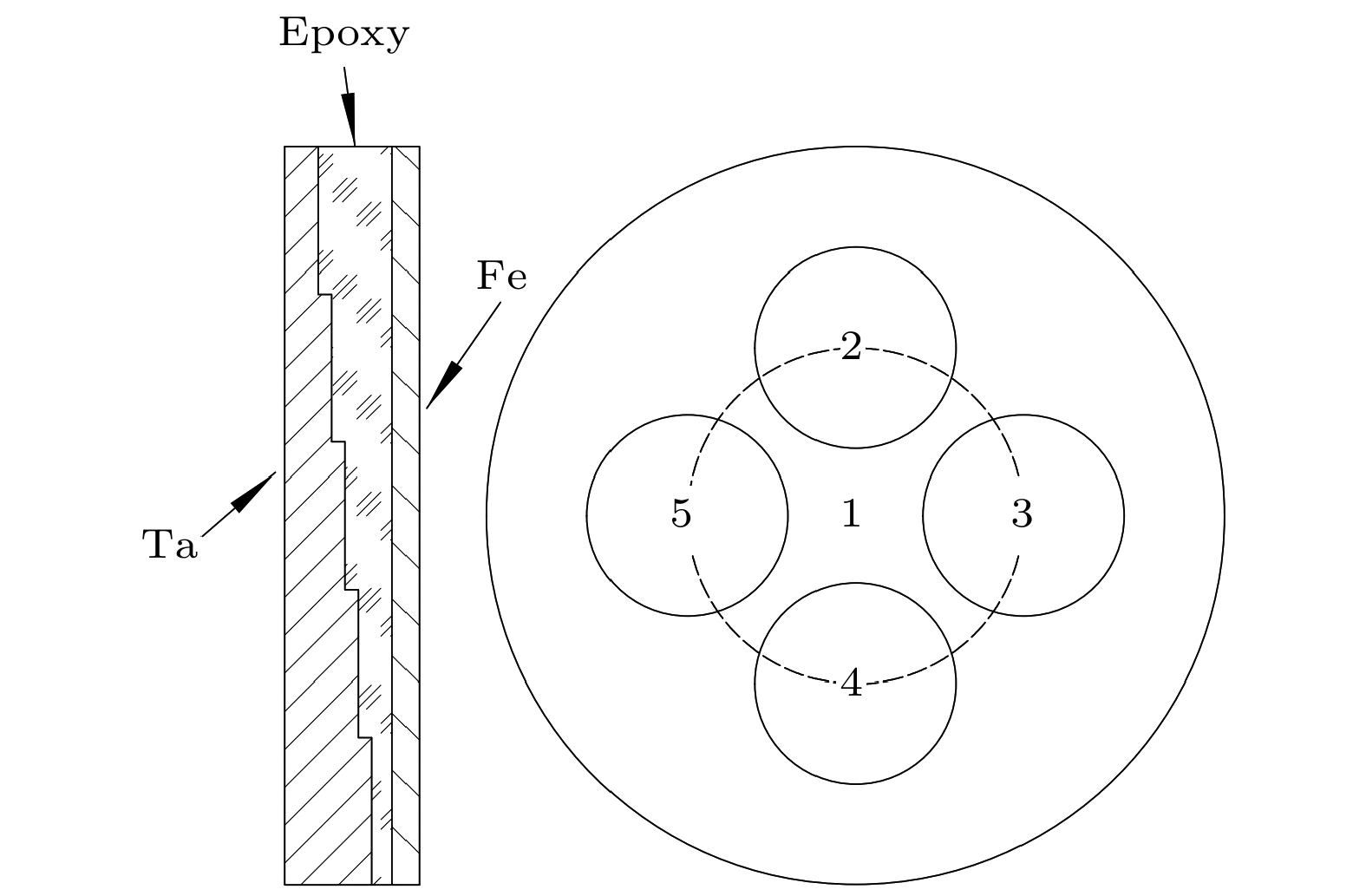
-
The dynamics of iron under extreme conditions like high temperature and high pressure has been well studied for several decades. But, there have been not many reports about the phase transition kinetics coupled with complicated thermodynamic paths, especially loading-unloading-reloading path, which is closer to the real applications. A three-layer structure impactor with five stages performed in the front-surface experiment is made up to approach the special path. We choose epoxy to be the adhesive as it has low impedance and high strength. Tantalum, the standard material of high impedance which also has single wave structure, is selected for reloading process. The wave profile shows a 3-wave structure in the first unloading period and the inverse phase transition threshold is calculated to be about 11.3 GPa. This onset pressure of reverse phase transition is not consistent with Barker’s result, higher than his result (about 2.5 GPa). By comparing with recalculated result of Jensen’s data, we find that our result is consistent with theirs.In this work the inverse phase transition ends at about 10 GPa, the value from this way which is higher than Barker’s finding, even higher than his result of the threshold pressure of reverse phase transition. And at this state there remains 12%–15% of ε phase. So it cannot be seen as the completed reverse phase transformation. The phase transition onset pressure is 10–12 GPa on the reloading path and it is about 1–2 GPa lower than the first phase transition. By simulating the wave profile, the discrepancy of using different phase transformation characteristic time τ as 30 ns and 5 ns is analyzed. It can be seen that the phase transition rate of reloading is faster than that of the first loading process. These phenomena may be caused by the twins and the dislocations which are produced by the inverse phase transition. Also, as unloading time becomes longer, the mass fraction of ε phase becomes lesser and the onset pressure of α → ε phase transition becomes lower. This because with more ε phases transforming into α phase, more twins and dislocations will be produced in material. Therefore, it brings the lower onset pressure.
-
Keywords:
- iron /
- shock loaded /
- kinetics of phase transition /
- reload
[1] Tonkov E Y, Ponyatovsky E G 2004 Phase Transformations of Elements Under High Pressure (Boca Raton: CRC Press) pp53−254, 39−240
[2] Minshall S 1955 J. Appl. Phys. 26 463
Google Scholar
[3] Bancroft D, Peterson E L, Minshall S 1956 J. Appl. Phys. 27 291
Google Scholar
[4] Barker L M, Hollenbach R E 1972 J. Appl. Phys. 43 4669
Google Scholar
[5] Barker L M, Hollenbach R E 1974 J. Appl. Phys. 45 4872
Google Scholar
[6] Balchan A S, Drickamer H G 1961 Rev. Sci. Instrum. 32 308
Google Scholar
[7] Jamison J C, Lawson A W 1962 J. Appl. Phys. 33 776
Google Scholar
[8] Takahashi T, Bassett W A 1964 Science 145 483
Google Scholar
[9] Clenden R L, Drickamer H G 1964 J. Phys. Chem. Solids 25 865
Google Scholar
[10] Jensen B J, GrayⅢ G T, Hixson R S 2009 J. Appl. Phys. 105 103502
Google Scholar
[11] Bastea M, Bastea S, Becker R 2009 Appl. Phys. Lett. 95 241911
Google Scholar
[12] Smith R F, Eggert J H, Swift D C, et al. 2013 J. Appl. Phys. 114 223507
Google Scholar
[13] 施尚春, 陈攀森, 黄跃 1991 高压 5 205
Google Scholar
Shi S C, Chen P S, Huang Y 1991 Chin. J. High Pressure Phys. 5 205
Google Scholar
[14] Tan H, Weng J D, Wang X Proceedings of the 8th National Conference on Explosion Mechanics Ji’an, China, September 20−25, 2007 p75
[15] 谭华 2018 实验冲击波物理 (北京: 国防工业出版社) 第203−218页
Tan H 2018 Experimental Shock Wave Physics (Vol. 1) (Beijing: National Defense Industry Press) pp3−18
[16] Hayes D B W 1975 J. Appl. Phys. 46 3438
Google Scholar
[17] Boettger J C, Wallace D C 1997 1997 Phys. Rev. B 55 2840
[18] 种涛, 唐志平, 谭福利, 王桂吉, 赵剑衡 2018 高压 32 014102
Chong T, Tang Z P, Tan F L, Wang G J, Zhao J H 2018 Chin. J. High Pressure Phys. 32 014102
[19] Dougherty L M, GrayⅢ G T, Cerreta E K, McCabe R J, Field R D, Bingert J F 2009 Scr. Mater. 60 772
Google Scholar
[20] Wang S J, Sui M L, Chen Y T, Lu Q H, M E, Pei X Y, Li Q Z, Hu H B 2013 Sci. Rep. 3 1086
Google Scholar
[21] 唐志平 2008 冲击相变(北京: 科学出版社) 第87−106页
Tang Z P 2008 Shock Phase Transiformation (Vol. 1) (Beijing: Higher Education Press) (in Chinese)
-
图 1 多台阶三层组合飞片结构及台阶分布示意图
Figure 1. Schematic diagram of multistage triple-layer impactor.
图 2 Fe的低压部分相图及热力学加卸载路径设计
Figure 2. The phase diagram of iron and the thermodynamic loading path.
图 3 实验装置系统示意图
Figure 3. Schematic diagram of experimental set up.
图 4 声速计算方法示意图(A点为碰撞时刻, B点为稀疏波到达时刻, C点为卸载过程中任意时刻)
Figure 4. Schematic diagram of sound velocity calculation(A is the impact moment, B is the rarefaction wave arrival time, C is arbitrary time of unloading process).
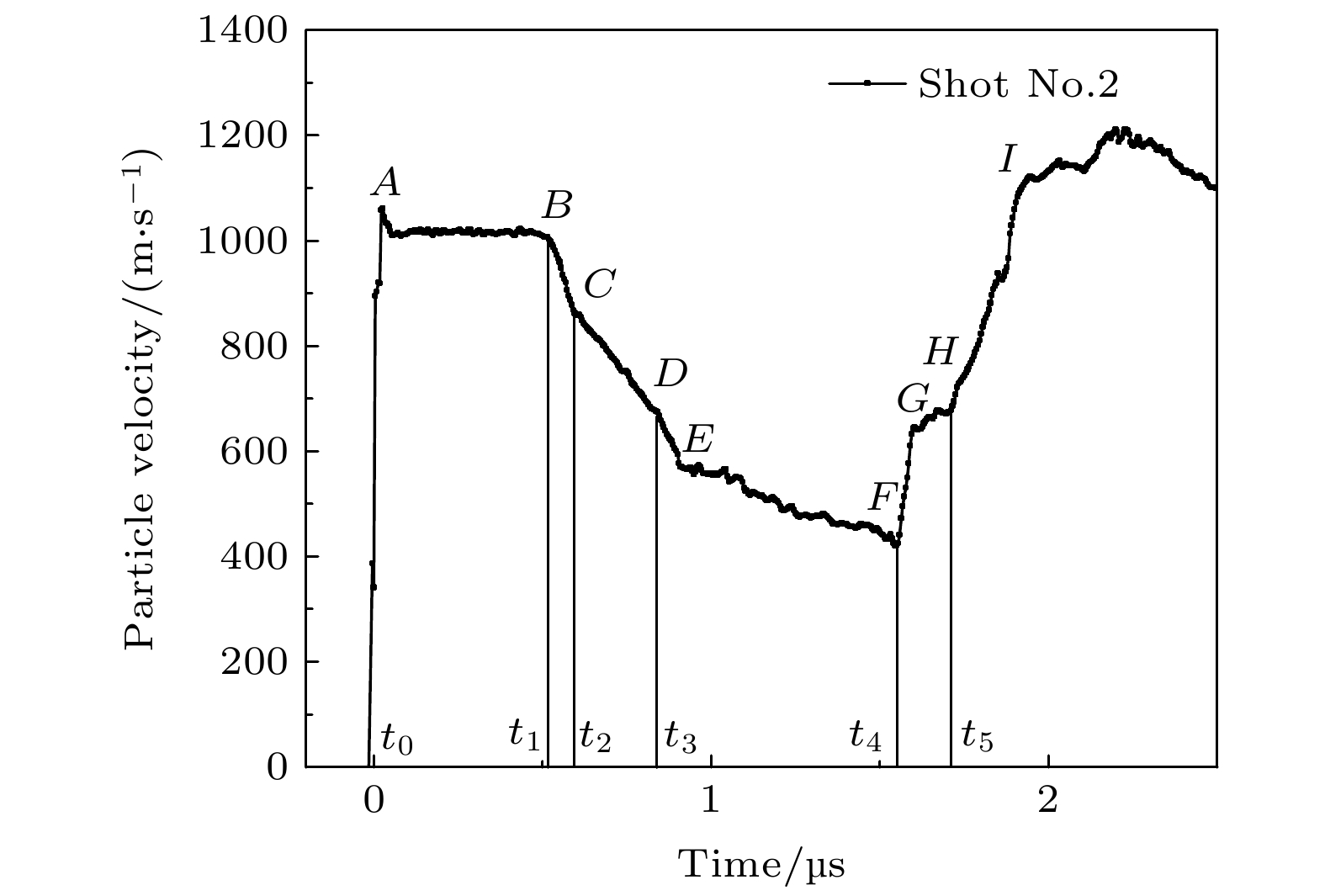
图 5 典型飞片/窗口界面粒子速度剖面(A点为碰撞时刻, B点为稀疏波到达窗口界面, C点为弹塑性卸载拐折点, D点为逆相变起始点, E点为卸载过程终点, F点为二次加载起始点, G为相变临界点, H为再加载P2波到达时刻)
Figure 5. Particle velocity of impactor/window interface (A is the impact moment, B is the rarefaction wave arrival time, C is the elastoplastic unloading crutch point, D is the start point of reverse phase transition, E is the ending of unloading, F is the start point of reloading, G is the phase transition point of the reloading process, H is the reloading P2 wave arrival time).
图 7 (a) shot No.1和(b)shot No.2各台阶对应界面粒子速度历史(1—5分别表示台阶编号)
Figure 7. The interface particle velocity history of all stages in (a) shot No.1 and (b)shot No.2 (1–5 is the serial number of each stage).
图 10 二次相变压力与ε相质量分数关系
Figure 10. The relation between reloading phase transition pressure and mass fraction of ε phase.
表 1 实验材料Hugoniot参数
Table 1. Hugoniot parameter of materials.
材料 $ {{\rho }}_{0}/{({\rm{g}} \cdot {\rm{cm}}}^{-3}) $ $ {{C}}_{0} $/$ ({\rm{km}} \cdot {\rm{s}}^{-1}) $ λ Ta 16.65 3.43 1.19 Epoxy 1.19 2.73 1.49 Fe样品 7.86 3.93 1.58 LiF窗口 2.64 5.21 1.34 
DownLoad: CSV
表 2 实验各部件名义尺寸
Table 2. Gauges of components.
部件 $ {{\rho }}_{0}/\left({{\rm{g}} \cdot {\rm{cm}}}^{-3}\right) $ 直径
/mm厚度
/mm对应Epoxy
厚度/mmTa 1号台阶 16.65 55 2 2.2 Ta 2号台阶 16.65 15 2.5 1.7 Ta 3号台阶 16.65 15 2.8 1.4 Ta 4号台阶 16.65 15 3.2 1.0 Ta 5号台阶 16.65 15 3.5 0.7 Epoxy 1.19 55 — — Fe样品 7.86 55 1.5 — LiF窗口 2.64 55 20 —
DownLoad: CSV
表 3 实验shot No.2测量及计算结果
Table 3. The data of experiment shot No.2.
$ {W}/(\mathrm{m}\cdot {\mathrm{s}}^{-1}) $ $ {{u}}_{\mathrm{w},\mathrm{H}}/(\mathrm{m}\cdot {\mathrm{s}}^{-1}) $ $ {{u}}_{\mathrm{m}}/(\mathrm{m}\cdot {\mathrm{s}}^{-1}) $ $ {{P}}_{\mathrm{m}}/\mathrm{G}\mathrm{P}\mathrm{a} $ $ {{p}}_{\mathrm{D}}/\mathrm{G}\mathrm{P}\mathrm{a} $ $ {{p}}_{\mathrm{E}}/\mathrm{G}\mathrm{P}\mathrm{a} $ $ {\Delta {t}}_{\mathrm{D}\mathrm{E}}/\text{μ}\mathrm{s} $ Shot No.1 1475 ± 15 986 ± 10 489 ± 10 17.0 ± 0.1 11.2 ± 0.4 10.0 ± 0.2 0.08 Shot No.2 1521 ± 15 1015 ± 10 506 ± 10 17.6 ± 0.1 11.4 ± 0.4 10.0 ± 0.2 0.07
DownLoad: CSV
表 4 shot No.1和shot No.2各台阶对应卸载尾段残余ε相质量分数及二次加载相变压力
Table 4. The mass fraction of ε phase in the end of unloading process and reload phase transition pressure on each stage.
Shot No.1 Shot No.2 台阶编号 ε相质量
分数/%二次加载相
变压力/GPaε相质量
分数/%二次加载相
变压力/GPa5 52 11.5 77 12.0 4 27 10.9 36 11.1 3 21 10.6 26 10.8 2 16 10.4 20 10.5 1 12 10.1 15 10.2
DownLoad: CSV
-
[1] Tonkov E Y, Ponyatovsky E G 2004 Phase Transformations of Elements Under High Pressure (Boca Raton: CRC Press) pp53−254, 39−240
[2] Minshall S 1955 J. Appl. Phys. 26 463
Google Scholar
[3] Bancroft D, Peterson E L, Minshall S 1956 J. Appl. Phys. 27 291
Google Scholar
[4] Barker L M, Hollenbach R E 1972 J. Appl. Phys. 43 4669
Google Scholar
[5] Barker L M, Hollenbach R E 1974 J. Appl. Phys. 45 4872
Google Scholar
[6] Balchan A S, Drickamer H G 1961 Rev. Sci. Instrum. 32 308
Google Scholar
[7] Jamison J C, Lawson A W 1962 J. Appl. Phys. 33 776
Google Scholar
[8] Takahashi T, Bassett W A 1964 Science 145 483
Google Scholar
[9] Clenden R L, Drickamer H G 1964 J. Phys. Chem. Solids 25 865
Google Scholar
[10] Jensen B J, GrayⅢ G T, Hixson R S 2009 J. Appl. Phys. 105 103502
Google Scholar
[11] Bastea M, Bastea S, Becker R 2009 Appl. Phys. Lett. 95 241911
Google Scholar
[12] Smith R F, Eggert J H, Swift D C, et al. 2013 J. Appl. Phys. 114 223507
Google Scholar
[13] 施尚春, 陈攀森, 黄跃 1991 高压 5 205
Google Scholar
Shi S C, Chen P S, Huang Y 1991 Chin. J. High Pressure Phys. 5 205
Google Scholar
[14] Tan H, Weng J D, Wang X Proceedings of the 8th National Conference on Explosion Mechanics Ji’an, China, September 20−25, 2007 p75
[15] 谭华 2018 实验冲击波物理 (北京: 国防工业出版社) 第203−218页
Tan H 2018 Experimental Shock Wave Physics (Vol. 1) (Beijing: National Defense Industry Press) pp3−18
[16] Hayes D B W 1975 J. Appl. Phys. 46 3438
Google Scholar
[17] Boettger J C, Wallace D C 1997 1997 Phys. Rev. B 55 2840
[18] 种涛, 唐志平, 谭福利, 王桂吉, 赵剑衡 2018 高压 32 014102
Chong T, Tang Z P, Tan F L, Wang G J, Zhao J H 2018 Chin. J. High Pressure Phys. 32 014102
[19] Dougherty L M, GrayⅢ G T, Cerreta E K, McCabe R J, Field R D, Bingert J F 2009 Scr. Mater. 60 772
Google Scholar
[20] Wang S J, Sui M L, Chen Y T, Lu Q H, M E, Pei X Y, Li Q Z, Hu H B 2013 Sci. Rep. 3 1086
Google Scholar
[21] 唐志平 2008 冲击相变(北京: 科学出版社) 第87−106页
Tang Z P 2008 Shock Phase Transiformation (Vol. 1) (Beijing: Higher Education Press) (in Chinese)
DownLoad:
Catalog
Metrics
- Abstract views: 4228
- PDF Downloads: 101
- Cited By: 0
