-
Pattern formation and self-organization are ubiquitous in nature and commonly observed in spatially extended non-equilibrium systems. As is well known, the origin of spatio-temporal patterns can be traced to the instability of the system, and is always accompanied by a symmetry breaking phenomenon. In reality, most of non-equilibrium systems are constructed by interactions among several different units, each of which has its unique symmetry breaking mechanism. The interaction among different units described by coupled pattern forming system gives rise to a variety of self-organized patterns including stationary and/or oscillatory patterns. In this paper, the dynamics of oscillatory Turing patterns in two-layered coupled non-symmetric reaction diffusion systems are numerically investigated by linearly coupling the Brusselator model and the Lengyel-Epstein model. The interaction among the Turing modes, higher-order harmonics and Hopf mode, and their effects on oscillatory Turing pattern are also analyzed. It is shown that the supercritical Turing mode
${k_1}$ in the Lengyel-Epstein model is excited and interacts with the higher-order harmonics$\sqrt 3 {k_1}$ located in the Hopf region in the Brusselator model, and thus giving rise to the synchronous oscillatory hexagon pattern. The harmonic$\sqrt 2 {k_1}$ that can also be excited initially is some parameter domain, but it is unstable and vanishes finally. As the parameter b is increased, this oscillatory hexagon pattern first undergoes period-doubling bifurcation and transits into two-period oscillation, and then into multiple-period oscillation. When the Hopf mode participates in the interaction, the pattern will eventually transit into chaos. The synchronous oscillatory hexagon pattern can only be obtained when the subcritical Turing mode${k_2}$ in the Brusselator model is weaker than the higher-order harmonics$\sqrt 3 {k_1}$ located in the Hopf region and neither of the two Turing modes satisfies the spatial resonance condition. The system favorites the spatial resonance and selects the super-lattice patterns when these modes interact with each other. The interaction between Hopf mode and Turing mode can only give rise to non-synchronous oscillatory patterns. Moreover, the coupling strength also has an important effect on the oscillatory Turing pattern. These results not only provide a new pattern forming mechanism which can be extended to other nonlinear systems, but also gives an opportunity for more in-depth understanding the nature and their relevance to technological applications.-
Keywords:
- non-symmetric coupled reaction diffusion system /
- oscillatory Turing patterns /
- Turing mode /
- higher-order mode /
- Hopf mode
[1] Marino F, Giacomelli G 2019 Phys. Rev. Lett. 122 174102
Google Scholar
[2] Bleicher P, Sciortino A, Bausch A R 2020 Sci. Rep. 10 62151
Google Scholar
[3] Fencl M 2020 Nonlinear Anal. Theory Methods Appl. 196 111815
Google Scholar
[4] Gao Y P, Zhang Y F, Schwen D, Jiang C, Gan J 2019 Sci. Rep. 9 7835
Google Scholar
[5] Dong L F, Mi Y L, Pan Y Y 2020 Phys. Plasmas 27 023504
Google Scholar
[6] Yu G L, Dong L F, Guo L T, Liu F C, Li C X, Dou Y Y, Ren C H, Pan Y Y 2020 Phys. Plasmas 27 053503
Google Scholar
[7] 郑志刚, 翟云 2020 中国科学: 物理学 力学 天文学 50 69
Google Scholar
Zheng Z G, Zhai Y 2020 Sci. China, Ser. G 50 69
Google Scholar
[8] Gao J, Gu C G 2019 IEEE Access 7 140391
Google Scholar
[9] Gu L C, Gong P L, Wang H Q 2020 Discrete Dyn. Nat. Soc. 2020 5293748
[10] Yang R, Song Y L 2016 Nonlinear Anal. Real World Appl. 31 356
Google Scholar
[11] Dolnik M, Rovinsky A B, Zhabotinsky A M, Epstein I R 1999 J. Phys. Chem. A 103 38
Google Scholar
[12] Yang L F, Zhabotinsky A M, Epstein I R 2004 Phys. Rev. Lett. 92 198303
Google Scholar
[13] Zhabotinsky A M, Dolnik M, Epstein I R 1995 J. Chem. Phys. 103 10306
Google Scholar
[14] Konishi K, Hara N 2018 Phys. Rev. E 97 052201
Google Scholar
[15] 李新政, 白占国, 李燕 2019 68 068201
Google Scholar
Li X Z, Bai Z G, Li Y 2019 Acta Phys. Sin. 68 068201
Google Scholar
[16] Paquin-Lefebvre F, Xu B, Dipietro K L, Lindsay A E, Jilkine A 2020 J. Theor. Biol. 497 110242
Google Scholar
[17] Yang L F, Dolnik M, Zhabotinsky A M, Epstein I R 2002 Phys. Rev. Lett. 88 208303
Google Scholar
[18] Yang L F, Epstein I R 2003 Phys. Rev. Lett. 90 178303
Google Scholar
[19] Anguelov R, Stoltz S M 2017 Math. Comput. Simul. 133 39
Google Scholar
[20] Li X Z, Bai Z G, Li Y, Zhao K 2016 Mod. Phys. Lett. B 30 1650085
Google Scholar
[21] Pal K, Paul S, Ray D S 2020 Phys. Rev. E 101 052203
Google Scholar
[22] Scarabotti P, Govezensky T, Bolcatto P 2020 Sci. Rep. 10 124451
[23] Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D U 2006 Phys. Rep. 424 175
Google Scholar
[24] Li C X, Dong L F, Feng J Y, Huang Y P 2019 Phys. Plasmas 26 023505
Google Scholar
[25] Callegari T, Bernecker B, Boeuf J P 2014 Plasma Sources Sci. Technol. 23 054003
Google Scholar
[26] Trelles J P 2016 J. Phys. D: Appl. Phys. 49 393002
Google Scholar
[27] 陈俊英, 董丽芳, 李媛媛, 宋倩, 嵇亚飞 2012 61 075211
Google Scholar
Chen J Y, Dong L F, Li Y Y, Song Q, Ji Y F 2012 Acta Phys. Sin. 61 075211
Google Scholar
[28] Feng J Y, Pan Y Y, Li C X, Liu B B, Dong L F 2020 Phys. Plasmas 27 063516
Google Scholar
[29] Dong L F, Li B, Shen Z K, Liu L 2012 Phys. Rev. E 86 056217
Google Scholar
[30] Dong L F, Shen Z K, Li B, Bai Z G 2013 Phys. Rev. E 87 042914
Google Scholar
[31] 刘富成, 刘雅慧, 周志向, 郭雪, 董梦菲 2020 69 028201
Google Scholar
Liu F C, Liu Y H, Zhou Z X, Guo X, Dong M F 2020 Acta Phys. Sin. 69 028201
Google Scholar
[32] Gambino G, Lombardo M C, Sammartino M, Sciacca V 2013 Phys. Rev. E 88 042925
Google Scholar
[33] Li J, Wang H L, Ouyang Q 2014 Chaos 24 023115
Google Scholar
[34] 冯建宇, 董丽芳, 魏领燕 2016 发光学报 37 1076
Google Scholar
Feng J Y, Dong L F, Wei L Y 2016 Chin. J. Chromatogr. 37 1076
Google Scholar
[35] Dong L F, Liu W L, Wang H F, He Y F, Fan W L, Gao R L 2007 Phys. Rev. E 76 046210
Google Scholar
[36] Dai D, Zhao X F, Wang Q M 2014 EPL 107 15002
Google Scholar
[37] 王敩青, 戴栋, 郝艳捧, 李立浧 2012 61 230504
Google Scholar
Wang X Q, Dai D, Hao Y P, Li L C 2012 Acta Phys. Sin. 61 230504
Google Scholar
[38] Zhang J, Wang Y H, Wang D Z, Zhuang J 2014 Plasma Sci. Technol. 16 110
Google Scholar
[39] Dong L F, Li B, Lu N, Li X C, Shen Z K 2012 Phys. Plasmas 19 052304
Google Scholar
-
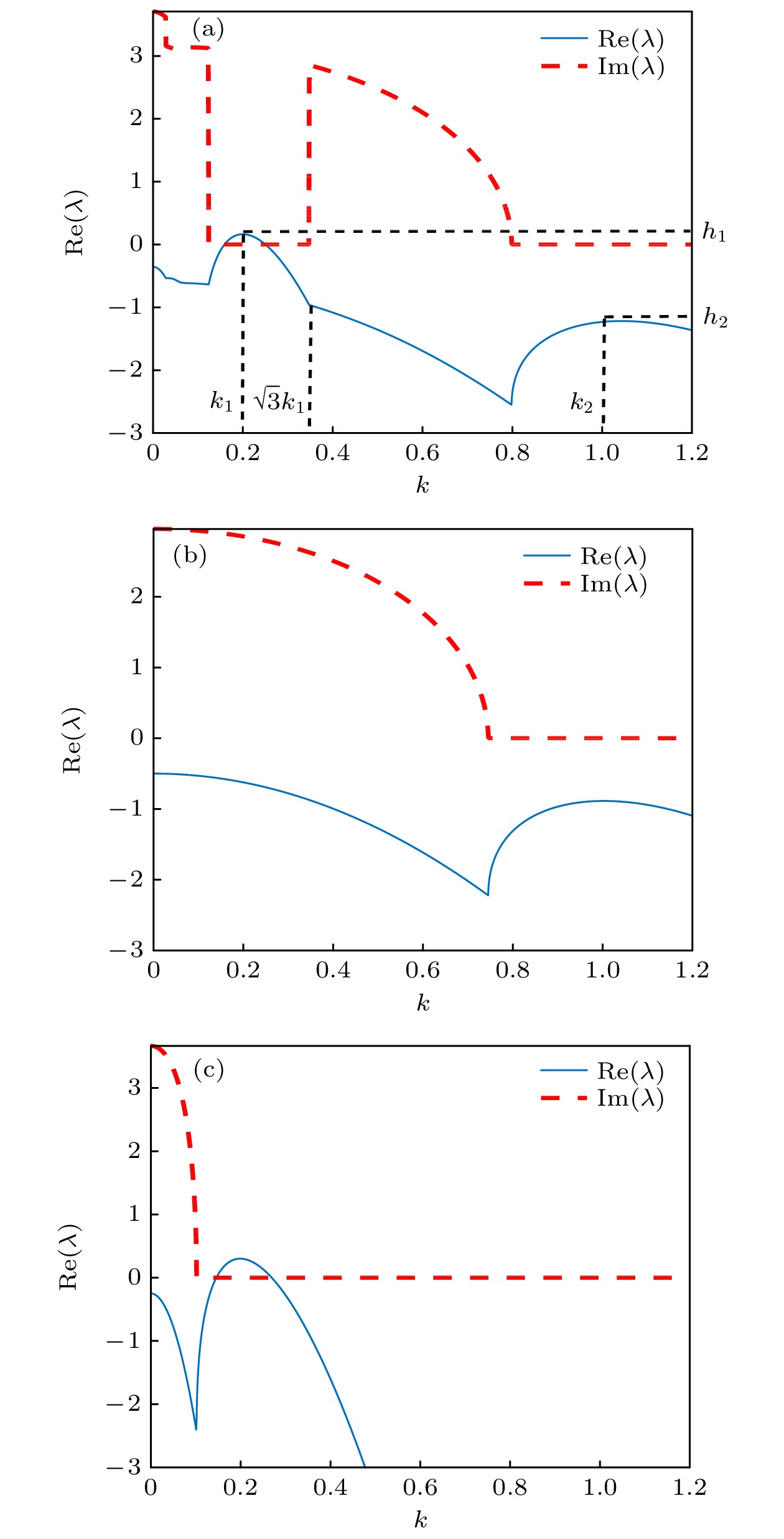
图 1 双层线性耦合系统以及单层系统的色散关系 (a) 双层线性耦合系统; (b) 单层Brusselator模型; (c) 单层Lengyel-Epstein模型. 参数取值为:
$( a, b) = (3, 9)$ ,$(c, d) = $ $ (15, \;9)$ ,${D_{{u_1}}} = 2.2$ ,${D_{{v_1}}} = 4.0$ ,${D_{{u_2}}} =21.9$ ,${D_{{v_2}}} = $ $ 400,$ $\alpha = 0.15$ Figure 1. Dispersion relationship of two-layered linear coupling system and single layer system: (a) Two-layered linear coupling system; (b) single layer Brusselator model; (c) single layer Lengyel-Epstein model. Parameter:
$(a, b) = (3, 9)$ ,$ \left( {c, d} \right) = \left( {15, 9} \right)$ ,${D_{{u_1}}} = 2.2$ ,${D_{{v_1}}} = 4.0$ ,${D_{{u_2}}} = 21.9$ ,${D_{{v_2}}} = $ $ 400$ ,$\alpha = 0.15$ 
图 3 参数 b对时空斑图的影响 (a) 不同参数b下的色散关系曲线; (b1)静态蜂窝状六边形斑图,
$b = 8.5$ ; (b2)单倍周期同步振荡六边形斑图,$ b =9$ ; (b3) 2倍周期非同步振荡六边形斑图,$ b =9.25$ ; (b4) 5倍周期非同步振荡六边形斑图,$ b =9.33$ ; (b5) 3倍周期非同步振荡斑图,$ b =9.5$ ; (b6)时空混沌,$ b =10$ Figure 3. Influence of parameter bon spatio-temporal patterns: (a) Dispersion curves under different parameters b; (b1) static honeycomb hexagon pattern at
$b = 8.5$ ; (b2) single-period synchronous oscillation hexagon pattern at$b = 9$ ; (b3) non-synchronous oscillation hexagon pattern of 2 times the period at$b = 9.25$ ; (b4) non-synchronous oscillation hexagon pattern of 5 times the period at$b = 9.33$ ; (b5) non-synchronous oscillation pattern of 3 times the period at$b = 9.5$ ; (b6) spatio-temporal chaos at$b = 10$ .
图 4 非共振时不同本征值
${h_2}$ 下的时空斑图 (a) 不同本征值${h_2}$ 下的色散关系曲线; (b1) 静态蜂窝状六边形斑图,${h_2} = - 5.50$ ,${D_{{u_1}}} = 5.25$ ,${D_{{v_1}}} = 6.5$ ; (b2) 同步振荡六边形斑图,${h_2} = - 3.44$ ,${D_{u{}_1}} = 3.62$ ,${D_{{v_1}}} = 5$ ; (b3) 超六边形斑图,${h_2} = - 0.56$ ,${D_{{u_1}}} = 2.2$ ,${D_{{v_1}}} = 4.6$ ; (b4) 叠加斑图,${h_2} = - 0.21$ ,${D_{{u_1}}} = 2.1$ ,${D_{v{}_1}} = 4.8$ ; (b5)混合斑图,${h_2} = 0.26$ ,${D_{{u_1}}} = 2.03$ ,${D_{{v_1}}} = $ $ 5.3$ ; (b6) 条纹斑图,${h_2} = 0.62$ ,${D_{{u_1}}} = 1.98$ ,${D_{{v_1}}} = 5.8$ Figure 4. Complex patterns under different eigenvalues
${h_2}$ at non-resonance: (a) Dispersion curves under different eigenvalues${h_2}$ ; (b1) static honeycomb hexagon pattern,${h_2} = - 5.50$ ,${D_{{u_1}}} = 5.25$ ,${D_{{v_1}}} = 6.5$ ; (b2) synchronous oscillation hexagon pattern,${h_2} = - 3.44$ ,${D_{{u_1}}} = 3.62$ ,${D_{{v_1}}} = 5$ ; (b3) super-hexagon pattern,${h_2} = - 0.56$ ,${D_{{u_1}}} = 2.2$ ,${D_{{v_1}}} = 4.6$ ; (b4) superposition pattern,${h_2} = - 0.21$ ,${D_{{u_1}}} = 2.1$ ,${D_{{v_1}}} = 4.8$ ; (b5) hybrid pattern,${h_2} = 0.26$ ,${D_{{u_1}}} = 2.03$ ,${D_{{v_1}}} = 5.3$ ; (b6) stripe pattern,${h_2} = 0.62$ ,${D_{{u_1}}} = 1.98$ ,${D_{{v_1}}} = 5.8$ .
图 5 共振时不同本征值
${h_2}$ 下的时空斑图 (a) 不同本征值${h_2}$ 下的色散关系曲线; (b1)静态蜂窝状六边形斑图,${h_2} = - 1.7$ ,${D_{{u_1}}} \!=\! 14.55$ ,${D_{{v_1}}} \!=\! 24$ ; (b2) 静态黑眼斑图,${h_2} \!=\! - 1.1$ ,${D_{{u_1}}} \!=\! 13.6$ ,${D_{{v_1}}} \!=\! 25$ ; (b3) 条纹斑图,${h_2} \!=\! 1.0$ ,${D_{{u_1}}} \!=\! 12$ ,${D_{{v_1}}} \!=\! 40$ Figure 5. Spatiotemporal patterns under different eigenvalues
${h_2}$ at resonance: (a) Dispersion curves under different eigenvalues${h_2}$ ; (b1) static honeycomb hexagon pattern,${h_2} = - 1.7$ ,${D_{{u_1}}} = 14.55$ ,${D_{{v_1}}} = 24$ ; (b2) static black eye pattern,${h_2} = - 1.1$ ,${D_{{u_1}}} = 13.6$ ,${D_{{v_1}}} = 25$ ; (b3) stripe pattern,${h_2} = 1.0$ ,${D_{{u_1}}} = 12$ ,${D_{{v_1}}} = 40$ .
图 6 不同耦合强度下的时空斑图(其他参数同图1) (a) 不同耦合强度下的色散关系曲线图; (b1)静态蜂窝状六边形斑图,
$\alpha = 0.1$ ; (b2)同步振荡六边形斑图,$\alpha = 0.17$ ; (b3)非同步振荡六边形斑图,$\alpha = 0.3$ ; (b4)均匀态,$\alpha = 0.6$ Figure 6. Spatio-temporal patterns under different coupling intensities at non-resonance: (a) Dispersion relationship curve diagram under different coupling intensities; (b1) static honeycomb hexagon pattern at
$\alpha = 0.1$ ; (b2) synchronous oscillation hexagon pattern at$\alpha = 0.17$ ; (b3) non-synchronous oscillation hexagon pattern at$\alpha = 0.3$ ; (b4) uniform state at$\alpha = 0.6$ . Other parameters are the same as those in Fig. 1.
图 7 振荡黑眼斑图(
$\left( {a, b} \right) = \left( {3, 10.5} \right)$ ,$\left( {c, d} \right) = \left( {15, 9} \right)$ ,${D_{{u_1}}} = 15$ ,${D_{{v_1}}} = 23$ ,${D_{{u_2}}} = 21.9$ ,${D_{{v_2}}} = 400$ ,$\alpha = 0.45$ ) (a) 耦合系统的色散关系曲线; (b) 振幅分布; (c) 3个位置处${u_1}$ 的时间变化关系图; (d) 斑图演化过程Figure 7. Oscillatory black-eye pattern (
$\left( {a, b} \right) = \left( {3, 10.5} \right)$ ,$\left( {c, d} \right) = \left( {15, 9} \right)$ ,${D_{u1}} = 15$ ,${D_{v1}} = 23$ ,${D_{u2}} = 21.9$ ,${D_{v2}} = 400$ ,$\alpha = 0.45$ ): (a) Dispersion curve of coupled system; (b) amplitude distribution; (c) time variation of${u_1}$ at three positions; (d) evolution of pattern. -
[1] Marino F, Giacomelli G 2019 Phys. Rev. Lett. 122 174102
Google Scholar
[2] Bleicher P, Sciortino A, Bausch A R 2020 Sci. Rep. 10 62151
Google Scholar
[3] Fencl M 2020 Nonlinear Anal. Theory Methods Appl. 196 111815
Google Scholar
[4] Gao Y P, Zhang Y F, Schwen D, Jiang C, Gan J 2019 Sci. Rep. 9 7835
Google Scholar
[5] Dong L F, Mi Y L, Pan Y Y 2020 Phys. Plasmas 27 023504
Google Scholar
[6] Yu G L, Dong L F, Guo L T, Liu F C, Li C X, Dou Y Y, Ren C H, Pan Y Y 2020 Phys. Plasmas 27 053503
Google Scholar
[7] 郑志刚, 翟云 2020 中国科学: 物理学 力学 天文学 50 69
Google Scholar
Zheng Z G, Zhai Y 2020 Sci. China, Ser. G 50 69
Google Scholar
[8] Gao J, Gu C G 2019 IEEE Access 7 140391
Google Scholar
[9] Gu L C, Gong P L, Wang H Q 2020 Discrete Dyn. Nat. Soc. 2020 5293748
[10] Yang R, Song Y L 2016 Nonlinear Anal. Real World Appl. 31 356
Google Scholar
[11] Dolnik M, Rovinsky A B, Zhabotinsky A M, Epstein I R 1999 J. Phys. Chem. A 103 38
Google Scholar
[12] Yang L F, Zhabotinsky A M, Epstein I R 2004 Phys. Rev. Lett. 92 198303
Google Scholar
[13] Zhabotinsky A M, Dolnik M, Epstein I R 1995 J. Chem. Phys. 103 10306
Google Scholar
[14] Konishi K, Hara N 2018 Phys. Rev. E 97 052201
Google Scholar
[15] 李新政, 白占国, 李燕 2019 68 068201
Google Scholar
Li X Z, Bai Z G, Li Y 2019 Acta Phys. Sin. 68 068201
Google Scholar
[16] Paquin-Lefebvre F, Xu B, Dipietro K L, Lindsay A E, Jilkine A 2020 J. Theor. Biol. 497 110242
Google Scholar
[17] Yang L F, Dolnik M, Zhabotinsky A M, Epstein I R 2002 Phys. Rev. Lett. 88 208303
Google Scholar
[18] Yang L F, Epstein I R 2003 Phys. Rev. Lett. 90 178303
Google Scholar
[19] Anguelov R, Stoltz S M 2017 Math. Comput. Simul. 133 39
Google Scholar
[20] Li X Z, Bai Z G, Li Y, Zhao K 2016 Mod. Phys. Lett. B 30 1650085
Google Scholar
[21] Pal K, Paul S, Ray D S 2020 Phys. Rev. E 101 052203
Google Scholar
[22] Scarabotti P, Govezensky T, Bolcatto P 2020 Sci. Rep. 10 124451
[23] Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D U 2006 Phys. Rep. 424 175
Google Scholar
[24] Li C X, Dong L F, Feng J Y, Huang Y P 2019 Phys. Plasmas 26 023505
Google Scholar
[25] Callegari T, Bernecker B, Boeuf J P 2014 Plasma Sources Sci. Technol. 23 054003
Google Scholar
[26] Trelles J P 2016 J. Phys. D: Appl. Phys. 49 393002
Google Scholar
[27] 陈俊英, 董丽芳, 李媛媛, 宋倩, 嵇亚飞 2012 61 075211
Google Scholar
Chen J Y, Dong L F, Li Y Y, Song Q, Ji Y F 2012 Acta Phys. Sin. 61 075211
Google Scholar
[28] Feng J Y, Pan Y Y, Li C X, Liu B B, Dong L F 2020 Phys. Plasmas 27 063516
Google Scholar
[29] Dong L F, Li B, Shen Z K, Liu L 2012 Phys. Rev. E 86 056217
Google Scholar
[30] Dong L F, Shen Z K, Li B, Bai Z G 2013 Phys. Rev. E 87 042914
Google Scholar
[31] 刘富成, 刘雅慧, 周志向, 郭雪, 董梦菲 2020 69 028201
Google Scholar
Liu F C, Liu Y H, Zhou Z X, Guo X, Dong M F 2020 Acta Phys. Sin. 69 028201
Google Scholar
[32] Gambino G, Lombardo M C, Sammartino M, Sciacca V 2013 Phys. Rev. E 88 042925
Google Scholar
[33] Li J, Wang H L, Ouyang Q 2014 Chaos 24 023115
Google Scholar
[34] 冯建宇, 董丽芳, 魏领燕 2016 发光学报 37 1076
Google Scholar
Feng J Y, Dong L F, Wei L Y 2016 Chin. J. Chromatogr. 37 1076
Google Scholar
[35] Dong L F, Liu W L, Wang H F, He Y F, Fan W L, Gao R L 2007 Phys. Rev. E 76 046210
Google Scholar
[36] Dai D, Zhao X F, Wang Q M 2014 EPL 107 15002
Google Scholar
[37] 王敩青, 戴栋, 郝艳捧, 李立浧 2012 61 230504
Google Scholar
Wang X Q, Dai D, Hao Y P, Li L C 2012 Acta Phys. Sin. 61 230504
Google Scholar
[38] Zhang J, Wang Y H, Wang D Z, Zhuang J 2014 Plasma Sci. Technol. 16 110
Google Scholar
[39] Dong L F, Li B, Lu N, Li X C, Shen Z K 2012 Phys. Plasmas 19 052304
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4966
- PDF Downloads: 112
- Cited By: 0
