-
In this paper, we propose a new type of relativistic regional innovation index by using the international patent application data. Based on the super-linear relationship between regional innovation and economic development, the new index can eliminate the influence of economic development level on innovation capabilities, and can effectively achieve the comparison of innovation capabilities among economies at different economic development levels. This new index is quite simple, and points out a series of new findings that are sharply different from the traditional cognitive phenomena, e.g. the index shows that the technological innovation capabilities of mainland China are among the highest in the world in 1980s. Moreover, the use of this new index not only can efficiently explain the economic growth of countries in the world at a higher level, but also find that there is a novel 20-year business cycle in the correlation between the index and economic growth rate. These results show that the index, as a simple single indicator, can achieve a higher degree of explanatory ability with minimal data dependence. This new index not only repositions the innovation capacity of world’s economies, but also provides a new insight into an in-depth understanding of the relationship between innovation and economic development, and implies the development potential and application space such a kind of relativistic economic indicator.
-
Keywords:
- regional innovation index /
- business cycle /
- relativistic economic indicator /
- complexity in economy
[1] Hansen T, Winther L 2011 Eur. Urban Reg. Stud. 18 321
 Google Scholar
Google Scholar
[2] Fagerberg J E, Srholec M 2008 Res. Policy 37 1417
 Google Scholar
Google Scholar
[3] Wignaraja G 2012 J. Asian Econ. 23 224
 Google Scholar
Google Scholar
[4] Mohnen P, Dagenais M 2002 Towards an Innovation Intensity Index: The Case of CIS 1 in Denmark and Ireland In: Innovation and Firm Performance (London: Kleinknecht A, Mohnen P, eds.) pp3–30
[5] Slaper T F, Hart N R, Hall T J, Thompson M F 2011 Econ. Dev. Q. 25 36
 Google Scholar
Google Scholar
[6] Clayton T, Borgo M D, Haskel J 2009 https://ssrn.com/ abstract=1345684
[7] Żelazny R, Pietrucha J 2017 Q. J. Econ. Econ. Policy 12 43
[8] Crespo N F, Crespo C F 2016 J. Bus. Res. 69 5265
 Google Scholar
Google Scholar
[9] Sohn S Y, Kim D H, Jeon S Y 2016 Technol. Anal. Strateg. Manag. 28 492
 Google Scholar
Google Scholar
[10] McGrath M E, Romeri M N 1994 J. Prod. Innov. Manag. 11 213
 Google Scholar
Google Scholar
[11] Narin F, Olivastro D 1988 Technology Indicators Based On Patents And Patent Citations In: Handbook of Quantitative Studies of Science and Technology (Amsterdam: Van Raan A F J, eds.) pp465–507
[12] Guan J C, Gao X 2009 J. Associat. Inf. Sci. Technol. 60 35
 Google Scholar
Google Scholar
[13] Csajbók E, Berhidi A, Vasas L, et al. 2007 Scientometrics 73 91
 Google Scholar
Google Scholar
[14] Mester G 2016 Interdiscipl. Descript. Compl. Syst. 14 1
 Google Scholar
Google Scholar
[15] Gao H 2014 Internat. J. Adv. Manag. Sci. 3 128
 Google Scholar
Google Scholar
[16] May M, Brody H 2015 Nature 522 S1
 Google Scholar
Google Scholar
[17] Haunschild R, Bornmann L 2015 Scientometrics 102 1829
 Google Scholar
Google Scholar
[18] 中国区域创新指数报告课题组 2019 中国西部 2019 19
 Google Scholar
Google Scholar
Report of China Regional Innovation Index Research Group 2019 Western China 2019 19
 Google Scholar
Google Scholar
[19] Bettencourt L M A, Lobo J, Helbing D, Kühnert C, West G B 2007 Proc. Natl. Acad. Sci. U. S. A. 104 7301
 Google Scholar
Google Scholar
[20] Bettencourt L M A, West G B 2010 Nature 467 912
 Google Scholar
Google Scholar
[21] Arbesman S, Kleinberg J M, Strogatz S H 2009 Phys. Rev. E 79 16115
 Google Scholar
Google Scholar
[22] Wunsch-Vincent S, Lanvin B, Dutta S 2015 eSocialSciences Working Paper id: 7491
[23] Hirooka M 2003 J. Evol. Econ. 13 549
 Google Scholar
Google Scholar
[24] Groot B de, Franses P H 2009 Technol. Forecast. Social Chang. 76 1021
 Google Scholar
Google Scholar
[25] Hausman A, Johnston W J 2014 J. Bus. Res. 67 2720
 Google Scholar
Google Scholar
[26] Gao J, Zhang Y C, Zhou T 2019 Phys. Rep. 817 1
 Google Scholar
Google Scholar
[27] Hidalgo C A, Klinger B, Barabási A L, Hausmann R 2007 Science 317 482
 Google Scholar
Google Scholar
[28] Hidalgo C A, Hausmann R 2009 Proc. Natl. Acad. Sci. U.S.A. 106 10570
 Google Scholar
Google Scholar
[29] Caldarelli G, Cristelli M, Gabrielli A, Pietronero L, Scala A, Tacchella A 2012 PLoS ONE 7 e47278
 Google Scholar
Google Scholar
[30] Cristelli M, Gabrielli A, Tacchella A, Caldarelli G, Pietronero L 2013 PLoS ONE 8 e70726
 Google Scholar
Google Scholar
[31] Neffke F, Henning M, Boschma R 2011 Econ. Geogr. 87 237
 Google Scholar
Google Scholar
[32] Tacchella A, Mazzilli D, Pietronero L 2018 Nat. Phys. 14 861
 Google Scholar
Google Scholar
-
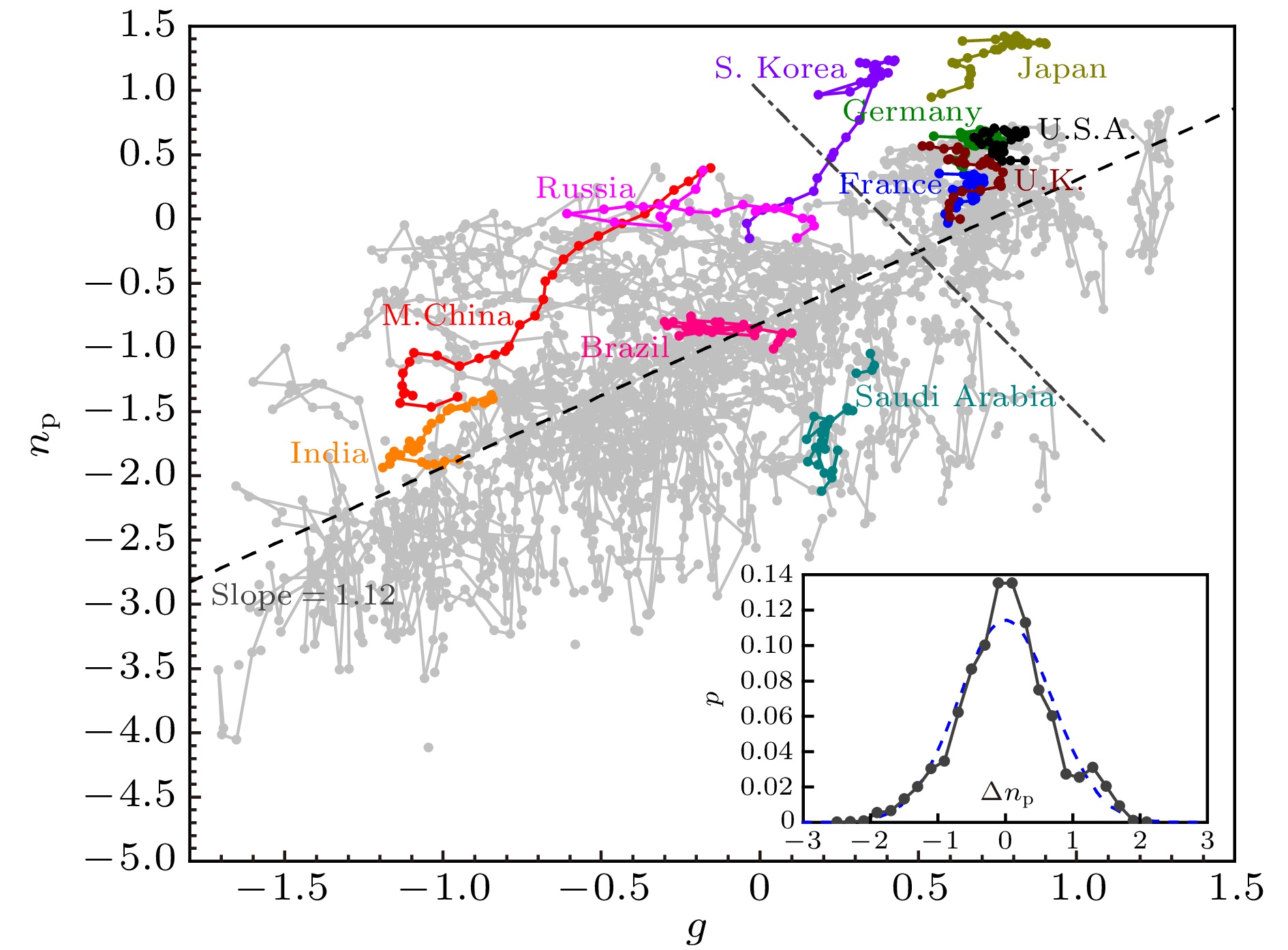
图 1 世界各经济体在由相对人均GDP的对数g和相对人均专利申请数的对数np(两者均以10为底数)所构成的空间中的变化轨迹. 彩色曲线为11个代表性经济体在该空间的轨迹, 灰色曲线为其他经济体. 灰色虚线为拟合直线np = 1.12g – 0.82. 灰色点划线大致区分了发达经济体的轨迹所在区域和发展中经济体所在区域, 右上方主要为发达经济体, 左下方主要为发展中经济体. 插图显示了各个数据点相对拟合直线的离差Δnp的概率分布, 蓝色虚线为其高斯函数拟合
Figure 1. The trajectories of economies from 1985 to 2017 in the space of the logarithmic relative GDP per capita (g) and the logarithmic relative number of patent applications per capita (np). The colored curves and gray curves represent the trajectory of 11 representative economies and the remain economies, respectively. The gray dashed line is the fitting function np = 1.12g – 0.82 of all data points. The gray dot dash line roughly distinguishes between the developed economies and the developing economies. Developed economies are mainly in the upper right area, while developing economies are in the lower left. The inset plots the distribution of the deviation Δnp of each data point from the fitting line, in which the blue dashed line is its Gaussian fitting.
图 4 20年时间段(1998年至2017年)内各经济体平均区域创新指数
$\left\langle {I} \right\rangle $ 与相对人均GDP的平均增长率$\left\langle {\Delta g} \right\rangle $ 之间的相关性 (a)$Z=\left\langle {I} \right\rangle^{\beta} $ , 其中β = 3.80为相关性最强时所对应β值, 直线为拟合直线; 插图显示为$\left\langle {I} \right\rangle $ 同$\left\langle {\Delta g} \right\rangle $ 之间的相关性(即设定β = 1.0时); (b) 通过相对人均GDP进行修正后的相关性,$Z_{\rm f}=\left\langle { I} \right\rangle^{\beta}+(a\left\langle { g} \right\rangle ^2+b\left\langle { g} \right\rangle +c)/k $ , 其中$\left\langle { g} \right\rangle $ 为各经济体的相对人均GDP的对数值g的20年均值, 其中β = 3.80, a = -0.011, b = –0.020, c = 0.0013, 而k = 0.033为图(a)的拟合直线斜率; 插图显示了修正函数$f(\left\langle { g} \right\rangle)=a\left\langle { g} \right\rangle^2+b\left\langle { g} \right\rangle+c$ 的获得, 即对图(a)的回归残差ε同$\left\langle {g} \right\rangle $ 的关系进行拟合所得Figure 4. The correlations between the average regional innovation index of each country
$\left\langle {I} \right\rangle $ and the average growth rate of relative per capita GDP$ \left\langle {\Delta g} \right\rangle $ in the period from 1998 to 2017: (a)$ Z=\left\langle {I} \right\rangle^{\beta} $ , where β = 3.80 corresponding to the strongest correlation between$\left\langle {\Delta g} \right\rangle $ and Z, and the dashed line is the fitting line. The inset of panel (a) shows the correlation between$\left\langle {I} \right\rangle $ and$\left\langle {\Delta g} \right\rangle $ (setting β = 1.0); (b) the correlation between$\left\langle {\Delta g} \right\rangle $ and the corrected prediction value Zf of each economy, where$Z_{\rm f}=\left\langle { I} \right\rangle^{\beta}+(a\left\langle { g} \right\rangle ^2+b\left\langle { g} \right\rangle +c)/k $ ,$\left\langle { g} \right\rangle $ is the 20-year average of the logarithmic relative GDP per capita g of each economy, and β = 3.80, a = -0.011, b = –0.020, c = 0.0013, and k = 0.033 is the slope of the fitting line in Fig.(a). The dashed line in the inset of Fig. (b) shows the correction function$f(\left\langle { g} \right\rangle)=a\left\langle { g} \right\rangle^2+b\left\langle { g} \right\rangle+c$ , which is obtained by the fitting for the correlation between ε and$\left\langle { g} \right\rangle $ , where ε is the regression residuals in the linear regression shown in Fig. (a)图 5 以1年期、3年期和5年期为滑动窗口长度, 各类指标在滑动窗口期内各经济体的均值同相对人均GDP增长率的平均值
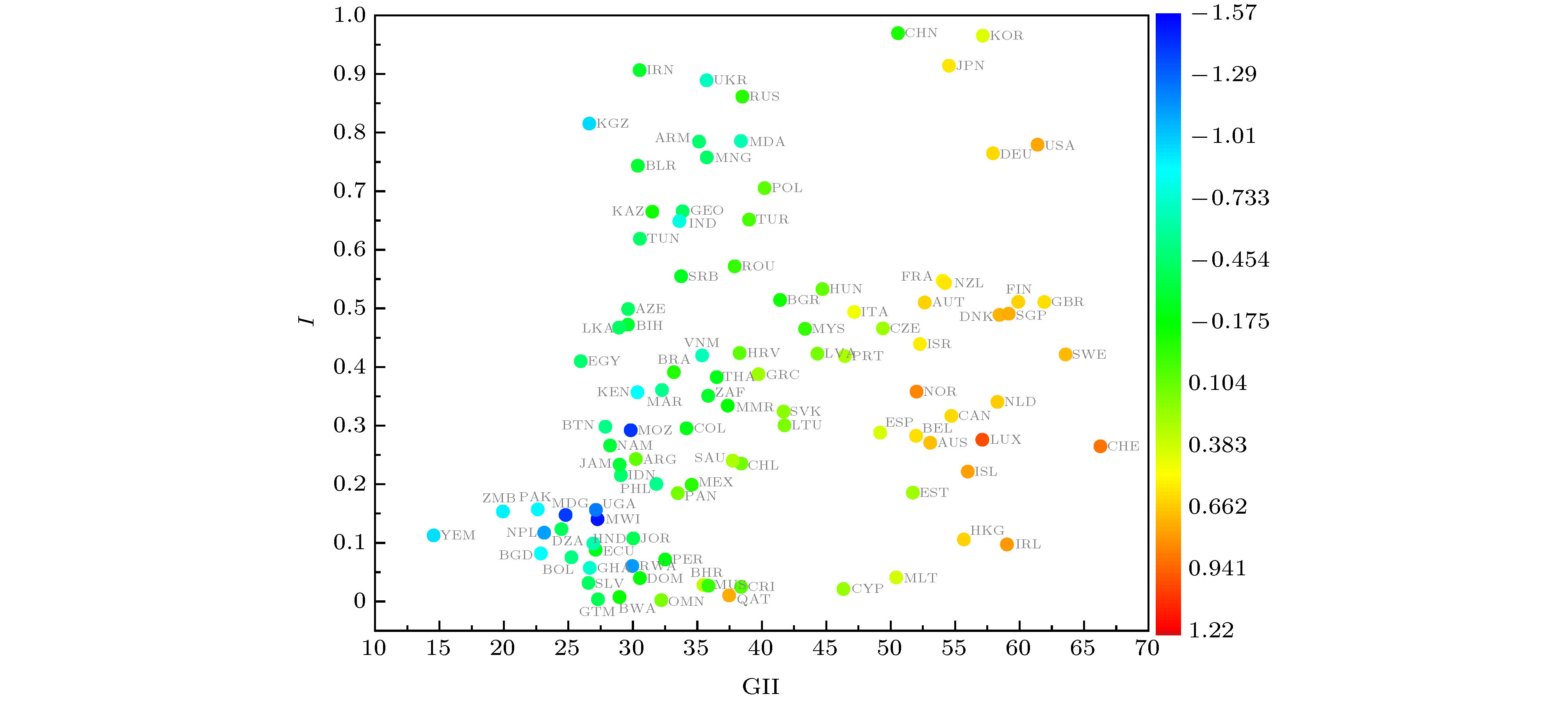
$\left\langle {\Delta g} \right\rangle $ 之间的相关性随年份的变化. 黑色、蓝色和粉色实线及其空心数据点对应指标为创新指数(该相关性表示为rI); 其中不同灰度的虚线标志出相关性rI在最低限度情况下(即有效数据点最少的情况, 对应滑动窗口长度为1年时)的不同显著性水平的边界, 浅灰、中灰和深灰虚线分别对应P = 0.05, 0.01, 0.001的rI值. 深黄、深青色、品红虚线及其实心数据点对应指标为全球创新指数GII(该相关性表示为rGII). 橄榄绿色虚线及其空心数据点对应指标为相对人均专利申请数的对数值np(该相关性表示为rp, 只显示了滑动窗口为5年期的情况). 插图显示的是, 采用5年期滑动窗口, 高收入经济体的相对人均GDP的平均增长率$\left\langle {\Delta g} \right\rangle _{\rm H} $ 与所有经济体的相对人均GDP增长率的均值$\left\langle {\Delta g} \right\rangle_{\rm W} $ 的差值$\left(\left\langle {\Delta g} \right\rangle_{\rm H}- \left\langle {\Delta g} \right\rangle_{\rm W}\right) $ , 同相关性rI(粉色点)和相关性rp(橄榄绿色点)的相关性; 实线分别为同色数据点的拟合直线Figure 5. Designing the moving window length of 1 year, 3 years and 5 years, for given index, the correlation between the average value of the index of each economy and the average growth rate
$\left\langle {\Delta g} \right\rangle $ of the relative GDP per capita within the moving window are shown by curves and data points. The black, blue and pink lines and hollow data points show correlation rI, corresponding to the index I. The different gray dashed lines show the thresholds of the correlation rI for different level of significance in the case with the minimum data points (corresponding to the case with 1-year moving window length), and the light gray, medium gray and dark gray dashed lines correspond to the significance P = 0.05, 0.01 and 0.001, respectively. The dark yellow, dark cyan, magenta dashed lines and solid data points show correlation rGII, corresponding to global innovation index (GII). The olive dashed line and hollow data points show correlation rp, corresponding to the index of the logarithmic relative number of patent applications per capita (np) (5-year-moving-window only). The inset shows the correlations between$\left(\left\langle {\Delta g} \right\rangle_{\rm H}- \left\langle {\Delta g} \right\rangle_{\rm W}\right) $ and rI, and the correlation beween$\left(\left\langle {\Delta g} \right\rangle_{\rm H}- \left\langle {\Delta g} \right\rangle_{\rm W}\right) $ and rp, where$\left\langle {\Delta g} \right\rangle_{\rm H} $ and$ \left\langle {\Delta g} \right\rangle_{\rm W} $ is the average growth rate of the relative GDP per capita within the moving window for high-income economies and all economies, respectively, and the solid lines respectively are the fitting curve for the data points with the same color.图 6 (a)和(b)分别对比了在谷-峰变换和峰-谷变换前后的两个典型年份的5年滑动窗口内各经济体的创新指数
$\left\langle {I} \right\rangle $ 的平均值与相对人均GDP增长率$\left\langle {\Delta g} \right\rangle $ 的平均值之间的相关性. (a) 青色六角圈对应1994年(rI值谷值), 桃红色圆点对应2004年(rI值峰值), 同一经济体由灰色线连接, 绿色虚线和桃红色虚线分别为1994年和2004年数据点的拟合直线, 斜率分别为–0.050和0.073; (b) 桃红色圈和蓝色圆点分别对应2004年(rI值峰值)和2014年(rI值谷值)的数据点, 同一经济体由灰色线连接, 桃红色虚线(斜率0.073)和蓝色虚线(斜率–0.033)分别为2004年和2014年数据点的拟合直线; (c) 1994年至2004年的谷-峰变换中各国的$\left\langle {\Delta g} \right\rangle $ 改变量$\left(\left\langle {\Delta g} \right\rangle_{2004} - \left\langle {\Delta g} \right\rangle_{1994}\right) $ 同2004年至2014年的峰-谷变换中各经济体的$ \left\langle {\Delta g} \right\rangle $ 改变量$\left(\left\langle {\Delta g} \right\rangle_{2014} - \left\langle {\Delta g} \right\rangle_{2004}\right) $ 的关系, 其中各数据点的直径正比于该经济体自1995至2014年间的创新指数I的20年平均值, 颜色对应于该期间各经济体的相对人均GDP增长率Δg的20年平均值, 虚线为拟合直线Figure 6. (a) and (b) respectively compare the correlations between the average value of the index I of each economy
$\left\langle {I} \right\rangle $ and the average growth rate$\left\langle {\Delta g} \right\rangle $ of the relative GDP per capita at the 5-year moving windows before and after the transition from bottom on rI wave to peak and the one from peak to bottom. Fig. (a) shows the comparison between 1994 (the cyan hexagons, at the bottom) and 2004 (the pink dots, at the peak), where the data points of the same economy are connected by gray lines, and the green dashed line and the pink dashed line respectively show the linear fittings of 1994 (with a slope of –0.050) and the one of 2004 (with a slope of 0.073); Fig. (b) shows the comparison between 2004 (the pink circles, at the peak) and 2014 (the blue dots, at the valley), where the data points of the same economy are connected by gray lines, and the pink dashed line (with a slope 0.073) and the blue dashed line (with a slope of –0.033) show the linear fittings of 2004 and 2014, respectively; Panel (c) plots the relationship between the change$\left(\left\langle {\Delta g} \right\rangle_{2004} - \left\langle {\Delta g} \right\rangle_{1994}\right)$ in the valley-peak transition and the change$\left(\left\langle {\Delta g} \right\rangle_{2014}-\left\langle {\Delta g} \right\rangle_{2004}\right) $ in the peak-valley transition, where the diameter of each circle is proportional to the 20 year average$\left\langle {I} \right\rangle $ of the economy’s index, and the color corresponds to the 20-year average growth rate$\left\langle {\Delta g} \right\rangle $ of the economy’s relative GDP per capita.表 A1 148个经济体在2016年的区域创新指数I值
Table A1. The index I of 148 economies at 2016.
排序 经济体名称 英文名称 2016年指数I 排序 经济体名称 英文名称 2016年指数I 1 中国大陆地区 Mainland China 0.969 75 墨西哥 Mexico 0.199 2 韩国 Republic of Korea 0.965 76 爱沙尼亚 Estonia 0.185 3 日本 Japan 0.914 77 巴拿马 Panama 0.185 4 伊朗伊斯兰共和国 Islamic Republic of Iran 0.906 78 巴基斯坦 Pakistan 0.157 5 乌克兰 Ukraine 0.889 79 乌干达 Uganda 0.156 6 俄罗斯联邦 The Russian Federation 0.861 80 赞比亚 Zambia 0.153 7 吉尔吉斯斯坦 Kyrgyzstan 0.815 81 马达加斯加 Madagascar 0.147 8 摩尔多瓦 Moldova 0.786 82 马拉维 Malawi 0.140 9 亚美尼亚 Armenia 0.784 83 摩纳哥 Monaco 0.131 10 美国 USA 0.779 84 阿尔及利亚 Algeria 0.123 11 德国 Germany 0.764 85 尼泊尔 Nepal 0.117 12 蒙古 Mongolia 0.758 86 也门共和国 Republic of Yemen 0.112 13 白俄罗斯 Belarus 0.743 87 约旦 Jordan 0.108 14 波兰 Poland 0.705 88 中国香港特别行政区 Hong Kong of China 0.106 15 格鲁吉亚 Georgia 0.666 89 洪都拉斯 Honduras 0.099 16 哈萨克斯坦 Kazakhstan 0.665 90 爱尔兰 Ireland 0.097 17 土耳其 Turkey 0.651 91 津巴布韦 Zimbabwe 0.089 18 印度 India 0.649 92 厄瓜多尔 Ecuador 0.088 19 突尼斯 Tunisia 0.619 93 孟加拉国 Bangladesh 0.082 20 罗马尼亚 Romania 0.572 94 玻利维亚 Bolivia 0.075 21 乌兹别克斯坦 Uzbekistan 0.556 95 秘鲁 Peru 0.071 22 塞尔维亚 Serbia 0.555 96 古巴 Cuba 0.068 23 法国 France 0.547 97 卢旺达 Rwanda 0.060 24 新西兰 new Zealand 0.543 98 加纳 Ghana 0.057 25 匈牙利 Hungary 0.533 99 马耳他 Malta 0.041 26 保加利亚 Bulgaria 0.514 100 多米尼加共和国 Dominican Republic 0.040 27 芬兰 Finland 0.511 101 巴哈马 Bahamas 0.039 28 英国 Britain 0.511 102 萨尔瓦多 El Salvador 0.032 29 奥地利 Austria 0.510 103 巴林 Bahrain 0.028 30 阿塞拜疆 Azerbaijan 0.499 104 毛里求斯 Mauritius 0.026 31 意大利 Italy 0.494 105 哥斯达黎加 Costa Rica 0.025 32 新加坡 Singapore 0.491 106 塞浦路斯 Cyprus 0.021 33 丹麦 Denmark 0.489 107 特立尼达和多巴哥 Trinidad and Tobago 0.019 34 波斯尼亚和黑塞哥维那 Bosnia and Herzegovina 0.472 108 卡塔尔 Qatar 0.010 35 斯里兰卡 Sri Lanka 0.467 109 博茨瓦纳 Botswana 0.007 36 捷克共和国 Czech Republic 0.466 110 危地马拉 Guatemala 0.003 37 马来西亚 Malaysia 0.465 111 阿曼 Oman 0.002 38 苏丹 Sudan 0.441 —— 阿鲁巴 Aruba —— 39 以色列 Israel 0.439 —— 安哥拉 Angola —— 40 克罗地亚 Croatia 0.424 —— 阿尔巴尼亚 Albania —— 41 拉脱维亚 Latvia 0.423 —— 阿拉伯联合酋长国 United Arab Emirates —— 42 瑞典 Sweden 0.421 —— 布隆迪 Burundi —— 43 越南 Vietnam 0.420 —— 布基纳法索 Burkina Faso —— 44 葡萄牙 Portugal 0.419 —— 伯利兹 Belize —— 45 阿拉伯埃及共和国 Arab Republic of Egypt 0.410 —— 巴巴多斯 Barbados —— 46 巴西 Brazil 0.391 —— 文莱达鲁萨兰国 Brunei Darussalam —— 47 希腊 Greece 0.387 —— 科特迪瓦 Ivory Coast —— 48 泰国 Thailand 0.383 —— 刚果(金) The Democratic Republic of Congo —— 49 摩洛哥 Morocco 0.361 —— 刚果(布) The Republic of Congo —— 50 挪威 Norway 0.358 —— 吉布提 Djibouti —— 51 肯尼亚 Kenya 0.357 —— 埃塞俄比亚 Ethiopia —— 52 南非 South Africa 0.351 —— 斐济 Fiji —— 53 荷兰 Netherlands 0.340 —— 圭亚那 Guyana —— 54 黑山 Montenegro 0.334 —— 海地 Haiti —— 55 斯洛伐克共和国 Slovak Republic 0.324 —— 伊拉克 Iraq —— 56 加拿大 Canada 0.316 —— 柬埔寨 Cambodia —— 57 圣马力诺 San Marino 0.305 —— 黎巴嫩 Lebanon —— 58 立陶宛 Lithuania 0.300 —— 利比亚 Libya —— 59 不丹 Bhutan 0.298 —— 莱索托 Lesotho —— 60 哥伦比亚 Colombia 0.295 —— 中国澳门特别行政区 Macau of China —— 61 莫桑比克 Mozambique 0.292 —— 北马其顿 North Macedonia —— 62 西班牙 Spain 0.288 —— 马里 Mali —— 63 比利时 Belgium 0.283 —— 尼日利亚 Nigeria —— 64 卢森堡 Luxembourg 0.276 —— 尼加拉瓜 Nicaragua —— 65 澳大利亚 Australia 0.271 —— 巴布亚新几内亚 Papua New Guinea —— 66 纳米比亚 Namibia 0.266 —— 巴拉圭 Paraguay —— 67 瑞士 Switzerland 0.265 —— 斯洛文尼亚 Slovenia —— 68 阿根廷 Argentina 0.243 —— 阿拉伯叙利亚共和国 Syrian Arab Republic —— 69 沙特阿拉伯 Saudi Arabia 0.240 —— 塔吉克斯坦 Tajikistan —— 70 智利 Chile 0.235 —— 土库曼斯坦 Turkmenistan —— 71 牙买加 Jamaica 0.233 —— 坦桑尼亚 Tanzania —— 72 冰岛 Iceland 0.221 —— 乌拉圭 Uruguay —— 73 印度尼西亚 Indonesia 0.215 —— 委内瑞拉玻利瓦尔共和国 Bolivarian Republic of Venezuela —— 74 菲律宾 Philippines 0.200 —— 萨摩亚 Samoa —— 注: “——”说明该年份的该经济体的数据缺失, 相应也没有其排序序号. -
[1] Hansen T, Winther L 2011 Eur. Urban Reg. Stud. 18 321
 Google Scholar
Google Scholar
[2] Fagerberg J E, Srholec M 2008 Res. Policy 37 1417
 Google Scholar
Google Scholar
[3] Wignaraja G 2012 J. Asian Econ. 23 224
 Google Scholar
Google Scholar
[4] Mohnen P, Dagenais M 2002 Towards an Innovation Intensity Index: The Case of CIS 1 in Denmark and Ireland In: Innovation and Firm Performance (London: Kleinknecht A, Mohnen P, eds.) pp3–30
[5] Slaper T F, Hart N R, Hall T J, Thompson M F 2011 Econ. Dev. Q. 25 36
 Google Scholar
Google Scholar
[6] Clayton T, Borgo M D, Haskel J 2009 https://ssrn.com/ abstract=1345684
[7] Żelazny R, Pietrucha J 2017 Q. J. Econ. Econ. Policy 12 43
[8] Crespo N F, Crespo C F 2016 J. Bus. Res. 69 5265
 Google Scholar
Google Scholar
[9] Sohn S Y, Kim D H, Jeon S Y 2016 Technol. Anal. Strateg. Manag. 28 492
 Google Scholar
Google Scholar
[10] McGrath M E, Romeri M N 1994 J. Prod. Innov. Manag. 11 213
 Google Scholar
Google Scholar
[11] Narin F, Olivastro D 1988 Technology Indicators Based On Patents And Patent Citations In: Handbook of Quantitative Studies of Science and Technology (Amsterdam: Van Raan A F J, eds.) pp465–507
[12] Guan J C, Gao X 2009 J. Associat. Inf. Sci. Technol. 60 35
 Google Scholar
Google Scholar
[13] Csajbók E, Berhidi A, Vasas L, et al. 2007 Scientometrics 73 91
 Google Scholar
Google Scholar
[14] Mester G 2016 Interdiscipl. Descript. Compl. Syst. 14 1
 Google Scholar
Google Scholar
[15] Gao H 2014 Internat. J. Adv. Manag. Sci. 3 128
 Google Scholar
Google Scholar
[16] May M, Brody H 2015 Nature 522 S1
 Google Scholar
Google Scholar
[17] Haunschild R, Bornmann L 2015 Scientometrics 102 1829
 Google Scholar
Google Scholar
[18] 中国区域创新指数报告课题组 2019 中国西部 2019 19
 Google Scholar
Google Scholar
Report of China Regional Innovation Index Research Group 2019 Western China 2019 19
 Google Scholar
Google Scholar
[19] Bettencourt L M A, Lobo J, Helbing D, Kühnert C, West G B 2007 Proc. Natl. Acad. Sci. U. S. A. 104 7301
 Google Scholar
Google Scholar
[20] Bettencourt L M A, West G B 2010 Nature 467 912
 Google Scholar
Google Scholar
[21] Arbesman S, Kleinberg J M, Strogatz S H 2009 Phys. Rev. E 79 16115
 Google Scholar
Google Scholar
[22] Wunsch-Vincent S, Lanvin B, Dutta S 2015 eSocialSciences Working Paper id: 7491
[23] Hirooka M 2003 J. Evol. Econ. 13 549
 Google Scholar
Google Scholar
[24] Groot B de, Franses P H 2009 Technol. Forecast. Social Chang. 76 1021
 Google Scholar
Google Scholar
[25] Hausman A, Johnston W J 2014 J. Bus. Res. 67 2720
 Google Scholar
Google Scholar
[26] Gao J, Zhang Y C, Zhou T 2019 Phys. Rep. 817 1
 Google Scholar
Google Scholar
[27] Hidalgo C A, Klinger B, Barabási A L, Hausmann R 2007 Science 317 482
 Google Scholar
Google Scholar
[28] Hidalgo C A, Hausmann R 2009 Proc. Natl. Acad. Sci. U.S.A. 106 10570
 Google Scholar
Google Scholar
[29] Caldarelli G, Cristelli M, Gabrielli A, Pietronero L, Scala A, Tacchella A 2012 PLoS ONE 7 e47278
 Google Scholar
Google Scholar
[30] Cristelli M, Gabrielli A, Tacchella A, Caldarelli G, Pietronero L 2013 PLoS ONE 8 e70726
 Google Scholar
Google Scholar
[31] Neffke F, Henning M, Boschma R 2011 Econ. Geogr. 87 237
 Google Scholar
Google Scholar
[32] Tacchella A, Mazzilli D, Pietronero L 2018 Nat. Phys. 14 861
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 11837
- PDF Downloads: 174
- Cited By: 0














 DownLoad:
DownLoad: