-
Relaxation oscillations are ubiquitous in various fields of natural science and engineering technology. Exploring possible routes to relaxation oscillations is one of the important issues in the study of relaxation oscillations. Recently, the pulse-shaped explosion (PSE), a novel mechanism which can lead to relaxation oscillations, has been reported. The PSE means pulse-shaped sharp quantitative changes related the variation of system parameters in branches of equilibrium points and limit cycles, which leads the system’s trajectory to undertake sharp transitions and further induces relaxation oscillations. Regarding externally and parametrically excited nonlinear systems with different frequency ratios, some work on PSE has been reported. The present paper focuses on the PSE and the related relaxation oscillations in a externally and parametrically excited Mathieu-van der Pol-Duffing system. We show that if there is an initial phase difference between the slow excitations with the same frequency ratio, the fast subsystem may compose of two parts with different expressions, each of which determines a different vector field. As a result, the bistable behaviors are observed in the system. In particular, one of the vector fields exhibits two groups of bifurcation behaviors, which are symmetric with respect to the positive and negative PSE, and each can induce a cluster in the relaxation oscillations. Based on this, we present several routes to compound relaxation oscillations, and obtain new types of relaxation oscillations connected by pulse-shaped explosion, which we call compound “subHopf/fold-cycle” relaxation oscillations and compound “supHopf/supHopf” relaxation oscillations, respectively. Our results show that the two clusters in the resultant relaxation oscillations are connected by the PSE, and the initial phase difference plays an important role in transitions to different attractors and the generation of relaxation oscillations. Although the research in this paper is based on a specific nonlinear system, we would like to point out that the bistable behaviors, the PSE and the resultant compound relaxation oscillations can also be observed in other dynamical systems. The reason is that the fast subsystem composes of two different vector fields induced by the initial phase difference, which dose not rely on a specific system. The results of this paper deepen the research about PSE as well as the complex dynamics of relaxation oscillations.
-
Keywords:
- relaxation oscillations /
- pulse-shaped explosion /
- frequency conversion fast-slow analysis /
- multi-frequency excitations /
- bifurcation mechanism
[1] Belhaq M, Ghouli Z, Hamdi M 2018 Nonlinear Dyn. 94 2537
Google Scholar
[2] Mani A K, Narayanan M D, Sen M 2018 Nonlinear Dyn. 93 945
Google Scholar
[3] Miwadinou C H, Hinvi L A, Monwanou A V, Orou J B C 2017 Nonlinear Dyn. 88 97
Google Scholar
[4] Miwadinou C H, Monwanou A V, Yovogan J, Hinvi L A, Tuwa P R N, Orou J B C 2018 Chin. J. Phys. 56 1089
Google Scholar
[5] 于文婷, 张娟, 唐军 2017 66 200201
Google Scholar
Yu W T, Zhang J, Tang J 2017 Acta Phys. Sin. 66 200201
Google Scholar
[6] Ferraro M, D'annessa I, Moroni E, Morra G, Paladino A, Rinaldi S, Compostella, F, Colombo G 2019 J. Med. Chem. 62 60
Google Scholar
[7] 谢献忠, 沈伟成, 彭剑, 龙昊 2016 防灾减灾工程学报 36 972
XieX Z, Sheng W C, Peng J, Long H 2016 Journal of Disaster Prevention and Mitigation Engineering 36 972
[8] Tuttle T D, Seering W P 1996 IEEE Trans. Rob. Autom. 12 368
Google Scholar
[9] 梁晓冰, 刘希顺, 刘安芝, 王博亮 2009 58 5065
Google Scholar
Liang X B, Liu X S, Liu A Z, Wang B L 2009 Acta Phys. Sin. 58 5065
Google Scholar
[10] Li Y X, Rinzel J 1994 J. Theor. Biol. 166 461
Google Scholar
[11] Newby J M, Bressloff P C, Keener J P 2013 Phys. Rev. Lett. 111 128101
Google Scholar
[12] Zhang J J, Chen D Y, Zhang H, Xu B B, Li H H, Aggidis G A, Chatterton S 2019 J. Vib. Control 25 2863
Google Scholar
[13] He J H, Ji F Y 2019 Therm. Sci. 23 2131
Google Scholar
[14] Deng B 2004 Chaos 14 1083
Google Scholar
[15] Roberts A 2016 SIAM J. Appl.Dyn. Syst. 15 609
Google Scholar
[16] Krupa M, Touboul J D 2016 J. Dyn. Differ. Equ. 28 471
Google Scholar
[17] Golmakani A, Homburg A J 2011 Dynam Syst. 26 61
Google Scholar
[18] Cheng W, Xiang Z 2019 J. Differ. Equ. 267 3397
Google Scholar
[19] Nikolay D D, Stepan A T 2019 Appl. Math. Lett. 96 208
Google Scholar
[20] LI JZ, Tomsovic S 2019 Phys. Rev. E 99 032212
Google Scholar
[21] Han X J, Xia F B, Ji P, Bi Q S, Kurths J 2016 Commun. Nonlinear Sci. Numer. Simul. 36 517
Google Scholar
[22] Cao J D, Guerrini L, Cheng Z S 2019 Appl. Math. Comput. 343 21
[23] Li L, Wang Z, Li Y X, Shen H, Lu J W 2018 Appl. Math. Comput. 330 152
[24] Han M A, Zhang W N 2010 J. Differ. Equ. 248 2399
Google Scholar
[25] Jiang H P, Zhang T H, Song Y L 2015 Int. J. Bifurcation Chaos 25 1550058
Google Scholar
[26] Monica C, PItchaimani M 2016 Nonlinear Anal. Real World Appl. 27 55
Google Scholar
[27] Wang Z, Wang X H, Li Y X, Huang X 2017 Int. J. Bifurcation Chaos 27 1750209
Google Scholar
[28] 魏梦可, 韩修静, 张晓芳, 毕勤胜 2019 力学学报 51 904
Google Scholar
Wei M k, Han X J, Zhang X F, Bi Q S 2019 Chinese Journal of Theoretical and Applied Mechanics 51 904
Google Scholar
[29] Han X J, Bi Q S, Kurths J 2018 Phys. Rev. E 98 010201
Google Scholar
[30] Mohamad M A, Sapsis T P 2016 Ocean Eng. 120 289
Google Scholar
[31] Lakrad F, Azouani A, Abouhazim N, Belhaq M 2005 Chaos, Solitons Fractals 24 813
Google Scholar
[32] Wiggers V, Rech P C 2018 Eur. Phys. J. B 91 144
Google Scholar
[33] Shukla A K, Ramamohan T R, Srinivas S 2014 Phys. Scr. 89 075202
Google Scholar
[34] Kumar P, Kumar A, Erlicher S 2017 Physica D 358 1
Google Scholar
[35] Tamba V K, Kingni S T, Kuiate G F, Fotsin H B, Talla P K 2018 Pramana-J Phys. 91 12
Google Scholar
[36] He J H 2005 Chaos, Solitons Fractals 26 695
Google Scholar
[37] He J H 1999 Int. J. NonLinear Mech. 34 699
Google Scholar
[38] He J H, Abdou M A 2007 Chaos, Solitons Fractals 34 1421
Google Scholar
[39] He J H 2019 Results in Physics 15 102546
Google Scholar
[40] Li Y J, Wu Z Q, Wang F, Zhang G Q, Wang Y C 2019 J. Low Freq. Noise Vib. Act. Control UNSP 1461348419878534
[41] He J H 2014 Indian J. Phys. 88 193
Google Scholar
[42] Han X J, Bi Q.S, Ji P, Kurths J 2015 Phys. Rev. E 92 012911
Google Scholar
[43] Sprott J C, Li C B 2014 Phys. Rev. E 89 066901
Google Scholar
[44] Arumugam R, Sarkar S, Banerjee T, Sinha S, Dutta P S 2019 Phys. Rev. E 99 012911
-
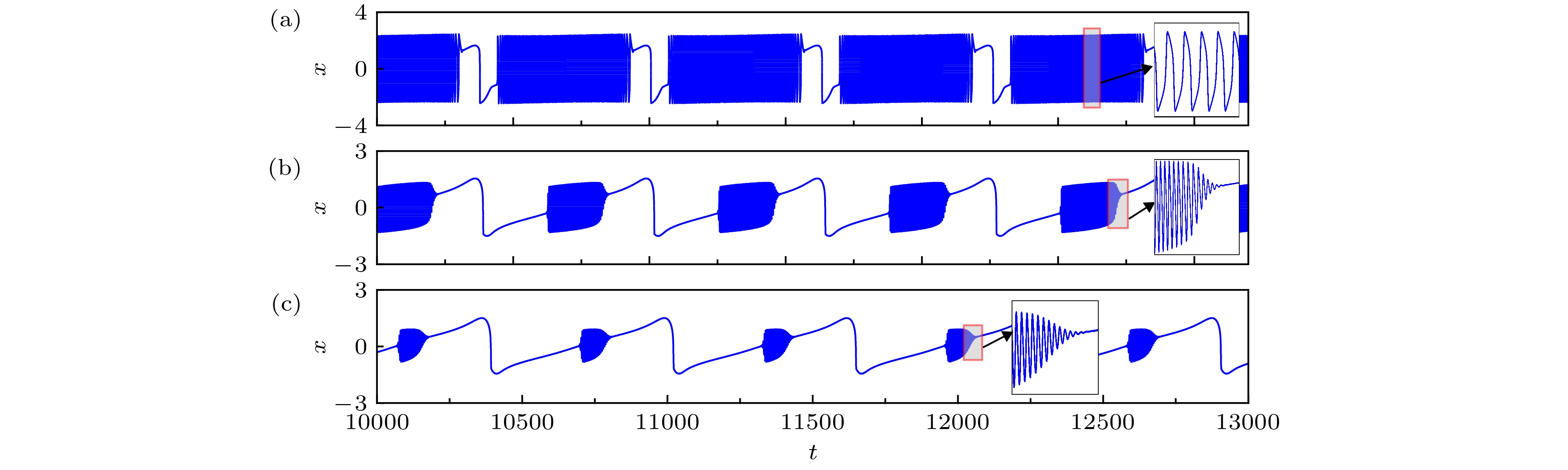
图 1 系统(1)中典型的复合式张弛振荡 (a)
$\alpha = 1.5$ ; (b)$\alpha = 0.4$ ; (c)$\alpha = 0.2$ . 其他参数固定在$\gamma = 4$ ,$\delta = 1.00$ ,${\beta _1} = 0.99$ ,${\beta _2} = 1$ ,$\omega = 0.01$ 和$\theta = - {{\text{π}}}/{2}$ Figure 1. Typical compound relaxation oscillations in system (1): (a)
$\alpha = 1.5$ ; (b)$\alpha = 0.4$ ; (c)$\alpha = 0.2$ . Other parameters are fixed at$\gamma = 4$ ,$\delta = 1$ ,${\beta _1} = 0.99$ ,${\beta _2} = 1$ ,$\omega = 0.01$ and$\theta = - {{\text{π}}}/{2}$ .
图 2 (a)子系统(2a)和(b)子系统(2b)在参数平面
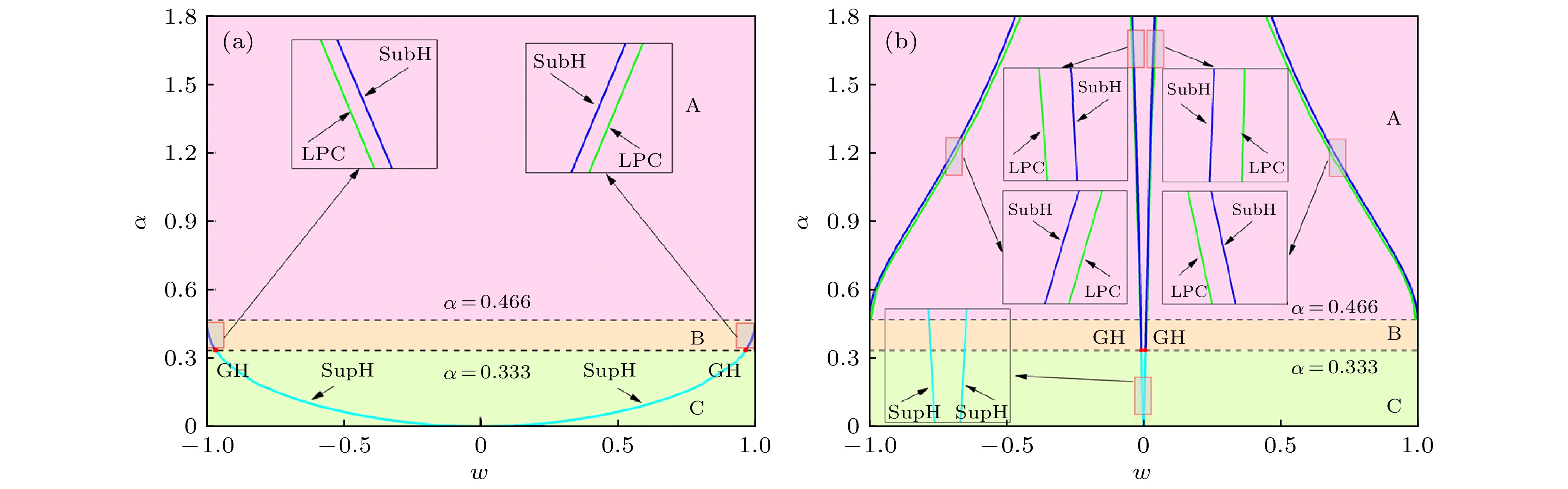
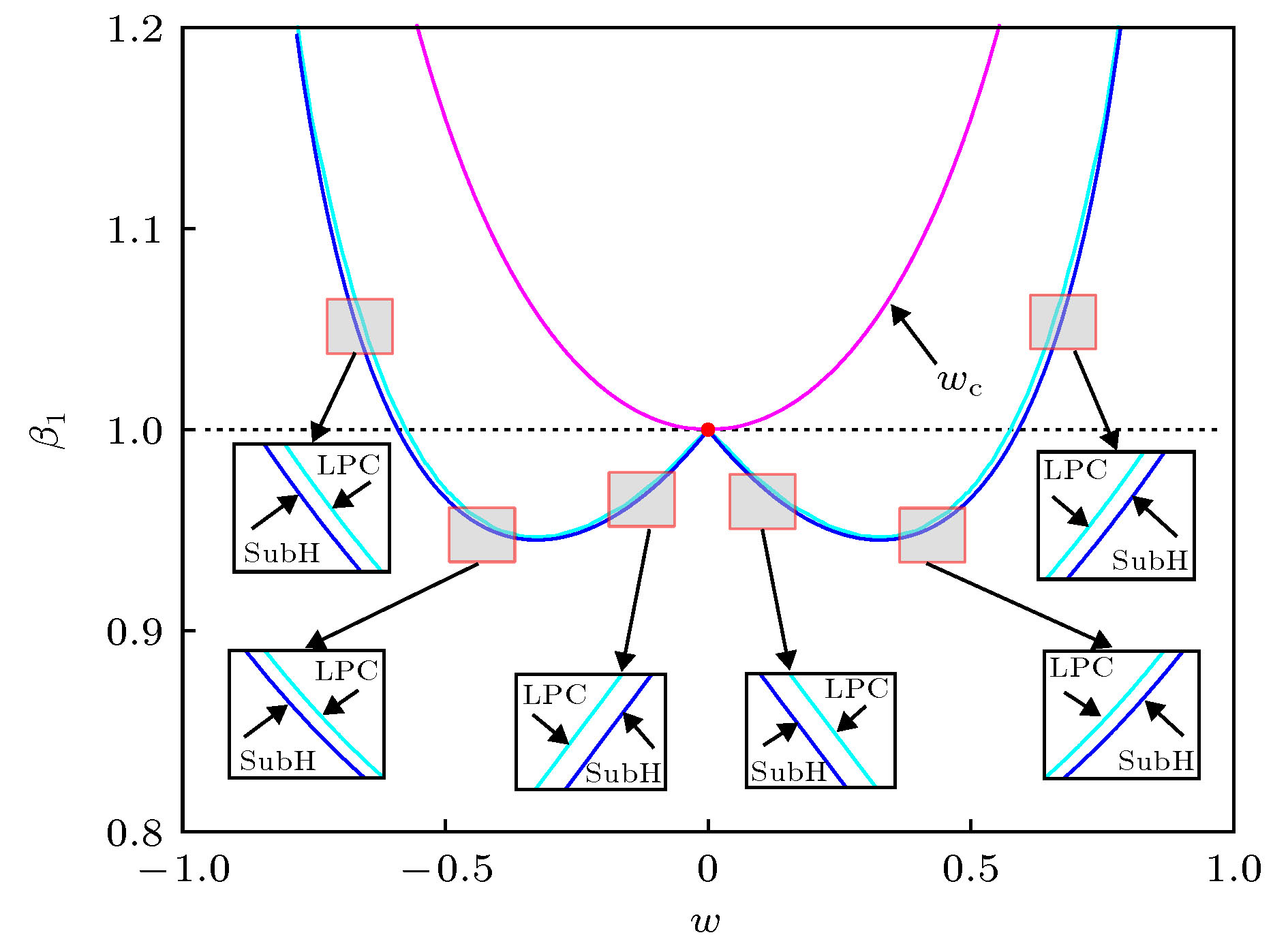
$(w, \alpha )$ 上的分岔集. 其中GH为广义Hopf分岔SubH为亚临界Hopf分岔, SupH为超临界Hopf分岔, LPC为极限环的分岔. 系统参数的取值与图1相同Figure 2. Bifurcation sets of the subsystem (2a) (a) and (2b) (b) in the parameter plane
$(w, \alpha )$ . Here GH represent the generalized Hopf bifurcation, SubH represent the subcritical Hopf bifurcation, SupH represent the supercritical Hopf bifurcation, LPC represent the limit point cycle bifurcation. The values of system parameters are the same as those in Fig. 1.
图 3 快子系统(2)在A, B, C各区域中典型的稳定性和分岔行为 (a1), (a2)
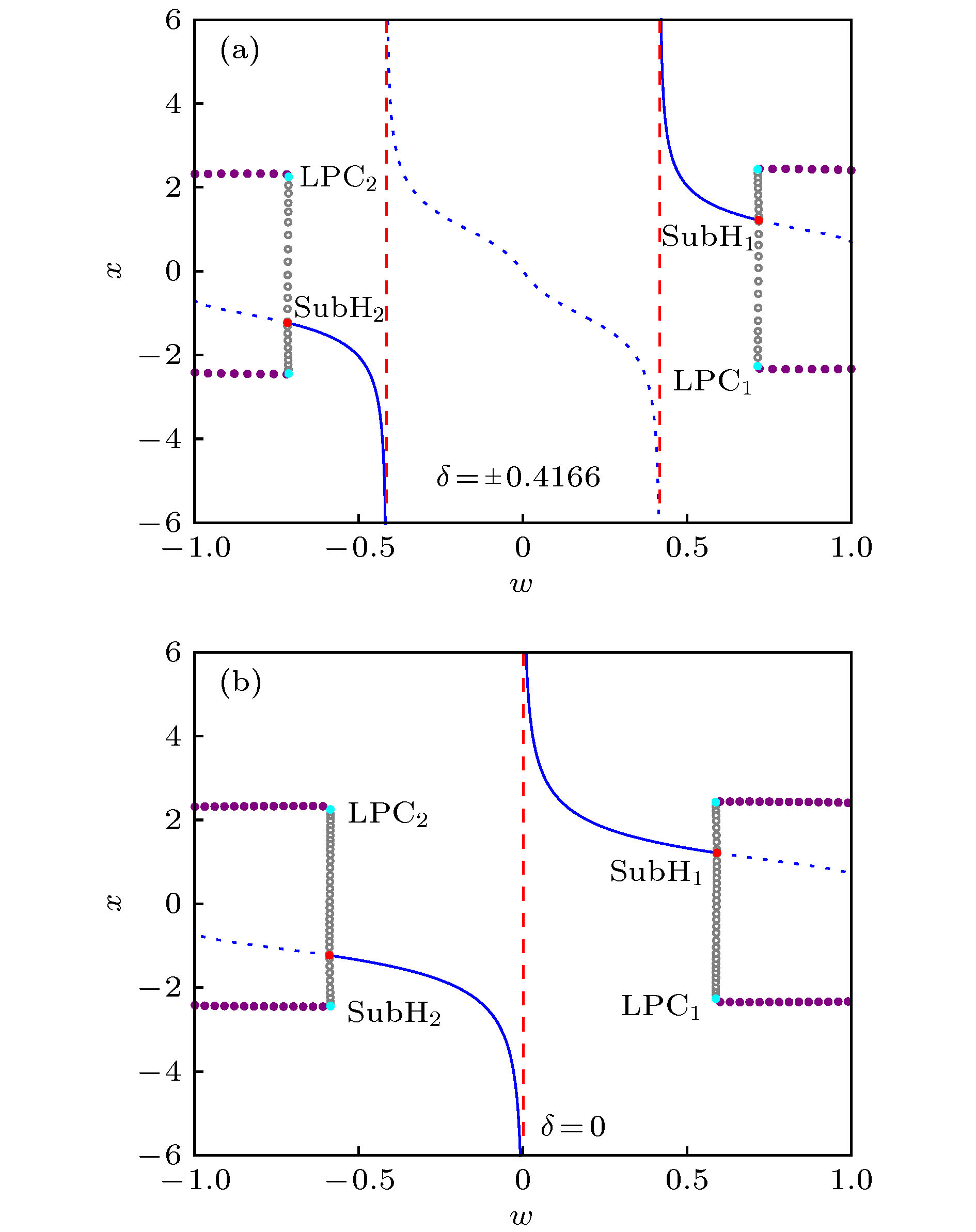
$\alpha = 1.5$ ; (b1), (b2)$\alpha = 0.4$ ; (c1), (c2)$\alpha = 0.2$ . 其他参数的取值与图1相同Figure 3. Typical stability and bifurcation behaviors of the fast subsystem (2) in the areas A, B and C: (a1), (a2)
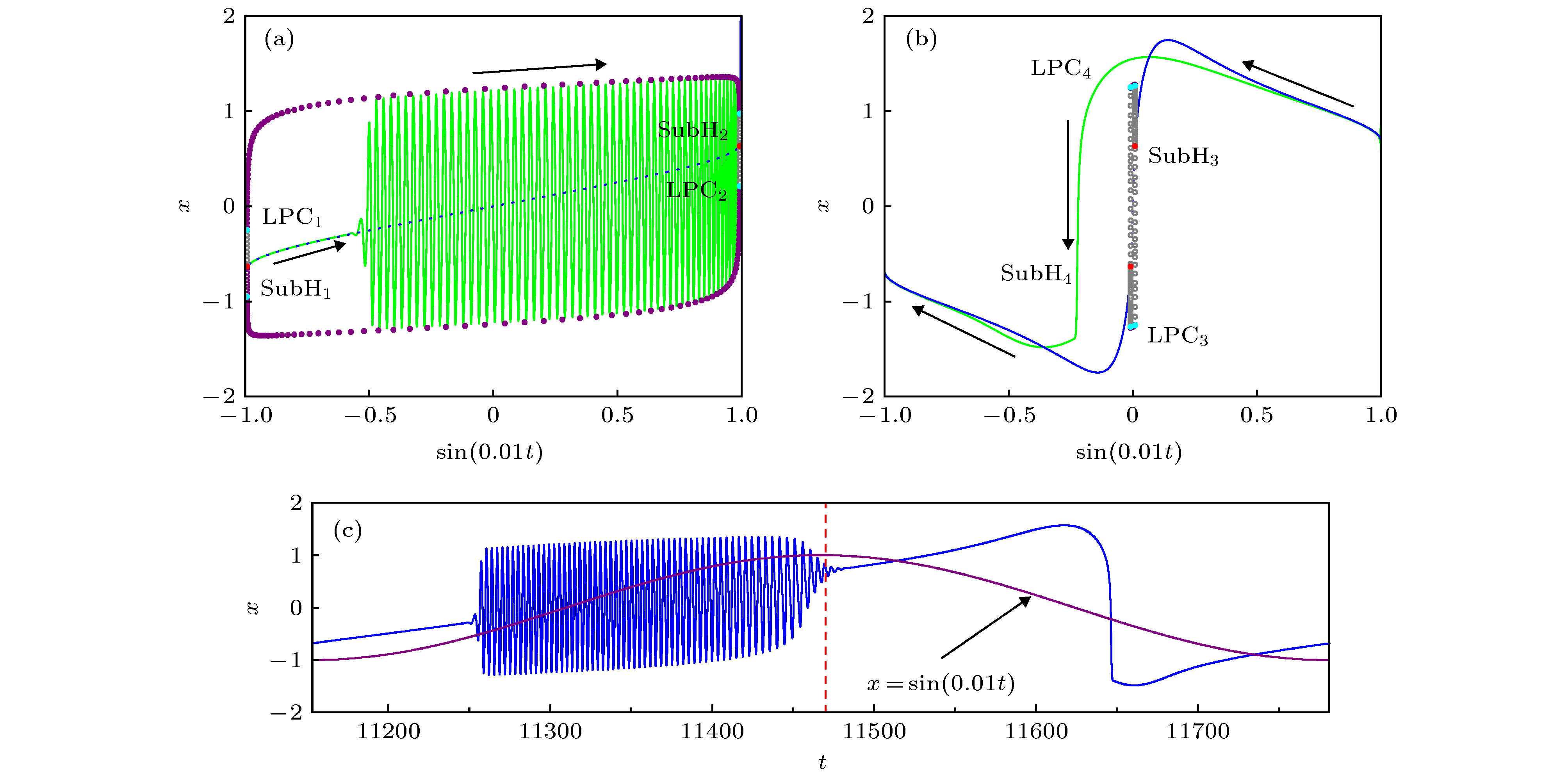
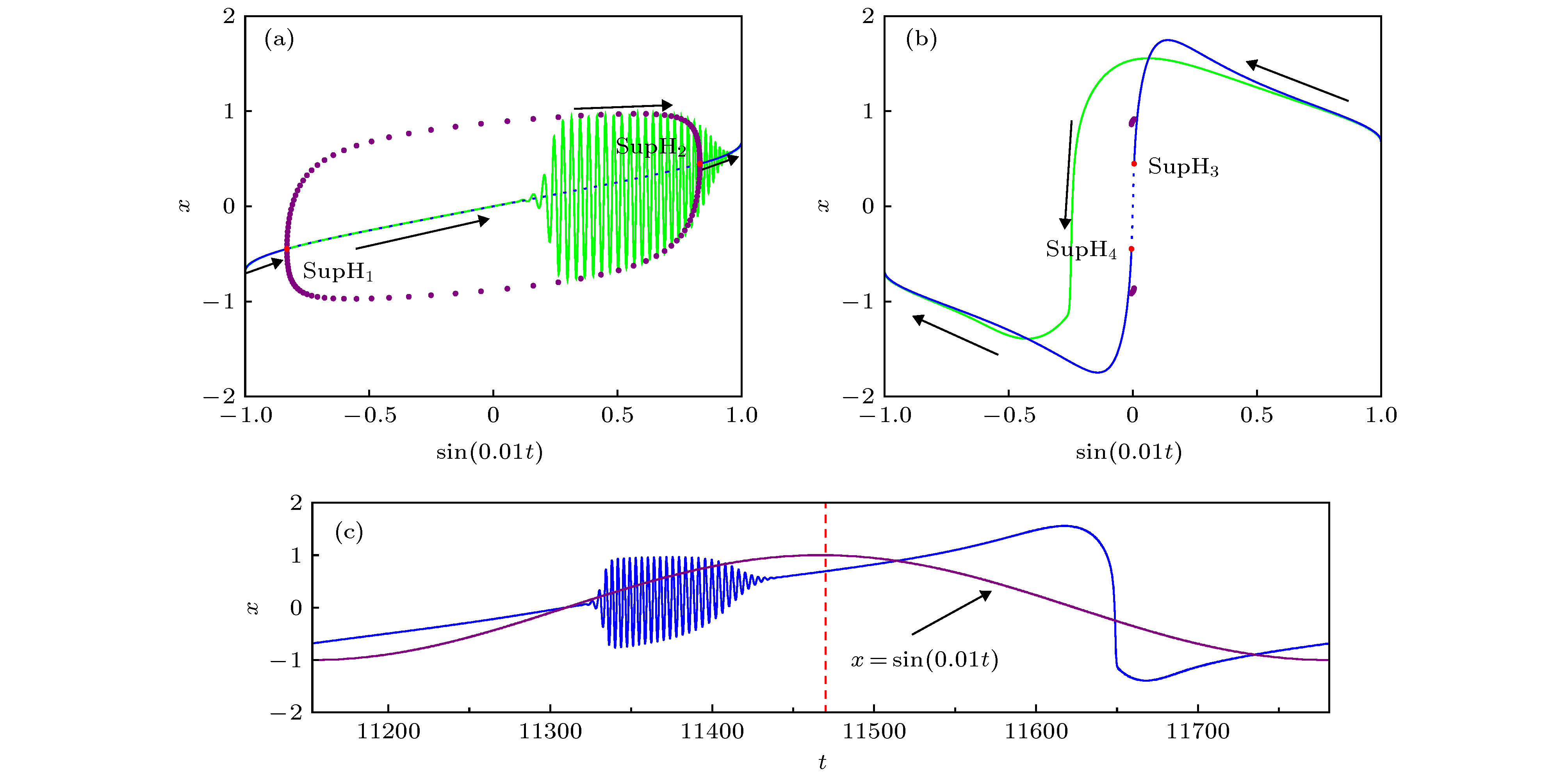
$\alpha = 1.5$ ; (b1), (b2)$\alpha = 0.4$ ; (c1), (c2)$\alpha = 0.2$ . The values of other parameters are the same as those in Fig. 1.
图 6 图1(a)中的张弛振荡的快慢分析 (a)张弛振荡的转换相图与图3(a1)中的分岔图的叠加(与子系统(2a)相关); (b)张弛振荡的转换相图与图3(a2)中分岔图的叠加(与子系统(2b)相关); (c)一个完整周期下的张弛振荡. 这里
$\alpha = 1.5$ , 而其他参数与图1相同Figure 6. Fast-slow analysis of the relaxation oscillations in Fig. 1(a): (a) Overlay of the transformed phase diagram of the relaxation oscillations and the bifurcation diagram in Fig. 3(a1) (related to the subsystem (2a)); (b) overlay of the transformed phase diagram of the relaxation oscillations and the bifurcation diagram in Fig. 3(a2) (related to the subsystem (2b)); (c) a whole period of the relaxation oscillations. Here
$\alpha = 1.5$ and other parameters are the same as those in Fig. 1. -
[1] Belhaq M, Ghouli Z, Hamdi M 2018 Nonlinear Dyn. 94 2537
Google Scholar
[2] Mani A K, Narayanan M D, Sen M 2018 Nonlinear Dyn. 93 945
Google Scholar
[3] Miwadinou C H, Hinvi L A, Monwanou A V, Orou J B C 2017 Nonlinear Dyn. 88 97
Google Scholar
[4] Miwadinou C H, Monwanou A V, Yovogan J, Hinvi L A, Tuwa P R N, Orou J B C 2018 Chin. J. Phys. 56 1089
Google Scholar
[5] 于文婷, 张娟, 唐军 2017 66 200201
Google Scholar
Yu W T, Zhang J, Tang J 2017 Acta Phys. Sin. 66 200201
Google Scholar
[6] Ferraro M, D'annessa I, Moroni E, Morra G, Paladino A, Rinaldi S, Compostella, F, Colombo G 2019 J. Med. Chem. 62 60
Google Scholar
[7] 谢献忠, 沈伟成, 彭剑, 龙昊 2016 防灾减灾工程学报 36 972
XieX Z, Sheng W C, Peng J, Long H 2016 Journal of Disaster Prevention and Mitigation Engineering 36 972
[8] Tuttle T D, Seering W P 1996 IEEE Trans. Rob. Autom. 12 368
Google Scholar
[9] 梁晓冰, 刘希顺, 刘安芝, 王博亮 2009 58 5065
Google Scholar
Liang X B, Liu X S, Liu A Z, Wang B L 2009 Acta Phys. Sin. 58 5065
Google Scholar
[10] Li Y X, Rinzel J 1994 J. Theor. Biol. 166 461
Google Scholar
[11] Newby J M, Bressloff P C, Keener J P 2013 Phys. Rev. Lett. 111 128101
Google Scholar
[12] Zhang J J, Chen D Y, Zhang H, Xu B B, Li H H, Aggidis G A, Chatterton S 2019 J. Vib. Control 25 2863
Google Scholar
[13] He J H, Ji F Y 2019 Therm. Sci. 23 2131
Google Scholar
[14] Deng B 2004 Chaos 14 1083
Google Scholar
[15] Roberts A 2016 SIAM J. Appl.Dyn. Syst. 15 609
Google Scholar
[16] Krupa M, Touboul J D 2016 J. Dyn. Differ. Equ. 28 471
Google Scholar
[17] Golmakani A, Homburg A J 2011 Dynam Syst. 26 61
Google Scholar
[18] Cheng W, Xiang Z 2019 J. Differ. Equ. 267 3397
Google Scholar
[19] Nikolay D D, Stepan A T 2019 Appl. Math. Lett. 96 208
Google Scholar
[20] LI JZ, Tomsovic S 2019 Phys. Rev. E 99 032212
Google Scholar
[21] Han X J, Xia F B, Ji P, Bi Q S, Kurths J 2016 Commun. Nonlinear Sci. Numer. Simul. 36 517
Google Scholar
[22] Cao J D, Guerrini L, Cheng Z S 2019 Appl. Math. Comput. 343 21
[23] Li L, Wang Z, Li Y X, Shen H, Lu J W 2018 Appl. Math. Comput. 330 152
[24] Han M A, Zhang W N 2010 J. Differ. Equ. 248 2399
Google Scholar
[25] Jiang H P, Zhang T H, Song Y L 2015 Int. J. Bifurcation Chaos 25 1550058
Google Scholar
[26] Monica C, PItchaimani M 2016 Nonlinear Anal. Real World Appl. 27 55
Google Scholar
[27] Wang Z, Wang X H, Li Y X, Huang X 2017 Int. J. Bifurcation Chaos 27 1750209
Google Scholar
[28] 魏梦可, 韩修静, 张晓芳, 毕勤胜 2019 力学学报 51 904
Google Scholar
Wei M k, Han X J, Zhang X F, Bi Q S 2019 Chinese Journal of Theoretical and Applied Mechanics 51 904
Google Scholar
[29] Han X J, Bi Q S, Kurths J 2018 Phys. Rev. E 98 010201
Google Scholar
[30] Mohamad M A, Sapsis T P 2016 Ocean Eng. 120 289
Google Scholar
[31] Lakrad F, Azouani A, Abouhazim N, Belhaq M 2005 Chaos, Solitons Fractals 24 813
Google Scholar
[32] Wiggers V, Rech P C 2018 Eur. Phys. J. B 91 144
Google Scholar
[33] Shukla A K, Ramamohan T R, Srinivas S 2014 Phys. Scr. 89 075202
Google Scholar
[34] Kumar P, Kumar A, Erlicher S 2017 Physica D 358 1
Google Scholar
[35] Tamba V K, Kingni S T, Kuiate G F, Fotsin H B, Talla P K 2018 Pramana-J Phys. 91 12
Google Scholar
[36] He J H 2005 Chaos, Solitons Fractals 26 695
Google Scholar
[37] He J H 1999 Int. J. NonLinear Mech. 34 699
Google Scholar
[38] He J H, Abdou M A 2007 Chaos, Solitons Fractals 34 1421
Google Scholar
[39] He J H 2019 Results in Physics 15 102546
Google Scholar
[40] Li Y J, Wu Z Q, Wang F, Zhang G Q, Wang Y C 2019 J. Low Freq. Noise Vib. Act. Control UNSP 1461348419878534
[41] He J H 2014 Indian J. Phys. 88 193
Google Scholar
[42] Han X J, Bi Q.S, Ji P, Kurths J 2015 Phys. Rev. E 92 012911
Google Scholar
[43] Sprott J C, Li C B 2014 Phys. Rev. E 89 066901
Google Scholar
[44] Arumugam R, Sarkar S, Banerjee T, Sinha S, Dutta P S 2019 Phys. Rev. E 99 012911
DownLoad:
Catalog
Metrics
- Abstract views: 6737
- PDF Downloads: 105
- Cited By: 0
