-
Quasi-optical confocal cylindrical waveguide possesses a lot of good characteristics, such as big power capacity and low mode density, which can suppress the mode competition in beam-wave interaction. So quasi-optical waveguide has a great advantage in designing high harmonic terahertz gyrotrons. For the reason that part of electron beams located in a region of weak field intensity play a limited role in beam-wave interactions, the beam-wave interaction is not efficient in confocal cavity. Motivated by enhancing the beam-wave interaction efficiency of quasi-optical gyrotron, we propose a novel terahertz harmonic gyrotron cavity with double confocal waveguide in this paper. The transverse field distribution and the mode spectrum in double confocal waveguide are analyzed and presented. A 330 GHz second harmonic gyrotron with double confocal cavity is designed, theoretically analyzed and simulated by using a particle-in-cell (PIC) code. The results obtained for double confocal cavity are compared with the results for single confocal cavity, and the physical mechanism of beam-wave interaction enhancement in double confocal cavity is discussed. Theoretical results show that the double confocal cavity is able to increase the coupling strength of beam-wave interaction, thus, to improve the output power and the interaction efficiency of quasi-optical gyrotron. The PIC simulation results suggest that a high-order waveguide mode in double confocal cavity can steadily interact with the high harmonic cyclotron mode of electron beam without mode competition. Driven by a 40 kV, 2 A electron beam with a guiding center radius of 1.65 mm and velocity ratio equal to 1.5, output power of 9.9 kW at 328.93 GHz can be generated in the designed double confocal cavity. The beam-wave interaction efficiency increases from 5.3% in single confocal cavity to 12.4% in dual confocal cavity under the same operation parameters. The double confocal cavity has great potential applications in terahertz band. Moreover, this study indicates that the eigen mode in double confocal waveguide is a kind of hybrid mode superimposed by two independent single confocal waveguide modes. This mode characteristic will be beneficial to designing a multifrequency gyrotron oscillator operated in two modes and two cyclotron harmonics, simultaneously, with a single electron beam used, which provides a new possibility to develop the novel terahertz radiation source.
-
Keywords:
- terahertz gyrotron /
- high harmonic /
- quasi-optical cavity /
- double confocal waveguide
[1] Chu K R 2004 Rev. Mod. Phys. 76 489
Google Scholar
[2] [3] Thumm M, Denisov G G, Sakamoto K, Tran M Q 2019 Nucl. Fusion 59 073001
Google Scholar
[4] Nusinovich G S, Thumm M, Petelin M I 2014 J. Infrared Millimeter Terahertz Waves 35 325
Google Scholar
[5] Kariya T, Minami R, Okada M, et al. 2019 Nucl. Fusion 59 066009
Google Scholar
[6] Fu W J, Guan X T, Chen C, Li X Y, Yuan X S, Yan Y 2014 IEEE Trans. Electron Dev. 61 2531
Google Scholar
[7] Idehara T, Sabchevski S P 2017 J. Infrared Millimeter Terahertz Waves 38 62
Google Scholar
[8] Tsvetkov A I, Fokin A P, Sedov A S 2019 J. Infrared Millimeter Terahertz Waves 40 696
Google Scholar
[9] Kumar N, Singh U, Bera A, Sinha A K 2016 Infrared Phys. Technol. 76 38
Google Scholar
[10] 袁学松, 鄢扬, 傅文杰, 刘頔威 2012 红外与毫米波学报 31 342
Google Scholar
Yuan X S, Yan Y, Fu W J, Liu D W 2012 J. Infrared Millim. Waves 31 342
Google Scholar
[11] 黄丽萍, 洪斌斌, 刘畅, 唐昌建 2014 63 118401
Google Scholar
Huang L P, Hong B B, Liu C, Tang C J 2014 Acta Phys. Sin. 63 118401
Google Scholar
[12] Sirigiri J R, Shapiro M A, Temkin R J 2003 Phys. Rev. Lett. 90 258302
Google Scholar
[13] Ginzburg N S, Zotova I V, Sergeev A S, Zaslavsky V Y, Zheleznov I V 2012 Phys. Rev. Lett. 108 105101
Google Scholar
[14] Nanni E A, Lewis S M, Shapiro M A, Griffin R G, Temkin R J 2013 Phys. Rev. Lett. 111 235101
Google Scholar
[15] Hu W, Shapiro M, Kriescher K E, Temkin R J 1998 IEEE Trans. Plasma Sci. 26 366
Google Scholar
[16] Joye C D, Shapiro M, Sirigiri J R, Temkin R J 2009 IEEE Trans. Electron Dev. 56 818
Google Scholar
[17] Guan X T, Fu W J, Yan Y 2017 J. Infrared Millimeter Terahertz Waves 38 1457
Google Scholar
[18] Yao Y L, Wang J X, Li H, Tian Q Z, Dong K, Fu H, Lou Y 2017 IEEE Trans. Electron Dev. 64 1781
Google Scholar
[19] Soane A V, Shapiro M A, Jawla S, Temkin R J 2017 IEEE Trans. Plasma Sci. 45 2835
Google Scholar
[20] Fu W J, Guan X T, Yan Y 2019 Phys. Plasmas 26 043109
Google Scholar
[21] Yao Y L, Wang J X, Liu G, Li H, Dong K, Zhang B, Luo Y 2018 IEEE Electron Device Lett. 39 436
Google Scholar
[22] Fu W J, Guan X T, Yan Y 2016 Phys. Plasmas 23 013301
Google Scholar
[23] Guan X T, Fu W J, Lu D, Yang T B, Yan Y 2018 IEEE International Vacuum Electronics Conference (IVEC) Monterey, USA, April 24−26, 2018, pp1,2
[24] Nusinovich G S 2018 Phys. Plasmas 25 073104
Google Scholar
[25] 关晓通 2018 博士学位论文 (成都: 电子科技大学)
Guan X T 2018 Ph. D. Dissertation (Chengdu: University of Electronic Science and Technology of China) (in Chinese)
[26] Liu S G, Zhang Y X, Yin Y 2011 J. Phys. D Appl. Phys. 44 375105
Google Scholar
[27] Luchinin A G, Nusinovich G S 1984 Int. J. Electron. 57 827
Google Scholar
[28] Nusinovich G S 2019 Phys. Plasmas 26 053107
Google Scholar
[29] 韩煜, 袁学松, 马春燕, 鄢扬 2012 61 064102
Google Scholar
Han Y, Yuan X S, Ma C Y, Yan Y 2012 Acta Phys. Sin. 61 064102
Google Scholar
[30] Zhou J, Liu D G, Liao C, Li Z H 2009 IEEE Trans. Plasma Sci. 37 2002
Google Scholar
-
图 1 椭圆坐标系中的准光波导 (a)普通共焦波导; (b)双共焦波导
Figure 1. Cross section of quasi-optical waveguides in elliptic coordinate system: (a) Normal confocal waveguide; (b) double confocal waveguide.
图 2 两种波导中TE0, 11模的横向电场及环形电子注分布图 (a)普通共焦波导; (b)双共焦波导
Figure 2. Transverse geometry with the annular electron beam and electric field distributions of TE0, 11 mode in two types of quasi-optical waveguides: (a) Normal confocal waveguide; (b) double confocal waveguide.
图 3 双共焦波导模式特征值分布
Figure 3. Mode spectrum in double confocal waveguide.
图 4 双共焦谐振腔 (a)结构示意图; (b) TE0,11,1模冷腔纵向场分布图
Figure 4. Double confocal cavity: (a) Structural diagram; (b) axial field profile of TE0,11,1 mode.
图 5 双共焦波导中各模式对应注波耦合系数
$ \big\langle {{{| {{L_{\rm{s}}}} |}^2}} \big\rangle $ 随电子注引导中心半径Rb的变化Figure 5. Beam-wave coupling factors
$ \big\langle {{{| {{L_{\rm{s}}}} |}^2}} \big\rangle $ as functions of electron beam radius Rb for different modes in double confocal waveguides.
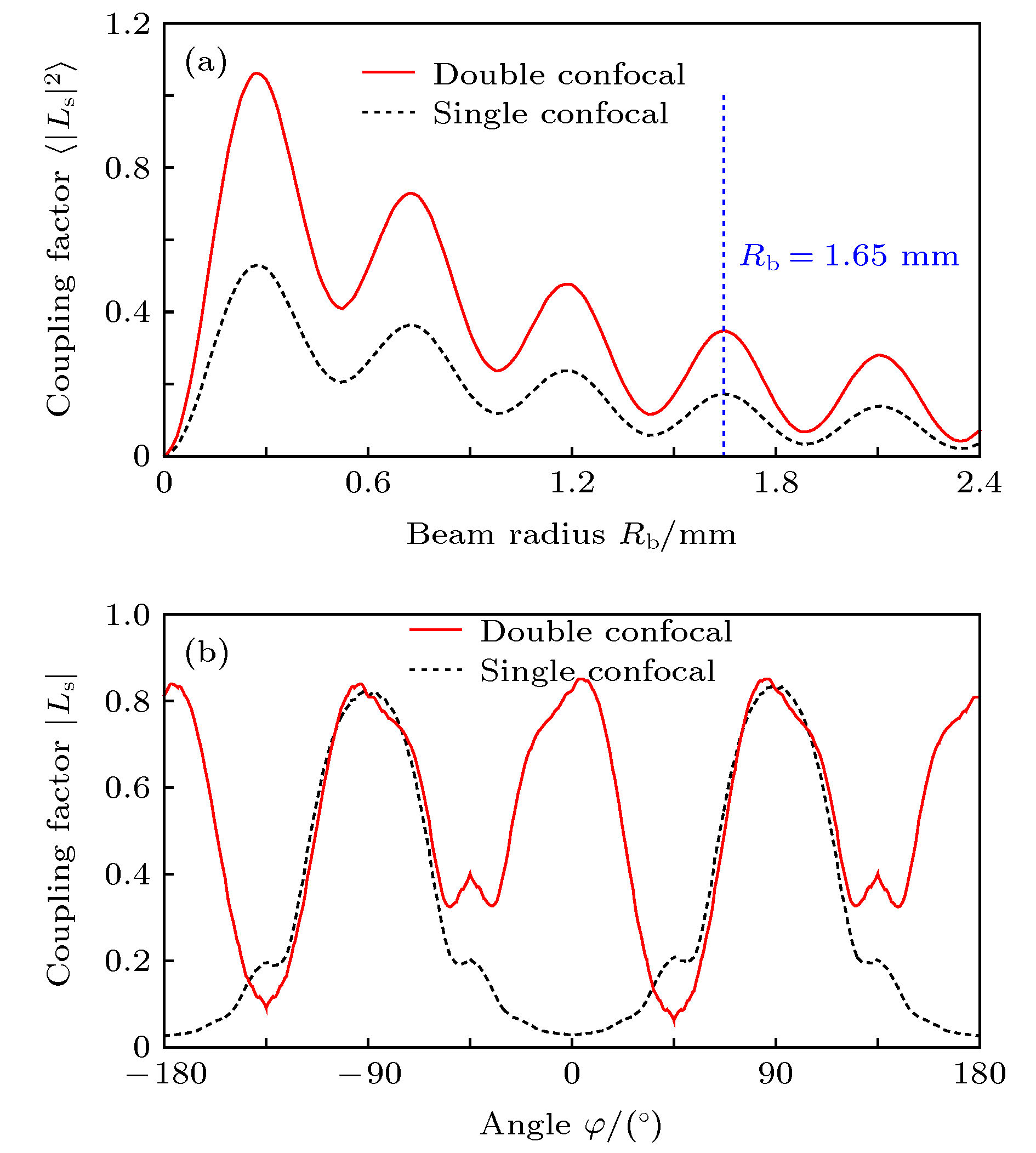
图 6 普通共焦波导和双共焦波导中TE0,11模注波耦合系数计算结果 (a) 耦合系数
$ \big\langle {{{| {{L_{\rm{s}}}} |}^2}} \big\rangle $ 沿径向的变化; (b) Rb = 1.65 mm时耦合系数|Ls|沿角向的变化Figure 6. Beam-wave coupling factors for TE0,11 mode in single and double confocal waveguide: (a) Radial distribution of coupling factor
$ \big\langle {{{| {{L_{\rm{s}}}} |}^2}} \big\rangle $ ; (b) azimuthal distribution of coupling factor Ls for an annular electron beam with Rb = 1.65 mm.
图 7 起振电流Ist的计算结果(V0 = 40 kV, α = 1.5, Rb = 1.65 mm) (a) 双共焦腔中各模式对应的Ist; (b)
${\rm{TE}}_{0, 11}^2$ 模式在双共焦腔和普通共焦腔中的IstFigure 7. Calculated results of starting current Ist (V0 = 40 kV, α = 1.5, Rb = 1.65 mm): (a) For different modes in double confocal cavity; (b) for
${\rm{TE}}_{0, 11}^2$ mode in double and single confocal cavity.
图 8 双共焦腔输出端口电场分量Ex和Ey的仿真结果 (a) 时间变化图; (b) 频谱图
Figure 8. Simulation results of output field Ex and Ey for double confocal cavity: (a) Time variation; (b) spectrum.
图 9 双共焦腔Ex分量的场分布仿真结果 (a) 输出端口; (b) xz (y = 0)平面; (c) yz (x = 0)平面
Figure 9. Simulation results of the distribution of electronic field Ex in double confocal cavity: (a) At output port; (b) at the xz plane (y = 0); (c) at the yz plane (x = 0).
图 10 双共焦腔Ey分量的场分布仿真结果 (a) 输出端口; (b) xz (y = 0)平面; (c) yz (x = 0)平面
Figure 10. Simulation results of the distribution of electronic field Ey in double confocal cavity: (a) At output port; (b) at the xz plane (y = 0); (c) at the yz plane (x = 0).
图 11 普通共焦腔仿真结果 (a) 输出端口电场Ex和Ey的时间变化图; (b) Ex的输出频谱图
Figure 11. Simulation results for single confocal cavity: (a) Time variation of the output field Ex and Ey; (b) spectrum of the output field Ex.
图 12 双共焦腔和普通共焦腔输出功率随磁场的变化
Figure 12. Simulation results of output power for double confocal cavity and single confocal cavity.
图 13 输出稳定时(100 ns)双共焦腔输出端口电场Ex和Ey随时间的变化展开图
Figure 13. Expanded results of the output field Ex and Ey for double confocal cavity around 100 ns.
表 1 双共焦波导谐振腔的设计参数
Table 1. Design parameters of the proposed double confocal cavity.
截止端镜面半径Rc1/mm 直段镜面半径Rc2 /mm 输出端镜面半径Rc3 /mm 截止段长度L1 /mm 直段长度L2 /mm 输出段长度L3 /mm 镜面宽度2a /mm 4.48 5.10 5.60 9 17 10 3.6 
DownLoad: CSV
-
[1] Chu K R 2004 Rev. Mod. Phys. 76 489
Google Scholar
[2] [3] Thumm M, Denisov G G, Sakamoto K, Tran M Q 2019 Nucl. Fusion 59 073001
Google Scholar
[4] Nusinovich G S, Thumm M, Petelin M I 2014 J. Infrared Millimeter Terahertz Waves 35 325
Google Scholar
[5] Kariya T, Minami R, Okada M, et al. 2019 Nucl. Fusion 59 066009
Google Scholar
[6] Fu W J, Guan X T, Chen C, Li X Y, Yuan X S, Yan Y 2014 IEEE Trans. Electron Dev. 61 2531
Google Scholar
[7] Idehara T, Sabchevski S P 2017 J. Infrared Millimeter Terahertz Waves 38 62
Google Scholar
[8] Tsvetkov A I, Fokin A P, Sedov A S 2019 J. Infrared Millimeter Terahertz Waves 40 696
Google Scholar
[9] Kumar N, Singh U, Bera A, Sinha A K 2016 Infrared Phys. Technol. 76 38
Google Scholar
[10] 袁学松, 鄢扬, 傅文杰, 刘頔威 2012 红外与毫米波学报 31 342
Google Scholar
Yuan X S, Yan Y, Fu W J, Liu D W 2012 J. Infrared Millim. Waves 31 342
Google Scholar
[11] 黄丽萍, 洪斌斌, 刘畅, 唐昌建 2014 63 118401
Google Scholar
Huang L P, Hong B B, Liu C, Tang C J 2014 Acta Phys. Sin. 63 118401
Google Scholar
[12] Sirigiri J R, Shapiro M A, Temkin R J 2003 Phys. Rev. Lett. 90 258302
Google Scholar
[13] Ginzburg N S, Zotova I V, Sergeev A S, Zaslavsky V Y, Zheleznov I V 2012 Phys. Rev. Lett. 108 105101
Google Scholar
[14] Nanni E A, Lewis S M, Shapiro M A, Griffin R G, Temkin R J 2013 Phys. Rev. Lett. 111 235101
Google Scholar
[15] Hu W, Shapiro M, Kriescher K E, Temkin R J 1998 IEEE Trans. Plasma Sci. 26 366
Google Scholar
[16] Joye C D, Shapiro M, Sirigiri J R, Temkin R J 2009 IEEE Trans. Electron Dev. 56 818
Google Scholar
[17] Guan X T, Fu W J, Yan Y 2017 J. Infrared Millimeter Terahertz Waves 38 1457
Google Scholar
[18] Yao Y L, Wang J X, Li H, Tian Q Z, Dong K, Fu H, Lou Y 2017 IEEE Trans. Electron Dev. 64 1781
Google Scholar
[19] Soane A V, Shapiro M A, Jawla S, Temkin R J 2017 IEEE Trans. Plasma Sci. 45 2835
Google Scholar
[20] Fu W J, Guan X T, Yan Y 2019 Phys. Plasmas 26 043109
Google Scholar
[21] Yao Y L, Wang J X, Liu G, Li H, Dong K, Zhang B, Luo Y 2018 IEEE Electron Device Lett. 39 436
Google Scholar
[22] Fu W J, Guan X T, Yan Y 2016 Phys. Plasmas 23 013301
Google Scholar
[23] Guan X T, Fu W J, Lu D, Yang T B, Yan Y 2018 IEEE International Vacuum Electronics Conference (IVEC) Monterey, USA, April 24−26, 2018, pp1,2
[24] Nusinovich G S 2018 Phys. Plasmas 25 073104
Google Scholar
[25] 关晓通 2018 博士学位论文 (成都: 电子科技大学)
Guan X T 2018 Ph. D. Dissertation (Chengdu: University of Electronic Science and Technology of China) (in Chinese)
[26] Liu S G, Zhang Y X, Yin Y 2011 J. Phys. D Appl. Phys. 44 375105
Google Scholar
[27] Luchinin A G, Nusinovich G S 1984 Int. J. Electron. 57 827
Google Scholar
[28] Nusinovich G S 2019 Phys. Plasmas 26 053107
Google Scholar
[29] 韩煜, 袁学松, 马春燕, 鄢扬 2012 61 064102
Google Scholar
Han Y, Yuan X S, Ma C Y, Yan Y 2012 Acta Phys. Sin. 61 064102
Google Scholar
[30] Zhou J, Liu D G, Liao C, Li Z H 2009 IEEE Trans. Plasma Sci. 37 2002
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7680
- PDF Downloads: 81
- Cited By: 0
