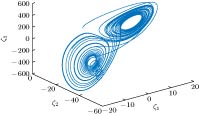
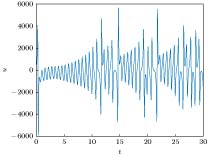
-
The problem of how to generate the Lorenz attractor from several nonlinear control systems is investigated in this paper. To be more precise, the conversions from the controlled Shimizu-Morioka system and the controlled Finance system to the Lorenz system are achieved by using the differential geometric control theory. For each case a scalar control input and a state transformation are proposed. The main approach of this paper is to convert all of those three-order systems into so called lower triangular forms which all have the same first two equations. Thus converting the controlled Shimizu-Morioka system or the controlled Finance system into the Lorenz attractor is feasible by choosing an appropriate scalar control input in the third equation of each of the two control systems. To this end, firstly, in order to use the tools of the differential geometry we construct a controlled Lorenz system by treating the vector field of the Lorenz attractor as the drift vector field and treating a linear vector field with three parameters as an input vector field. When those parameters are selected in a special manner, the conditions under which the controlled Lorenz system can be equivalently transformed into the lower triangular form are satisfied. Secondly, a state transformation, through which the controlled Lorenz system can be described as a lower triangular form, is obtained by a method like Gaussian elimination instead of solving three complicated partial differential equations. Employing several partial state transformations, choosing those three parameters and setting a scalar control input, we can reduce the equations of the controlled Lorenz system into its simplest lower triangular form. Thirdly, through two state transformations designed for the controlled Shimizu-Morioka system and the controlled Finance system respectively, the two control systems are converted into their lower triangular forms which are both similar to that of the Lorenz system in a way aforementioned. A smooth scalar controller is given to achieve the anti-control from the controlled Shimizu-Morioka system to the Lorenz attractor while another non-smooth scalar controller is designed to realize the generalized synchronization from the controlled Finance system to the Lorenz system no matter what the initial values of the two systems are. Finally, two numerical simulations demonstrate the control schemes designed in this paper.
-
Keywords:
- chaos /
- Lorenz attractor /
- state transformation /
- feedback
[1] Boccaletti S, Grebogi C, Lai Y, Mancini H L, Maza D 2000 Phys. Rep. 329 103
Google Scholar
[2] Alves P R, Duarte L G, Mota L A 2018 Chaos, Solitons Fractals 110 232
Google Scholar
[3] Moskalenko O I, Koronovskii A A, Hramov A E 2010 Phys. Lett. A 374 2925
Google Scholar
[4] Pang M, Huang Y 2018 Chin. Phys. B 27 118902
Google Scholar
[5] Wang J, Duan L, Kang Q 2017 Chin. Phys. Lett. 34 074703
Google Scholar
[6] Moreno-Valenzuela J 2013 Commun. Nonlinear Sci. 18 1
Google Scholar
[7] Yan S 2016 Chin. Phys. B 25 90504
Google Scholar
[8] 王芳, 张新政, 申朝文, 禹思敏 2012 61 190505
Google Scholar
Wang F, Zhang X Z, Shen C W, Yu S M 2012 Acta Phys. Sin. 61 190505
Google Scholar
[9] Pecora L M, Carroll T L 2015 Chaos 25 097611
Google Scholar
[10] Rulkov N F, Sushchik M M, Tsimring L S, Abarbanel H D 1995 Phys. Rev. E 51 980
Google Scholar
[11] Abarbanel H D I, Rulkov N F, Sushchik M M 1996 Phys. Rev. E 53 4528
[12] Parlitz U, Junge L, Kocarev L 1997 Phys. Rev. Lett. 79 3158
Google Scholar
[13] Zang H Y, Min L Q, Zhao G, Chen G R 2013 Chin. Phys. Lett. 30 040502
Google Scholar
[14] Wu X, Guan Z, Wu Z, Li T 2007 Phys. Lett. A 364 484
Google Scholar
[15] Ojo K S, Ogunjo S T, Njah A N, Fuwape I 2015 Pramana-J. Phys. 84 33
Google Scholar
[16] Zhang G, Liu Z, Ma Z 2007 Chaos, Solitons Fractals 32 773
Google Scholar
[17] Wang X F, Chen G 2003 IEEE Trans. Circ. Syst. I 50 812
Google Scholar
[18] Zhang J, Li C, Zhang H, Yu J 2004 Chaos, Solitons Fractals 21 1183
Google Scholar
[19] Wang F, Chen S, Yu M, Wang C 2004 Chaos, Solitons Fractals 22 927
Google Scholar
[20] Hramov A E, Koronovskii A A 2005 Phys. Rev. E 71 067201
Google Scholar
[21] Hu A, Xu Z, Guo L 2009 Phys. Lett. A 373 2319
Google Scholar
[22] Zhou J, Chen J, Lu J, Lü J 2017 IEEE Trans. Automat. Contr. 62 3468
Google Scholar
[23] Shimizu T, Morioka N 1980 Phys. Lett. A 76 201
Google Scholar
[24] Ma C, Wang X 2012 Commun. Nonlinear Sci. 17 721
Google Scholar
[25] Lorenz E N 1963 J. Atmos. Sci. 20 130
Google Scholar
[26] Celikovsky S, Nijmeijer H 1996 Syst. Control Lett. 27 135
Google Scholar
[27] Khalil H K 2002 Nonlinear Systems (Londan: Prentice Hall) pp521−530
[28] Fecko M 2006 Differential Geometry and Lie Groups for Physicists (Cambridge: Cambridge University Press) pp21−91, 524−550
[29] Haimo V T 1986 SIAM J. Control Optim. 24 760
Google Scholar
-
图 1 Lorenz系统轨迹
Figure 1. Trajectory of the Lorenz system.
图 2 受控Shimizu-Morioka系统轨迹
Figure 2. Trajectory of the controlled Shimizu-Morioka system
图 3 受控Shimizu-Morioka系统的标量控制输入
Figure 3. Scale control input for the controlled Shimizu-Morioka system.
图 4 经状态变换
${{{T}}^{ - 1}}({{\tau }}({{\zeta }}))$ 受控Shimizu-Morioka系统轨迹Figure 4. Trajectory of the controlled Shimizu-Morioka system via the state transformation
${{{T}}^{ - 1}}({{\tau }}({{\zeta }}))$ .
图 5 受控Finance系统轨迹
Figure 5. Trajectory of the controlled Finance system.
图 6 受控Finance系统的标量控制输入
Figure 6. Scale control input for the controlled Finance system
图 7 经状态变换
${{{T}}^{ - 1}}({{\tau }}({{\zeta }}))$ 受控Finance系统轨迹Figure 7. Trajectory of the controlled Shimizu-Morioka system via the state transformation
${{{T}}^{ - 1}}({{\tau }}({{\zeta }}))$ .
图 8 Lorenz系统轨迹与经状态变换
${{{T}}^{ - 1}}({{\tau }}({{\zeta }}))$ 的受控Finance系统的误差Figure 8. Error between the trajectory of the Lorenz system and that of the controlled Finance system via the state transformation
${{{T}}^{ - 1}}({{\tau }}({{\zeta }}))$ . -
[1] Boccaletti S, Grebogi C, Lai Y, Mancini H L, Maza D 2000 Phys. Rep. 329 103
Google Scholar
[2] Alves P R, Duarte L G, Mota L A 2018 Chaos, Solitons Fractals 110 232
Google Scholar
[3] Moskalenko O I, Koronovskii A A, Hramov A E 2010 Phys. Lett. A 374 2925
Google Scholar
[4] Pang M, Huang Y 2018 Chin. Phys. B 27 118902
Google Scholar
[5] Wang J, Duan L, Kang Q 2017 Chin. Phys. Lett. 34 074703
Google Scholar
[6] Moreno-Valenzuela J 2013 Commun. Nonlinear Sci. 18 1
Google Scholar
[7] Yan S 2016 Chin. Phys. B 25 90504
Google Scholar
[8] 王芳, 张新政, 申朝文, 禹思敏 2012 61 190505
Google Scholar
Wang F, Zhang X Z, Shen C W, Yu S M 2012 Acta Phys. Sin. 61 190505
Google Scholar
[9] Pecora L M, Carroll T L 2015 Chaos 25 097611
Google Scholar
[10] Rulkov N F, Sushchik M M, Tsimring L S, Abarbanel H D 1995 Phys. Rev. E 51 980
Google Scholar
[11] Abarbanel H D I, Rulkov N F, Sushchik M M 1996 Phys. Rev. E 53 4528
[12] Parlitz U, Junge L, Kocarev L 1997 Phys. Rev. Lett. 79 3158
Google Scholar
[13] Zang H Y, Min L Q, Zhao G, Chen G R 2013 Chin. Phys. Lett. 30 040502
Google Scholar
[14] Wu X, Guan Z, Wu Z, Li T 2007 Phys. Lett. A 364 484
Google Scholar
[15] Ojo K S, Ogunjo S T, Njah A N, Fuwape I 2015 Pramana-J. Phys. 84 33
Google Scholar
[16] Zhang G, Liu Z, Ma Z 2007 Chaos, Solitons Fractals 32 773
Google Scholar
[17] Wang X F, Chen G 2003 IEEE Trans. Circ. Syst. I 50 812
Google Scholar
[18] Zhang J, Li C, Zhang H, Yu J 2004 Chaos, Solitons Fractals 21 1183
Google Scholar
[19] Wang F, Chen S, Yu M, Wang C 2004 Chaos, Solitons Fractals 22 927
Google Scholar
[20] Hramov A E, Koronovskii A A 2005 Phys. Rev. E 71 067201
Google Scholar
[21] Hu A, Xu Z, Guo L 2009 Phys. Lett. A 373 2319
Google Scholar
[22] Zhou J, Chen J, Lu J, Lü J 2017 IEEE Trans. Automat. Contr. 62 3468
Google Scholar
[23] Shimizu T, Morioka N 1980 Phys. Lett. A 76 201
Google Scholar
[24] Ma C, Wang X 2012 Commun. Nonlinear Sci. 17 721
Google Scholar
[25] Lorenz E N 1963 J. Atmos. Sci. 20 130
Google Scholar
[26] Celikovsky S, Nijmeijer H 1996 Syst. Control Lett. 27 135
Google Scholar
[27] Khalil H K 2002 Nonlinear Systems (Londan: Prentice Hall) pp521−530
[28] Fecko M 2006 Differential Geometry and Lie Groups for Physicists (Cambridge: Cambridge University Press) pp21−91, 524−550
[29] Haimo V T 1986 SIAM J. Control Optim. 24 760
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6143
- PDF Downloads: 64
- Cited By: 0
