压缩过程中允许临时重叠对硬质颗粒体系密排密度及构型的影响

张书琛; 万端端

doi:10.7498/aps.74.20250552

摘要

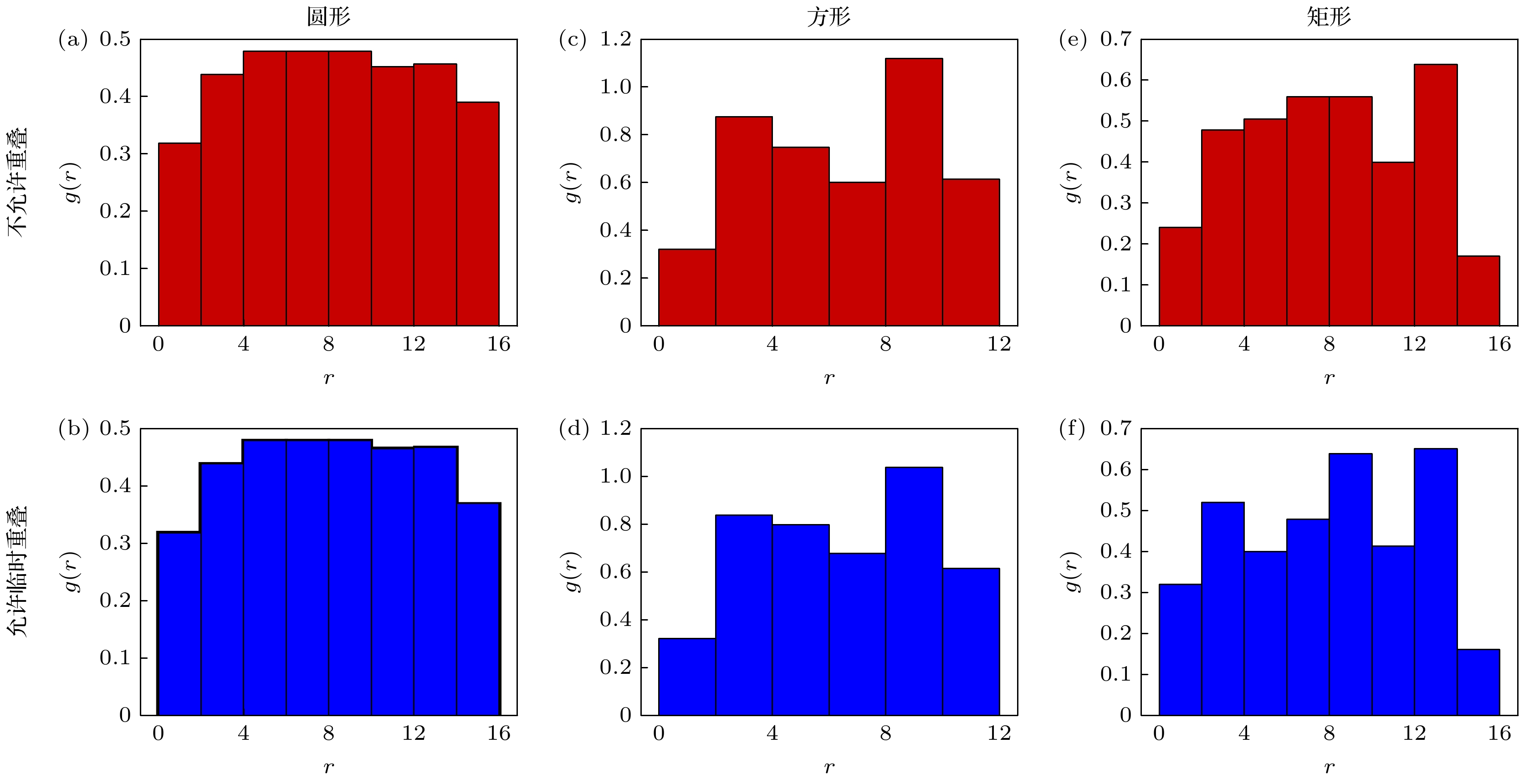
硬质颗粒在受限空间中的致密排列具有重要的物理意义, 并为许多其他物理系统提供了启发. 如何实现硬质颗粒在受限空间中的高密度排列, 是一个具有挑战性的问题. 本文运用蒙特卡罗方法, 结合边界压缩机制, 研究了二维圆形、正方形和长宽比为5∶1的矩形颗粒在圆形受限空间中的致密排列. 具体而言, 探讨了在压缩过程中不允许颗粒重叠以及允许少数颗粒重叠、后移除重叠(允许临时重叠)两种方法下所能获得的最高密度. 研究发现, 允许临时重叠的方法能够实现更高的密排构型. 本文进一步比较了两种压缩方式下获得的构型的径向分布函数和取向序参量, 发现两者具有相似的特征, 但允许临时重叠的方式在更大区域内显示出有序性. 研究结果表明, 允许颗粒临时重叠可能是提高受限空间中排列密度的有效途径.

关键词:

硬质颗粒 /
重叠 /
排列密度 /
构型

Abstract

The dense packing of hard particles in confined spaces has sparked widespread interest in mathematics and statistical physics. It relates to classical packing problems, plays a central role in understanding the self-assembly of microscopic particles such as colloids and nanoparticles under geometric constraints, and inspires studies on a wide range of physical systems. However, achieving high packing densities under confinement remains challenging due to anisotropic shapes of particles, the discontinuous nature of hard-core interactions, and geometric frustration. In this work, we develop a Monte Carlo scheme that combines boundary compression with controlled temporary particle overlaps. Specifically, during the compression of a circular boundary,we allow a limited number of overlaps which are then removed before further compression steps. We apply this strategy to three types of two-dimensional particles-disks, squares, and rectangles with an aspect ratio of 5∶1—confined within a circular boundary. As a control, we also perform simulations using a traditional method that strictly prohibits overlaps throughout. The final configurations from both methods exhibit similar structural features. For hard disks, central particles form a triangular lattice, while those near the boundary become more disordered to accommodate the circular geometry. For hard squares, particles in the center organize into a square lattice, whereas those near the boundary form concentric layers. For rectangles, particles in the central region display local smectic-like alignment within clusters that are oriented nearly perpendicular to each other. Near the boundary, some particles align tangentially along the circular edge. Quantitatively, the temporary-overlap strategy consistently yields denser packing across all particle types. The analysis shows that the average packing density and maximal packing density of 10 independent samples obtained from the above strategy are higher than those from the traditional method. Further analysis of the radial distribution functions and orientational order parameters reveals that although both methods produce similar structural features, the overlap-allowed method yields a larger central region exhibiting lattice-like or cluster-like ordering. Our findings suggest that allowing temporary particle overlaps is an effective strategy for generating dense configurations of hard particles under confinement. This approach may be extended to more complex systems, including three-dimensional particles or mixtures of particles of different shapes confined within restricted geometries.

Keywords:

作者及机构信息

武汉大学物理科学与技术学院, 武汉　430072

通信作者: 万端端, ddwan@whu.edu.cn

基金项目: 国家自然科学基金(批准号: 12274330)和武汉市知识创新专项曙光计划(批准号: 2022010801020125)资助的课题.

Authors and contacts

School of Physics and Technology, Wuhan University, Wuhan 430072, China

Corresponding author: WAN Duanduan, ddwan@whu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 12274330) and the Knowledge Innovation Special Program of Wuhan-Shuguang, China (Grant No. 2022010801020125).

文章全文

参考文献

[1]	Conway J H, Sloane N J A 2013 Sphere Packings, Lattices and Groups (Vol. 290) (New York: Springer Science & Business Media
[2]	Velev O D, Lenhoff A M, Kaler E W 2000 Science 287 2240 Google Scholar
[3]	De Nijs B, Dussi S, Smallenburg F, Meeldijk J D, Groenendijk D J, Filion L, Imhof A, Van Blaaderen A, Dijkstra M 2015 Nat. Mater. 14 56 Google Scholar
[4]	Chen Y, Yao Z, Tang S, Tong H, Yanagishima T, Tanaka H, Tan P 2021 Nat. Phys. 17 121 Google Scholar
[5]	Wang D, Dasgupta T, van der Wee E B, Zanaga D, Altantzis T, Wu Y, Coli G M, Murray C B, Bals S, Dijkstra M 2021 Nat. Phys. 17 128 Google Scholar
[6]	Wang D, Hermes M, Kotni R, Wu Y, Tasios N, Liu Y, De Nijs B, Van Der Wee E B, Murray C B, Dijkstra M 2018 Nat. Commun. 9 2228 Google Scholar
[7]	吴赛, 李伟斌, 石峰, 蒋世春, 蓝鼎, 王育人 2015 64 096101 Google Scholar Wu S, Li W B, Shi F, Jiang S C, Lan D, Wang Y R 2015 Acta Phys. Sin. 64 096101 Google Scholar
[8]	刘心卓, 王华光 2020 69 238201 Google Scholar Liu X Z, Wang H G 2020 Acta Phys. Sin. 69 238201 Google Scholar
[9]	Marino E, LaCour R A, Kodger T E 2024 Cryst. Growth Des. 24 6060 Google Scholar
[10]	Boles M A, Engel M, Talapin D V 2016 Chem. Rev. 116 11220 Google Scholar
[11]	Glotzer S C, Solomon M J 2007 Nat. Mater. 6 557 Google Scholar
[12]	Marenduzzo D, Micheletti C, Orlandini E 2010 J. Phys. Condens. Matter 22 283102 Google Scholar
[13]	Ellis R J 2001 Trends Biochem. Sci. 26 597 Google Scholar
[14]	Cines D B, Lebedeva T, Nagaswami C, Hayes V, Massefski W, Litvinov R I, Rauova L, Lowery T J, Weisel J W 2014 Blood 123 1596 Google Scholar
[15]	Hayashi T, Carthew R W 2004 Nature 431 647 Google Scholar
[16]	van Roij R, Dijkstra M, Evans R 2000 Europhys. Lett. 49 350 Google Scholar
[17]	de las Heras D, Velasco E, Mederos L 2005 Phys. Rev. Lett. 94 017801 Google Scholar
[18]	Galanis J, Nossal R, Losert W, Harries D 2010 Phys. Rev. Lett. 105 168001 Google Scholar
[19]	Chen J Z 2013 Soft Matter 9 10921 Google Scholar
[20]	Burada P S, Schmid G, Reguera D, Vainstein M H, Rubi J, Hänggi P 2008 Phys. Rev. Lett. 101 130602 Google Scholar
[21]	Reguera D, Luque A, Burada P S, Schmid G, Rubi J, Hänggi P 2012 Phys. Rev. Lett. 108 020604 Google Scholar
[22]	Oosawa F, Asakura S 1954 J. Chem. Phys. 22 1255
[23]	Asakura S, Oosawa F 1958 J. Polym. Sci. 33 183 Google Scholar
[24]	Crocker J C, Matteo J A, Dinsmore A D, Yodh A G 1999 Phys. Rev. Lett. 82 4352 Google Scholar
[25]	Zhao K, Mason T G 2007 Phys. Rev. Lett. 99 268301 Google Scholar
[26]	Zhao K, Mason T G 2008 Phys. Rev. Lett. 101 148301 Google Scholar
[27]	马红孺 2016 65 184701 Google Scholar Ma H R 2016 Acta Phys. Sin. 65 184701 Google Scholar
[28]	Mughal A, Chan H, Weaire D, Hutzler S 2012 Phys. Rev. E 85 051305 Google Scholar
[29]	Chen D, Torquato S 2015 Phys. Rev. E 92 062207 Google Scholar
[30]	Oğuz E C, Marechal M, Ramiro-Manzano F, Rodriguez I, Messina R, Meseguer F J, Löwen H 2012 Phys. Rev. Lett. 109 218301 Google Scholar
[31]	Teich E G, Van Anders G, Klotsa D, Dshemuchadse J, Glotzer S C 2016 Proc. Natl. Acad. Sci. U. S. A. 113 E669
[32]	Wan D, Glotzer S C 2018 Soft Matter 14 3012 Google Scholar
[33]	Haji-Akbari A, Engel M, Keys A S, Zheng X, Petschek R G, Palffy-Muhoray P, Glotzer S C 2009 Nature 462 773 Google Scholar
[34]	Gang O, Zhang Y 2011 ACS Nano 5 8459 Google Scholar
[35]	Kraft D J, Ni R, Smallenburg F, Hermes M, Yoon K, Weitz D A, van Blaaderen A, Groenewold J, Dijkstra M, Kegel W K 2012 Proc. Natl. Acad. Sci. U. S. A. 109 10787 Google Scholar
[36]	Agarwal U, Escobedo F A 2011 Nat. Mater. 10 230 Google Scholar
[37]	Damasceno P F, Engel M, Glotzer S C 2012 Science 337 453 Google Scholar
[38]	Ni R, Gantapara A P, De Graaf J, Van Roij R, Dijkstra M 2012 Soft Matter 8 8826 Google Scholar
[39]	Marechal M, Kortschot R J, Demirörs A F, Imhof A, Dijkstra M 2010 Nano Lett. 10 1907 Google Scholar
[40]	Chen D, Jiao Y, Torquato S 2014 J. Phys. Chem. B 118 7981 Google Scholar
[41]	Wan D, Du C X, van Anders G and Glotzer S C 2019 J. Phys. Chem. B 123 9038 Google Scholar
[42]	Anderson J A, Glaser J, Glotzer S C 2020 Comput. Mater. Sci. 173 109363 Google Scholar
[43]	Specht E http://hydra.nat.uni-magdeburg.de/packing/
[44]	Steinhardt P J, Nelson D R, Ronchetti M 1983 Phys. Rev. B 28 784 Google Scholar
[45]	Walsh L, Menon N 2016 J. Stat. Mech: Theory Exp. 2016 083302 Google Scholar
[46]	Anderson J A, Antonaglia J, Millan J A, Engel M, Glotzer S C 2017 Phys. Rev. X 7 021001 Google Scholar

施引文献

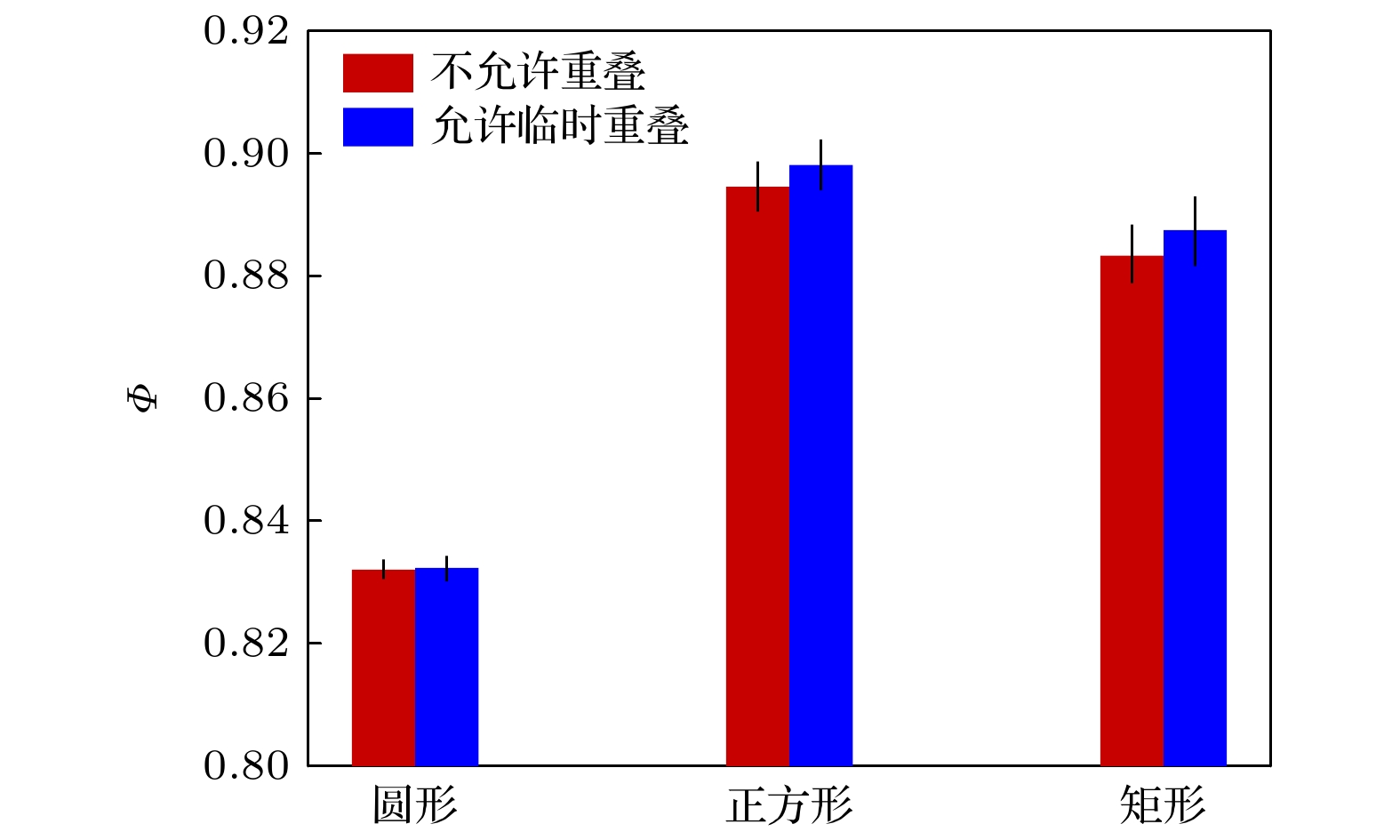
图 1 不允许重叠和允许临时重叠两种压缩方式得到的密度$ \varPhi $. 每个形状取了10个独立样本做平均, 误差线为标准差

Fig. 1. Average maximum packing densities $ \varPhi $ achieved using two methods: one disallowing overlaps and the other allowing a few temporary overlaps. Results are averaged over 10 independent samples, with error bars indicating the standard error.

下载: 全尺寸图片幻灯片

图 2 最高密度构型中, 颗粒质心的径向分布函数$g\left( r \right)$之于颗粒到圆心距离$r$

Fig. 2. Radial distribution function $g\left( r \right)$ of particle centers as a function of the distance $r$ from the center in the highest-density configuration.

下载: 全尺寸图片幻灯片

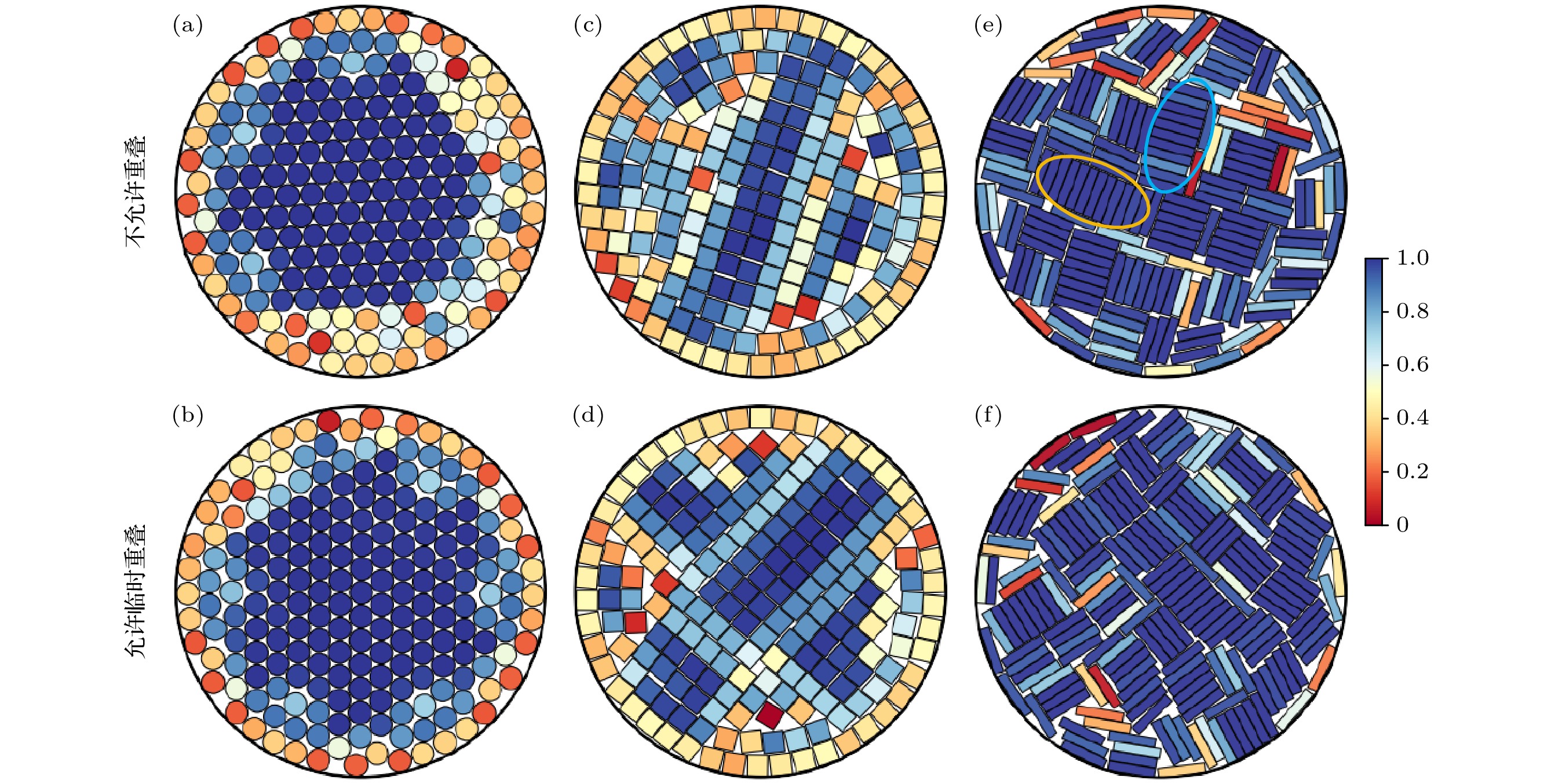
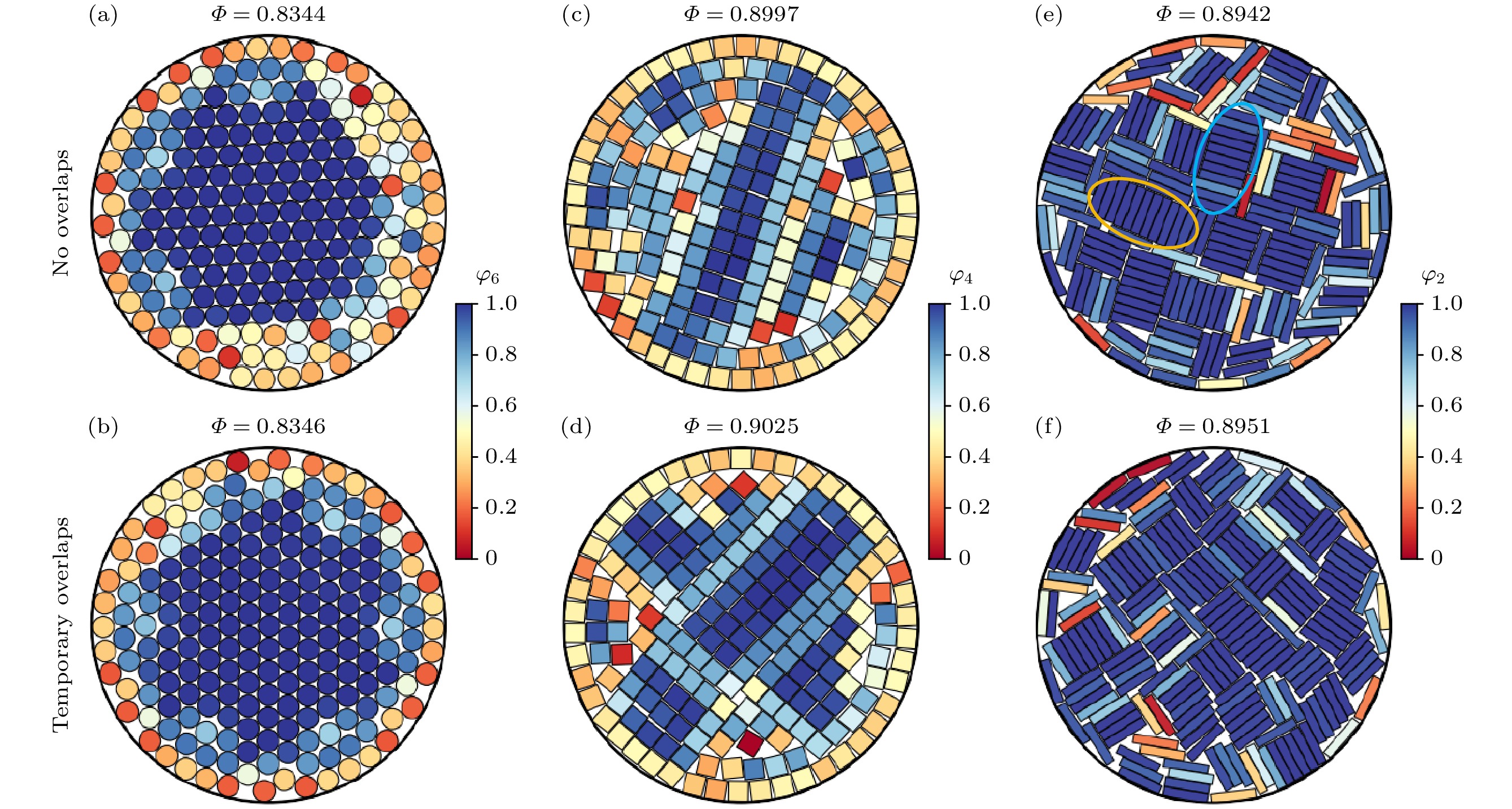
图 3 硬盘、正方形和矩形颗粒最密排列结构. 粒子颜色分别对应了序参数${\varphi _{6 j}}$, ${\varphi _{4 j}}$和${\varphi _{2 j}}$的大小. 图(e)中标出了矩形颗粒形成的局部簇(黄色和蓝色圆圈)

Fig. 3. Densest configurations from the two methods. The color bar of disks, squares and rectangles correspond to the magnitude of the order parameters ${\varphi _{6 j}}$, ${\varphi _{4 j}}$ and ${\varphi _{2 j}}$, respectively. In panel (e), local clusters of rectangular particles are marked with yellow and blue circles.

下载: 全尺寸图片幻灯片

下载: 全尺寸图片幻灯片

表 1 10个样品中粒子的最大密排密度

Table 1. Maximum packing density of particles across 10 independent samples.

粒子形状不允许重叠允许临时重叠

圆形 0.8344 0.8346
正方形 0.8997 0.9025
矩形 0.8942 0.8951

下载: 导出CSV

表 2 最密堆积构型中粒子的全局序参数

Table 2. Value of order parameter ${\varphi _n}$ in the densest packing configuration.

粒子序参量不允许重叠允许临时重叠

圆形(${\varphi _6}$) 0.6329 0.7250
正方形(${\varphi _4}$) 0.3298 0.4644
矩形(${\varphi _2}$) 0.1255 0.05013

下载: 导出CSV

map

[1]	Conway J H, Sloane N J A 2013 Sphere Packings, Lattices and Groups (Vol. 290) (New York: Springer Science & Business Media
[2]	Velev O D, Lenhoff A M, Kaler E W 2000 Science 287 2240 Google Scholar
[3]	De Nijs B, Dussi S, Smallenburg F, Meeldijk J D, Groenendijk D J, Filion L, Imhof A, Van Blaaderen A, Dijkstra M 2015 Nat. Mater. 14 56 Google Scholar
[4]	Chen Y, Yao Z, Tang S, Tong H, Yanagishima T, Tanaka H, Tan P 2021 Nat. Phys. 17 121 Google Scholar
[5]	Wang D, Dasgupta T, van der Wee E B, Zanaga D, Altantzis T, Wu Y, Coli G M, Murray C B, Bals S, Dijkstra M 2021 Nat. Phys. 17 128 Google Scholar
[6]	Wang D, Hermes M, Kotni R, Wu Y, Tasios N, Liu Y, De Nijs B, Van Der Wee E B, Murray C B, Dijkstra M 2018 Nat. Commun. 9 2228 Google Scholar
[7]	吴赛, 李伟斌, 石峰, 蒋世春, 蓝鼎, 王育人 2015 64 096101 Google Scholar Wu S, Li W B, Shi F, Jiang S C, Lan D, Wang Y R 2015 Acta Phys. Sin. 64 096101 Google Scholar
[8]	刘心卓, 王华光 2020 69 238201 Google Scholar Liu X Z, Wang H G 2020 Acta Phys. Sin. 69 238201 Google Scholar
[9]	Marino E, LaCour R A, Kodger T E 2024 Cryst. Growth Des. 24 6060 Google Scholar
[10]	Boles M A, Engel M, Talapin D V 2016 Chem. Rev. 116 11220 Google Scholar
[11]	Glotzer S C, Solomon M J 2007 Nat. Mater. 6 557 Google Scholar
[12]	Marenduzzo D, Micheletti C, Orlandini E 2010 J. Phys. Condens. Matter 22 283102 Google Scholar
[13]	Ellis R J 2001 Trends Biochem. Sci. 26 597 Google Scholar
[14]	Cines D B, Lebedeva T, Nagaswami C, Hayes V, Massefski W, Litvinov R I, Rauova L, Lowery T J, Weisel J W 2014 Blood 123 1596 Google Scholar
[15]	Hayashi T, Carthew R W 2004 Nature 431 647 Google Scholar
[16]	van Roij R, Dijkstra M, Evans R 2000 Europhys. Lett. 49 350 Google Scholar
[17]	de las Heras D, Velasco E, Mederos L 2005 Phys. Rev. Lett. 94 017801 Google Scholar
[18]	Galanis J, Nossal R, Losert W, Harries D 2010 Phys. Rev. Lett. 105 168001 Google Scholar
[19]	Chen J Z 2013 Soft Matter 9 10921 Google Scholar
[20]	Burada P S, Schmid G, Reguera D, Vainstein M H, Rubi J, Hänggi P 2008 Phys. Rev. Lett. 101 130602 Google Scholar
[21]	Reguera D, Luque A, Burada P S, Schmid G, Rubi J, Hänggi P 2012 Phys. Rev. Lett. 108 020604 Google Scholar
[22]	Oosawa F, Asakura S 1954 J. Chem. Phys. 22 1255
[23]	Asakura S, Oosawa F 1958 J. Polym. Sci. 33 183 Google Scholar
[24]	Crocker J C, Matteo J A, Dinsmore A D, Yodh A G 1999 Phys. Rev. Lett. 82 4352 Google Scholar
[25]	Zhao K, Mason T G 2007 Phys. Rev. Lett. 99 268301 Google Scholar
[26]	Zhao K, Mason T G 2008 Phys. Rev. Lett. 101 148301 Google Scholar
[27]	马红孺 2016 65 184701 Google Scholar Ma H R 2016 Acta Phys. Sin. 65 184701 Google Scholar
[28]	Mughal A, Chan H, Weaire D, Hutzler S 2012 Phys. Rev. E 85 051305 Google Scholar
[29]	Chen D, Torquato S 2015 Phys. Rev. E 92 062207 Google Scholar
[30]	Oğuz E C, Marechal M, Ramiro-Manzano F, Rodriguez I, Messina R, Meseguer F J, Löwen H 2012 Phys. Rev. Lett. 109 218301 Google Scholar
[31]	Teich E G, Van Anders G, Klotsa D, Dshemuchadse J, Glotzer S C 2016 Proc. Natl. Acad. Sci. U. S. A. 113 E669
[32]	Wan D, Glotzer S C 2018 Soft Matter 14 3012 Google Scholar
[33]	Haji-Akbari A, Engel M, Keys A S, Zheng X, Petschek R G, Palffy-Muhoray P, Glotzer S C 2009 Nature 462 773 Google Scholar
[34]	Gang O, Zhang Y 2011 ACS Nano 5 8459 Google Scholar
[35]	Kraft D J, Ni R, Smallenburg F, Hermes M, Yoon K, Weitz D A, van Blaaderen A, Groenewold J, Dijkstra M, Kegel W K 2012 Proc. Natl. Acad. Sci. U. S. A. 109 10787 Google Scholar
[36]	Agarwal U, Escobedo F A 2011 Nat. Mater. 10 230 Google Scholar
[37]	Damasceno P F, Engel M, Glotzer S C 2012 Science 337 453 Google Scholar
[38]	Ni R, Gantapara A P, De Graaf J, Van Roij R, Dijkstra M 2012 Soft Matter 8 8826 Google Scholar
[39]	Marechal M, Kortschot R J, Demirörs A F, Imhof A, Dijkstra M 2010 Nano Lett. 10 1907 Google Scholar
[40]	Chen D, Jiao Y, Torquato S 2014 J. Phys. Chem. B 118 7981 Google Scholar
[41]	Wan D, Du C X, van Anders G and Glotzer S C 2019 J. Phys. Chem. B 123 9038 Google Scholar
[42]	Anderson J A, Glaser J, Glotzer S C 2020 Comput. Mater. Sci. 173 109363 Google Scholar
[43]	Specht E http://hydra.nat.uni-magdeburg.de/packing/
[44]	Steinhardt P J, Nelson D R, Ronchetti M 1983 Phys. Rev. B 28 784 Google Scholar
[45]	Walsh L, Menon N 2016 J. Stat. Mech: Theory Exp. 2016 083302 Google Scholar
[46]	Anderson J A, Antonaglia J, Millan J A, Engel M, Glotzer S C 2017 Phys. Rev. X 7 021001 Google Scholar

[1]	王博维, 商姊萌, 韩伟华. 量子点阵列几何构型对电子跃迁输运的调控. , 2025, 74(19): . doi: 10.7498/aps.74.20250784
[2]	赵永鹏, 豆艳坤, 贺新福, 杨文. Ti-V-Ta多主元合金辐照位错环形成的级联重叠模拟. , 2024, 73(22): 226102. doi: 10.7498/aps.73.20241074
[3]	王前进, 孙鹏帅, 张志荣, 张乐文, 杨曦, 吴边, 庞涛, 夏滑, 李启勇. 混合气体测量中重叠吸收谱线交叉干扰的分离解析方法. , 2021, 70(14): 144203. doi: 10.7498/aps.70.20210286
[4]	江鹏, 毕卫红, 齐跃峰, 付兴虎, 武洋, 田朋飞. 光子晶体光纤重叠光栅理论模型与光谱特性研究. , 2016, 65(20): 204208. doi: 10.7498/aps.65.204208
[5]	左小伟, 安佰灵, 黄德洋, 张林, 王恩刚. 强磁场作用下Cu熔体中富Fe颗粒的迁移与排列. , 2016, 65(13): 137401. doi: 10.7498/aps.65.137401
[6]	杨光敏, 徐强, 李冰, 张汉壮, 贺小光. 不同N掺杂构型石墨烯的量子电容研究. , 2015, 64(12): 127301. doi: 10.7498/aps.64.127301
[7]	李金洋, 逯丹凤, 祁志美. 铌酸锂波导电光重叠积分因子的波长依赖特性分析. , 2014, 63(7): 077801. doi: 10.7498/aps.63.077801
[8]	徐国亮, 张琳, 路战胜, 刘培, 刘玉芳. 特殊构型Si2N2分子团簇电致激发特性的密度泛函理论研究. , 2014, 63(10): 103101. doi: 10.7498/aps.63.103101
[9]	狄慧鸽, 华灯鑫, 王玉峰, 闫庆. 米散射激光雷达重叠因子及全程回波信号标定技术研究. , 2013, 62(9): 094215. doi: 10.7498/aps.62.094215
[10]	侯威, 章大全, 杨萍, 杨杰. 去趋势波动分析方法中不重叠等长度子区间长度的确定. , 2010, 59(12): 8986-8993. doi: 10.7498/aps.59.8986
[11]	周晶晶, 陈云贵, 吴朝玲, 肖艳, 高涛. NaAlH4 表面Ti催化空间构型和X射线吸收光谱: Car-Parrinello分子动力学和密度泛函理论研究. , 2010, 59(10): 7452-7457. doi: 10.7498/aps.59.7452
[12]	徐勇, 王贤龙, 曾雉. 中性和带电小钨团簇的第一性原理研究. , 2009, 58(13): 72-S78. doi: 10.7498/aps.58.72
[13]	田丽君, 刘天亮, 黄海军. 含重叠路段交通系统中信息反馈策略的比较研究. , 2008, 57(4): 2122-2129. doi: 10.7498/aps.57.2122
[14]	孙一翎, 潘剑侠. 多模干涉耦合器中重叠像相干相消现象分析. , 2007, 56(6): 3300-3305. doi: 10.7498/aps.56.3300
[15]	阎世英, 马美仲, 朱正和. B2H6分子的几何构型. , 2005, 54(7): 3106-3110. doi: 10.7498/aps.54.3106
[16]	马宏伟, 梁敬魁. 从x射线粉末数据获得非等效本征重叠衍射的合理衍射强度. , 2004, 53(3): 829-834. doi: 10.7498/aps.53.829
[17]	谢晓明, 蒋亦民, 王焕友, 曹晓平, 刘佑. 颗粒堆密度变化对堆底压力分布的影响. , 2003, 52(9): 2194-2199. doi: 10.7498/aps.52.2194
[18]	汪蓉, 朱正和, 杨传路. C42+的几何构型和Jahn Teller效应. , 2001, 50(9): 1675-1680. doi: 10.7498/aps.50.1675
[19]	万钧, 叶令, 王迅. Si中掺Er的原子构型与电子特性. , 1998, 47(4): 652-657. doi: 10.7498/aps.47.652
[20]	陈仁术, 西门纪业. 扇形重叠场中三级离子轨迹理论(Ⅰ)——轨迹计算和矩阵表示. , 1982, 31(6): 722-737. doi: 10.7498/aps.31.722

计量

文章访问数: 378
PDF下载量: 17
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

压缩过程中允许临时重叠对硬质颗粒体系密排密度及构型的影响