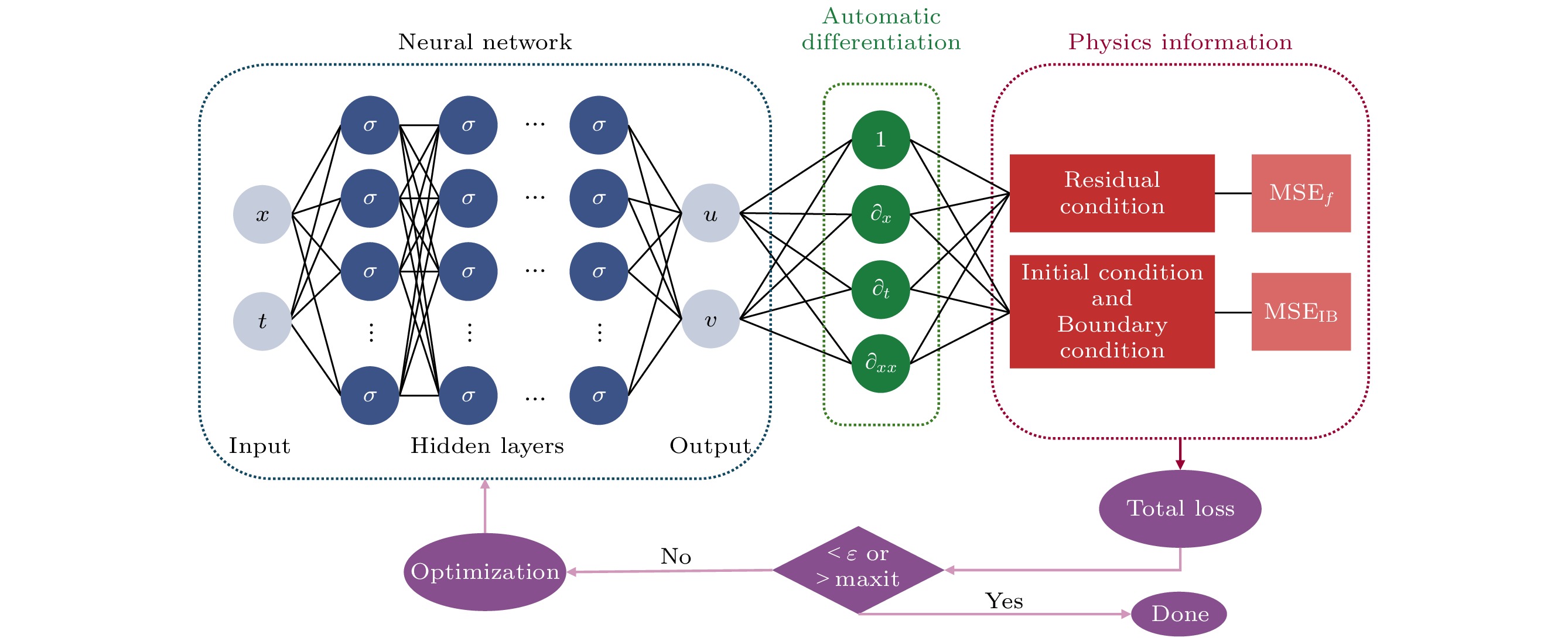
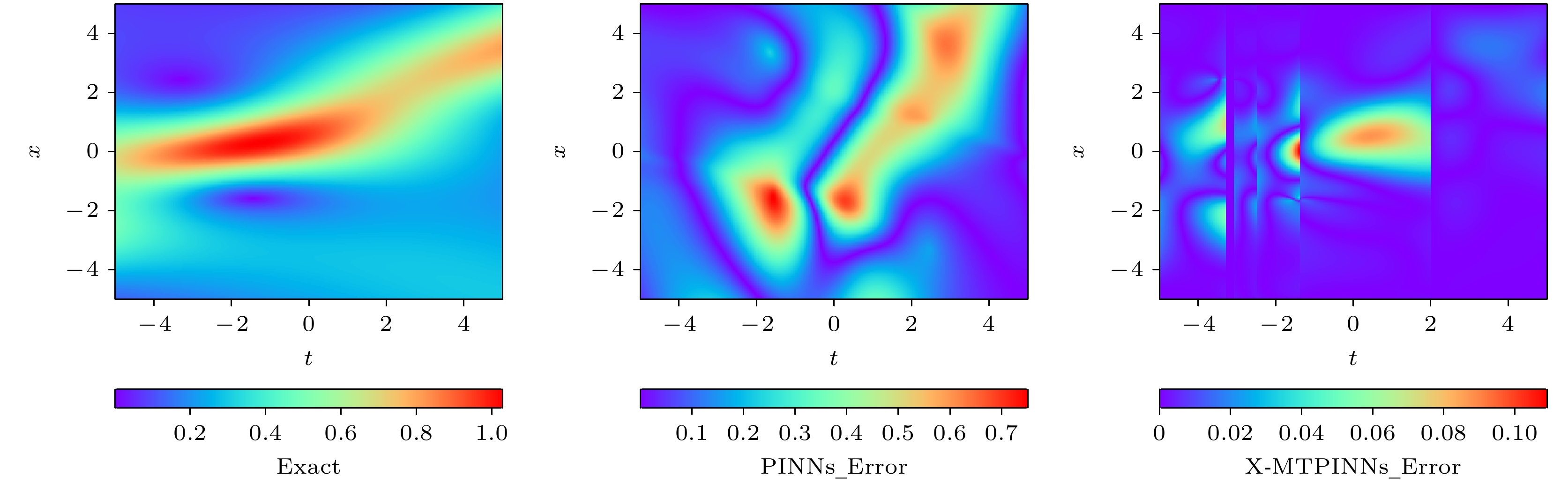
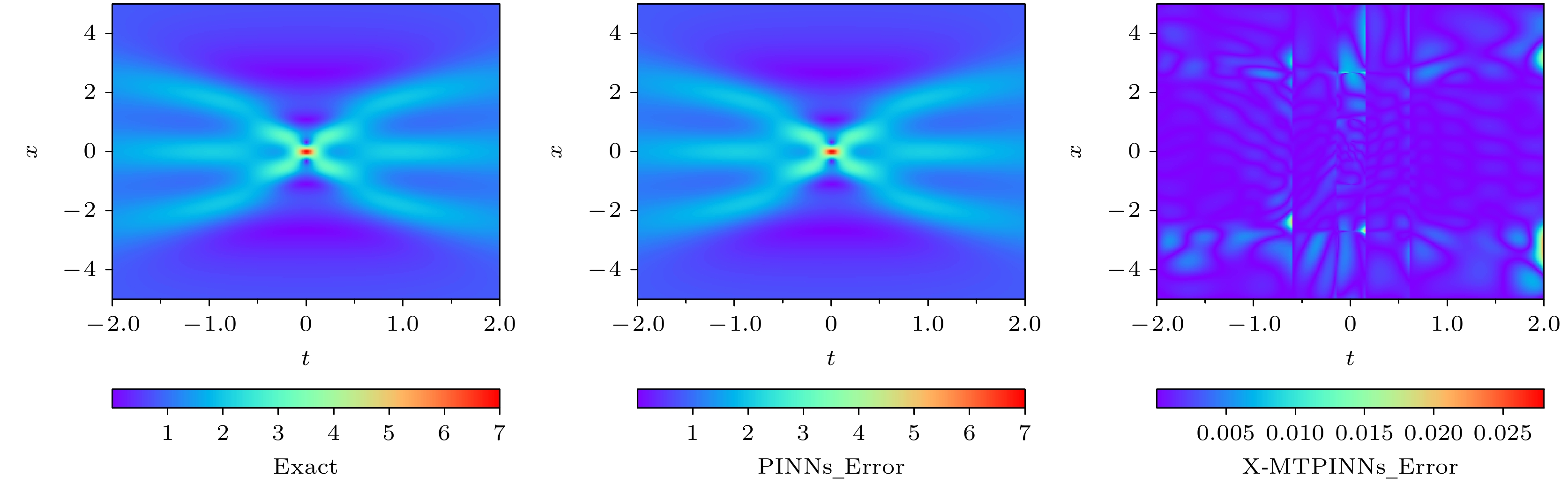
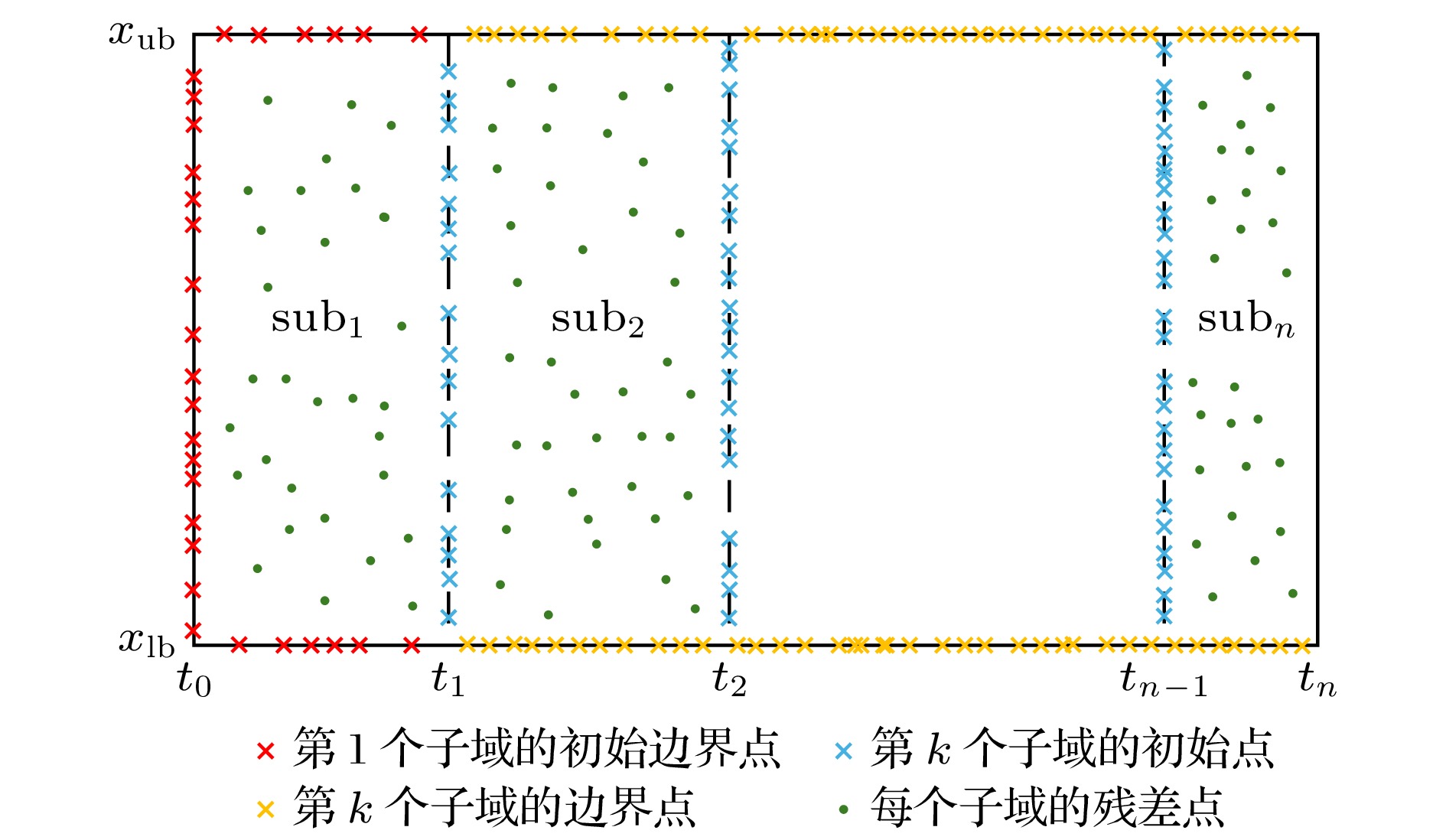
-
提出了扩展混合训练物理信息神经网络(X-MTPINNs), 该模型通过整合扩展物理信息神经网络(X-PINNs)的域分解技术与混合训练物理信息神经网络(MTPINNs)框架, 有效提升了非线性波动问题的求解能力. 相较于经典物理信息神经网络(PINNs)模型, 新模型具有双重优势: 1)混合训练框架通过优化初边值条件的处理机制, 显著改善了模型收敛特性, 在提升非线性波解拟合精度的同时, 将计算时间降低约40%; 2) X-PINNs的域分解技术增强了模型对复杂动力学行为的表征能力. 基于非线性薛定谔方程(NLSE)的数值实验表明, X-MTPINNs在亮双孤子解及三阶怪波求解以及参数反演等任务中均表现优异, 其预测精度较传统PINNs提升一至两个数量级. 对于逆问题, X-MTPINNs算法在有噪声和无噪声条件下都能准确识别NLSE中的未知参数, 解决了经典PINNs在本研究条件下NLSE参数识别中完全失效的问题, 表现出很强的鲁棒性.
-
关键词:
- 物理信息神经网络 /
- 非线性薛定谔方程 /
- 扩展混合训练物理信息神经网络 /
- 域分解 /
- 参数发现
In recent years, physics-informed neural networks (PINNs) have provided effcient data-driven methods for solving forward and inverse problems of partial differential equations (PDEs). However, when addressing complex PDEs, PINNs face significant challenges in computational efficiency and accuracy. In this study, we propose the extended mixed-training physics-informed neural networks (X-MTPINNs) as illustrated in the following figure, which effectively enhance the ability to solve nonlinear wave problems by integrating the domain decomposition technique of extended physics-informed neural networks (X-PINNs) in a mixed-training physics-informed neural networks (MTPINNs) framework. Compared with the classical PINNs model, the new model exhibits dual advantages: The first advantage is that the mixed-training framework significantly improves convergence properties by optimizing the handling mechanism of initial and boundary conditions, achieving higher fitting accuracy for nonlinear wave solutions while reducing the computation time by approximately 40%. And the second advantage is that the domain decomposition technique from X-PINNs strengthens the ability of the model to represent complex dynamical behaviors. Numerical experiments based on the nonlinear Schrödinger equation (NLSE) demonstrate that X-MTPINNs excel perform well in solving two bright solitons, third-order rogue waves, and parameter inversion tasks, with prediction accuracy improved by one to two orders of magnitude over traditional PINN. For inverse problems, the X-MTPINNs algorithm accurately identifies unknown parameters in the NLSE under noise-free, 2%, and 5% noisy conditions, solving the complete failure problem of NSLE parameter identification in classical PINNs in the studied scenario, thus demonstrating strong robustness.-
Keywords:
- physics-informed neural networks /
- nonlinear Schrödinger equation /
- extended mixed-training physics-informed neural networks /
- domain decomposition /
- parameter identification
[1] Dissanayake M, Phan-Thien N 1994 Commun. Numer. Methods Eng. 10 195
Google Scholar
[2] Lagaris I E, Likas A 1998 IEEE Trans. Neural Networks 9 987
Google Scholar
[3] Eymard R, Gallouët T, Herbin R 2000 Handb. Numer. Anal. 7 713
[4] Zhang Y 2009 Appl. Math. Comput. 215 524
[5] Taylor C A, Hughes T J R, Zarins C K 1998 Comput. Methods Appl. Mech. Eng. 158 155
Google Scholar
[6] He K M, Zhang X Y, Ren S Q, Sun J 2016 CPRV 2016-December 770
[7] Ding Y, Li J T, Zhang J X, Li P P, Bai H, Fang B, Fang H X, Huang K, Wang G Y, Nowell C J, Voelcker N H, Peng B, Li L, Huang W 2025 Nat. Commun. 16 743
Google Scholar
[8] Liu J, Chen Y B, Liu K, Zhao J 2018 32nd AAAI Conference on Artificial Intelligence New Orleans, Louisiana, USA, February 2–7, 2018 p4865
[9] Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686
Google Scholar
[10] Wang F J, Zhai Z, Zhao Z B, Di Y, Chen X F 2024 Nat. Commun. 15 4332
Google Scholar
[11] James D, Alireza D, Soroush A 2019 Sci. Total Environ. 912 168814
[12] Xu S F, Sun Z X, Huang R F, Guo D L, Yang G W, Ju S J 2023 AMS 39 322302
[13] Chiu P H, Wong J C, Ooi C C, Dao H 2022 Comput. Methods Appl. Mech. Eng. 395 114909
Google Scholar
[14] Yang L, Meng X H, Karniadakis G E 2021 J. Comput. Phys. 425 109913
Google Scholar
[15] Mojgani R, Balajewicz M, Hassanzadeh P 2023 Comput. Methods Appl. Mech. Eng. 404 115810
Google Scholar
[16] Jagtap A D, Karniadakis G E 2021 CEUR Workshop Proc. 296 4
[17] Che W J, Chen S C, Liu C, Zhao L C, Akhmediev N 2022 Phys. Rev. A 105 043526
Google Scholar
[18] Liu C, Chen S C, Yao X K, Akhmediev N 2022 Physica D 433 133192
Google Scholar
[19] Fang Y, Bo W B, Wang R R, Wang Y Y, Dai C Q 2022 Chaos, Solitons Fractals 165 112908
Google Scholar
[20] Li W T, Chen Y P, Zhang Z, Yang X Y, Li B 2025 Chin. Phys. Lett. 42 010202
Google Scholar
[21] Chen M, Wang Z 2023 Chin. Phys. B 32 090504
Google Scholar
[22] Li J, Chen Y 2020 Commun. Theor. Phys. 72 105005
Google Scholar
[23] Li J, Chen Y 2020 Commun. Theor. Phys. 72 115003
Google Scholar
[24] Song J, Zhong M, Karniadakis G E, Yan Z Y 2024 J. Comput. Phys. 505 112917
Google Scholar
[25] Wang X L, Wu Z K, Song J, Han W J, Yan Z Y 2024 Chaos, Solitons Fractals 180 114509
Google Scholar
[26] Qiu T W, Wei G M, Song Y X, Wang Z 2025 Appl. Math. Mech. 46 105
Google Scholar
[27] 田十方, 李彪 2023 72 100202
Google Scholar
Tian S F, Li B 2023 Acta Phys. Sin. 72 100202
Google Scholar
[28] Li J H, Li B 2022 Chaos, Solitons Fractals 164 112712
Google Scholar
[29] Tian S F, Li B, Zhang Z 2024 Chin. Phys. Lett. 41 030201
Google Scholar
[30] Zhou H J, Pu J C, Chen Y 2023 Nonlinear Dyn. 111 14667
Google Scholar
[31] Qiu W X, Si Z Z, Mou D S, Dai C Q, Li J T, Liu W 2025 Nonlinear Dyn. 113 4063
Google Scholar
[32] Liu X M, Zhang Z Y, Liu W J 2023 Chin. Phys. Lett. 40 070501
Google Scholar
[33] Liu H Y, Zhang Y B, Wang L 2024 J. Syst. Sci. 37 494
Google Scholar
[34] Zhang W X, Chen Y 2025 Nonlinear Dyn. 113 10211
Google Scholar
[35] Pu J C, Chen Y 2024 J. Comput. Phys. 510 113090
Google Scholar
[36] 张解放, 戴朝卿, 王悦悦 2016 基于非线性薛定谔方程的畸形波理论及其应用(北京: 科学出版社) 第44—63页
Zhang J F, Dai C Q, Wang Y Y 2016 Rogue Wave Theory and Its Applications Based on the Nonlinear Schrödinger Equation (Beijing: Science Press) pp44–63
-
图 2 扩展混合训练物理信息神经网络(X-MTPINNs)
Fig. 2. Extended mixed-training physics-informed neural networks (X-MTPINNs).
图 3 NLSE亮双孤子解的真实值和不同模型的预测误差
Fig. 3. Exact values of two bright solitons in the NLSE and prediction errors from different models.
图 4 NLSE三阶怪波的真实值和不同模型的预测误差
Fig. 4. Exact values of third-order rogue waves in the NLSE and prediction errors from different models.
表 1 两种模型对NLSE亮双孤子解的数值预测结果
Table 1. Numerical prediction results of two models for two bright solitons in the NLSE
亮双孤子 子域 隐藏
层数神经
元数L2误差 训练时间/s X-
MTPINNs[–5.00, –3.30] 4 50 4.52×10–2 2531.88 [–3.30, –2.50] 4 50 2.63×10–2 2459.23 [–2.50, –1.40] 4 50 3.03×10–2 2347.56 [–1.40, 2.00] 4 50 5.73×10–2 2489.87 [2.00, 5.00] 4 50 1.70×10–2 2489.87 Global [–5, 5] 4 50 3.38×10–2 2531.88 PINNs [–5, 5] 4 50 2.51×10–1 4176.69 
下载: 导出CSV
表 2 两种模型对非线性薛定谔方程三阶怪波的数值预测结果
Table 2. Numerical prediction results of third-order rogue waves in the NLSE
三阶怪波 子域 隐藏
层数神经
元数L2误差 训练时间/s X-
MTPINNs[–2.00, –0.60] 4 50 1.25×10–3 3065.07 [–0.60, –0.15] 4 50 1.22×10–3 2228.26 [–0.15, 0.15] 4 50 3.89×10–3 2018.29 [0.15, 0.60] 4 50 1.31×10–3 2438.84 [0.60, 2.00] 4 50 1.84×10–3 2339.57 Global [–2, 2] 4 50 2.25×10–3 3065.07 PINNs [–2, 2] 4 50 4.94×10–1 5538.17
下载: 导出CSV
表 3 通过学习所得的$ \lambda_1 $和$ \lambda_2 $及其误差
Table 3. Learned $ \lambda_1 $ and $ \lambda_2 $ and their associated errors
NPDEs 噪声 非线性演化方程 相对误差$ [\lambda_1, \lambda_2] $/% Correct — $ {\rm{i}}\hat{h}_t + 0.5\hat{h}_{xx} + |\hat{h}|^2\hat{h} = 0 $ $ [0, 0] $ [–2.00, –0.60] 0% $ \lambda_1 = 0.4999224, \lambda_2 = 0.9999491 $ $ [0.01553, 0.00509] $ 2% $ \lambda_1 = 0.5006779, \lambda_2 = 1.0010909 $ $ [0.13558, 0.10909] $ 5% $ \lambda_1 = 0.5017547, \lambda_2 = 1.0026274 $ $ [0.35094, 0.26274] $ [–0.60, –0.08] 0% $ \lambda_1 = 0.4995355, \lambda_2 = 0.9997470 $ $ [0.09289, 0.02530] $ 2% $ \lambda_1 = 0.4990919, \lambda_2 = 0.9979020 $ $ [0.18162, 0.20980] $ 5% $ \lambda_1 = 0.4983062, \lambda_2 = 0.9952767 $ $ [0.33876, 0.47233] $ [–0.08, 0.00] 0% $ \lambda_1 = 0.4907891, \lambda_2 = 0.9970491 $ $ [1.84218, 0.29509] $ 2% $ \lambda_1 = 0.4856022, \lambda_2 = 0.9931418 $ $ [2.87955, 0.68582] $ 5% $ \lambda_1 = 0.4838027, \lambda_2 = 0.9913622 $ $ [3.23946, 0.86378] $ [0.00, 0.08] 0% $ \lambda_1 = 0.4978686, \lambda_2 = 0.9941696 $ $ [0.42627, 0.58304] $ 2% $ \lambda_1 = 0.4953954, \lambda_2 = 0.9936743 $ $ [0.92092, 0.63257] $ 5% $ \lambda_1 = 0.4909737, \lambda_2 = 0.9887489 $ $ [1.80527, 1.12511] $ [0.08, 0.60] 0% $ \lambda_1 = 0.4999007, \lambda_2 = 0.9997627 $ $ [0.01987, 0.02373] $ 2% $ \lambda_1 = 0.4997132, \lambda_2 = 0.9992683 $ $ [0.05737, 0.07317] $ 5% $ \lambda_1 = 0.4974256, \lambda_2 = 0.9973150 $ $ [0.51489, 0.26850] $ [0.60, 2.00] 0% $ \lambda_1 = 0.5002598, \lambda_2 = 1.0001861 $ $ [0.05195, 0.01861] $ 2% $ \lambda_1 = 0.4997032, \lambda_2 = 0.9999705 $ $ [0.05936, 0.00295] $ 5% $ \lambda_1 = 0.4995049, \lambda_2 = 0.9998789 $ $ [0.09903, 0.01211] $ Global 0% $ \lambda_1 = 0.972926, \lambda_2 = 0.9987469 $ $ [0.54148, 0.12531] $ 2% $ \lambda_1 = 0.5035173, \lambda_2 = 0.9971460 $ $ [0.70345, 0.28540] $ 5% $ \lambda_1 = 4.9470665, \lambda_2 = 1.0050076 $ $ [1.05867, 0.50076] $
下载: 导出CSV
-
[1] Dissanayake M, Phan-Thien N 1994 Commun. Numer. Methods Eng. 10 195
Google Scholar
[2] Lagaris I E, Likas A 1998 IEEE Trans. Neural Networks 9 987
Google Scholar
[3] Eymard R, Gallouët T, Herbin R 2000 Handb. Numer. Anal. 7 713
[4] Zhang Y 2009 Appl. Math. Comput. 215 524
[5] Taylor C A, Hughes T J R, Zarins C K 1998 Comput. Methods Appl. Mech. Eng. 158 155
Google Scholar
[6] He K M, Zhang X Y, Ren S Q, Sun J 2016 CPRV 2016-December 770
[7] Ding Y, Li J T, Zhang J X, Li P P, Bai H, Fang B, Fang H X, Huang K, Wang G Y, Nowell C J, Voelcker N H, Peng B, Li L, Huang W 2025 Nat. Commun. 16 743
Google Scholar
[8] Liu J, Chen Y B, Liu K, Zhao J 2018 32nd AAAI Conference on Artificial Intelligence New Orleans, Louisiana, USA, February 2–7, 2018 p4865
[9] Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686
Google Scholar
[10] Wang F J, Zhai Z, Zhao Z B, Di Y, Chen X F 2024 Nat. Commun. 15 4332
Google Scholar
[11] James D, Alireza D, Soroush A 2019 Sci. Total Environ. 912 168814
[12] Xu S F, Sun Z X, Huang R F, Guo D L, Yang G W, Ju S J 2023 AMS 39 322302
[13] Chiu P H, Wong J C, Ooi C C, Dao H 2022 Comput. Methods Appl. Mech. Eng. 395 114909
Google Scholar
[14] Yang L, Meng X H, Karniadakis G E 2021 J. Comput. Phys. 425 109913
Google Scholar
[15] Mojgani R, Balajewicz M, Hassanzadeh P 2023 Comput. Methods Appl. Mech. Eng. 404 115810
Google Scholar
[16] Jagtap A D, Karniadakis G E 2021 CEUR Workshop Proc. 296 4
[17] Che W J, Chen S C, Liu C, Zhao L C, Akhmediev N 2022 Phys. Rev. A 105 043526
Google Scholar
[18] Liu C, Chen S C, Yao X K, Akhmediev N 2022 Physica D 433 133192
Google Scholar
[19] Fang Y, Bo W B, Wang R R, Wang Y Y, Dai C Q 2022 Chaos, Solitons Fractals 165 112908
Google Scholar
[20] Li W T, Chen Y P, Zhang Z, Yang X Y, Li B 2025 Chin. Phys. Lett. 42 010202
Google Scholar
[21] Chen M, Wang Z 2023 Chin. Phys. B 32 090504
Google Scholar
[22] Li J, Chen Y 2020 Commun. Theor. Phys. 72 105005
Google Scholar
[23] Li J, Chen Y 2020 Commun. Theor. Phys. 72 115003
Google Scholar
[24] Song J, Zhong M, Karniadakis G E, Yan Z Y 2024 J. Comput. Phys. 505 112917
Google Scholar
[25] Wang X L, Wu Z K, Song J, Han W J, Yan Z Y 2024 Chaos, Solitons Fractals 180 114509
Google Scholar
[26] Qiu T W, Wei G M, Song Y X, Wang Z 2025 Appl. Math. Mech. 46 105
Google Scholar
[27] 田十方, 李彪 2023 72 100202
Google Scholar
Tian S F, Li B 2023 Acta Phys. Sin. 72 100202
Google Scholar
[28] Li J H, Li B 2022 Chaos, Solitons Fractals 164 112712
Google Scholar
[29] Tian S F, Li B, Zhang Z 2024 Chin. Phys. Lett. 41 030201
Google Scholar
[30] Zhou H J, Pu J C, Chen Y 2023 Nonlinear Dyn. 111 14667
Google Scholar
[31] Qiu W X, Si Z Z, Mou D S, Dai C Q, Li J T, Liu W 2025 Nonlinear Dyn. 113 4063
Google Scholar
[32] Liu X M, Zhang Z Y, Liu W J 2023 Chin. Phys. Lett. 40 070501
Google Scholar
[33] Liu H Y, Zhang Y B, Wang L 2024 J. Syst. Sci. 37 494
Google Scholar
[34] Zhang W X, Chen Y 2025 Nonlinear Dyn. 113 10211
Google Scholar
[35] Pu J C, Chen Y 2024 J. Comput. Phys. 510 113090
Google Scholar
[36] 张解放, 戴朝卿, 王悦悦 2016 基于非线性薛定谔方程的畸形波理论及其应用(北京: 科学出版社) 第44—63页
Zhang J F, Dai C Q, Wang Y Y 2016 Rogue Wave Theory and Its Applications Based on the Nonlinear Schrödinger Equation (Beijing: Science Press) pp44–63
下载:
计量
- 文章访问数: 514
- PDF下载量: 11
- 被引次数: 0
