-
非线性薛定谔方程(NLSE)在量子力学、非线性光学、等离子体物理、凝聚态物理、光纤通信和激光系统设计等多个领域中都具有重要的应用, 其精确求解对于理解复杂物理现象至关重要. 本文深入研究了传统的有限差分法(FDM)、分步傅里叶法(SSF)与智能算法中的物理信息神经网络(PINN)方法, 旨在高效且准确地求解光纤中的复杂NLSE. 首先介绍了PINN方法对NLSE的求解方法、步骤和结果, 并对比了FDM, SSF, PINN方法对复杂NLSE求解与脉冲远距离脉冲传输的误差. 然后, 讨论了PINN不同网络结构和网络参数对NLSE求解精度的影响, 还验证了集成学习策略的有效性, 即通过结合传统数值方法与PINN的优势, 提高NLSE求解的准确度. 最后, 采用上述算法研究了不同啁啾的艾里脉冲在光纤中的演化过程与保偏光纤对应的矢量非线性薛定谔方程(VNLSE)求解过程及结果误差. 本研究通过对比FDM, SSF, PINN在求解NLSE时的特点, 提出的集成学习方案在脉冲传输动力学研究和数据驱动仿真方面具有重要的应用.Nonlinear Schrödinger equation (NLSE) has important applications in quantum mechanics, nonlinear optics, plasma physics, condensed matter physics, optical fiber communication and laser system design, and its accurate solution is very important for understanding complex physical phenomena. Here, the traditional finite difference method (FDM), the split-step Fourier (SSF) method and the physics-informed neural network (PINN) method are studied, aiming to analyze in depth the solving mechanisms of various algorithms, and then realize the efficient and accurate solution of complex NLSE in optical fiber. Initially, the steps, process and results of PINN in solving the NLSE for pulse under the condition of short-distance transmission are described, and the errors of these methods are quantitatively evaluated by comparing them with the errors of PINN, FDM and SSF. On this basis, the key factors affecting the accuracy of NLSE solution for pulse under long-distance transmission are further discussed. Then, the effects of different networks, activation functions, hidden layers and the number of neurons in PINN on the accuracy of NLSE solution are discussed. It is found that selecting a suitable combination of activation functions and network types can significantly reduce the error, and the combination of FNN and tanh activation functions is particularly good. The effectiveness of ensemble learning strategy is also verified, that is, by combining the advantages of traditional numerical methods and PINN, the accuracy of NLSE solution is improved. Finally, the evolution characteristics of Airy pulse with different chirps in fiber and the solution of vector NLSE corresponding to polarization-maintaining fiber are studied by using the above algorithm. This study explores the solving mechanisms of FDM, SSF and PINN in complex NLSE, compares and analyzes the error characteristics of those methods in various transmission scenarios, proposes and verifies the ensemble learning strategy, thus providing a solid theoretical basis for studying pulse transmission dynamics and data-driven simulation.
-
Keywords:
- pulse transmission in fiber /
- nonlinear Schrödinger equation /
- physical information neural network /
- Airy chirp pulse
[1] 阿戈沃 G P著 (贾东方, 余震虹 译) 2010 非线性光纤光学原理及应用 (北京: 电子工业出版社) 第18—109页
Agrawal G P (translated by Jia D F, Yu Z H) 2010 Principles and Applications of Nonlinear Fibre Optics (Beijing: Electronic Industry Press) pp18–109
[2] Ngo N Q 2018 Ultra-fast Fiber Lasers: Principles and Applications with MATLAB® Models (Boca Raton: CRC Press) pp139–157
[3] Chang Q S, Jia E H, Sun W 1999 J. Comput. Phys. 148 397
Google Scholar
[4] Wang H Q 2005 Appl. Math. Comput. 170 17
Google Scholar
[5] 赵磊, 隋展, 朱启华, 张颖, 左言磊 2009 58 3977
Google Scholar
Zhao L, Sui Z, Zhu Q H, Zhang Y, Zuo Y L 2009 Acta Phys. Sin. 58 3977
Google Scholar
[6] Xie S S, Li G X, Yi S 2009 Comput. Meth. Appl. Mech. Eng. 198 1052
Google Scholar
[7] Wu L 2012 Numer. Meth. Partial Differ. Eq. 28 63
Google Scholar
[8] Caplan R M 2013 Appl. Numer. Math. 71 24
Google Scholar
[9] 崔少燕, 吕欣欣, 辛杰 2016 65 040201
Google Scholar
Cui S Y, Lv X X, Xin J 2016 Acta Phys. Sin. 65 040201
Google Scholar
[10] Feng X B, Li B Y, Ma S 2021 SIAM J. Numer. Anal. 59 1566
Google Scholar
[11] Ibarra-Villalón H E, Pottiez O, Gómez-Vieyra A, Lauterio-Cruz J P, Bracamontes- Rodriguez Y E 2023 Phys. Scr. 98 065514
Google Scholar
[12] Zhang L F, Liu K, Zhong H Z, Zhang J G, Li Y, Fan D Y 2015 Opt. Express 23 2566
Google Scholar
[13] Yu Y, Zhang Y T, Song X X, Zhang H T, Cao M X, Che Y L, Zhang H, Yao J Q 2017 IEEE Photonics J. 9 7904107
Google Scholar
[14] Xin W, Wang Y, Xin Z G, Li L 2021 Opt. Commun. 489 126889
Google Scholar
[15] 罗民, 张泽贤, 陈乃妙, 刘萌, 罗爱平, 徐文成, 罗智超 2023 72 204203
Google Scholar
Luo M, Zhang Y Z, Chen N M, Liu M, Luo A P, Xu W C, Luo Z C 2023 Acta Phys. Sin. 72 204203
Google Scholar
[16] Lawal Z K, Yassin H, Lai D T, Che-Idris A 2022 Big Data Cogn. Comput. 6 140
Google Scholar
[17] Karniadakis G E, Kevrekidis I G, Lu L, Perdikaris P, Wang S, Yang L 2021 Nat. Rev. Phys. 3 422
Google Scholar
[18] 李野, 陈松灿 2022 计算机科学 49 254
Google Scholar
Li Y, Chen S C 2022 Comput. Sci. 49 254
Google Scholar
[19] Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686
Google Scholar
[20] Pu J C, Peng W Q, Chen Y 2021 Wave Motion. 107 102823
Google Scholar
[21] Pu J C, Li J, Chen Y 2021 Nonlinear Dyn. 105 1723
Google Scholar
[22] Wang L, Yan Z Y 2021 Phys. Lett. A 404 127408
Google Scholar
[23] Zang Y B, Yu Z M, Xu K, Chen M H, Yang S G, Chen H W 2021 J. Lightwave Technol. 40 404
Google Scholar
[24] Jiang X T, Wang D S, Chen X, Zhang M 2022 J. Lightwave Technol. 40 21
Google Scholar
[25] Jiang X T, Wang D S, Fan Q R, Zhang M, Lu C, Lau A P 2022 Laser Photonics Rev. 16 2100483
Google Scholar
[26] Fang Y, Bo W B, Wang R R, Wang W W, Chao Q D 2022 Chaos Soliton. Fract. 165 112908
Google Scholar
[27] 田十方, 李彪 2023 72 100202
Google Scholar
Tian S F, Li B 2023 Acta Phys. Sin. 72 100202
Google Scholar
[28] 罗霄, 张民, 蒋啸天, 宋裕琛, 张希萌, 王丹石 2023 红外与激光工程 52 12
Google Scholar
Luo X, Zhang M, Jiang X T, Song X M, Zhang X M, Wang D S 2023 Infrared Laser Eng. 52 12
Google Scholar
[29] Thulasidharan K, Sinthuja N, Priya N V, Senthilvelan M 2024 Commun. Theor. Phys. 76 115801
Google Scholar
[30] Psaros A F, Kawaguchi K, Karniadakis G E 2022 J. Comput. Phys. 458 111121
Google Scholar
[31] Uduagbomen J, Leeson M S, Liu Z, Lakshminarayana S, Xu T H 2024 Appl. Opt. 63 3794
Google Scholar
[32] Cuomo S, Di Cola V S, Giampaolo F, Rozza G, Raissi M, Piccialli F 2022 J. Sci. Comput. 92 88
Google Scholar
[33] Lu L, Meng X H, Mao Z P, Karniadakis G E 2019 SIAM Rev. 63 208
Google Scholar
[34] Yu J, Lu L, Meng X H, Karniadakis G E 2022 Comput. Methods Appl. Mech. Eng. 393 114823
Google Scholar
[35] Wang T M, Cai L J, Xia C J, Song H, Li L B, Bai G X, Fu N Q, Xian L D, Yang R, Mu H R, Zhang G Y, Lin S H 2024 Adv. Sci. 11 2406476
Google Scholar
[36] Gong K W, Li L B, Yu W Z 2023 Mater. Des. 228 111848
Google Scholar
[37] Ding B B, Li L B, Gong K W 2023 Appl. Surf. Sci. 22 156944
Google Scholar
[38] Mao D, He Z W, Zhang Y S, Du Y Q, Zeng C, Yun L, Luo Z C, Li T J, Sun Z P, Zhao J L 2022 Light Sci. Appl. 11 25
Google Scholar
[39] Mao D, Wang H, Zhang H, Zeng C, Du Y Q, He Z W, Sun Z P, Zhao J L 2021 Nat. Commun. 12 6712
Google Scholar
[40] Mao D, Gao Q, Li J Y, He Z W, Du Y Q, Zeng C, Sun Z P, Zhao J L 2022 Phys. Rev. Appl. 18 044044
Google Scholar
[41] Rao C P, Ren P, Wang Q, Buyukozturk O, Sun H, Liu Y 2023 Nat. Mach. Intell. 5 765
Google Scholar
[42] Cao R H, Su J, Feng J Q, Guo Q 2024 Electron. Res. Arch. 32 6641
Google Scholar
[43] Ismail M S, Alamri S Z 2004 Int. J. Comput. Math. 81 333
Google Scholar
[44] Wang T 2011 J. Comput. Appl. Math. 235 4237
Google Scholar
[45] Wu G Z, Fang Y, Wang Y Y, Wu G C, Dai C Q 2021 Chaos Solitons Fractals 152 111393
Google Scholar
-
图 1 基于NLSE的脉冲在光纤中传输方程的FDM, SSF, PINN三种方法求解示意图
Fig. 1. Schematic diagram of FDM, SSF, PINN methods for solving the propagation equation of pulses in optical fibers based on NLSE.
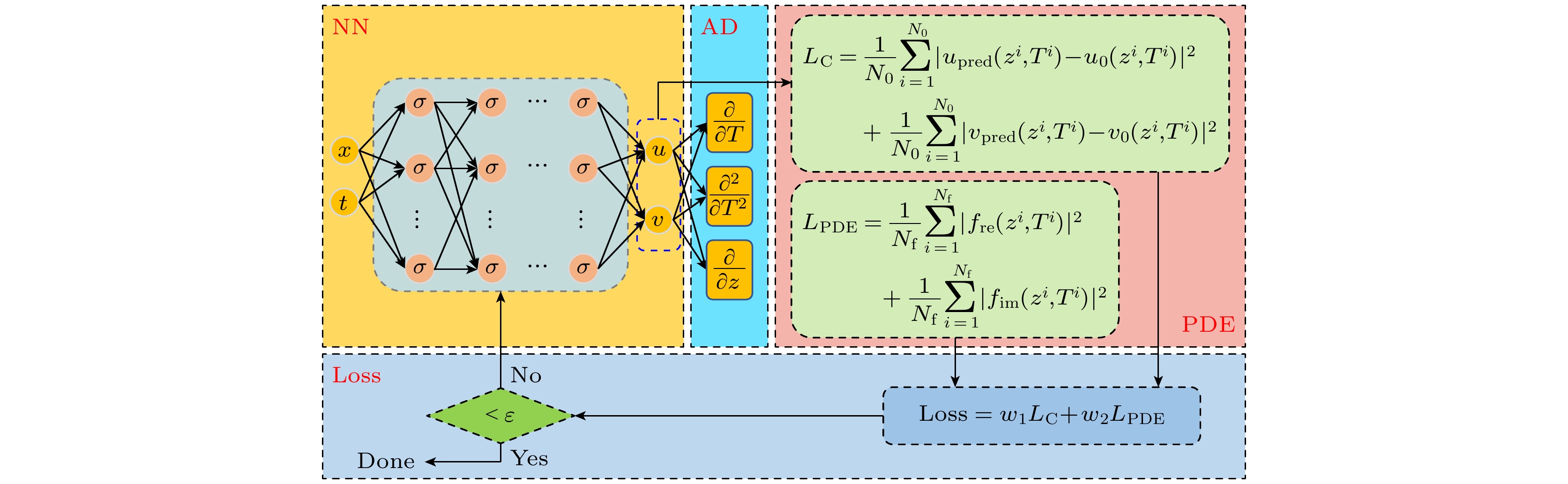
图 2 基于PINN的NLSE求解示意图, 其中NN为神经网络, AD为自动微分技术, PDE为NLSE实虚部分离对应的物理信息, Loss为优化物理信息损失函数
Fig. 2. Schematic diagram of NLSE solution based on PINN. NN is the neural network, AD is the automatic differentiation technology, PDE is the physical information corresponding to the real and imaginary part of the NLSE, Loss is the optimized physical information loss function.
图 3 基于PINN的NLSE求解结果 (a) 脉冲在光纤中的传播演化图; (b) 损失函数曲线
Fig. 3. Results of NLSE solving by PINN: (a) Evolution diagram of pulse propagation in fiber; (b) loss function curves.
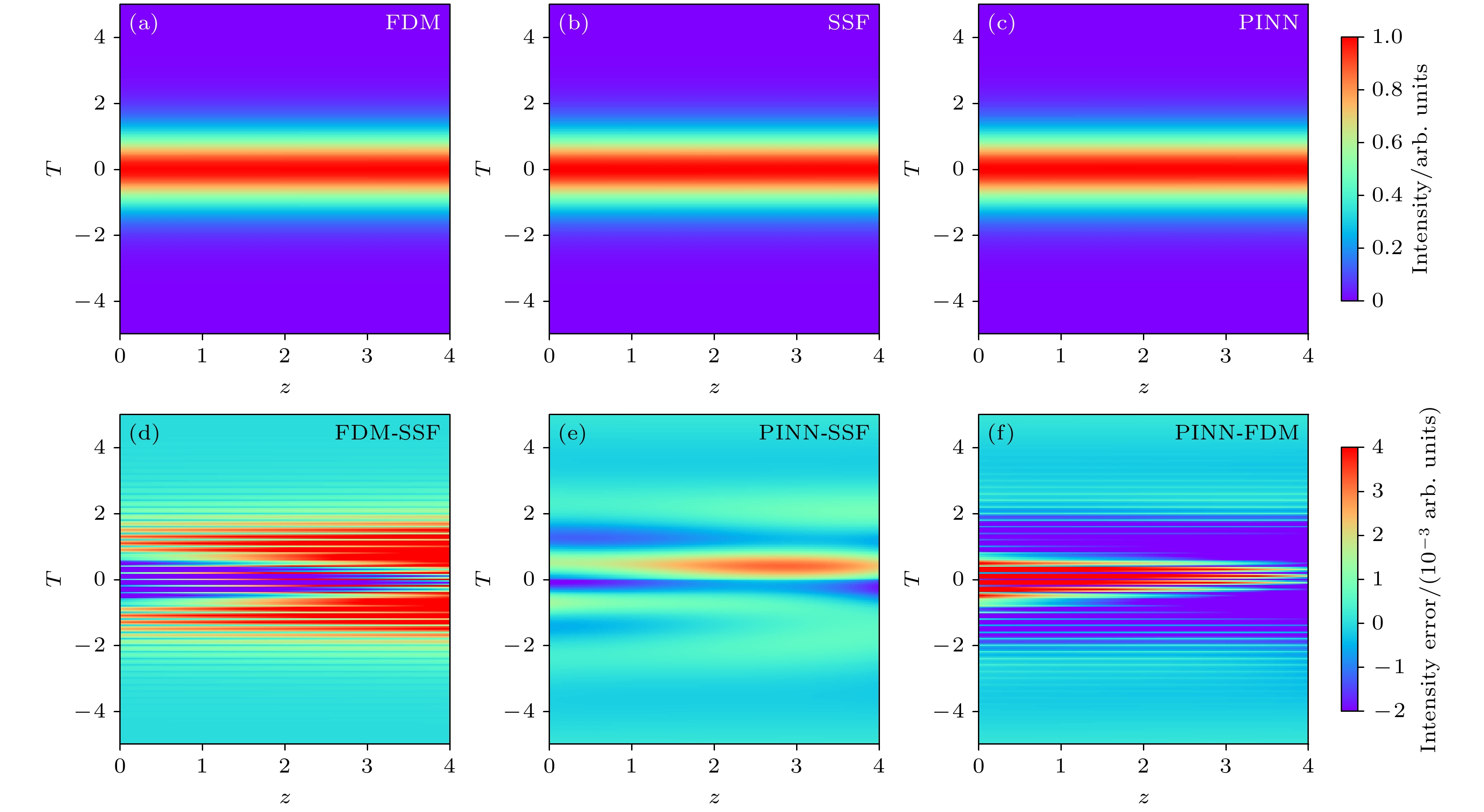
图 4 多种算法对复杂NLSE求解的脉冲演化过程和对比图 (a) FDM求解的脉冲在光纤中的传播演化图; (b) SSF求解的脉冲在光纤中的传播演化图; (c) PINN求解对应的脉冲在光纤中的传播演化图; (d) FDM与SSF之间的交叉对比图; (e) PINN与SSF之间的交叉对比图; (f) PINN与FDM之间的交叉对比图
Fig. 4. Pulse evolution process and comparison diagram of FDM, SSF and PINN: (a) Pulse evolution process based on FDM; (b) pulse evolution process based on SSF; (c) pulse evolution process based on PINN; (d) comparison diagram between FDM and SSF; (e) comparison diagram between PINN and SSF; (f) comparison diagram between PINN and FDM.
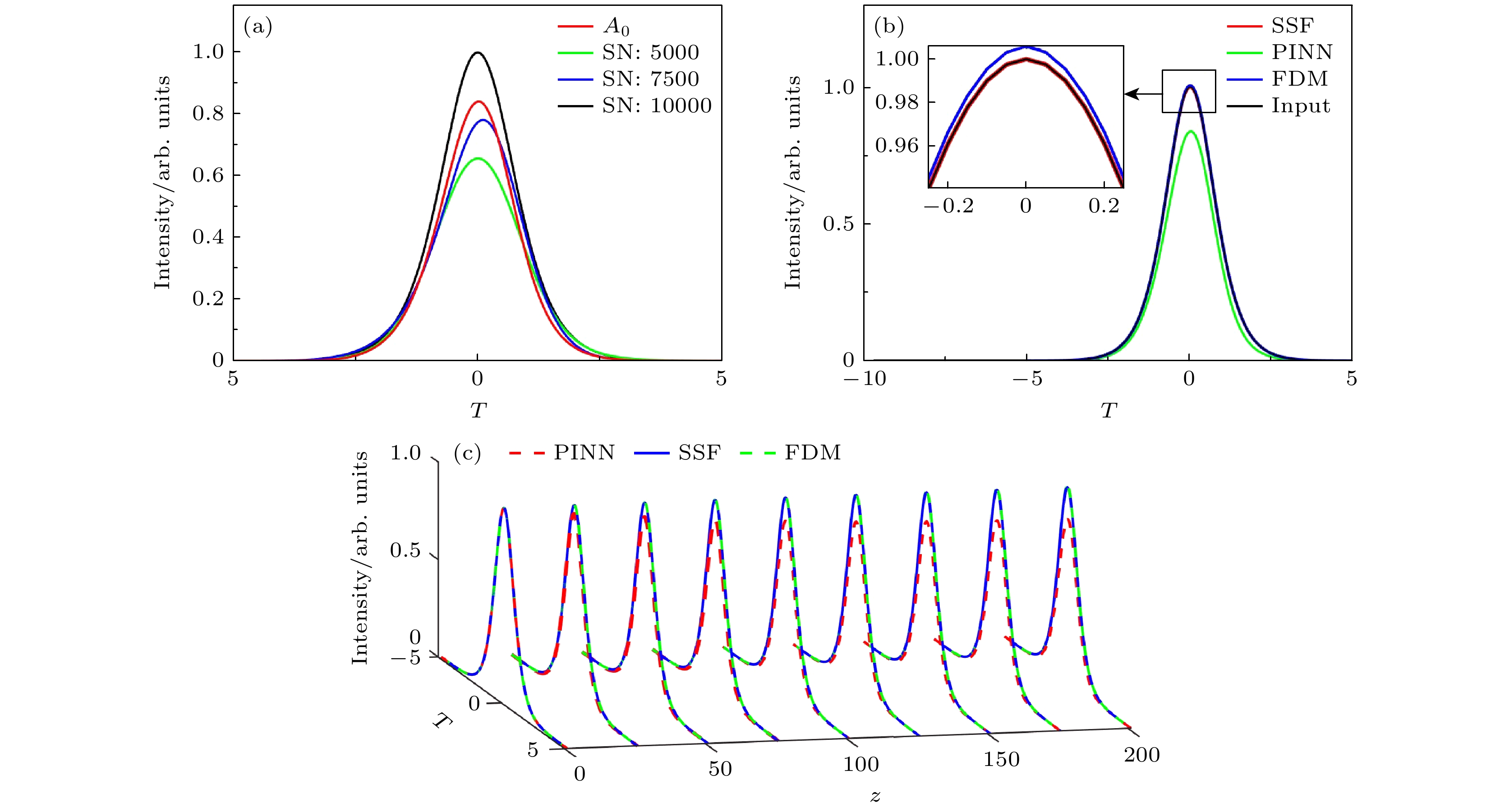
图 5 PINN, SSF, FDM求解基阶孤子在200 m光纤中传输的结果 (a) PINN在不同采样点数下的输入与输出对比图; (b) FDM, SSF, PINN求解的输入与输出对比图; (c) FDM, SSF, PINN求解的基阶孤子传输演化图
Fig. 5. Results of PINN, SSF, and FDM solving the fundamental order soliton transmission in a 200 m fiber: (a) Results of PINN at different sampling number (SN); (b) results of FDM, SSF, PINN and input; (c) evolution of fundamental soliton transmission solved by FDM, SSF and PINN.
图 6 不同激活函数与神经网络设置下PINN的训练误差图 (a) 神经网络为FNN, 激活函数为Tanh的训练误差图; (b) 神经网络为FNN, 激活函数为Sigmoid的训练误差图; (c) 神经网络为FNN, 激活函数为Swish的训练误差图; (d) 神经网络为PFNN, 激活函数为Tanh的训练误差图; (e) 神经网络为PFNN, 激活函数为Sigmoid的训练误差图; (f) 神经网络为PFNN, 激活函数为Swish的训练误差图
Fig. 6. Training error of PINN under different activation function and NN: (a) Training error with Tanh and FNN; (b) training error with Sigmoid and FNN; (c) training error with Swish and FNN; (d) training error with Tanh and PFNN; (e) training error with Sigmoid and PFNN; (f) training error with Swish and PFNN.
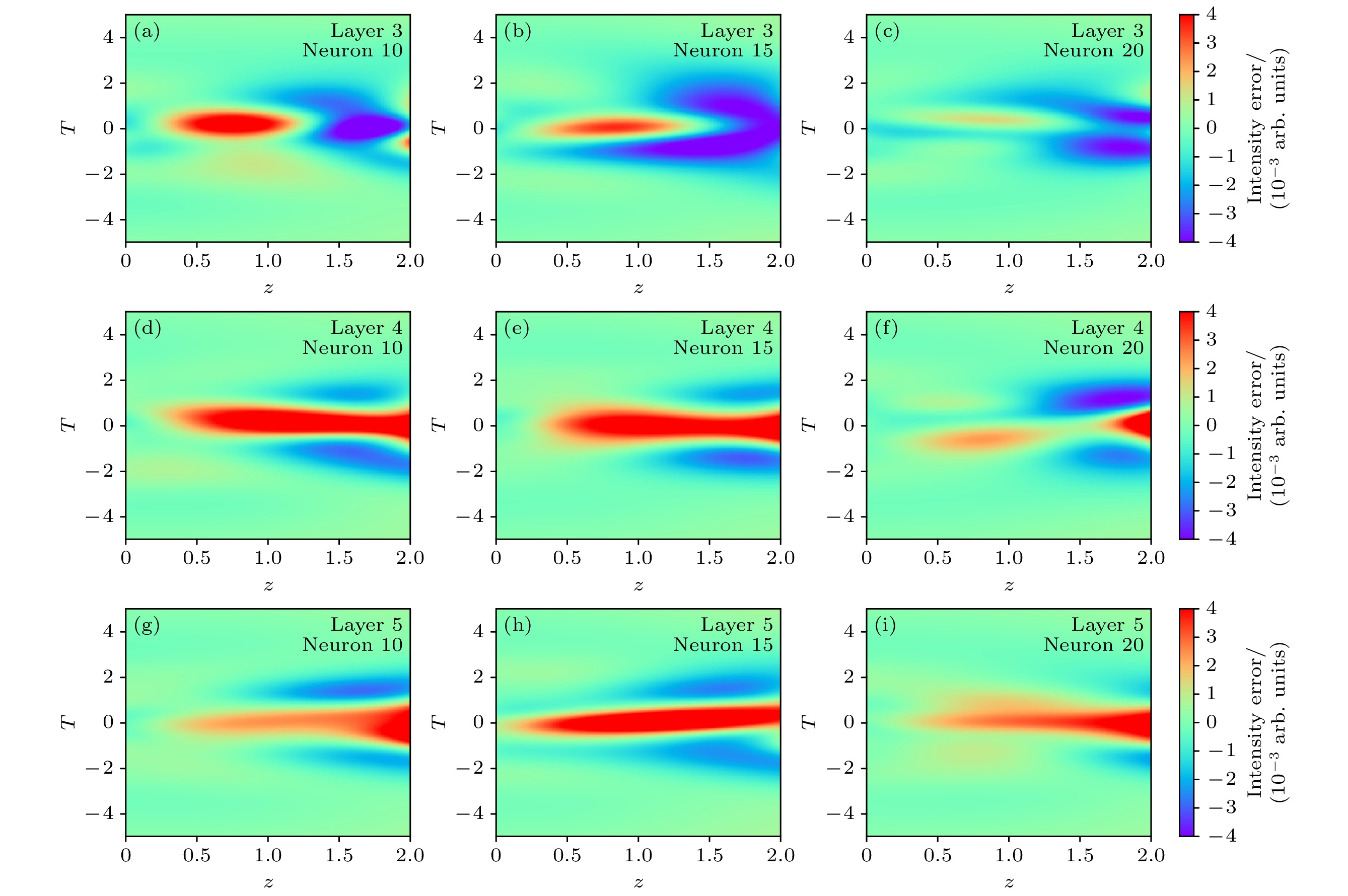
图 7 不同隐藏层和神经元设置下PINN训练误差图 (a) 隐藏层为3, 神经元为10的训练误差图; (b) 隐藏层为3, 神经元为15的训练误差图; (c) 隐藏层为3, 神经元为20的训练误差图; (d)隐藏层为4, 神经元为10的训练误差图; (e) 隐藏层为4, 神经元为15的训练误差图; (f) 隐藏层为4, 神经元为20的训练误差图; (g) 隐藏层为5, 神经元为10的训练误差图; (h) 隐藏层为5, 神经元为15的训练误差图; (i) 隐藏层为5, 神经元为20的训练误差图
Fig. 7. Training error of PINN under different number of hidden layers and neurons: (a) Training error with 3 and 10; (b) training error with 3 and 15; (c) training error with 3 and 20; (d) training error with 4 and 10; (e) training error with 4 and 15; (f) training error with 4 and 20; (g) training error with 5 and 10; (h) training error with 5 and 15; (i) training error with 5 and 20.
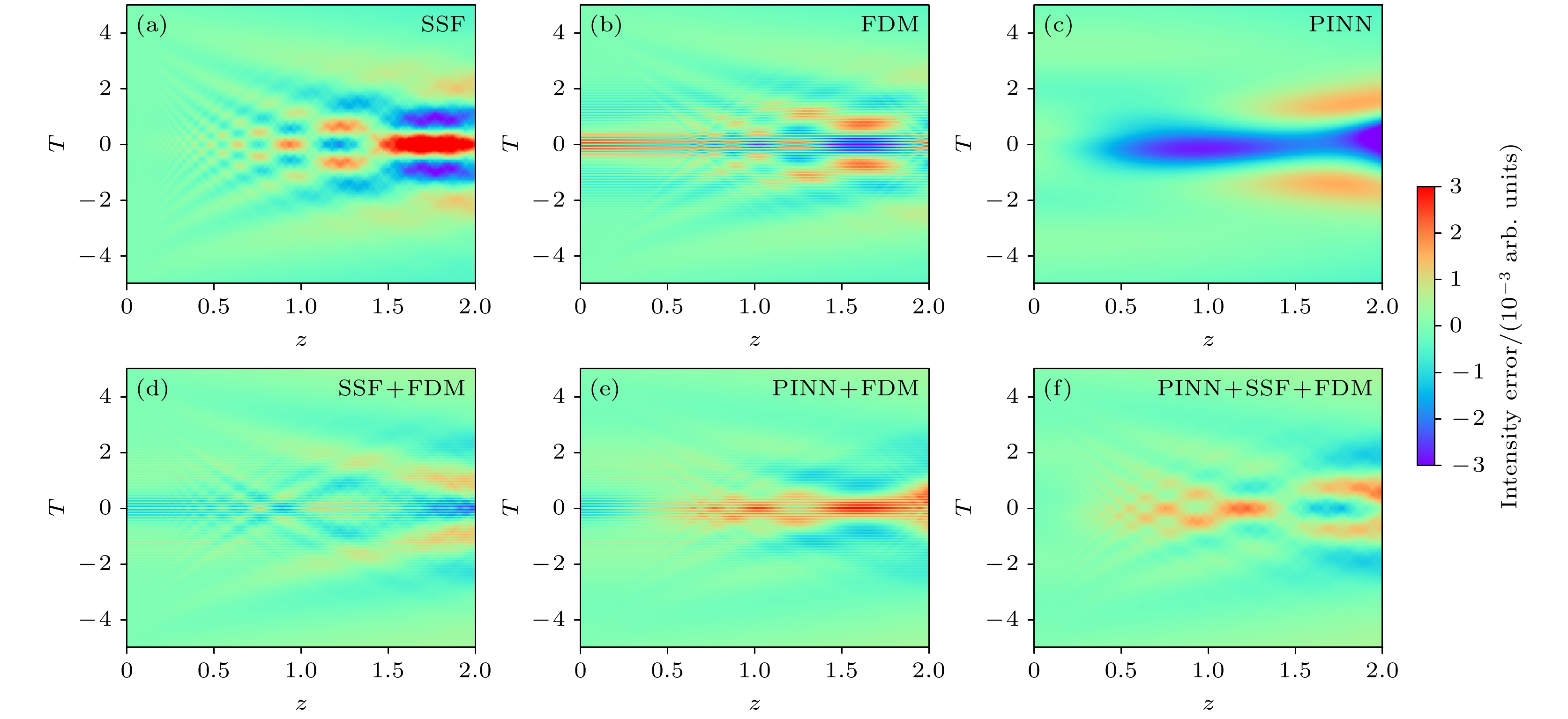
图 8 不同集成方式对所得结果误差的影响 (a)—(c)分别为SSF, FDM, PINN求解的脉冲传输与解析解误差; (d)—(f)分别为SSF+FDM, PINN+FDM, PINN+SSF+FDM集成求解的脉冲传输与解析解误差
Fig. 8. Influence of different integration methods on the results’ error: (a)–(c) The pulse transmission and errors of SSF, FDM and PINN solutions; (d)–(f) the pulse transmission and errors of SSF+FDM, PINN+FDM and PINN+SSF+FDM solutions.
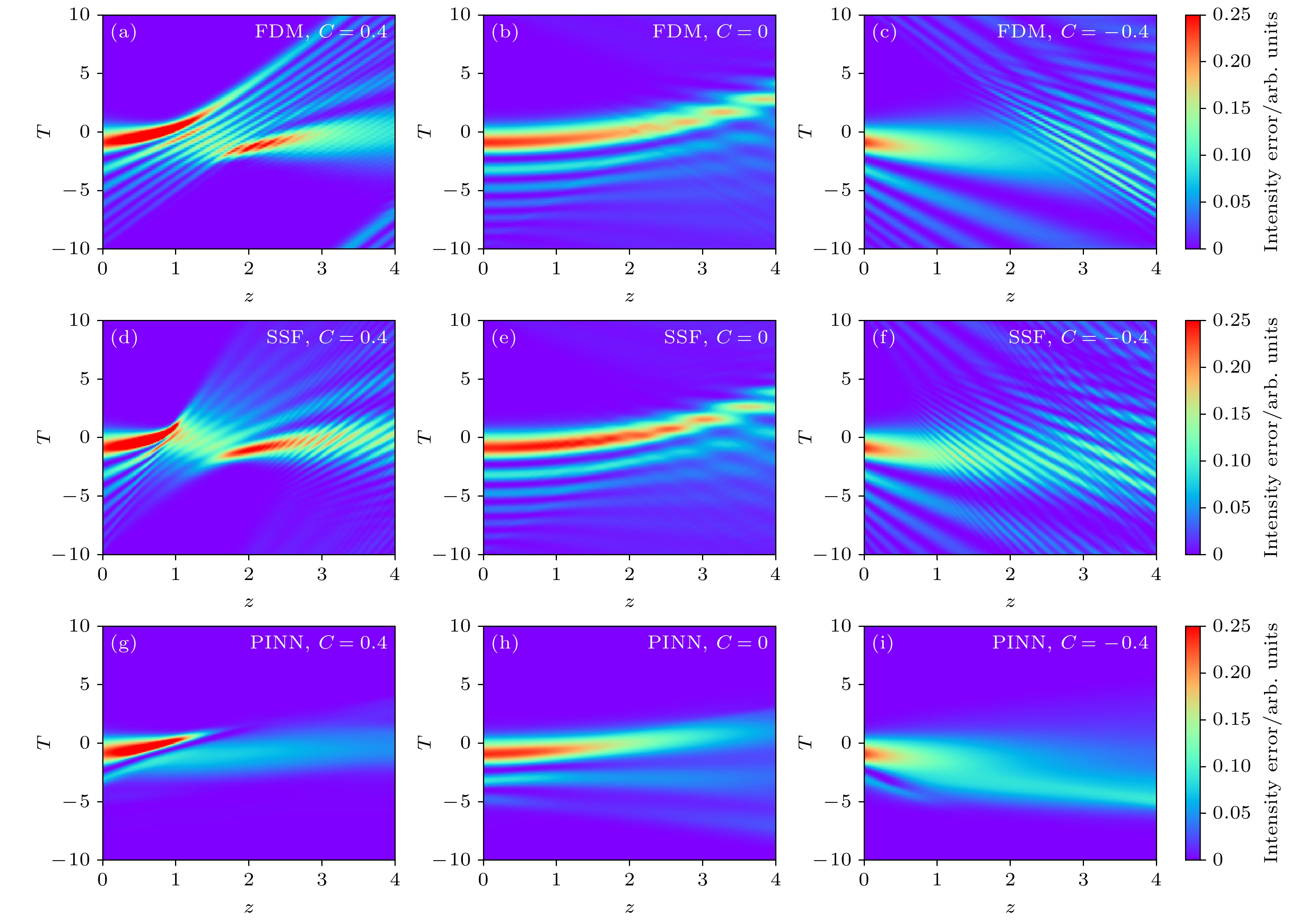
图 9 多种NLSE求解方法对比不同啁啾艾里脉冲在光纤传输中演化 (a)—(c)分别为对应于FDM, 在C = 0.4, 0, –0.4时的脉冲演化; (d)—(f)分别为对应于SSF, 在C = 0.4, 0, –0.4时的脉冲演化; (g)—(i)分别为对应于PINN, 在C = 0.4, 0, –0.4时的脉冲演化
Fig. 9. Comparison of Airy pulses’ evolution with different chirps by various NLSE solving methods in fiber transmission: (a)–(c) The pulse evolution corresponding to FDM with C values of 0.4, 0, –0.4; (d)–(f) the pulse evolution corresponding to SSF with C values of 0.4, 0, –0.4; (g)–(i) the pulse evolution corresponding to PINN with C values of 0.4, 0, –0.4.
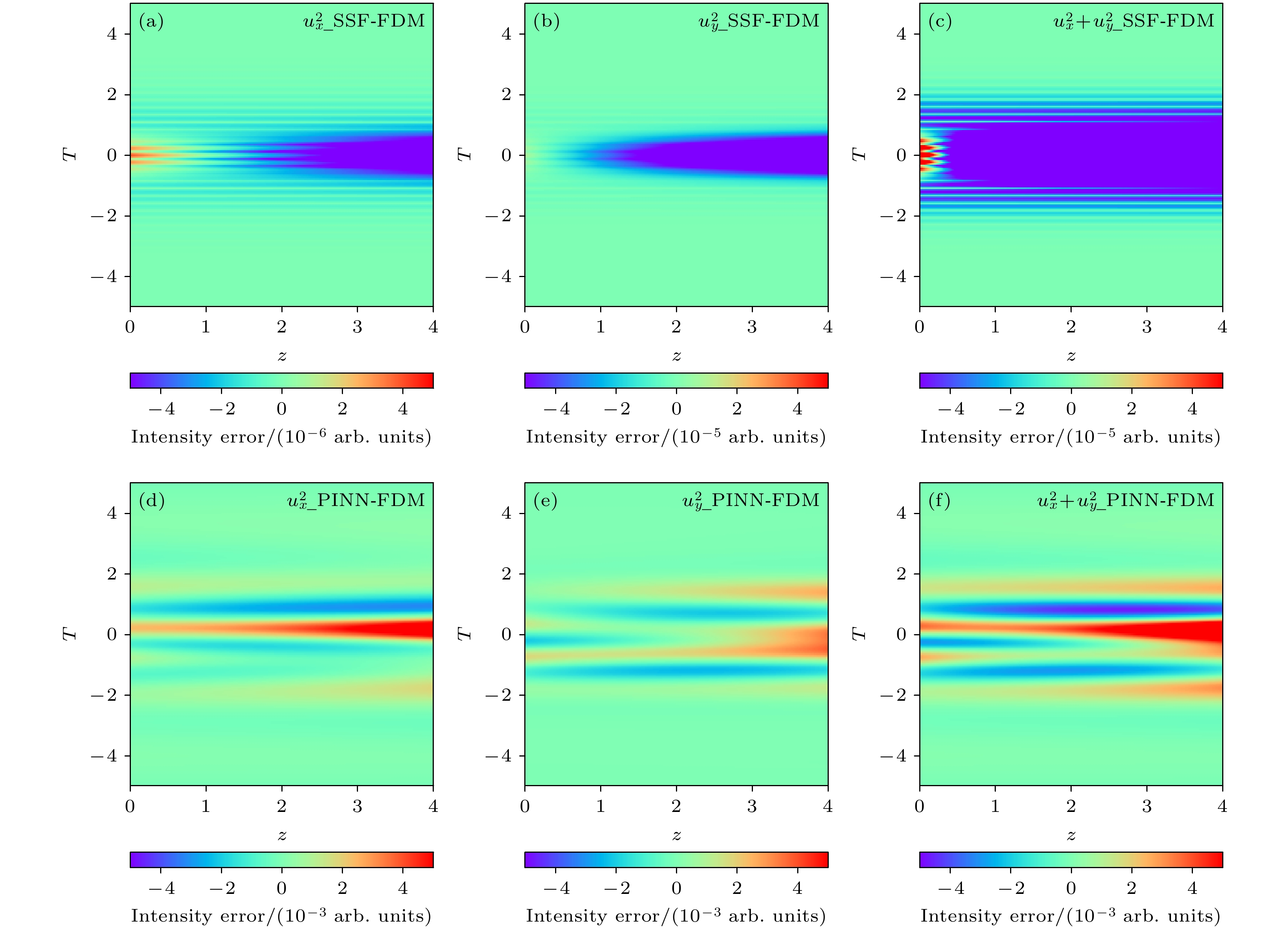
图 10 SSF, FDM和PINN求解VNLSE对应的脉冲演化过程的交叉对比图 (a) SSF与FDM关于$u_x^2$ 的交叉对比图; (b) SSF与FDM关于$u_y^2$的交叉对比图; (c) SSF与FDM关于$ u_x^2{+}u_y^2 $的交叉对比图; (d) PINN与FDM关于$u_x^2$的交叉对比图; (e) PINN与FDM关于$u_y^2$的交叉对比图; (f) PINN与FDM关于$ u_x^2{+}u_y^2 $的交叉对比图
Fig. 10. Comparison of the pulse evolution process corresponding to VNLSE solved by SSF, FDM and PINN: (a) SSF and FDM with respect to $u_x^2$; (b) SSF and FDM with respect to $u_y^2$; (c) SSF and FDM with respect to $ u_x^2{+}u_y^2 $; (d) PINN and FDM with respect to $u_x^2$; (e) PINN and FDM with respect to $u_y^2$; (f) PINN and FDM with respect to $ u_x^2{+}u_y^2 $.
表 1 集成学习和单一方法的误差表
Table 1. Error table of Ensemble Learning and single method.
MAE MSE RMSE MAPE/% FDM 4.014×10–4 4.877×10–7 6.983×10–4 13.159 SSF 3.396×10–4 3.112×10–7 5.579×10–4 8.979 PINN 4.173×10–4 4.744×10–7 6.887×10–4 11.540 SSF+FDM 2.625×10–4 1.466×10–7 3.829×10–4 10.933 PINN+FDM 2.865×10–4 2.316×10–7 4.652×10–4 10.048 PINN+SSF 2.793×10–4 1.753×10–7 4.188×10–4 12.237 PINN+FDM+SSF 2.190×10–4 0.978×10–7 3.127×10–4 11.004 
下载: 导出CSV
-
[1] 阿戈沃 G P著 (贾东方, 余震虹 译) 2010 非线性光纤光学原理及应用 (北京: 电子工业出版社) 第18—109页
Agrawal G P (translated by Jia D F, Yu Z H) 2010 Principles and Applications of Nonlinear Fibre Optics (Beijing: Electronic Industry Press) pp18–109
[2] Ngo N Q 2018 Ultra-fast Fiber Lasers: Principles and Applications with MATLAB® Models (Boca Raton: CRC Press) pp139–157
[3] Chang Q S, Jia E H, Sun W 1999 J. Comput. Phys. 148 397
Google Scholar
[4] Wang H Q 2005 Appl. Math. Comput. 170 17
Google Scholar
[5] 赵磊, 隋展, 朱启华, 张颖, 左言磊 2009 58 3977
Google Scholar
Zhao L, Sui Z, Zhu Q H, Zhang Y, Zuo Y L 2009 Acta Phys. Sin. 58 3977
Google Scholar
[6] Xie S S, Li G X, Yi S 2009 Comput. Meth. Appl. Mech. Eng. 198 1052
Google Scholar
[7] Wu L 2012 Numer. Meth. Partial Differ. Eq. 28 63
Google Scholar
[8] Caplan R M 2013 Appl. Numer. Math. 71 24
Google Scholar
[9] 崔少燕, 吕欣欣, 辛杰 2016 65 040201
Google Scholar
Cui S Y, Lv X X, Xin J 2016 Acta Phys. Sin. 65 040201
Google Scholar
[10] Feng X B, Li B Y, Ma S 2021 SIAM J. Numer. Anal. 59 1566
Google Scholar
[11] Ibarra-Villalón H E, Pottiez O, Gómez-Vieyra A, Lauterio-Cruz J P, Bracamontes- Rodriguez Y E 2023 Phys. Scr. 98 065514
Google Scholar
[12] Zhang L F, Liu K, Zhong H Z, Zhang J G, Li Y, Fan D Y 2015 Opt. Express 23 2566
Google Scholar
[13] Yu Y, Zhang Y T, Song X X, Zhang H T, Cao M X, Che Y L, Zhang H, Yao J Q 2017 IEEE Photonics J. 9 7904107
Google Scholar
[14] Xin W, Wang Y, Xin Z G, Li L 2021 Opt. Commun. 489 126889
Google Scholar
[15] 罗民, 张泽贤, 陈乃妙, 刘萌, 罗爱平, 徐文成, 罗智超 2023 72 204203
Google Scholar
Luo M, Zhang Y Z, Chen N M, Liu M, Luo A P, Xu W C, Luo Z C 2023 Acta Phys. Sin. 72 204203
Google Scholar
[16] Lawal Z K, Yassin H, Lai D T, Che-Idris A 2022 Big Data Cogn. Comput. 6 140
Google Scholar
[17] Karniadakis G E, Kevrekidis I G, Lu L, Perdikaris P, Wang S, Yang L 2021 Nat. Rev. Phys. 3 422
Google Scholar
[18] 李野, 陈松灿 2022 计算机科学 49 254
Google Scholar
Li Y, Chen S C 2022 Comput. Sci. 49 254
Google Scholar
[19] Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686
Google Scholar
[20] Pu J C, Peng W Q, Chen Y 2021 Wave Motion. 107 102823
Google Scholar
[21] Pu J C, Li J, Chen Y 2021 Nonlinear Dyn. 105 1723
Google Scholar
[22] Wang L, Yan Z Y 2021 Phys. Lett. A 404 127408
Google Scholar
[23] Zang Y B, Yu Z M, Xu K, Chen M H, Yang S G, Chen H W 2021 J. Lightwave Technol. 40 404
Google Scholar
[24] Jiang X T, Wang D S, Chen X, Zhang M 2022 J. Lightwave Technol. 40 21
Google Scholar
[25] Jiang X T, Wang D S, Fan Q R, Zhang M, Lu C, Lau A P 2022 Laser Photonics Rev. 16 2100483
Google Scholar
[26] Fang Y, Bo W B, Wang R R, Wang W W, Chao Q D 2022 Chaos Soliton. Fract. 165 112908
Google Scholar
[27] 田十方, 李彪 2023 72 100202
Google Scholar
Tian S F, Li B 2023 Acta Phys. Sin. 72 100202
Google Scholar
[28] 罗霄, 张民, 蒋啸天, 宋裕琛, 张希萌, 王丹石 2023 红外与激光工程 52 12
Google Scholar
Luo X, Zhang M, Jiang X T, Song X M, Zhang X M, Wang D S 2023 Infrared Laser Eng. 52 12
Google Scholar
[29] Thulasidharan K, Sinthuja N, Priya N V, Senthilvelan M 2024 Commun. Theor. Phys. 76 115801
Google Scholar
[30] Psaros A F, Kawaguchi K, Karniadakis G E 2022 J. Comput. Phys. 458 111121
Google Scholar
[31] Uduagbomen J, Leeson M S, Liu Z, Lakshminarayana S, Xu T H 2024 Appl. Opt. 63 3794
Google Scholar
[32] Cuomo S, Di Cola V S, Giampaolo F, Rozza G, Raissi M, Piccialli F 2022 J. Sci. Comput. 92 88
Google Scholar
[33] Lu L, Meng X H, Mao Z P, Karniadakis G E 2019 SIAM Rev. 63 208
Google Scholar
[34] Yu J, Lu L, Meng X H, Karniadakis G E 2022 Comput. Methods Appl. Mech. Eng. 393 114823
Google Scholar
[35] Wang T M, Cai L J, Xia C J, Song H, Li L B, Bai G X, Fu N Q, Xian L D, Yang R, Mu H R, Zhang G Y, Lin S H 2024 Adv. Sci. 11 2406476
Google Scholar
[36] Gong K W, Li L B, Yu W Z 2023 Mater. Des. 228 111848
Google Scholar
[37] Ding B B, Li L B, Gong K W 2023 Appl. Surf. Sci. 22 156944
Google Scholar
[38] Mao D, He Z W, Zhang Y S, Du Y Q, Zeng C, Yun L, Luo Z C, Li T J, Sun Z P, Zhao J L 2022 Light Sci. Appl. 11 25
Google Scholar
[39] Mao D, Wang H, Zhang H, Zeng C, Du Y Q, He Z W, Sun Z P, Zhao J L 2021 Nat. Commun. 12 6712
Google Scholar
[40] Mao D, Gao Q, Li J Y, He Z W, Du Y Q, Zeng C, Sun Z P, Zhao J L 2022 Phys. Rev. Appl. 18 044044
Google Scholar
[41] Rao C P, Ren P, Wang Q, Buyukozturk O, Sun H, Liu Y 2023 Nat. Mach. Intell. 5 765
Google Scholar
[42] Cao R H, Su J, Feng J Q, Guo Q 2024 Electron. Res. Arch. 32 6641
Google Scholar
[43] Ismail M S, Alamri S Z 2004 Int. J. Comput. Math. 81 333
Google Scholar
[44] Wang T 2011 J. Comput. Appl. Math. 235 4237
Google Scholar
[45] Wu G Z, Fang Y, Wang Y Y, Wu G C, Dai C Q 2021 Chaos Solitons Fractals 152 111393
Google Scholar
下载:
计量
- 文章访问数: 3736
- PDF下载量: 184
- 被引次数: 0
