-
钨杂质聚芯控制对于托卡马克的稳态运行十分重要, 本文主要采用杂质输运程序STRAHL模拟研究了新经典输运对钨杂质在芯部聚集的影响. 针对HL-3装置未来采用钨偏滤器、在氩气注入放电情况开展研究, 其中边缘和芯部背景等离子体参数分别由SOLPS-ITER及OMFIT模拟获得. 边界区域的钨杂质输运使用IMPEDGE程序进行模拟, 并同STRAHL的结果进行对比, 以确保芯边杂质分布的一致性和模拟结果的准确性, 从而得到钨杂质从边界区域至芯部的完整分布. 在此基础上, 分别模拟了有无新经典对流情况下钨杂质的输运. 模拟结果表明, 无新经典对流时, 湍流输运主导杂质输运, 其方向指向内, 会导致杂质在芯部聚集. 加入新经典对流后, 其方向指向外, 其在一定程度上抵消了向内的湍流对流, 从而显著降低芯部钨杂质密度. 其中区域$ \rho =0.72—0.90 $的新经典对流对芯部杂质密度下降起到更为重要的作用. 进一步分析新经典对流各分量, 研究表明Pfirsche-Schlüter (PS)分量主导新经典对流项, 其主要是由离子温度梯度项驱动. 因此, 实验上可以通过加热等方式, 增强离子温度梯度, 抑制杂质聚芯.Controlling of tungsten (W) impurity core accumulation is of great significance for the steady-state operation of tokamaks. This work mainly investigates the effect of neoclassical transport on the core accumulation of W impurities by using STRAHL code. The study focuses on the HL-3 device, which will use tungsten divertor and conduct research under argon gas injection discharge conditions. In the simulation, the edge and core background plasma parameters are obtained by SOLPS-ITER and OMFIT simulations, respectively. The distribution of tungsten impurities in the boundary region is simulated using the IMPEDGE code. The edge anomalous transport coefficient in STRAHL is adjusted accordingly, and the simulation results are compared with those from the IMPEDGE to ensure consistency in impurity distribution between the core and edge. In the core region, a numerical scan is performed to adjust the simulation results so that the energy radiation matches the setting values, thereby determining the specific turbulence convection velocity. By setting the coefficients for both the core region and the boundary region, a complete distribution of W impurities from boundary to the core is obtained. To account for the neoclassical transport effects, the neoclassical transport coefficients are calculated using the subroutine NEOART and applied to the impurity transport simulation, and the simulation region is set from $ \rho =0 $ to 0.9. On this basis, the transport of W impurities with and without neoclassical convection is simulated. The simulation results show that without neoclassical convection, anomalous transport dominates the impurity transport, which is inward and enhances impurity accumulation in the core, and the core impurity density reaches $ 1.1\times {10}^{16}\;{{\mathrm{m}}}^{-3} $. After introducing neoclassical convection which is outward, it can offset the inward anomalous convection and significantly reduces the W impurity density in the core, thereby significantly reducing the core tungsten impurity density to $ 4.0\times {10}^{15}\;{{\mathrm{m}}}^{-3} $. In addition, the neoclassical convection in the region of $ \rho$ = 0.72–0.90 plays a more important role in reducing the core impurity density. Further analysis of the components of neoclassical convection shows that the Pfirsche-Schlüter (PS) component dominates the neoclassical convection term, which is mainly driven by the ion temperature gradient term. Therefore, experimentally, plasma heating can be used to enhance the temperature gradient and suppress impurity core accumulation.
-
Keywords:
- magnetic confinement fusion /
- neoclassical transport /
- core tungsten impurity accumulation
[1] Neu R, Dux R, Geier A, Kallenbach A, Pugno R, Rohde V, Bolshukhin D, Fuchs J C, Gehre O, Gruber O, Hobirk J, Kaufmann M, Krieger K, Laux M, Maggi C, Murmann H, Neuhauser J, Ryter F, Sips A C C, Stäbler A, Stober J, Suttrop W, Zohm H 2002 Plasma Phys. Control. Fusion 44 811
Google Scholar
[2] Sang C F, Zhou Q R, Xu G S, Wang L, Wang Y L, Zhao X L, Zhang C, Ding R, Jia G Z, Yao D M, Liu X J, Si H, Wang D Z, the EAST Team 2021 Nucl. Fusion 61 066004
Google Scholar
[3] Liu B, Dai S Y, Yang X D, Chan V S, Ding R, Zhang H M, Feng Y, Wang D Z 2022 Nucl. Fusion 62 126040
Google Scholar
[4] Pitts R A, Bonnin X, Escourbiac F, Frerichs H, Gunn J P, Hirai T, Kukushkin A S, Kaveeva E, Miller M A, Moulton D, Rozhansky V, Senichenkov I, Sytova E, Schmitz O, Stangeby P C, De Temmerman G, Veselova I, Wiesen S 2019 Nucl. Mater. Energy 20 100696
Google Scholar
[5] Gruber O, Sips A C C, Dux R, Eich T, Fuchs J C, Herrmann A, Kallenbach A, Maggi C F, Neu R, Pütterich T, Schweinzer J, Stober J 2009 Nucl. Fusion 49 115014
Google Scholar
[6] Sun Z C, Lian Z W, Qiao W N, Yu J G, Han W J, Fu Q W, Zhu K G 2017 Chin. Phys. Lett. 34 030205
Google Scholar
[7] 张启凡, 乐文成, 张羽昊, 葛忠昕, 邝志强, 萧声扬, 王璐 2024 73 185201
Google Scholar
Zhang Q F, Le W C, Zhang Y H, Ge Z X, Kuang Z Q, Xiao S Y, Wang L 2024 Acta Phys. Sin. 73 185201
Google Scholar
[8] Angioni C 2021 Plasma Phys. Control. Fusion 63 073001
Google Scholar
[9] Guirlet R, Giroud C, Parisot T, Puiatti M E, Bourdelle C, Carraro L, Dubuit N, Garbet X, Thomas P R 2006 Plasma Phys. Control. Fusion 48 B63
Google Scholar
[10] Donnel P 2018 Ph. D. Dissertation (Aix-Marseille: Aix Marseille Université
[11] Shi S Y, Chen J L, Bourdelle C, Jian X, Odstrčil T, Garofalo A M, Cheng Y X, Chao Y, Zhang L, Duan Y M, Wu M Q, Ding F, Li Y Y, Huang J, Qian J P, Gao X, Wan Y X 2022 Nucl. Fusion 62 066031
Google Scholar
[12] Shi S, Chen J, Jian X, Odstrčil T, Clarrisse B, Wu M, Wu M, Duan Y, Chao Y, Zhang L, Cheng Y, Qian J, Garofalo A M, Gong X, Gao X, Wan Y 2022 Nucl. Fusion 62 066040
Google Scholar
[13] Pütterich T, Dux R, Neu R, Bernert M, Beurskens M N A, Bobkov V, Brezinsek S, Challis C, Coenen J W, Coffey I, Czarnecka A, Giroud C, Jacquet P, Joffrin E, Kallenbach A, Lehnen M, Lerche E, de la Luna E, Marsen S, Matthews G, Mayoral M L, McDermott R M, Meigs A, Mlynar J, Sertoli M, van Rooij G 2013 Plasma Phys. Control. Fusion 55 124036
Google Scholar
[14] Lee H, Lee H, Han Y S, Song J, Belli E A, Choe W, Kang J, Lee J, Candy J, Lee J 2022 Phys. Plasmas 29 022504
Google Scholar
[15] 赵伟宽, 张凌, 程云鑫, 周呈熙, 张文敏, 段艳敏, 胡爱兰, 王守信, 张丰玲, 李政伟, 曹一鸣, 刘海庆 2024 73 035201
Google Scholar
Zhao W K, Zhang L, Cheng Y X, Zhou C X, Zhang W M, Duan Y M, Hu A L, Wang S X, Zhang F L, Li Z W, Cao Y M, Liu H Q 2024 Acta Phys. Sin. 73 035201
Google Scholar
[16] Mochinaga S, Kasuya N, Fukuyama A, Yagi M 2024 Nucl. Fusion 64 066002
Google Scholar
[17] Lim K, Garbet X, Sarazin Y, Gravier E, Lesur M, Lo-Cascio G, Rouyer T 2023 Phys. Plasmas 30 082501
Google Scholar
[18] Zheng G Y, Cai L Z, Duan X R, Xu X Q, Ryutov D D, Cai L J, Liu X, Li J X, Pan Y D 2016 Nucl. Fusion 56 126013
Google Scholar
[19] Cao C Z, Huang X M, Hu Y, Xie Y F, Zhou J, Qiao T, Gao J M, Cai L Z, Cao Z, HL-2A and HL-3 team 2025 Nucl. Mater. Energy 42 101852
Google Scholar
[20] Han J Y, He Y X, Zhao D Y, Cai L Z, Wang Y Q, Qian W, Huang W Y, Lu Y, Cai L J, Zhong W L 2025 Nucl. Mater. Energy 42 101861
Google Scholar
[21] Zhang X L, He Z Y H, Cheng Z F, Yan W, Dong Y B, Liu Y, Deng W, Fu B Z, Shi Z B, Zhang Y P, Shi Y J 2024 Fusion Eng. Des. 208 114674
Google Scholar
[22] Zhou Q R, Zhang Y J, Sang C F, Li J X, Zheng G Y, Wang Y L, Wu Y H, Wang D Z 2024 Plasma Sci. Technol. 26 104003
Google Scholar
[23] Zhang Y J, Sang C F, Li J X, Zheng G Y, Senichenkov I Y, Rozhansky V A, Zhang C, Wang Y L, Zhao X L, Wang D Z 2022 Nucl. Fusion 62 106006
Google Scholar
[24] Dux R 2006 STRAHL User Manual Report
[25] Wu Y H, Zhou Q R, Sang C F, Zhang Y J, Wang Y L, Wang D Z 2022 Nucl. Mater. Energy 33 101297
Google Scholar
[26] Zhou Y, Zheng G Y, Du H L, Li J X, Xue L 2022 Fusion Eng. Des. 182 113222
Google Scholar
[27] Jirakova K, Kovanda O, Adamek J, Komm M, Seidl J 2019 J. Instrum. 14 C11020
Google Scholar
[28] Wang J F, Wu B, Wang J, Hu C D 2013 J. Fusion Energy 33 20
Google Scholar
[29] Candy J, Holland C, Waltz R E, Fahey M R, Belli E 2009 Phys. Plasmas 16 060704
Google Scholar
[30] Logan N C, Grierson B A, Haskey S R, Smith S P, Meneghini O, Eldon D 2018 Fusion Sci. Technol. 74 125
Google Scholar
[31] Dux R, Loarte A, Angioni C, Coster D, Fable E, Kallenbach A 2017 Nucl. Mater. Energy 12 28
Google Scholar
[32] Dubuit N, Garbet X, Parisot T, Guirlet R, Bourdelle C 2007 Phys. Plasmas 14 042301
Google Scholar
[33] Dux R 2004 Ph. D. Dissertation (Garching: Max Planck Institut für Plasmaphysik
[34] Wang Y L, Sang C F, Zhao X L, Wu Y H, Zhou Q R, Zhang Y J, Wang D Z 2023 Nucl. Fusion 63 096024
Google Scholar
[35] 杜海龙, 桑超峰, 王亮, 孙继忠, 刘少承, 汪惠乾, 张凌, 郭后扬, 王德真 2013 62 245206
Google Scholar
Du H L, Sang C F, Wang L, Sun J Z, Liu S C, Wang H Q, Zhang L, Guo H Y, Wang D Z 2013 Acta Phys. Sin. 62 245206
Google Scholar
[36] Wang Y L, Sang C F, Zhang C, Zhao X L, Zhang Y J, Jia G Z, Senichenkov I Y, Wang L, Zhou Q R, Wang D Z 2021 Plasma Phys. Control. Fusion 63 085002
Google Scholar
[37] Sang C F, Ding R, Bonnin X, Wang L, Wang D Z, EAST Team 2018 Phys. Plasmas 25 072511
Google Scholar
[38] Zhao X L, Sang C F, Zhou Q R, Zhang C, Zhang Y J, Ding R, Ding F, Wang D Z 2020 Plasma Phys. Control. Fusion 62 055015
Google Scholar
[39] Zhou Q R, Sang C F, Xu G L, Ding R, Zhao X L, Wang Y L, Wang D Z 2020 Nucl. Mater. Energy 25 100849
Google Scholar
[40] Shi S Y, Chen J L, Bourdelle C, Jian X, Odstrčil T, Garofalo A M, Cheng Y X, Chao Y, Zhang L, Duan Y M, Wu M F, Ding F, Qian J P, Gao X 2022 Nucl. Fusion 62 066032
Google Scholar
[41] Shi S Y, Jian X, Chan V S, Gao X, Liu X J, Shi N, Chen J L, Liu L, Wu M Q, Zhu Y R, CFETR Physics Team 2018 Nucl. Fusion 58 126020
Google Scholar
[42] Wesson J 2011 Tokamaks (Oxford: Oxford University Press) pp153–161
-
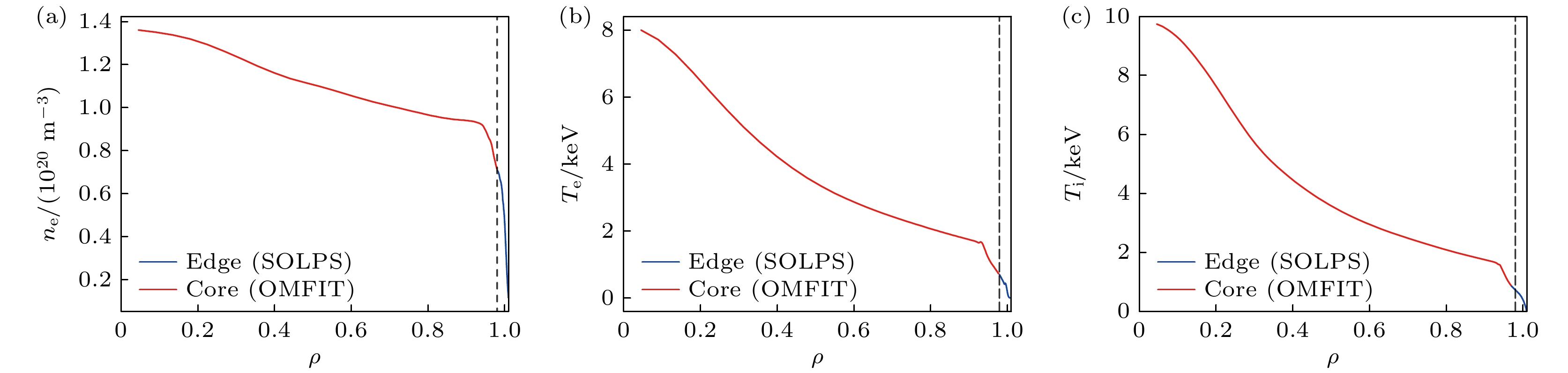
图 2 $ \rho $= 0—1.01区域参数的径向剖面 (a)电子密度ne; (b)电子温度 Te; 和(c)离子温度Ti; 其中红线代表芯部$ \rho $= 0—0.98区域参数(OMFIT提供), 蓝线代表边缘$ \rho $= 0.98—1.01区域参数(SOLPS-ITER模拟), 虚线代表$ \rho $= 0.98位置
Fig. 2. Radial profiles in the region $ \rho $= 0–1.01: (a) Electron density ne; (b) electron temperature Te; (c) ion temperature Ti. The red line represents the core $ \rho $= 0–0.98 region parameter (provided by OMFIT), the blue line represents the edge $ \rho $= 0.98–1.01 region parameters (provided by SOLPS-ITER), and the dashed line represents the $ \rho $= 0.98 location.
图 3 (a) $ \rho $= 0.98—1.01区域的杂质分布, 其中蓝线为IMPEDGE模拟分布, 蓝点为STRAHL模拟分布; (b) $ \rho $= 0.98—1.01区域湍流扩散系数$ {D}^{{\mathrm{A}}{\mathrm{N}}{\mathrm{O}}} $与对流速度$ {v}^{{\mathrm{A}}{\mathrm{N}}{\mathrm{O}}} $分布; (c) $ \rho = $0—0.98区域湍流扩散系数$ {D}^{{\mathrm{A}}{\mathrm{N}}{\mathrm{O}}} $与对流速度$ {v}^{{\mathrm{A}}{\mathrm{N}}{\mathrm{O}}} $分布
Fig. 3. (a) Impurity distribution in the region $ \rho $= 0.98–1.01, the blue line represents the IMPEDGE simulation distribution, and the blue dots represent the STRAHL simulation distribution; (b) anomalous diffusion coefficient $ {D}^{{\mathrm{A}}{\mathrm{N}}{\mathrm{O}}} $and convective velocity $ {v}^{{\mathrm{A}}{\mathrm{N}}{\mathrm{O}}} $distributions in the region $ \rho $= 0.98–1.01; (c) anomalous diffusion coefficient $ {D}^{{\mathrm{A}}{\mathrm{N}}{\mathrm{O}}} $and convective velocity $ {v}^{{\mathrm{A}}{\mathrm{N}}{\mathrm{O}}} $ distributions in the region in the region $ \rho = $0–0.98.
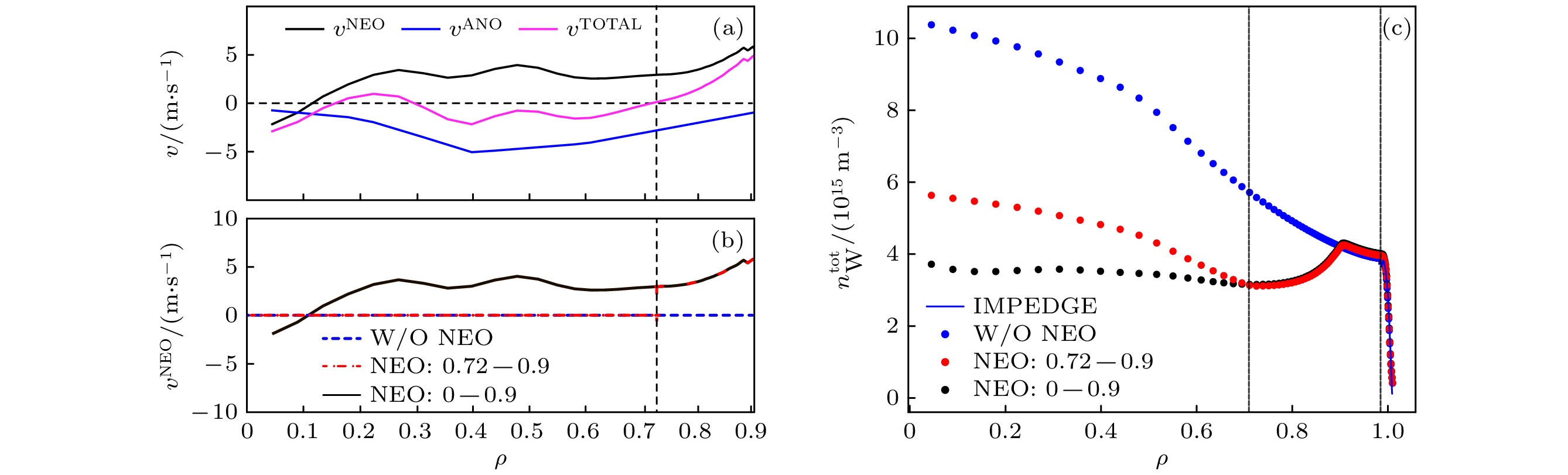
图 4 区域$ \rho =0—0.9 $ (a) $ {v}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $, $ {v}^{{\mathrm{A}}{\mathrm{N}}{\mathrm{O}}} $和$ {v}^{{\mathrm{T}}{\mathrm{O}}{\mathrm{T}}{\mathrm{A}}{\mathrm{L}}} $径向分布; (b) 3种情况下$ {v}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $分布设置; (c) 区域$ \rho =0—1.01 $三种情况下模拟得到的钨杂质密度$ {n}_{{\mathrm{W}}}^{{\mathrm{t}}{\mathrm{o}}{\mathrm{t}}} $径向分布, 其中杂质边缘分布均与IMPEDGE一致, 虚线分别表示$ \rho $= 0.72和$ \rho $= 0.98所在位置
Fig. 4. (a) The radial distributions of $ {v}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $, $ {v}^{{\mathrm{A}}{\mathrm{N}}{\mathrm{O}}} $, and $ {v}^{{\mathrm{T}}{\mathrm{O}}{\mathrm{T}}{\mathrm{A}}{\mathrm{L}}} $; (b) the setup of $ {v}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $ distribution for three different cases in the region $ \rho$ = 0–0.9; (c) radial distribution of tungsten impurity density $ {n}_{{\mathrm{W}}}^{{\mathrm{t}}{\mathrm{o}}{\mathrm{t}}} $ of different cases in the region $ \rho$ = 0–1.01, the $ {n}_{{\mathrm{W}}}^{{\mathrm{t}}{\mathrm{o}}{\mathrm{t}}} $ distributions in the edge region are consistent with those from IMPEDGE. The dashed lines represent the $ \rho =0.72 $ and $ \rho =0.98 $ location.
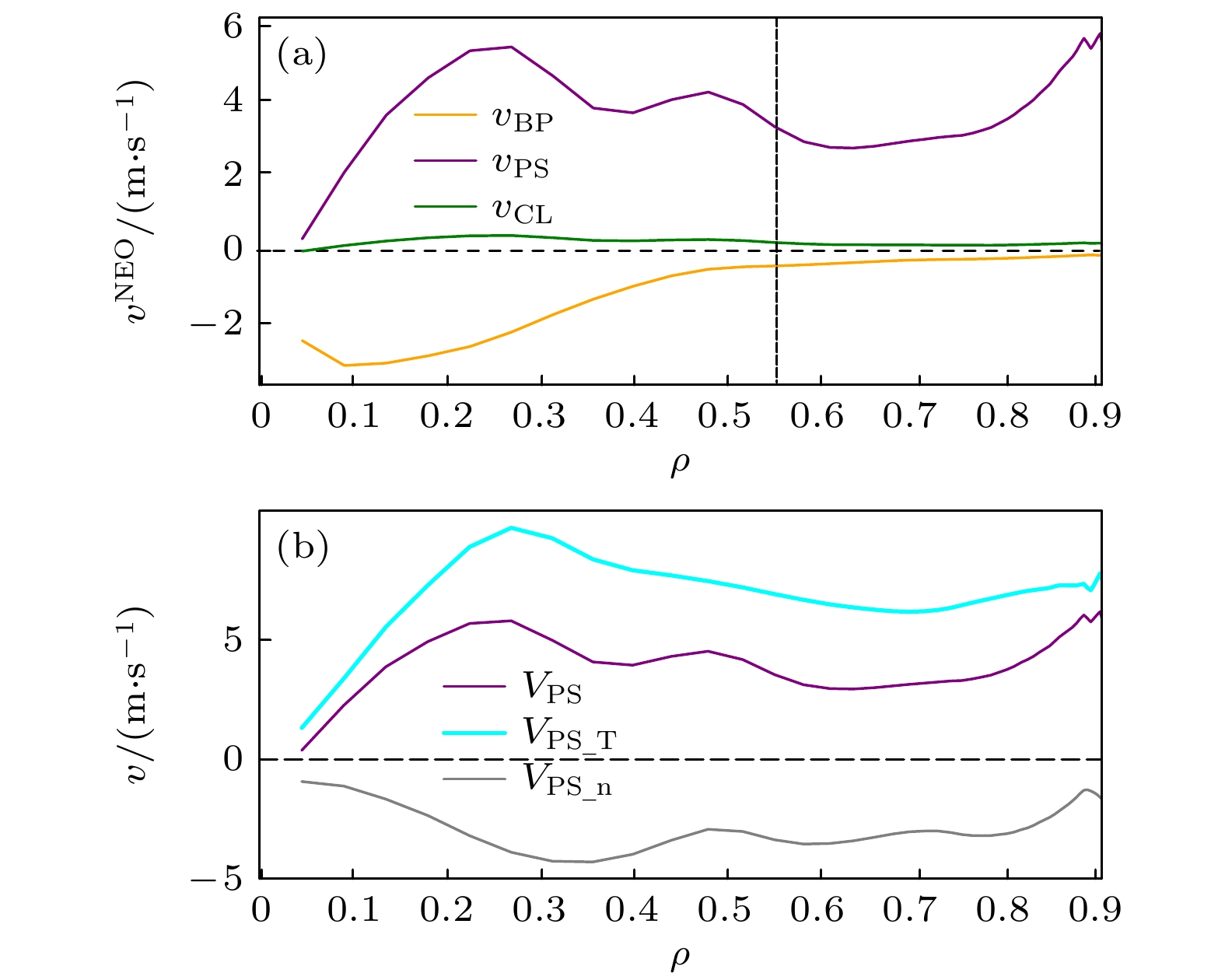
图 5 区域$ \rho =0—0.9 $ (a)新经典对流速度的3个分量; (b)新经典对流PS分量$ {v}_{{\mathrm{P}}{\mathrm{S}}}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $及离子温度梯度项$ {v}_{{\mathrm{P}}{\mathrm{S}}\_{\mathrm{T}}}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $和密度梯度项$ {v}_{{\mathrm{P}}{\mathrm{S}}\_{\mathrm{n}}}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $, 虚线位置为$ \rho =0.55 $
Fig. 5. (a) Three components of the neoclassical convective velocity; (b) the neoclassical convective PS component $ {v}_{{\mathrm{P}}{\mathrm{S}}}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $ along with its temperature gradient term $ {v}_{{\mathrm{P}}{\mathrm{S}}\_{\mathrm{T}}}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $ and density gradient term $ {v}_{{\mathrm{P}}{\mathrm{S}}\_{\mathrm{n}}}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $ in region $ \rho =0$–0.9, the dashed line represents the $ \rho =0.55 $ location.
图 6 区域$ \rho =0—0.9 $杂质碰撞率$ {\nu }_{{\mathrm{I}}}^{{\mathrm{*}}} $分布, 虚线位置为$ \rho =0.55 $
Fig. 6. Impurity collision rate $ {\nu }_{{\mathrm{I}}}^{{\mathrm{*}}} $ distribution in the region $ \rho$ = 0–0.9 , the dashed line represents the $ \rho =0.55 $ location.
表 1 不同$ {v}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $使用区域情况下的$ \rho =0 $和$ \rho =0.72 $处钨密度, $ \rho =0 $处钨浓度, $ \rho =0 $处钨杂质引起的总辐射损失密度
Table 1. In different $ {v}^{{\mathrm{N}}{\mathrm{E}}{\mathrm{O}}} $ applied region cases, the tungsten density at $ \rho =0 $ and $ \rho =0.72 $, the tungsten concentration at $ \rho =0 $ and total power radiation loss density by tungsten at $ \rho =0 $.
使用区域 W/O NEO With NEO
$ \rho $= 0.72—0.90With NEO
$ \rho $= 0—0.9$ {n}_{{\mathrm{w}}}^{\rho =0.72} $(1015 m–3) $ 6.00 $ $ 3.80 $ $ 3.80 $ $ {n}_{{\mathrm{w}}}^{\rho =0} $(1016 m–3) $ 1.10 $ $ 0.58 $ $ 0.40 $ $ {C}_{{\mathrm{w}}}^{\rho =0} $(10–5) 7.70 4.20 2.50 $ {P}_{{\mathrm{r}}{\mathrm{a}}{\mathrm{d}}}^{\rho =0} $(MW·m–3) 0.26 0.15 0.11 
下载: 导出CSV
-
[1] Neu R, Dux R, Geier A, Kallenbach A, Pugno R, Rohde V, Bolshukhin D, Fuchs J C, Gehre O, Gruber O, Hobirk J, Kaufmann M, Krieger K, Laux M, Maggi C, Murmann H, Neuhauser J, Ryter F, Sips A C C, Stäbler A, Stober J, Suttrop W, Zohm H 2002 Plasma Phys. Control. Fusion 44 811
Google Scholar
[2] Sang C F, Zhou Q R, Xu G S, Wang L, Wang Y L, Zhao X L, Zhang C, Ding R, Jia G Z, Yao D M, Liu X J, Si H, Wang D Z, the EAST Team 2021 Nucl. Fusion 61 066004
Google Scholar
[3] Liu B, Dai S Y, Yang X D, Chan V S, Ding R, Zhang H M, Feng Y, Wang D Z 2022 Nucl. Fusion 62 126040
Google Scholar
[4] Pitts R A, Bonnin X, Escourbiac F, Frerichs H, Gunn J P, Hirai T, Kukushkin A S, Kaveeva E, Miller M A, Moulton D, Rozhansky V, Senichenkov I, Sytova E, Schmitz O, Stangeby P C, De Temmerman G, Veselova I, Wiesen S 2019 Nucl. Mater. Energy 20 100696
Google Scholar
[5] Gruber O, Sips A C C, Dux R, Eich T, Fuchs J C, Herrmann A, Kallenbach A, Maggi C F, Neu R, Pütterich T, Schweinzer J, Stober J 2009 Nucl. Fusion 49 115014
Google Scholar
[6] Sun Z C, Lian Z W, Qiao W N, Yu J G, Han W J, Fu Q W, Zhu K G 2017 Chin. Phys. Lett. 34 030205
Google Scholar
[7] 张启凡, 乐文成, 张羽昊, 葛忠昕, 邝志强, 萧声扬, 王璐 2024 73 185201
Google Scholar
Zhang Q F, Le W C, Zhang Y H, Ge Z X, Kuang Z Q, Xiao S Y, Wang L 2024 Acta Phys. Sin. 73 185201
Google Scholar
[8] Angioni C 2021 Plasma Phys. Control. Fusion 63 073001
Google Scholar
[9] Guirlet R, Giroud C, Parisot T, Puiatti M E, Bourdelle C, Carraro L, Dubuit N, Garbet X, Thomas P R 2006 Plasma Phys. Control. Fusion 48 B63
Google Scholar
[10] Donnel P 2018 Ph. D. Dissertation (Aix-Marseille: Aix Marseille Université
[11] Shi S Y, Chen J L, Bourdelle C, Jian X, Odstrčil T, Garofalo A M, Cheng Y X, Chao Y, Zhang L, Duan Y M, Wu M Q, Ding F, Li Y Y, Huang J, Qian J P, Gao X, Wan Y X 2022 Nucl. Fusion 62 066031
Google Scholar
[12] Shi S, Chen J, Jian X, Odstrčil T, Clarrisse B, Wu M, Wu M, Duan Y, Chao Y, Zhang L, Cheng Y, Qian J, Garofalo A M, Gong X, Gao X, Wan Y 2022 Nucl. Fusion 62 066040
Google Scholar
[13] Pütterich T, Dux R, Neu R, Bernert M, Beurskens M N A, Bobkov V, Brezinsek S, Challis C, Coenen J W, Coffey I, Czarnecka A, Giroud C, Jacquet P, Joffrin E, Kallenbach A, Lehnen M, Lerche E, de la Luna E, Marsen S, Matthews G, Mayoral M L, McDermott R M, Meigs A, Mlynar J, Sertoli M, van Rooij G 2013 Plasma Phys. Control. Fusion 55 124036
Google Scholar
[14] Lee H, Lee H, Han Y S, Song J, Belli E A, Choe W, Kang J, Lee J, Candy J, Lee J 2022 Phys. Plasmas 29 022504
Google Scholar
[15] 赵伟宽, 张凌, 程云鑫, 周呈熙, 张文敏, 段艳敏, 胡爱兰, 王守信, 张丰玲, 李政伟, 曹一鸣, 刘海庆 2024 73 035201
Google Scholar
Zhao W K, Zhang L, Cheng Y X, Zhou C X, Zhang W M, Duan Y M, Hu A L, Wang S X, Zhang F L, Li Z W, Cao Y M, Liu H Q 2024 Acta Phys. Sin. 73 035201
Google Scholar
[16] Mochinaga S, Kasuya N, Fukuyama A, Yagi M 2024 Nucl. Fusion 64 066002
Google Scholar
[17] Lim K, Garbet X, Sarazin Y, Gravier E, Lesur M, Lo-Cascio G, Rouyer T 2023 Phys. Plasmas 30 082501
Google Scholar
[18] Zheng G Y, Cai L Z, Duan X R, Xu X Q, Ryutov D D, Cai L J, Liu X, Li J X, Pan Y D 2016 Nucl. Fusion 56 126013
Google Scholar
[19] Cao C Z, Huang X M, Hu Y, Xie Y F, Zhou J, Qiao T, Gao J M, Cai L Z, Cao Z, HL-2A and HL-3 team 2025 Nucl. Mater. Energy 42 101852
Google Scholar
[20] Han J Y, He Y X, Zhao D Y, Cai L Z, Wang Y Q, Qian W, Huang W Y, Lu Y, Cai L J, Zhong W L 2025 Nucl. Mater. Energy 42 101861
Google Scholar
[21] Zhang X L, He Z Y H, Cheng Z F, Yan W, Dong Y B, Liu Y, Deng W, Fu B Z, Shi Z B, Zhang Y P, Shi Y J 2024 Fusion Eng. Des. 208 114674
Google Scholar
[22] Zhou Q R, Zhang Y J, Sang C F, Li J X, Zheng G Y, Wang Y L, Wu Y H, Wang D Z 2024 Plasma Sci. Technol. 26 104003
Google Scholar
[23] Zhang Y J, Sang C F, Li J X, Zheng G Y, Senichenkov I Y, Rozhansky V A, Zhang C, Wang Y L, Zhao X L, Wang D Z 2022 Nucl. Fusion 62 106006
Google Scholar
[24] Dux R 2006 STRAHL User Manual Report
[25] Wu Y H, Zhou Q R, Sang C F, Zhang Y J, Wang Y L, Wang D Z 2022 Nucl. Mater. Energy 33 101297
Google Scholar
[26] Zhou Y, Zheng G Y, Du H L, Li J X, Xue L 2022 Fusion Eng. Des. 182 113222
Google Scholar
[27] Jirakova K, Kovanda O, Adamek J, Komm M, Seidl J 2019 J. Instrum. 14 C11020
Google Scholar
[28] Wang J F, Wu B, Wang J, Hu C D 2013 J. Fusion Energy 33 20
Google Scholar
[29] Candy J, Holland C, Waltz R E, Fahey M R, Belli E 2009 Phys. Plasmas 16 060704
Google Scholar
[30] Logan N C, Grierson B A, Haskey S R, Smith S P, Meneghini O, Eldon D 2018 Fusion Sci. Technol. 74 125
Google Scholar
[31] Dux R, Loarte A, Angioni C, Coster D, Fable E, Kallenbach A 2017 Nucl. Mater. Energy 12 28
Google Scholar
[32] Dubuit N, Garbet X, Parisot T, Guirlet R, Bourdelle C 2007 Phys. Plasmas 14 042301
Google Scholar
[33] Dux R 2004 Ph. D. Dissertation (Garching: Max Planck Institut für Plasmaphysik
[34] Wang Y L, Sang C F, Zhao X L, Wu Y H, Zhou Q R, Zhang Y J, Wang D Z 2023 Nucl. Fusion 63 096024
Google Scholar
[35] 杜海龙, 桑超峰, 王亮, 孙继忠, 刘少承, 汪惠乾, 张凌, 郭后扬, 王德真 2013 62 245206
Google Scholar
Du H L, Sang C F, Wang L, Sun J Z, Liu S C, Wang H Q, Zhang L, Guo H Y, Wang D Z 2013 Acta Phys. Sin. 62 245206
Google Scholar
[36] Wang Y L, Sang C F, Zhang C, Zhao X L, Zhang Y J, Jia G Z, Senichenkov I Y, Wang L, Zhou Q R, Wang D Z 2021 Plasma Phys. Control. Fusion 63 085002
Google Scholar
[37] Sang C F, Ding R, Bonnin X, Wang L, Wang D Z, EAST Team 2018 Phys. Plasmas 25 072511
Google Scholar
[38] Zhao X L, Sang C F, Zhou Q R, Zhang C, Zhang Y J, Ding R, Ding F, Wang D Z 2020 Plasma Phys. Control. Fusion 62 055015
Google Scholar
[39] Zhou Q R, Sang C F, Xu G L, Ding R, Zhao X L, Wang Y L, Wang D Z 2020 Nucl. Mater. Energy 25 100849
Google Scholar
[40] Shi S Y, Chen J L, Bourdelle C, Jian X, Odstrčil T, Garofalo A M, Cheng Y X, Chao Y, Zhang L, Duan Y M, Wu M F, Ding F, Qian J P, Gao X 2022 Nucl. Fusion 62 066032
Google Scholar
[41] Shi S Y, Jian X, Chan V S, Gao X, Liu X J, Shi N, Chen J L, Liu L, Wu M Q, Zhu Y R, CFETR Physics Team 2018 Nucl. Fusion 58 126020
Google Scholar
[42] Wesson J 2011 Tokamaks (Oxford: Oxford University Press) pp153–161
下载:
计量
- 文章访问数: 365
- PDF下载量: 24
- 被引次数: 0
