周期驱动非互易Aubry-André模型中的多重分形态和迁移率边

王宇佳; 徐志浩

doi:10.7498/aps.74.20241633

摘要

研究了在非互易Aubry-André模型中由方波式周期驱动所诱导的多重分形态和迁移率边. 通过数值计算逆参与率、能谱的实复转变以及平均逆参与率的标度分析等, 发现在以高于临界频率的驱动下系统展现完全的局域相. 同时在Floquet谱的特定区域存在CAT态, 不同于厄米情况, 其波函数分布的两个峰值展现非等权叠加的特性, 这是由非互易物理所决定的. 而以低于临界频率的驱动下, Floquet谱中存在迁移率边和多重分形态. 该研究结果为周期驱动系统中局域化性质的研究提供了新的视角.

关键词:

Abstract

In this work, we investigate the delocalization-localization transition of Floquet eigenstates in a driven chain with an incommensurate Aubry-André (AA) on-site potential and a small non-reciprocal hopping term that is driven periodically in time. The driving protocol is chosen such that the Floquet Hamiltonian corresponds to a localized phase in the high-frequency limit and a delocalized phase in the low-frequency limit. By numerically calculating the inverse participation ratio and the fractal dimension $D_q$, we identify a clear delocalization-localization transition of the Floquet eigenstates at a critical frequency $\omega_{c}\approx0.318\pi$. This transition aligns with the real-to-complex spectrum transition of the Floquet Hamiltonian. For the driven frequency $\omega>\omega_{\mathrm{c}}$, the system resides in a localized phase, and we observe the emergence of CAT states—linear superposition of localized single particle states—in the Floquet spectrum. These states exhibit weight distributions concentrated around a few nearby sites of the chain, forming two peaks of unequal weight due to the non-reciprocal effect, distinguishing them from the Hermitic case. In contrast, for $\omega<\omega_{\mathrm{c}}$, we identify the presence of a mobility edge over a range of driving frequencies, separating localized states (above the edge) from multifractal and extended states (below the edge). Notably, multifractal states are observed in the Floquet eigenspectrum across a broad frequency range. Importantly, we highlight that the non-driven, non-reciprocal AA model does not support multifractal states nor a mobility edge in its spectrum. Thus, our findings reveal unique dynamical signatures that do not exist in the non-driven non-Hermitian scenario, providing a fresh perspective on the localization properties of periodically driven systems. Finally, we provide a possible circuit experiment scheme for the periodically driven non-reciprocal AA model. In the following work, we will extend our research to clean systems, such as Stark models, to explore the influence of periodic driving on their localization properties.

Keywords:

作者及机构信息

王宇佳¹,
徐志浩^1,2

1.
山西大学理论物理研究所, 光量子技术与器件全国重点实验室, 太原　030006

2.
山西大学, 极端光学协同创新中心, 太原　030006

通信作者: 徐志浩, xuzhihao@sxu.edu.cn

基金项目: 国家自然科学基金(批准号: 12375016)、山西省基础研究计划(批准号: 20210302123442)、北京凝聚态物理国家实验室(批准号: 2023BNLCMPKF001)和山西省“1331 工程”重点学科建设计划资助的课题.

Authors and contacts

WANG Yujia¹,
XU Zhihao^1,2

1.
State Key Laboratory of Quantum Optics Technologies and Devices, Institute of Theoretical Physics, Shanxi University, Taiyuan 030006, China

2.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: XU Zhihao, xuzhihao@sxu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 12375016), the Fundamental Research Program of Shanxi Province, China (Grant No. 20210302123442), the Open Research Fund of Beijing National Laboratory for Condensed Matter Physics, China (Grant No. 2023BNLCMPKF001), and the Fund for Shanxi “1331 Project” Key Subjects, China.

文章全文

参考文献

[1]	Anderson P W 1958 Phys. Rev. 109 1492 Google Scholar
[2]	Tang L Z, Zhang G Q, Zhang L F, Zhang D W 2021 Phys. Rev. A 103 033325 Google Scholar
[3]	Schulz M, Hooley C A, Moessner R, Pollmann F 2019 Phys. Rev. Lett. 122 040606 Google Scholar
[4]	Lin X S, Chen X M, Guo G C, Gong M 2023 Phys. Rev. B 108 174206 Google Scholar
[5]	Dai Q, Lu Z P, Xu Z H 2023 Phys. Rev. B 108 144207 Google Scholar
[6]	Liu H, Lu Z P, Xia X, Xu Z H 2024 New J. Phys. 26 093007 Google Scholar
[7]	Li H, Dong Z L, Longhi S, Liang Q, Xie D Z, Yan B 2022 Phys. Rev. Lett. 129 220403 Google Scholar
[8]	Ganeshan S, Pixley J H, Das Sarma S 2015 Phys. Rev. Lett. 114 146601 Google Scholar
[9]	Aditya S, Sengupta K, Sen D 2023 Phys. Rev. B 107 035402 Google Scholar
[10]	Qi R, Cao J P, Jiang X P 2023 Phys. Rev. B 107 224201 Google Scholar
[11]	Zuo Z W, Kang D W 2022 Phys. Rev. A 106 013305 Google Scholar
[12]	Xu Z H, Xia X, Chen S 2021 Phys. Rev. B 104 224204 Google Scholar
[13]	Wang Y C, Xia X, Zhang L, Yao H P, Chen S, You J G, Zhou Q, Liu X J 2020 Phys. Rev. Lett. 125 196604 Google Scholar
[14]	Tang Q Y, He Y 2024 Phys. Rev. B 109 224204 Google Scholar
[15]	Zhou L W 2021 Phys. Rev. Res. 3 033184 Google Scholar
[16]	Liu J H, Xu Z H 2023 Phys. Rev. B 108 184205 Google Scholar
[17]	Lin Q, Li T Y, Xiao L, Wang K K, Yi W, Xue P 2022 Nat. Commun. 13 3229 Google Scholar
[18]	Hatano N, Nelson D R 1996 Phys. Rev. Lett. 77 570 Google Scholar
[19]	Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651 Google Scholar
[20]	Zhou L W, Wang Q H, Wang H L, Gong J B 2018 Phys. Rev. A 98 022129 Google Scholar
[21]	Zhou L W, Gong J B 2018 Phys. Rev. A 97 063603 Google Scholar
[22]	Tiwari V, Bhakuni D S, Sharma A 2024 Phys. Rev. B 109 L161104 Google Scholar
[23]	Ji C R, Zhou S D, Xie A, Jiang Z Y, Sheng X H, Ding L, Ke Y G, Wang H Q, Zhuang S L 2023 Phys. Rev. B 108 054310 Google Scholar
[24]	Mukherjee B, Sen A, Sen D, Sengupta K 2016 Phys. Rev. B 94 155122 Google Scholar
[25]	Mukherjee B, Mohan P, Sen D, Sengupta K 2018 Phys. Rev. B 97 205415 Google Scholar
[26]	Mukherjee B 2018 Phys. Rev. B 98 235112 Google Scholar
[27]	Yang K, Zhou L W, Ma W C, Kong X, Wang P F, Qin X, Rong X, Wang Y, Shi F Z 2019 Phys. Rev. B 100 085308 Google Scholar
[28]	Zhou L W, Du Q Q 2021 New J. Phys. 23 063041 Google Scholar
[29]	Zhou L W 2019 Phys. Rev. B 100 184314 Google Scholar
[30]	Else D V, Bauer B, Nayak C 2016 Phys. Rev. Lett. 117 090402 Google Scholar
[31]	Mukherjee B, Nandy S, Sen A, Sen D, Sengupta K 2020 Phys. Rev. B 101 245107 Google Scholar
[32]	Mukherjee B, Sen A, Sen D, Sengupta K 2020 Phys. Rev. B 102 014301 Google Scholar
[33]	Liu H, Xiong T S, Zhang W, An J H 2019 Phys. Rev. A 100 023622 Google Scholar
[34]	Wu H, An J H 2020 Phys. Rev. B 102 041119 Google Scholar
[35]	Wu H, An J H 2022 Phys. Rev. B 105 L121113 Google Scholar
[36]	Bai S Y, An J H 2020 Phys. Rev. A 102 060201 Google Scholar
[37]	Sarkar M, Ghosh R, Sen A, Sengupta K 2021 Phys. Rev. B 103 184309 Google Scholar
[38]	Sarkar M, Ghosh R, Sen A, Sengupta K 2022 Phys. Rev. B 105 024301 Google Scholar
[39]	Tong Q J, An J H, Gong J B, Luo H G, Oh C H 2013 Phys. Rev. B 87 201109 Google Scholar
[40]	Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett. 126 106803 Google Scholar
[41]	Ahmed A, Ramachandran A, Khaymovich I M, Sharma A 2022 Phys. Rev. B 106 205119 Google Scholar
[42]	Roy S, Khaymovich I M, Das A, Moessner R 2018 Sci. Post. Phys. 4 025 Google Scholar
[43]	成恩宏, 郎利君 2022 71 160301 Google Scholar Cheng E H, Lang L J 2022 Acta Phys. Sin. 71 160301 Google Scholar

施引文献

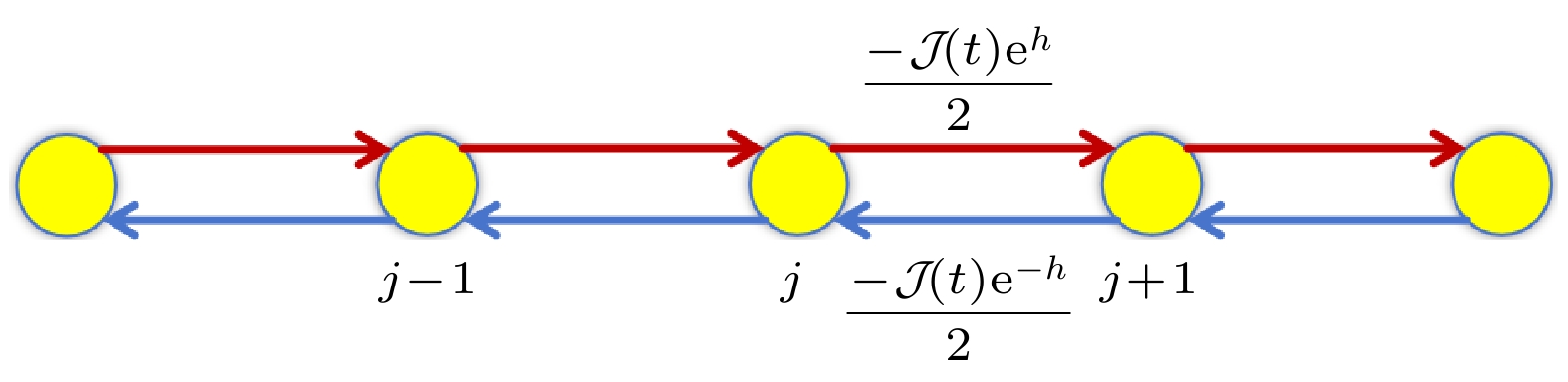
图 1 一维非互易模型示意图. 红线和蓝线代表不同跃迁强度, 其中$ \mathcal{J}(t) $如(1)式所示, $ h $ 代表非互易强度, $ j $代表格点

Fig. 1. Schematic diagram of the one-dimensional non-reciprocal model. The red and blue lines represent different hopping amplitudes, $ h $ is non-reciprocal amplitudes and $ j $ is the site index.

下载: 全尺寸图片幻灯片

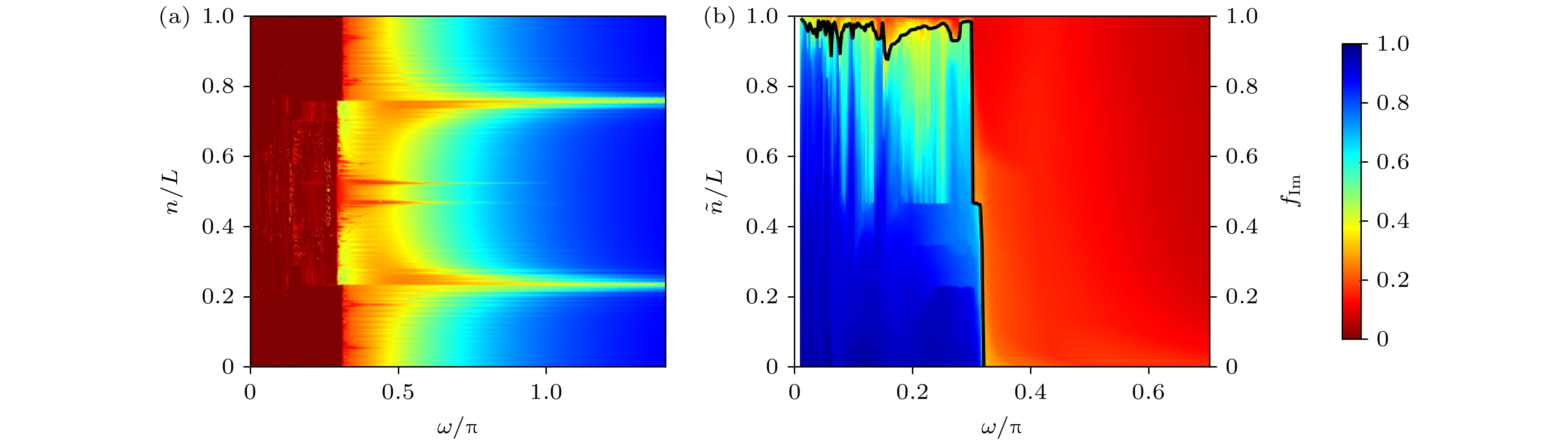
图 2 (a)逆参与率$ I^{(2)}_{n} $随着能级指标$ n/L $和频率$ \omega $的变化情况(这里, 能量实部升序排列). (b)分形维度$ D_{2} $随着能级指标$ \tilde{n}/L $和频率$ \omega $的变化情况, 以及复能量占比$ f_{\mathrm{Im}} $(黑色实线)随频率$ \omega $的变化图, 其中能级指标$ \tilde{n} $以逆参与率值的大小升序排列. 这里$ L=2048 $

Fig. 2. (a) Plot of $ I^{(2)}_{n} $ as a function of the normalized eigenfunction index $ n/L $ and $ \omega $. Here, the real part of the eigenvalues is ordered in ascending order. (b) Plot of the fractal dimension $ D_{2} $ as a function of $ \tilde{n}/L $ and $ \omega $, and $ f_{\mathrm{Im}} $ (solid black line) as a function of $ \omega $, where the energies sort in increasing order of the inverse participation ratio. Here, $ L=2048 $.

下载: 全尺寸图片幻灯片

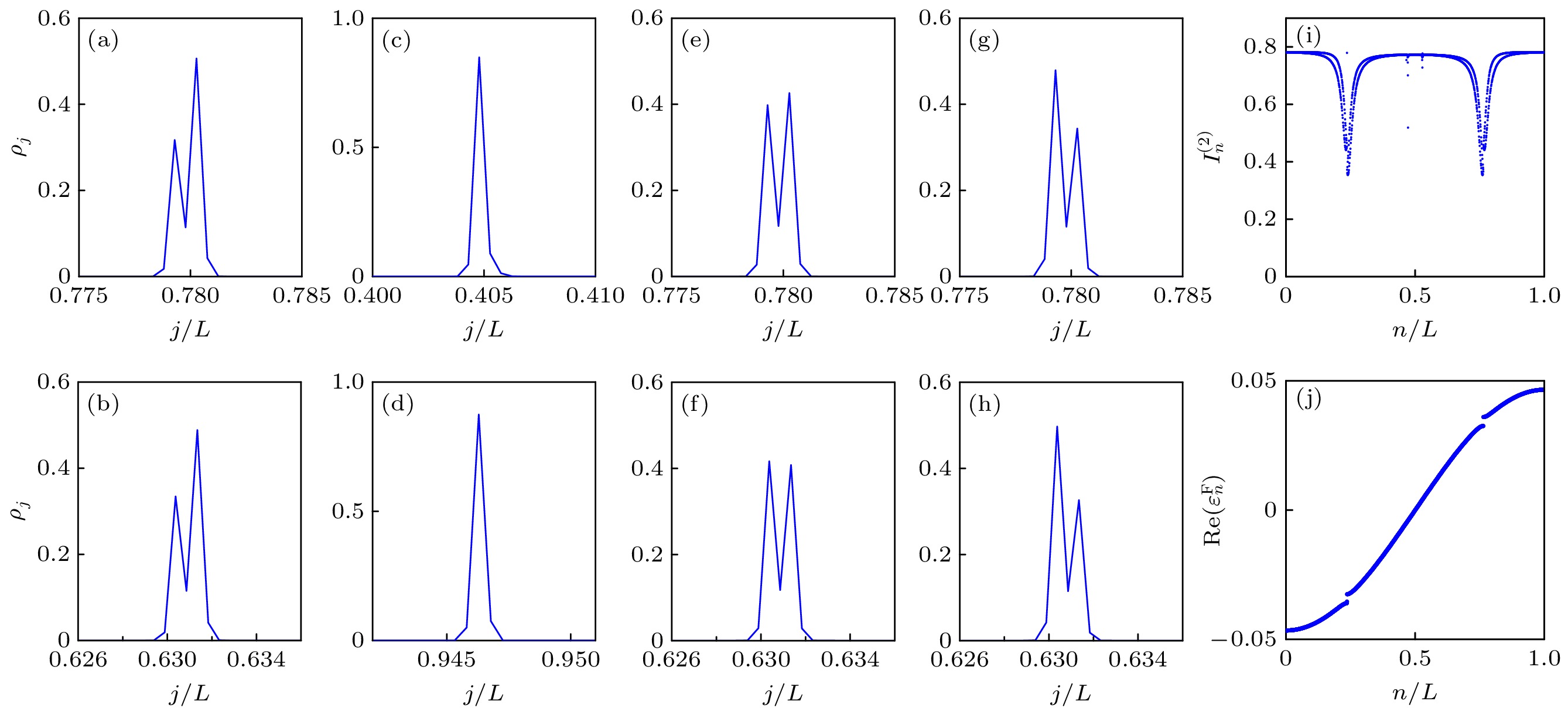
图 3 (a), (e)和(g) [(b), (f)和(h)]分别为$ h=0.1 $, 0和$ -0.1 $时, 位于能级$ n/L\approx0.24 $ ($ n/L\approx0.76 $)处的密度分布$ \rho_j $; (c)和(d)分别为$ h=0.1 $时, 能级$ n/L\approx1/3 $和$ 1/2 $处的密度分布$ \rho_j $; (i) $ I_n^{(2)} $随着能级$ n/L $变化的情况; (j) 能量实部$ \mathrm{Re}(\varepsilon_n^{{\mathrm{F}}}) $随着能级指标$ n/L $的分布情况. 这里选取 $ L=2048 $和$ \omega=\pi $, 并且能级指标按照能量实部升序排列

Fig. 3. (a), (e), and (g) [(b), (f), and (h)] Plot of the density distributions $ \rho_j $ at $ n/L\approx0.24 $ ($ n/L\approx0.76 $) with $ h=0.1 $, 0, and $ -0.1 $, respectively; (c) and (d) plot of $ \rho_j $ with $ h=0.1 $ at $ n/L\approx1/3 $ and $ 1/2 $, respectively; (i) $ I_n^{(2)} $ as a function of $ n/L $; (j) plot of $ \mathrm{Re}(\varepsilon_n^{{\mathrm{F}}}) $ as a function of $ n/L $. Here, $ L=2048 $, $ \omega=\pi $, and the real part of eigenvalues is ordered in ascending order.

下载: 全尺寸图片幻灯片

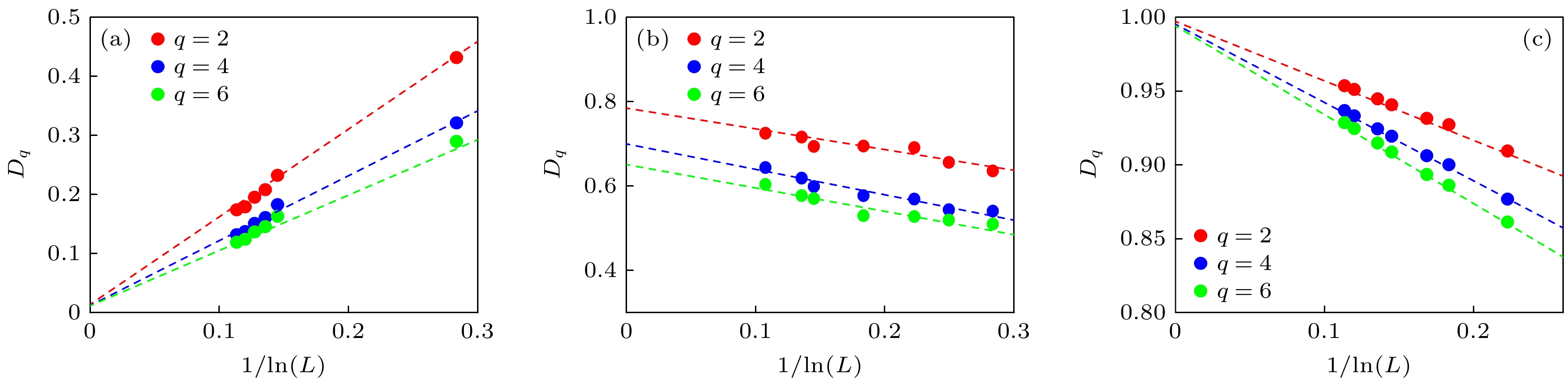
图 4 (a)—(c)分别展示了在频率$ \omega=0.235\pi $时, 能级$ \tilde{n}/L\approx 0.995 $, $ 0.7 $和$ 0.2 $处对应于不同$ q $的分形维度$ D_q $随着尺寸$ 1/\ln{(L)} $的变化情况. 这里能级按照逆参与率值的升序排列

Fig. 4. (a)–(c) Plot of the fractal dimensions $ D_q $ as a function of $ 1/\ln{(L)} $ with different $ q $ and $ \omega=0.235\pi $ at $ \tilde{n}/L\approx 0.995 $, $ 0.7 $, and $ 0.2 $, respectively. Here, the energies sort in increasing order of the inverse participation ratio.

下载: 全尺寸图片幻灯片

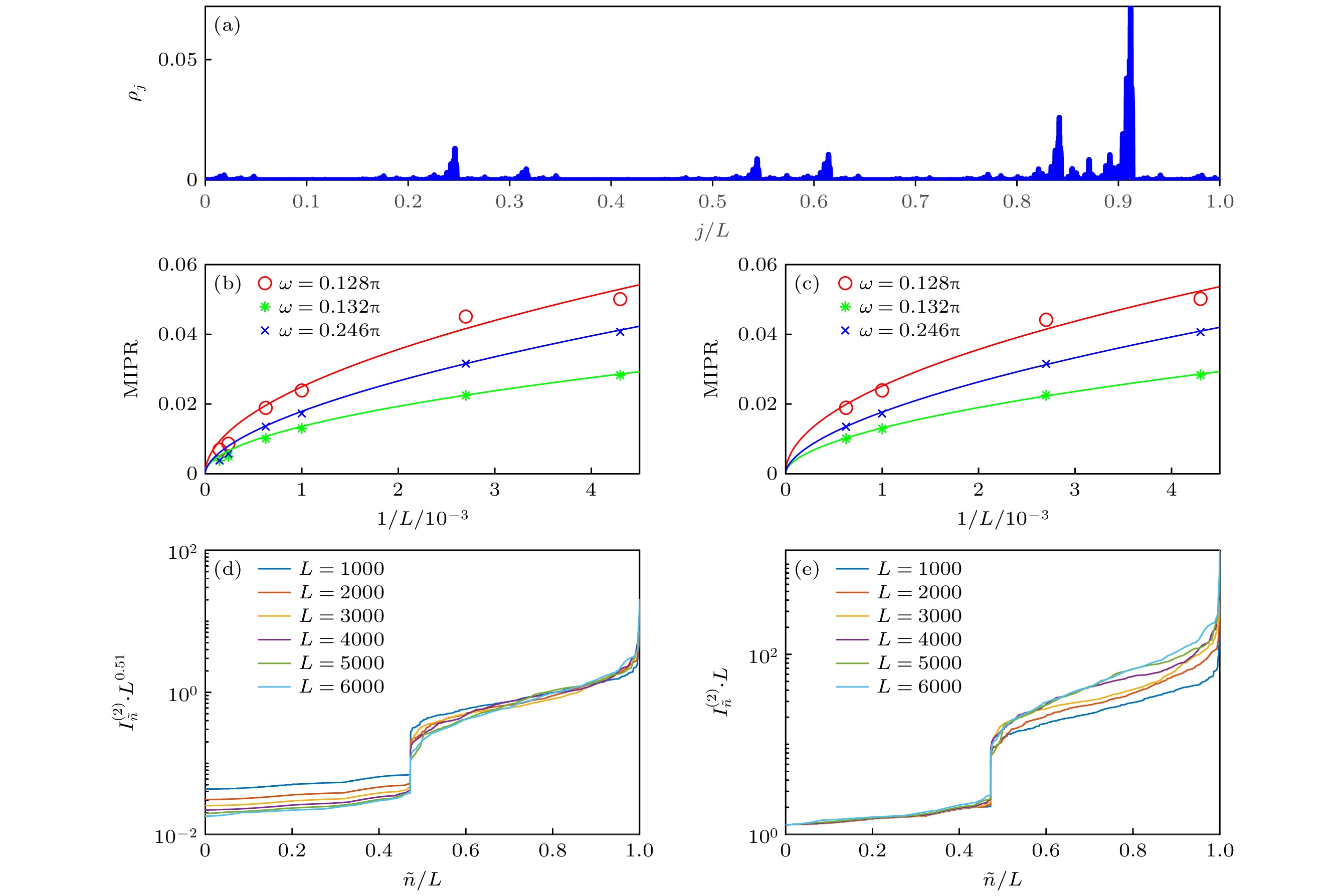
图 5 (a)频率$ \omega=0.132\pi $时, $ \tilde{n}/L=0.75 $处波函数的密度分布$ \rho_j $; (b)不同频率处, MIPR的标度分析; (c)图(b)频率下, 在参数$ h=0.1 $和$ \mu=0.05 $附近随机选取20个数进行无序平均后, MIPR的标度分析; (d), (e)频率$ \omega=0.132\pi $时, $ I_{\tilde{n}}^{(2)}\cdot L^{0.51} $与$ I_{\tilde{n}}^{(2)}\cdot L $随不同尺寸的缩放图. 这里能级按照逆参与率值的升序排列

Fig. 5. (a) Density distribution $ \rho_j $ with $ \omega=0.132\pi $ at $ \tilde{n}/L=0.75 $; (b) the scaling of the MIPR for different $ \omega $; (c) the scaling of MIPR after averaging random 20 parameters near $ h = 0.1 $ and $ \mu = 0.05 $ with the frequency in panel (b); (d), (e) the scaling of $ I_{\tilde{n}}^{(2)}\cdot L^{0.51} $ and $ I_{\tilde{n}}^{(2)}\cdot L $ as a function of $ L $ with $ \omega=0.132\pi $. Here, the energies sort in increasing order of the inverse participation ratio.

下载: 全尺寸图片幻灯片

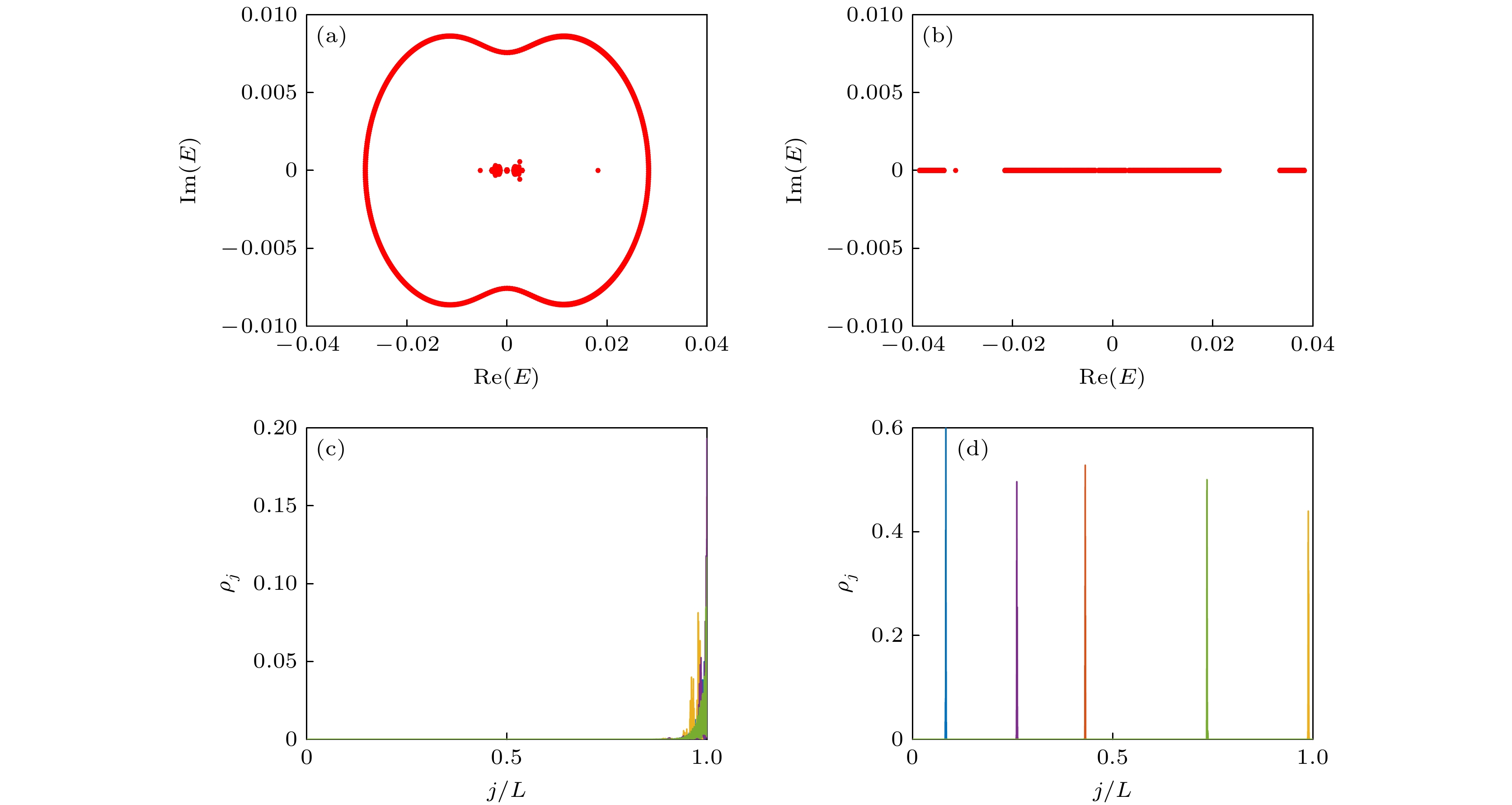
图 6 频率$ \omega=0.132\pi $ (a)和$ \omega=0.5\pi $ (b)时在复空间的能谱图; (c)在开边界条件下, 当频率$ \omega=0.132\pi $时环上随机5个能级所对应的密度分布$ \rho_j $; (d)在开边界条件下, 当频率$ \omega=0.5\pi $时随机5个能级所对应的密度分布$ \rho_j $, 这里$ L=2048 $

Fig. 6. Energy spectrum with $ \omega=0.132\pi $ (a) and $ \omega=0.5\pi $ (b) in complex space; (c) the density distribution $ \rho_j $ for 5 random energy levels on the ring under open boundary conditions with frequency $ \omega = 0.132\pi $; (d) the density distribution $ \rho_j $ for 5 random energy levels under open boundary conditions with frequency $ \omega = 0.5\pi $. Here, $ L=2048 $.

下载: 全尺寸图片幻灯片

map

[1]	Anderson P W 1958 Phys. Rev. 109 1492 Google Scholar
[2]	Tang L Z, Zhang G Q, Zhang L F, Zhang D W 2021 Phys. Rev. A 103 033325 Google Scholar
[3]	Schulz M, Hooley C A, Moessner R, Pollmann F 2019 Phys. Rev. Lett. 122 040606 Google Scholar
[4]	Lin X S, Chen X M, Guo G C, Gong M 2023 Phys. Rev. B 108 174206 Google Scholar
[5]	Dai Q, Lu Z P, Xu Z H 2023 Phys. Rev. B 108 144207 Google Scholar
[6]	Liu H, Lu Z P, Xia X, Xu Z H 2024 New J. Phys. 26 093007 Google Scholar
[7]	Li H, Dong Z L, Longhi S, Liang Q, Xie D Z, Yan B 2022 Phys. Rev. Lett. 129 220403 Google Scholar
[8]	Ganeshan S, Pixley J H, Das Sarma S 2015 Phys. Rev. Lett. 114 146601 Google Scholar
[9]	Aditya S, Sengupta K, Sen D 2023 Phys. Rev. B 107 035402 Google Scholar
[10]	Qi R, Cao J P, Jiang X P 2023 Phys. Rev. B 107 224201 Google Scholar
[11]	Zuo Z W, Kang D W 2022 Phys. Rev. A 106 013305 Google Scholar
[12]	Xu Z H, Xia X, Chen S 2021 Phys. Rev. B 104 224204 Google Scholar
[13]	Wang Y C, Xia X, Zhang L, Yao H P, Chen S, You J G, Zhou Q, Liu X J 2020 Phys. Rev. Lett. 125 196604 Google Scholar
[14]	Tang Q Y, He Y 2024 Phys. Rev. B 109 224204 Google Scholar
[15]	Zhou L W 2021 Phys. Rev. Res. 3 033184 Google Scholar
[16]	Liu J H, Xu Z H 2023 Phys. Rev. B 108 184205 Google Scholar
[17]	Lin Q, Li T Y, Xiao L, Wang K K, Yi W, Xue P 2022 Nat. Commun. 13 3229 Google Scholar
[18]	Hatano N, Nelson D R 1996 Phys. Rev. Lett. 77 570 Google Scholar
[19]	Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651 Google Scholar
[20]	Zhou L W, Wang Q H, Wang H L, Gong J B 2018 Phys. Rev. A 98 022129 Google Scholar
[21]	Zhou L W, Gong J B 2018 Phys. Rev. A 97 063603 Google Scholar
[22]	Tiwari V, Bhakuni D S, Sharma A 2024 Phys. Rev. B 109 L161104 Google Scholar
[23]	Ji C R, Zhou S D, Xie A, Jiang Z Y, Sheng X H, Ding L, Ke Y G, Wang H Q, Zhuang S L 2023 Phys. Rev. B 108 054310 Google Scholar
[24]	Mukherjee B, Sen A, Sen D, Sengupta K 2016 Phys. Rev. B 94 155122 Google Scholar
[25]	Mukherjee B, Mohan P, Sen D, Sengupta K 2018 Phys. Rev. B 97 205415 Google Scholar
[26]	Mukherjee B 2018 Phys. Rev. B 98 235112 Google Scholar
[27]	Yang K, Zhou L W, Ma W C, Kong X, Wang P F, Qin X, Rong X, Wang Y, Shi F Z 2019 Phys. Rev. B 100 085308 Google Scholar
[28]	Zhou L W, Du Q Q 2021 New J. Phys. 23 063041 Google Scholar
[29]	Zhou L W 2019 Phys. Rev. B 100 184314 Google Scholar
[30]	Else D V, Bauer B, Nayak C 2016 Phys. Rev. Lett. 117 090402 Google Scholar
[31]	Mukherjee B, Nandy S, Sen A, Sen D, Sengupta K 2020 Phys. Rev. B 101 245107 Google Scholar
[32]	Mukherjee B, Sen A, Sen D, Sengupta K 2020 Phys. Rev. B 102 014301 Google Scholar
[33]	Liu H, Xiong T S, Zhang W, An J H 2019 Phys. Rev. A 100 023622 Google Scholar
[34]	Wu H, An J H 2020 Phys. Rev. B 102 041119 Google Scholar
[35]	Wu H, An J H 2022 Phys. Rev. B 105 L121113 Google Scholar
[36]	Bai S Y, An J H 2020 Phys. Rev. A 102 060201 Google Scholar
[37]	Sarkar M, Ghosh R, Sen A, Sengupta K 2021 Phys. Rev. B 103 184309 Google Scholar
[38]	Sarkar M, Ghosh R, Sen A, Sengupta K 2022 Phys. Rev. B 105 024301 Google Scholar
[39]	Tong Q J, An J H, Gong J B, Luo H G, Oh C H 2013 Phys. Rev. B 87 201109 Google Scholar
[40]	Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett. 126 106803 Google Scholar
[41]	Ahmed A, Ramachandran A, Khaymovich I M, Sharma A 2022 Phys. Rev. B 106 205119 Google Scholar
[42]	Roy S, Khaymovich I M, Das A, Moessner R 2018 Sci. Post. Phys. 4 025 Google Scholar
[43]	成恩宏, 郎利君 2022 71 160301 Google Scholar Cheng E H, Lang L J 2022 Acta Phys. Sin. 71 160301 Google Scholar

[1]	郝佳鑫, 徐志浩. 复相互作用调制的两粒子系统中的局域化转变. , 2025, 74(6): 067201. doi: 10.7498/aps.74.20241691
[2]	冯曦曦, 陈文, 高先龙. 量子信息中的度量空间方法在准周期系统中的应用. , 2024, 73(4): 040501. doi: 10.7498/aps.73.20231605
[3]	刘辉, 陆展鹏, 徐志浩. 一维非厄米十字晶格中的退局域-局域转变. , 2024, 73(13): 137201. doi: 10.7498/aps.73.20240510
[4]	陆展鹏, 徐志浩. 具有平带的一维十字型晶格中重返局域化现象. , 2024, 73(3): 037202. doi: 10.7498/aps.73.20231393
[5]	任国梁, 申开波, 刘永佳, 刘英光. 类石墨烯氮化碳结构(C₃N)热传导机理研究. , 2023, 72(1): 013102. doi: 10.7498/aps.72.20221441
[6]	吴瑾, 陆展鹏, 徐志浩, 郭利平. 由超辐射引起的迁移率边和重返局域化. , 2022, 71(11): 113702. doi: 10.7498/aps.71.20212246
[7]	徐志浩, 皇甫宏丽, 张云波. 一维准周期晶格中玻色子对的迁移率边. , 2019, 68(8): 087201. doi: 10.7498/aps.68.20182218
[8]	王子, 张丹妹, 任捷. 声子系统中弹性波与热输运的拓扑与非互易现象. , 2019, 68(22): 220302. doi: 10.7498/aps.68.20191463
[9]	刘通, 高先龙. 具有p波超流的一维非公度晶格中迁移率边研究. , 2016, 65(11): 117101. doi: 10.7498/aps.65.117101
[10]	丁锐, 金亚秋, 小仓久直. 二维随机介质中柱面波传播及其局域性的随机泛函分析. , 2010, 59(6): 3674-3685. doi: 10.7498/aps.59.3674
[11]	曹永军, 杨旭, 姜自磊. 弹性波通过一维复合材料系统的透射性质. , 2009, 58(11): 7735-7740. doi: 10.7498/aps.58.7735
[12]	王慧琴, 刘正东, 王冰. 二维随机介质中的能量分布和频谱特性. , 2008, 57(9): 5550-5557. doi: 10.7498/aps.57.5550
[13]	王慧琴, 刘正东, 王冰. 同材质颗粒不同填充密度的随机介质中光场的空间分布. , 2008, 57(4): 2186-2191. doi: 10.7498/aps.57.2186
[14]	曹永军, 杨旭. 广义Fibonacci准周期结构声子晶体透射性质的研究. , 2008, 57(6): 3620-3624. doi: 10.7498/aps.57.3620
[15]	周文政, 林铁, 商丽燕, 黄志明, 崔利杰, 李东临, 高宏玲, 曾一平, 郭少令, 桂永胜, 褚君浩. InAlAs/InGaAs/InAlAs量子阱高迁移率二维电子气系统中的反弱局域效应研究. , 2007, 56(7): 4099-4104. doi: 10.7498/aps.56.4099
[16]	曹永军, 董纯红, 周培勤. 一维准周期结构声子晶体透射性质的研究. , 2006, 55(12): 6470-6475. doi: 10.7498/aps.55.6470
[17]	王传奎, 孙金祚, 王继锁, 王文正. 一维无公度系统Aubry模型的迁移率边. , 1993, 42(1): 95-100. doi: 10.7498/aps.42.95
[18]	庞根弟, 蔡建华. 非均匀无序系统的声子局域化. , 1988, 37(4): 688-690. doi: 10.7498/aps.37.688
[19]	刘有延, 周义昌. 一维无公度势系统的迁移率边. , 1988, 37(11): 1807-1813. doi: 10.7498/aps.37.1807
[20]	熊诗杰, 蔡建华. 非均匀无序系统中Anderson局域化的标度理论——实空间重整化群途径. , 1985, 34(12): 1530-1538. doi: 10.7498/aps.34.1530

计量

文章访问数: 455
PDF下载量: 33
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

周期驱动非互易Aubry-André模型中的多重分形态和迁移率边