-
相较于经典的傅里叶定律, 声子水动力学模型在描述纳米尺度超快声子热输运中已经展现出显著优势. 全环绕栅极晶体管(GAAFET)通过三维沟道设计极大优化了电学性能, 但其纳米尺度特征也导致自热问题和局部过热的挑战. 基于此, 本文针对纳米尺度GAAFET器件内的声子热传输特性开展理论和数值模拟分析. 首先, 基于声子玻尔兹曼方程严格推导了声子水动力学模型和边界条件, 建立了基于有限元的数值求解手段, 针对新型的GAAFET器件, 分析了表面粗糙度、沟道长度、沟道半径、栅极电介质、界面热阻等因素对其热传输特性的影响规律. 研究结果表明, 本文构建的连续介质框架下基于声子水动力学模型及温度跳跃条件的非傅里叶热分析方法能够精确预测GAAFET内部非傅里叶声子导热过程, 并揭示声子阻尼散射和声子/界面散射的作用机制. 这项工作为进一步优化GAAFET的热可靠性设计, 提高其热稳定性和工作性能提供了重要的理论支持.Compared to the classical Fourier’s law, the phonon hydrodynamic model has demonstrated significant advantages in describing ultrafast phonon heat transport at the nanoscale. The gate-all-around field-effect transistor (GAAFET) greatly optimizes its electrical performance through its three-dimensional channel design, but its nanoscale characteristics also lead to challenges such as self-heating and localized overheating. Therefore, it is of great significance to study the internal heat transport mechanism of GAAFET devices to obtain the thermal process and heat distribution characteristics. Based on this, this paper conducts theoretical and numerical simulation analyses on the phonon heat transfer characteristics within nanoscale GAAFET devices. Firstly, based on the phonon Boltzmann equation, the phonon hydrodynamic model and boundary conditions are rigorously derived, establishing a numerical solution method based on finite elements. For the novel GAAFET devices, the effects of factors such as surface roughness, channel length, channel radius, gate dielectric, and interface thermal resistance on their heat transfer characteristics are analyzed. The research results indicate that the larger the surface roughness, the smaller the channel length and the channel radius, the larger the interface thermal resistance leads to the higher hot spot peak temperature. The non-Fourier heat analysis method based on the phonon hydrodynamic model and temperature jump condition within the continuous medium framework constructed in this paper can accurately predict the non-Fourier phonon heat conduction process inside GAAFET and reveal the mechanisms of resistive scattering and phonon/interface scattering. This work provides important theoretical support for further optimizing the thermal reliability design of GAAFET, improving its thermal stability, and operational performance.
-
Keywords:
- gate-all-around field-effect transistor /
- phonon hydrodynamic model /
- temperature jump /
- non-Fourier thermal analysis
[1] Liu S Q, Li Q H, Yang C, Yang J, Xu L, Xu L Q, Ma J C, Li Y, Fang S B, Wu B C, Dong J C, Yang J B, Lu J 2022 Phys. Rev. Appl. 18 054089
Google Scholar
[2] Yoon J S, Rim T, Kim J, Meyyappan M, Baek C K, Jeong Y H 2014 Appl. Phys. Lett. 105 102105
Google Scholar
[3] Zhang Q Z, Yin H X, Meng L K, Yao J X, Li J J, Wang G L, Li Y D, Wu Z H, Xiong W J, Yang H, Tu H L, Li J F, Zhao C, Wang W W, Ye T C 2018 IEEE Electron Device Lett. 39 464
Google Scholar
[4] Belkhiria M, Echouchene F, Jaba N, Bajahzar A, Belmabrouk H 2021 IEEE Trans. Electron Devices 68 954
Google Scholar
[5] Belkhiria M, Alyousef H A, Chehimi H, Aouaini F, Echouchene F 2022 Thin Solid Films 758 139423
Google Scholar
[6] Rezgui H, Mukherjee C, Wang Y, Deng M, Kumar A, Müller J, Larrieu G, Maneux C 2023 IEEE Trans. Electron Devices 70 6505
Google Scholar
[7] Myeong I, Son D, Kim H, Shin H 2019 IEEE Trans. Electron Devices 66 4631
Google Scholar
[8] Chhabria V A, Sapatnekar S S 2019 20th International Symposium on Quality Electronic Design (ISQED). pp235–240
[9] Alvarez P T 2018 Thermal Transport in Semiconductors: First Principles and Phonon Hydrodynamics (1st Ed.) (Switzerland: Springer) pp41–71
[10] Yang N, Zhang G, Li B W 2010 Nano Today 5 85
Google Scholar
[11] Guo Y Y, Wang M R 2016 J. Comput. Phys. 315 1
Google Scholar
[12] Ran X, Guo Y Y, Wang M R 2018 Int. J. Heat Mass Transfer 123 616
Google Scholar
[13] Zhang C, Guo Z L 2021 Int. J. Heat Mass Tranfer 181 121847
Google Scholar
[14] Cattaneo C 1948 Atti Sem. Mat. Fis. Univ. Modena 3 83
[15] Vernotte P 1958 Comptes Rendus 246 3154
[16] Tzou D Y 1995 J. Heat Transfer 117 8
Google Scholar
[17] Xu M T, Wang L Q 2005 Int. J. Heat Mass Transfer 48 5616
Google Scholar
[18] Chen G 2002 J. Heat Transfer 124 320
Google Scholar
[19] Cao B Y, Guo Z Y 2007 J. Appl. Phys. 102 053503
Google Scholar
[20] Dong Y, Cao B Y, Guo Z Y 2011 J. Appl. Phys. 110 063504
Google Scholar
[21] Guyer R A, Krumhansl J A 1966 Phys. Rev. 148 766
Google Scholar
[22] Guyer R A, Krumhansl J A 1966 Phys. Rev. 148 778
Google Scholar
[23] Alvarez F X, Jou D, Sellitto A 2009 J. Appl. Phys. 105 014317
Google Scholar
[24] Hua Y C, Cao B Y 2014 Int. J. Heat Mass Tranfer 78 755
Google Scholar
[25] Kaiser J, Feng T L, Maassen J, Wang X F, Ruan X L, Lundstrom M 2017 J. Appl. Phys. 121 044302
Google Scholar
[26] Guo Y Y, Wang M R 2018 Phys. Rev. B 97 035421
Google Scholar
[27] Beardo A, Hennessy M G, Sendra L, Camacho J, Myers T G, Bafaluy J, Alvarez F X 2020 Phys. Rev. B 101 075303
Google Scholar
[28] Rezgui H, Nasri F, Ali A B H, Guizani A A 2020 IEEE Trans. Electron Devices 68 10
[29] Rezgui H, Nasri F, Ali A B H, Guizani A A 2021 Therm. Sci. Eng. Prog. 25 100938
Google Scholar
[30] Chen G 2005 Nanoscale Energy Transport and Conversion: a Parallel Treatment of Electrons, Molecules, Phonons, and Photons (New York: Oxford University Press) pp227–275
[31] Peierls R E 1996 Quantum Theory of Solids (Oxford: Clarendon Press) pp45–52
[32] Chen N X, Sun B H 2017 Chin. Phys. Lett. 34 020502
Google Scholar
[33] Aissa M F B, Nasri F, Belmabrouk H 2017 IEEE Trans. Electron Devices 64 5236
Google Scholar
[34] Sellitto A, Carlomagno I, Jou D 2015 Proc. R. Soc. A 471 20150376
Google Scholar
[35] Beardo A, Calvo-Schwarzwälder M, Camacho J, Myers T, Torres P, Sendra L, Alvarez F, Bafaluy J 2019 Phys. Rev. Appl. 11 034003
Google Scholar
[36] Zhang Z M 2020 Nano/microscale Heat Transfer (2nd Ed.) (Switzerland: Springer) p235
[37] Mahajan S S, Subbarayan G, Sammakia B G 2011 IEEE Trans. Compon. Packag. Manuf. Technol. 1 1132
Google Scholar
[38] Chen G F, Hu B Y, Jiang Z L, Wang Z L, Tang D W 2023 Int. J. Heat Mass Tranfer 202 123676
Google Scholar
[39] Lai J H, Su Y L, Bu J H, Li B H, Li B, Zhang G H 2020 IEEE Trans. Electron Devices 67 4060
Google Scholar
[40] The Chinese Academy of Sciences 2022 Thermal Management of Electronic Devices p2 (in Chinses) [中国科学院 2022 电子设备热管理 (北京: 科学出版社) 第2页]
The Chinese Academy of Sciences 2022 Thermal Management of Electronic Devices p2 (in Chinses)
[41] 程哲 2021 70 236502
Google Scholar
Cheng Z 2021 Acta Phys. Sin. 70 236502
Google Scholar
[42] Jeong J, Choi S J, Shim J, Kim E, Kim S K, Kim B H, Kim J P, Suh Y, Beak W J, Geum D, Koh Y, Kim D, Kim S 2023 2023 International Electron Devices Meeting (IEDM) pp1–4
-
图 1 (a)二维稳态声子导热问题的无量纲温度分布; (b)薄膜法向瞬态导热问题的无量纲温度分布. 符号为文献[11]的LBM结果, 实线为当前声子水动力学方程的模拟结果
Fig. 1. (a) Dimensionless temperature distribution of the two-dimensional steady-state phonon thermal conductivity problem; (b) dimensionless temperature distribution of the normal transient thermal conductivity problem of the thin film. The symbols represent the LBM results in Ref.[11], and the solid lines represent the simulation results of current phonon hydrodynamics equation.
图 2 (a)三维GAAFET的结构示意图; (b)二维轴对称结构
Fig. 2. (a) Schematic diagram of three-dimensional GAAFET structure; (b) two-dimensional axisymmetric structure.
图 3 $ t=30\; {\rm{ps}} $时刻GAAFET器件的表面温度分布 (a) $ p = $$ 0 $; (b) $ p = 0.1 $; (c) $ p = 1 $
Fig. 3. Temperature distribution of GAAFET devices at $ t=30\; {\rm{ps}} $: (a) $ p = 0 $; (b) $ p = 0.1 $; (c) $ p = 1 $.
图 4 $ t=50\; {\rm{ps}} $时刻GAAFET器件的等温线图 (a) $ p = $$ 0.2 $; (b) $ p = 0.4 $; (c) $ p = 0.6 $
Fig. 4. 2D Isotherm cloud maps of GAAFET devices at $ t=50\; {\rm{ps}} $: (a) $ p = 0.2 $; (b) $ p = 0.4 $; (c) $ p = 0.6 $.
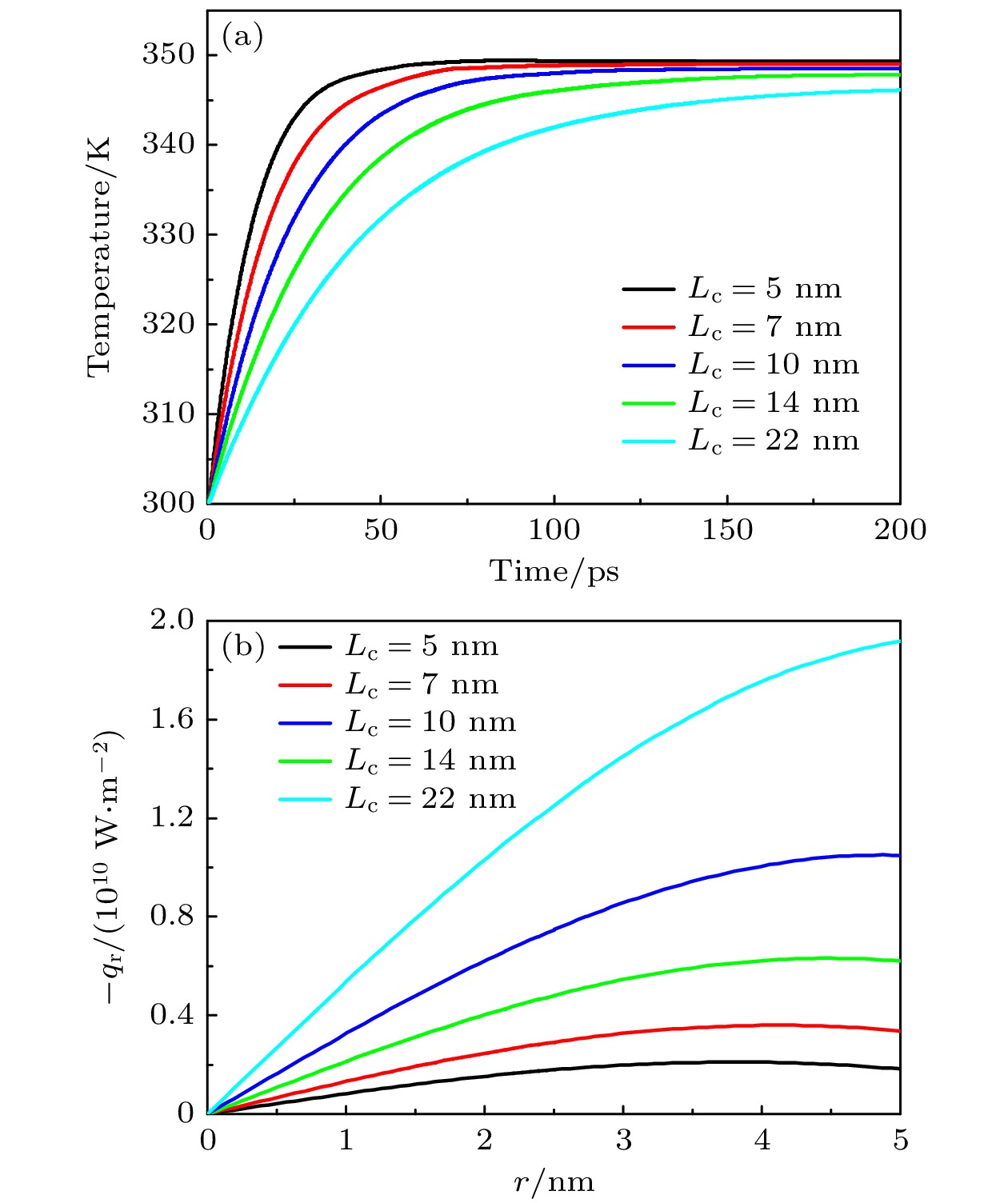
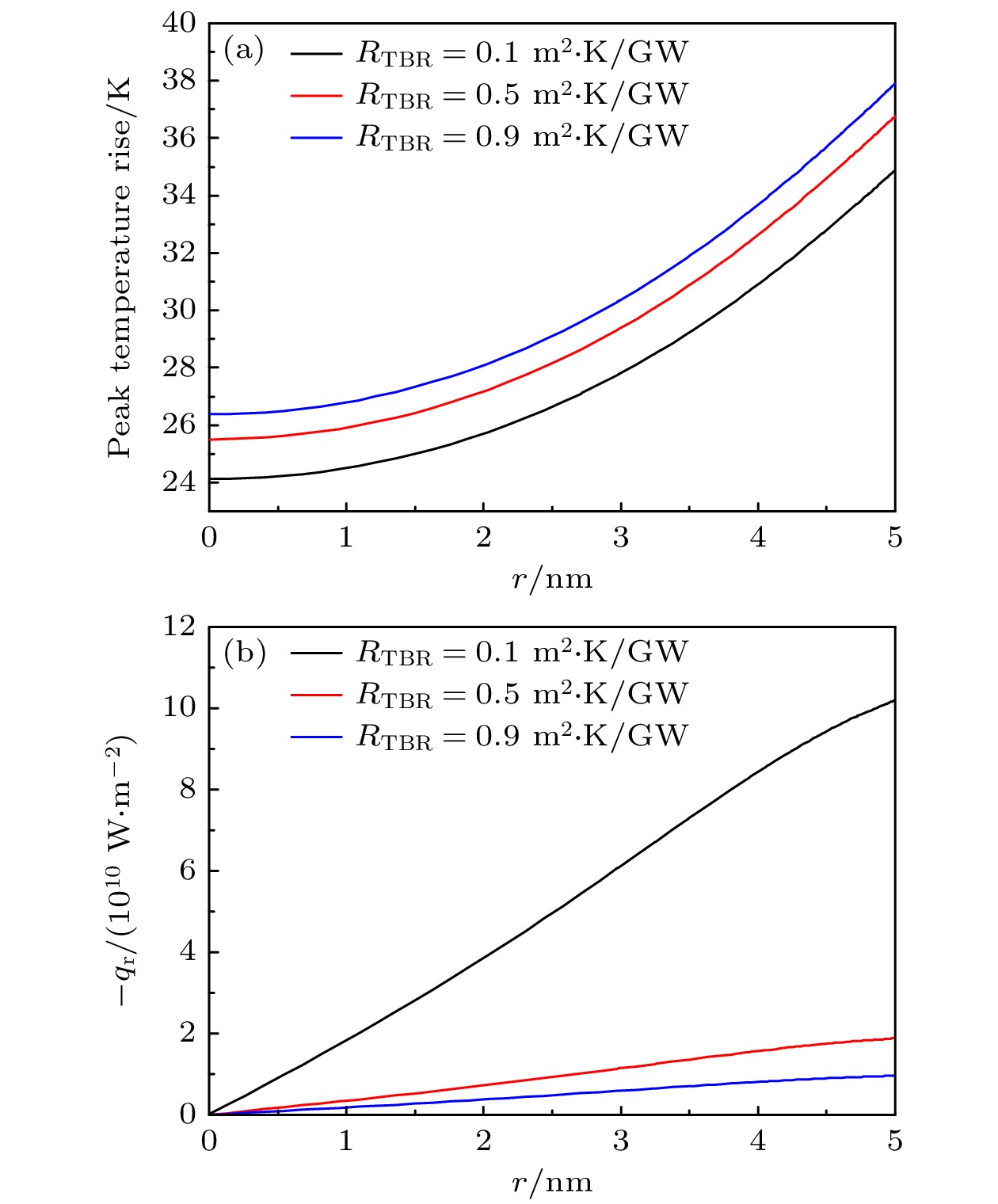
图 5 不同沟道长度的GAAFET器件的温度和热流密度变化 (a) 硅/氧化物界面中点处温度峰值的时间演变; (b) $ t= $$ 200\; {\rm{ps}} $时刻沿r方向中线上的径向热流密度分布
Fig. 5. Temperature and heat flux changes of GAAFET devices with different channel lengths: (a) Time evolution of temperature peak at the midpoint of the silicon/oxide interface; (b) radial heat flux distribution along the centerline in the r-direction at $ t=200\; {\rm{ps}} $.
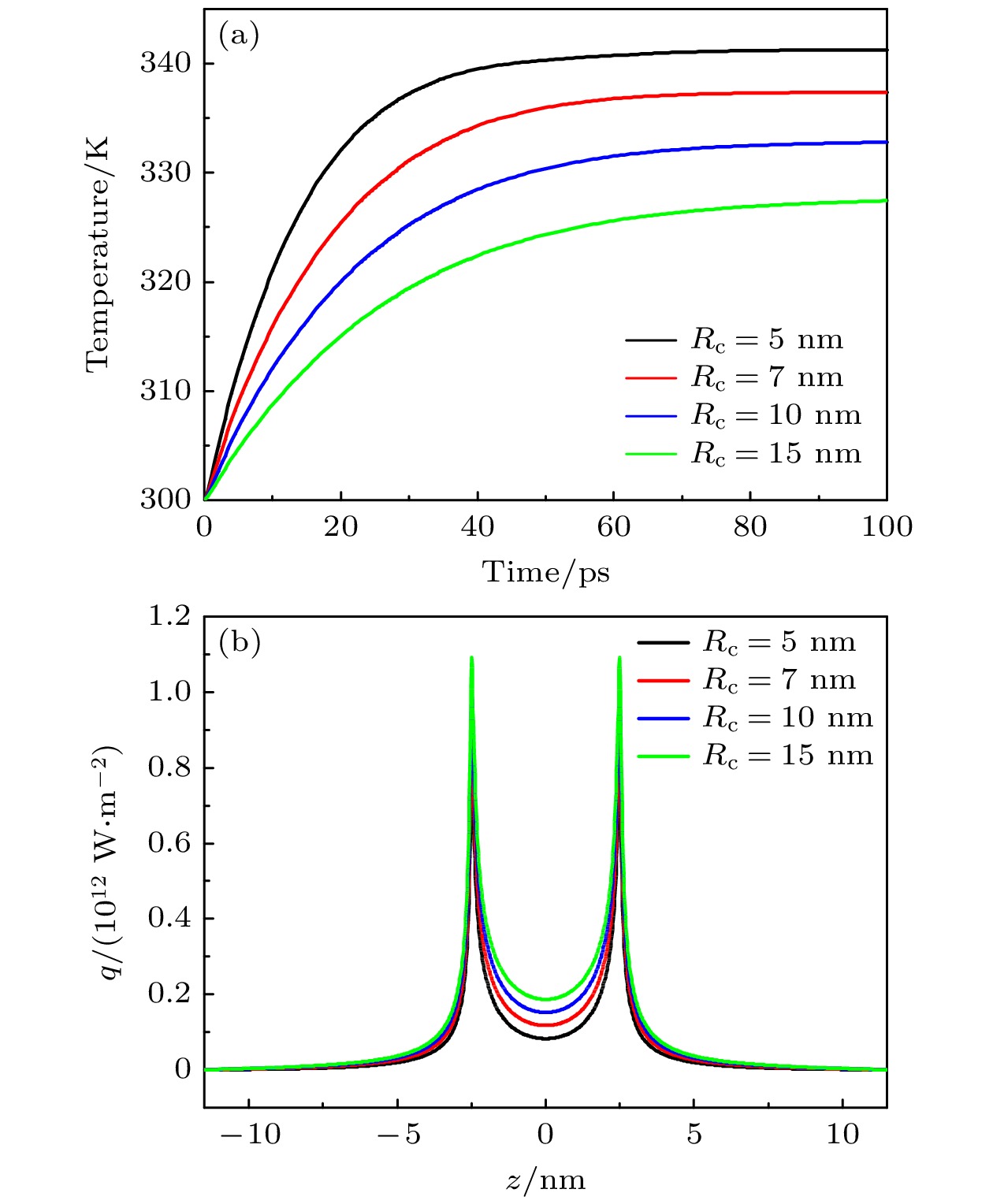
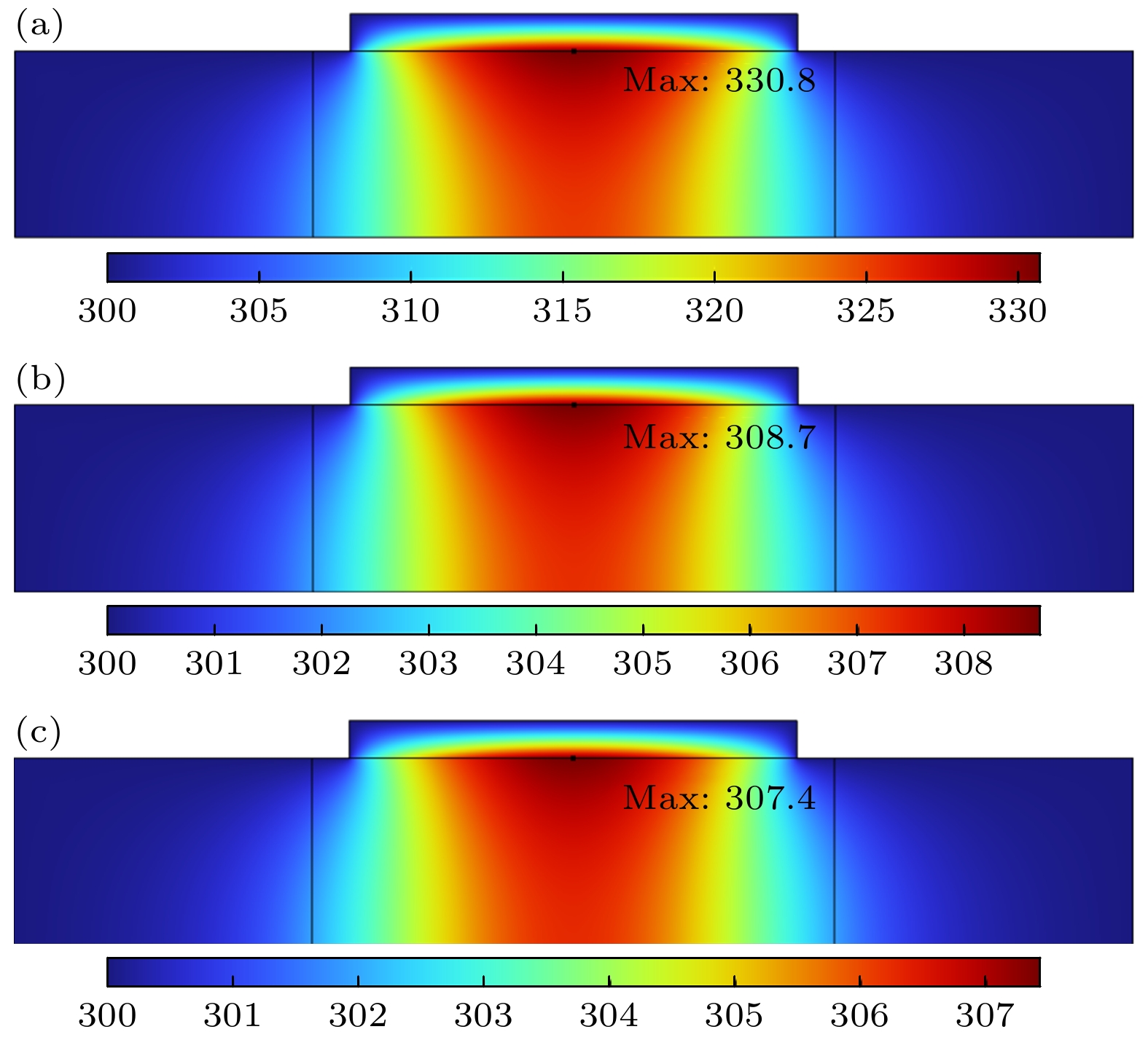
图 6 不同沟道半径的GAAFET器件的温度和热流密度变化 (a)硅/氧化物界面中点处温度峰值的时间演变; (b) $ t= $$ 50\; {\rm{ps}} $时刻沿氧化物-半导体界面沟道长度上的热流密度分布
Fig. 6. Temperature and heat flux variations of GAAFET devices with different channel radius. (a) Time evolution of peak temperature at the midpoint of the silicon/oxide interface; (b) the heat flux distribution along the channel length of the oxide semiconductor interface at time $ t=50\; {\rm{ps}} $.
图 7 不同栅极电介质材料的GAAFET器件的温度云图 (a) Si-$ {\rm{SiO}}_2 $; (b) Si-$ {\rm{Al}}_2{\rm{O}}_3 $; (c) Si-$ {\rm{HfO}}_2 $
Fig. 7. Temperature distribution of GAAFET devices with different gate dielectric materials: (a) Si-$ {\rm{SiO}}_2 $; (b) Si-$ {\rm{Al}}_2{\rm{O}}_3 $; (c) Si-$ {\rm{HfO}}_2 $.
图 8 $ t=100\; {\rm{ps}} $时不同热阻GAAFET沿r方向中线上的(a)温升和(b)径向热流密度变化
Fig. 8. (a) Temperature rise and (b) radial heat flux variation along the centerline of different thermal resistances GAAFET in the r-direction at $ t=100\; {\rm{ps}} $.
表 1 Si和介电材料(SiO2, Al2O3, HfO2)的热物性参数[28,37]
Table 1. Thermal physical property parameters of Si and dielectric materials (SiO2, Al2O3, HfO2)[28,37]
相关参数 Si $ {\rm{SiO}}_2 $ $ {\rm{HfO}}_2 $ $ {\rm{Al}}_2{\rm{O}}_3 $ $ {v_{\rm{g}}}/({\rm{m{\cdot} s^{-1}}}) $ 3000 5900 4800 8800 $ \kappa /({\rm{W{\cdot} m^{-1}{\cdot} K^{-1}}}) $ 150 1.4 1.0 1.5 $C/{\rm{(10^6 \;J{\cdot} }}{{\rm{m}}^{\rm{-3}}}{\rm{{\cdot} K^{-1})}} $ 1.50 1.75 2.71 2.65 $ \varLambda /{\rm{nm}} $ 100 0.4 0.23 0.19 $ {\tau_{\rm{R}}} = \varLambda /v/{\rm{ps}} $ 33.3 0.068 0.048 0.02 $ {R_{\rm{TBR}}}/{\rm{({m^2} {\cdot} K{\cdot} GW^{-1})}} $ — 0.1 9.03 6.92 
下载: 导出CSV
-
[1] Liu S Q, Li Q H, Yang C, Yang J, Xu L, Xu L Q, Ma J C, Li Y, Fang S B, Wu B C, Dong J C, Yang J B, Lu J 2022 Phys. Rev. Appl. 18 054089
Google Scholar
[2] Yoon J S, Rim T, Kim J, Meyyappan M, Baek C K, Jeong Y H 2014 Appl. Phys. Lett. 105 102105
Google Scholar
[3] Zhang Q Z, Yin H X, Meng L K, Yao J X, Li J J, Wang G L, Li Y D, Wu Z H, Xiong W J, Yang H, Tu H L, Li J F, Zhao C, Wang W W, Ye T C 2018 IEEE Electron Device Lett. 39 464
Google Scholar
[4] Belkhiria M, Echouchene F, Jaba N, Bajahzar A, Belmabrouk H 2021 IEEE Trans. Electron Devices 68 954
Google Scholar
[5] Belkhiria M, Alyousef H A, Chehimi H, Aouaini F, Echouchene F 2022 Thin Solid Films 758 139423
Google Scholar
[6] Rezgui H, Mukherjee C, Wang Y, Deng M, Kumar A, Müller J, Larrieu G, Maneux C 2023 IEEE Trans. Electron Devices 70 6505
Google Scholar
[7] Myeong I, Son D, Kim H, Shin H 2019 IEEE Trans. Electron Devices 66 4631
Google Scholar
[8] Chhabria V A, Sapatnekar S S 2019 20th International Symposium on Quality Electronic Design (ISQED). pp235–240
[9] Alvarez P T 2018 Thermal Transport in Semiconductors: First Principles and Phonon Hydrodynamics (1st Ed.) (Switzerland: Springer) pp41–71
[10] Yang N, Zhang G, Li B W 2010 Nano Today 5 85
Google Scholar
[11] Guo Y Y, Wang M R 2016 J. Comput. Phys. 315 1
Google Scholar
[12] Ran X, Guo Y Y, Wang M R 2018 Int. J. Heat Mass Transfer 123 616
Google Scholar
[13] Zhang C, Guo Z L 2021 Int. J. Heat Mass Tranfer 181 121847
Google Scholar
[14] Cattaneo C 1948 Atti Sem. Mat. Fis. Univ. Modena 3 83
[15] Vernotte P 1958 Comptes Rendus 246 3154
[16] Tzou D Y 1995 J. Heat Transfer 117 8
Google Scholar
[17] Xu M T, Wang L Q 2005 Int. J. Heat Mass Transfer 48 5616
Google Scholar
[18] Chen G 2002 J. Heat Transfer 124 320
Google Scholar
[19] Cao B Y, Guo Z Y 2007 J. Appl. Phys. 102 053503
Google Scholar
[20] Dong Y, Cao B Y, Guo Z Y 2011 J. Appl. Phys. 110 063504
Google Scholar
[21] Guyer R A, Krumhansl J A 1966 Phys. Rev. 148 766
Google Scholar
[22] Guyer R A, Krumhansl J A 1966 Phys. Rev. 148 778
Google Scholar
[23] Alvarez F X, Jou D, Sellitto A 2009 J. Appl. Phys. 105 014317
Google Scholar
[24] Hua Y C, Cao B Y 2014 Int. J. Heat Mass Tranfer 78 755
Google Scholar
[25] Kaiser J, Feng T L, Maassen J, Wang X F, Ruan X L, Lundstrom M 2017 J. Appl. Phys. 121 044302
Google Scholar
[26] Guo Y Y, Wang M R 2018 Phys. Rev. B 97 035421
Google Scholar
[27] Beardo A, Hennessy M G, Sendra L, Camacho J, Myers T G, Bafaluy J, Alvarez F X 2020 Phys. Rev. B 101 075303
Google Scholar
[28] Rezgui H, Nasri F, Ali A B H, Guizani A A 2020 IEEE Trans. Electron Devices 68 10
[29] Rezgui H, Nasri F, Ali A B H, Guizani A A 2021 Therm. Sci. Eng. Prog. 25 100938
Google Scholar
[30] Chen G 2005 Nanoscale Energy Transport and Conversion: a Parallel Treatment of Electrons, Molecules, Phonons, and Photons (New York: Oxford University Press) pp227–275
[31] Peierls R E 1996 Quantum Theory of Solids (Oxford: Clarendon Press) pp45–52
[32] Chen N X, Sun B H 2017 Chin. Phys. Lett. 34 020502
Google Scholar
[33] Aissa M F B, Nasri F, Belmabrouk H 2017 IEEE Trans. Electron Devices 64 5236
Google Scholar
[34] Sellitto A, Carlomagno I, Jou D 2015 Proc. R. Soc. A 471 20150376
Google Scholar
[35] Beardo A, Calvo-Schwarzwälder M, Camacho J, Myers T, Torres P, Sendra L, Alvarez F, Bafaluy J 2019 Phys. Rev. Appl. 11 034003
Google Scholar
[36] Zhang Z M 2020 Nano/microscale Heat Transfer (2nd Ed.) (Switzerland: Springer) p235
[37] Mahajan S S, Subbarayan G, Sammakia B G 2011 IEEE Trans. Compon. Packag. Manuf. Technol. 1 1132
Google Scholar
[38] Chen G F, Hu B Y, Jiang Z L, Wang Z L, Tang D W 2023 Int. J. Heat Mass Tranfer 202 123676
Google Scholar
[39] Lai J H, Su Y L, Bu J H, Li B H, Li B, Zhang G H 2020 IEEE Trans. Electron Devices 67 4060
Google Scholar
[40] The Chinese Academy of Sciences 2022 Thermal Management of Electronic Devices p2 (in Chinses) [中国科学院 2022 电子设备热管理 (北京: 科学出版社) 第2页]
The Chinese Academy of Sciences 2022 Thermal Management of Electronic Devices p2 (in Chinses)
[41] 程哲 2021 70 236502
Google Scholar
Cheng Z 2021 Acta Phys. Sin. 70 236502
Google Scholar
[42] Jeong J, Choi S J, Shim J, Kim E, Kim S K, Kim B H, Kim J P, Suh Y, Beak W J, Geum D, Koh Y, Kim D, Kim S 2023 2023 International Electron Devices Meeting (IEDM) pp1–4
下载:
计量
- 文章访问数: 590
- PDF下载量: 23
- 被引次数: 0
