-
复杂网络的高阶相互作用, 如单纯复形和超边等, 已经成为了研究的热点. 本文提出一种基于节点同步动力学的特性来重构网络的单纯复形结构的新方法. 通过分析Kuramoto-Sakaguchi模型中节点相位的时间序列同步性, 建立了网络拓扑结构的解析描述, 实现了对网络结构的精确辨识. 该方法的核心在于, 运用理论手段推导得到了拉普拉斯矩阵与线性化Kuramoto-Sakaguchi系统相位之间的解析联系. 这一联系不仅具有强大的普适性, 而且能够有效地应用于识别包含任意阶单纯复形相互作用的网络结构. 本文的研究进一步表明, 这种解析关系能够用于鉴别网络中的对称节点, 并且通过数值模拟证实了间接相互作用节点之间发生遥同步的现象与网络结构的对称性有着密切的联系. 这些发现为深入理解网络的结构特性和动力学行为提供了新的理论工具和视角.High-order interactions as exemplified by simplex and hyper-edge structures have emerged as a prominent area of interest in complex network research. These high-order interactions introduce much complexity into the interplay between nodes, which often require advanced analytical approaches to fully characterize the underlying network structures. For example, methods based on statistical dependencies have been proposed to identify high-order structures from multi-variate time series. In this work, we reconstruct the simplex structures of a network based on synchronization dynamics between network nodes. More specifically, we construct a topological structure of network by examining the temporal synchronization of phase time series data derived from the Kuramoto-Sakaguchi (KS) model. In addition, we show that there is an analytical relationship between the Laplacian matrix of the network and phase variables of the linearized KS model. Our method identifies structural symmetric nodes within a network, which therefore builds a correlation between node synchronization behavior and network’s symmetry. This representation allows for identifying high-order network structure, showing its advantages over statistical methods. In addition, remote synchronization is a complex dynamical process, where spatially separated nodes within a network can synchronize their states despite the lack of direct interaction. Furthermore, through numerical simulations, we observe the strong correlation between remote synchronization among indirectly interacting nodes and the network’s underlying symmetry. This finding reveals the intricate relationship between network structure and the dynamical process. In summary, we propose a powerful tool for analyzing complex networks, in particular uncovering the interplay between network structure and dynamics. We provide novel insights for further exploring and understanding the high-order interactions and the underlying symmetry of complex networks.
-
Keywords:
- complex network /
- simplex /
- phase synchronization /
- high order interaction
[1] Réka A, Albert-László B 2002 Rev. Mod. Phys. 74 47
Google Scholar
[2] Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D U 2006 Phys. Rep. 424 175
Google Scholar
[3] Federico B, Giulia C, Iacopo I, Vito L, Maxime L, Alice P, Jean-Gabriel Y Giovanni P 2020 Phys. Rep. 874 1
Google Scholar
[4] Hidetsugu S, Yoshiki K 1986 Prog. Theor. Phys. 76 576
Google Scholar
[5] Shinya W, Steven H S 1993 Phys. Rev. Lett. 70 2391
Google Scholar
[6] 张海峰, 王文旭 2020 69 088906
Google Scholar
Zhang H F, Wang W X 2020 Acta Phys. Sin. 69 088906
Google Scholar
[7] Wang W, Nie Y Y, Li W Y, Lin T, Shang M S, Su S, Tang Y, Zhang Y C 2024 Phys. Rep. 1056 1
Google Scholar
[8] Andrea F, Salvatore C, Giulio R 2023 App. Net. Sci. 8 31
Google Scholar
[9] Eyal Bairey, Eric D K, Roy K 2016 Nat. Commun. 7 12285
Google Scholar
[10] Nian F Z, Shi Y Y, Cao J 2021 J Comput. Sci.-Neth. 55 101438
Google Scholar
[11] Alessia A, Gennaro C, Vittorio S, Carmine S 2021 IEEE Access 9 140938
Google Scholar
[12] Marc T, Jose C 2014 J. Phys. A 47 343001
Google Scholar
[13] Marc T 2007 Phys. Rev. Lett. 98 224101
Google Scholar
[14] Yu D C, Marco R, Ljupco K 2006 Phys. Rev. Lett. 97 188701
Google Scholar
[15] Wang W X, Yang R, Lai Y C, Vassilios K, Celso G 2011 Phys. Rev. Lett. 106 154101
Google Scholar
[16] 徐翔, 朱承, 朱先强 2021 70 088901
Google Scholar
Xu X, Zhu C, Zhu X Q 2021 Acta Phys. Sin. 70 088901
Google Scholar
[17] Jose C, Mor N, Sarah H, Marc T 2017 Nat. Commun. 8 2192
Google Scholar
[18] Xiao N J, Zhou A F, Megan L. Kempher, Jason Z. Shi, Yuan M T, Guo X, Wu L W, Ning D L, Joy Van Nostrand, Mary K F, Zhou J Z 2022 Proc. Natl. Acad. Sci. USA 119 e2109995119
Google Scholar
[19] Yu D C, Ulrich P 2010 Phys. Rev. E 82 026108
Google Scholar
[20] Elad S, Michael B II, Ronen S, William B 2006 Nature 440 1007
Google Scholar
[21] Timothy S G, DI Diego B, David L, James J C 2003 Science 301 102
Google Scholar
[22] Barzel, Baruch, Barabási, Albert-László 2013 Nat. Biotechnol. 31 720
Google Scholar
[23] Björn S, Matthias W, Rainer D, Jürgen K, Jens T 2006 Phys. Rev. Lett. 96 208103
Google Scholar
[24] Soheil F, Daniel M, Muriel M, Manolis K 2013 Nat. Biotechnol. 31 726
Google Scholar
[25] Bergner A, Frasca M, Sciuto G, Buscarino A, Ngamga E J, Fortuna L, Kurths J 2012 Phys. Rev. E 85 026208
Google Scholar
[26] Vlasov V, Bifone A 2017 Sci. Rep. 7 10403
Google Scholar
[27] Choudhary A, Saha A, Krueger S, Finke C, Rosa E, Freund J A, Feudel U 2021 Phys. Rev. Res. 3 023144
Google Scholar
[28] Daniel M A, Steven H S 2006 Int. J. Bifurcat. Chaos 16 21
Google Scholar
[29] Karakaya B, Minati L, Gambuzza L V, Frasca M 2019 Phys. Rev. E 99 052301
Google Scholar
[30] Vincenzo N, Miguel V, Mario C, Albert D G, Vito L 2013 Phys. Rev. Lett. 110 174102
Google Scholar
[31] 李江, 刘影, 王伟, 周涛 2024 73 048901
Google Scholar
Li J, Liu Y, Wang W, Zhou T 2024 Acta Phys. Sin. 73 048901
Google Scholar
[32] Tang Y, Shi D H, Lü L Y 2022 Commun. Phys. 5 96
Google Scholar
[33] Dummit D S, Foote R M 2004 Abstract Algebra (Hoboken: John Wiley & Sons) pp106−111
-
图 1 无向单纯复形高阶交互作用的结构模体. 分别表示1阶、2阶和3阶单纯复形. 本文研究2阶单纯形, 描述三个节点之间的相互作用
Fig. 1. Network motifs of undirected simplex structures, including 1-simplex, 2-simplex, and 3-simplex. The case of 2-simplex capturing interactions between three nodes is the focus of the present study.
图 2 基于KS同步过程的网络结构重建步骤. 其中蓝色线表示1阶单纯复形, 蓝色区域、橙黄色区域、红色区域分别表示2阶、3阶、4阶单纯复形
Fig. 2. Framework of network structure reconstruction by synchronization process of KS oscillators. Blue line represents 1-simplex. Blue, orange, red areas represent 2-simplex, 3-simplex and 4-simplex respectively.
图 3 $N=3$的网络中各对节点相位差的时间序列 (a)全连; (b)链式网络. 参数设置: $\omega=0$, $\lambda=1$, $\alpha=0.1$
Fig. 3. Phase difference in a network of $N= 3$: (a) Fully connected; (b) chain connected nodes. Parameters: $\omega=0$, $\lambda=1$, $\alpha=0.1$.
图 4 (a)$N=12$的网络, 其中节点11和节点12随机连入一个全连网络; (b)节点11和节点12的相位差$|\theta_{11}-\theta_{12}|$的时间片段; (c)$N=5$的星形网络, 节点1为中心节点, 其余为叶子节点; (d)星形网络中心与叶子节点的相位差. 所有叶子节点间的相位差为0, 而中心与叶子节点之间存在恒定的非零相位差. 参数设置: $\omega=0$, $\lambda=1$, $\alpha=0.1$
Fig. 4. (a) A network of $N= 12$ nodes with node 11 and node 12 being randomly connected to the fully connected network; (b) temporal segment of the phase difference $|\theta_{10} - \theta_{11} |$ between node 10 and node 11; (c) a star network with one hub node and four leaf nodes; (d) phase difference between leaf nodes are zeros, while non-zero values between the hub and leaf nodes. Parameter values: $\omega=0$, $\lambda=1$, $\alpha=0.1$.
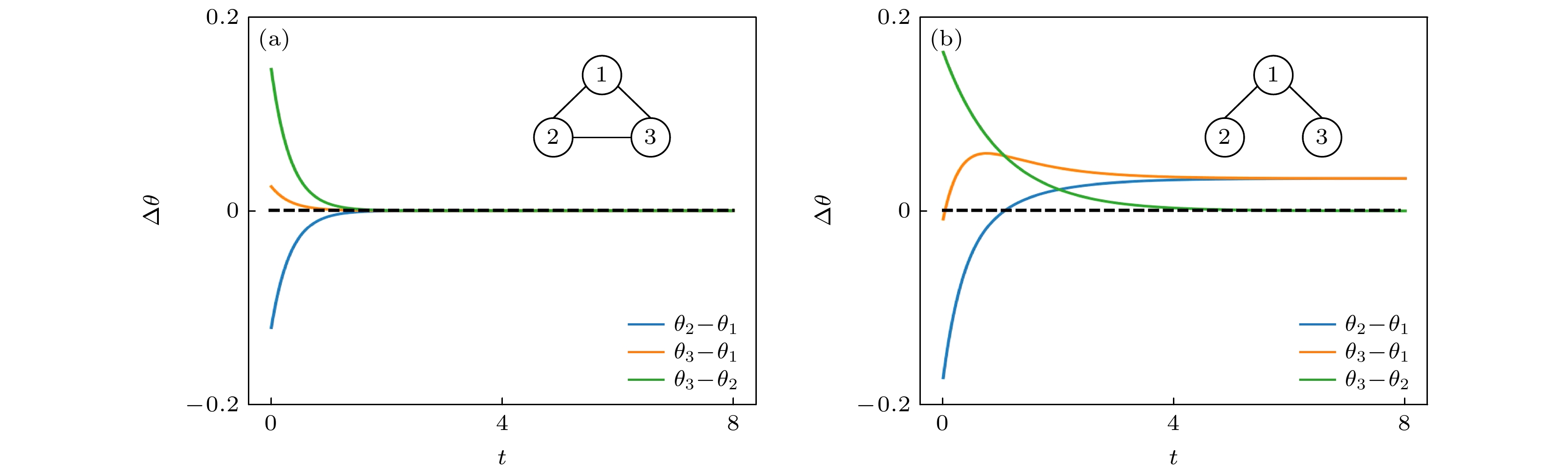
图 5 三个节点组成的链式网络(左下角为网络结构示意图)中相位差的时间序列. 其中黑色虚线为方程(31)的理论解, 蓝色(橙色、绿色)点线分别对应节点1和2 (节点1和3、节点2和3)的相位差$\theta_{12}$($\theta_{13}$, $\theta_{23}$)
Fig. 5. Phase difference of each pair of nodes in a chain of three oscillators (inset shows the schematic network structure). The black dashed line is the theoretical solution by Eq. (31). The blue (orange, green) dot line corresponds to the phase difference between node 1 and node 2 (node 1 and node 3, node 2 and node 3) $\theta_{12}$ ($\theta_{13}$, $\theta_{23}$).
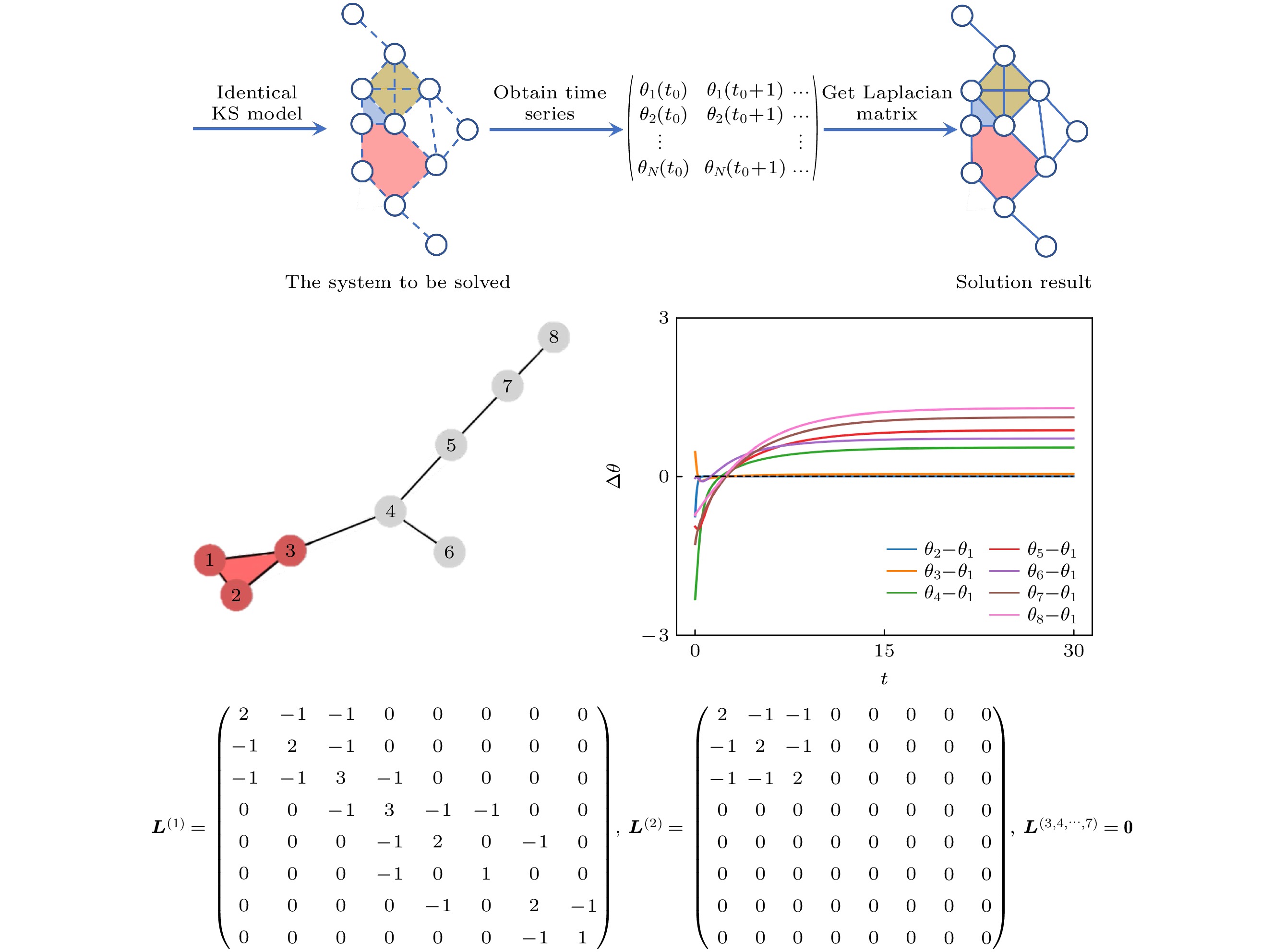
图 6 (a) 由8个节点组成的网络结构示意图, 其中包含了一个二阶单纯复形(由节点1, 2, 3组成)和8个一阶单纯复形; (b) 节点2—8与节点1之间的相位差, 其中仅有$\theta_1-\theta_2$的相位差值快速收敛至稳态值0
Fig. 6. (a) A network consisting of 8 nodes, including one second-order simplex (consisting of nodes 1, 2, 3) and eight first-order simplex; (b) the pairwise phase mismatch between nodes 2−8 and node 1 in the system, where only the phase difference $\theta_1-\theta_2$ converges to 0.
-
[1] Réka A, Albert-László B 2002 Rev. Mod. Phys. 74 47
Google Scholar
[2] Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D U 2006 Phys. Rep. 424 175
Google Scholar
[3] Federico B, Giulia C, Iacopo I, Vito L, Maxime L, Alice P, Jean-Gabriel Y Giovanni P 2020 Phys. Rep. 874 1
Google Scholar
[4] Hidetsugu S, Yoshiki K 1986 Prog. Theor. Phys. 76 576
Google Scholar
[5] Shinya W, Steven H S 1993 Phys. Rev. Lett. 70 2391
Google Scholar
[6] 张海峰, 王文旭 2020 69 088906
Google Scholar
Zhang H F, Wang W X 2020 Acta Phys. Sin. 69 088906
Google Scholar
[7] Wang W, Nie Y Y, Li W Y, Lin T, Shang M S, Su S, Tang Y, Zhang Y C 2024 Phys. Rep. 1056 1
Google Scholar
[8] Andrea F, Salvatore C, Giulio R 2023 App. Net. Sci. 8 31
Google Scholar
[9] Eyal Bairey, Eric D K, Roy K 2016 Nat. Commun. 7 12285
Google Scholar
[10] Nian F Z, Shi Y Y, Cao J 2021 J Comput. Sci.-Neth. 55 101438
Google Scholar
[11] Alessia A, Gennaro C, Vittorio S, Carmine S 2021 IEEE Access 9 140938
Google Scholar
[12] Marc T, Jose C 2014 J. Phys. A 47 343001
Google Scholar
[13] Marc T 2007 Phys. Rev. Lett. 98 224101
Google Scholar
[14] Yu D C, Marco R, Ljupco K 2006 Phys. Rev. Lett. 97 188701
Google Scholar
[15] Wang W X, Yang R, Lai Y C, Vassilios K, Celso G 2011 Phys. Rev. Lett. 106 154101
Google Scholar
[16] 徐翔, 朱承, 朱先强 2021 70 088901
Google Scholar
Xu X, Zhu C, Zhu X Q 2021 Acta Phys. Sin. 70 088901
Google Scholar
[17] Jose C, Mor N, Sarah H, Marc T 2017 Nat. Commun. 8 2192
Google Scholar
[18] Xiao N J, Zhou A F, Megan L. Kempher, Jason Z. Shi, Yuan M T, Guo X, Wu L W, Ning D L, Joy Van Nostrand, Mary K F, Zhou J Z 2022 Proc. Natl. Acad. Sci. USA 119 e2109995119
Google Scholar
[19] Yu D C, Ulrich P 2010 Phys. Rev. E 82 026108
Google Scholar
[20] Elad S, Michael B II, Ronen S, William B 2006 Nature 440 1007
Google Scholar
[21] Timothy S G, DI Diego B, David L, James J C 2003 Science 301 102
Google Scholar
[22] Barzel, Baruch, Barabási, Albert-László 2013 Nat. Biotechnol. 31 720
Google Scholar
[23] Björn S, Matthias W, Rainer D, Jürgen K, Jens T 2006 Phys. Rev. Lett. 96 208103
Google Scholar
[24] Soheil F, Daniel M, Muriel M, Manolis K 2013 Nat. Biotechnol. 31 726
Google Scholar
[25] Bergner A, Frasca M, Sciuto G, Buscarino A, Ngamga E J, Fortuna L, Kurths J 2012 Phys. Rev. E 85 026208
Google Scholar
[26] Vlasov V, Bifone A 2017 Sci. Rep. 7 10403
Google Scholar
[27] Choudhary A, Saha A, Krueger S, Finke C, Rosa E, Freund J A, Feudel U 2021 Phys. Rev. Res. 3 023144
Google Scholar
[28] Daniel M A, Steven H S 2006 Int. J. Bifurcat. Chaos 16 21
Google Scholar
[29] Karakaya B, Minati L, Gambuzza L V, Frasca M 2019 Phys. Rev. E 99 052301
Google Scholar
[30] Vincenzo N, Miguel V, Mario C, Albert D G, Vito L 2013 Phys. Rev. Lett. 110 174102
Google Scholar
[31] 李江, 刘影, 王伟, 周涛 2024 73 048901
Google Scholar
Li J, Liu Y, Wang W, Zhou T 2024 Acta Phys. Sin. 73 048901
Google Scholar
[32] Tang Y, Shi D H, Lü L Y 2022 Commun. Phys. 5 96
Google Scholar
[33] Dummit D S, Foote R M 2004 Abstract Algebra (Hoboken: John Wiley & Sons) pp106−111
下载:
计量
- 文章访问数: 1520
- PDF下载量: 86
- 被引次数: 0
