-
针对目前亥姆霍兹共振器的低频吸声效果不理想的问题, 提出了一种粗糙颈管亥姆霍兹共振器吸声体, 将粗糙度引入亥姆霍兹共振器的颈管, 改变经典亥姆霍兹共振器颈管形状并构建粗糙颈管亥姆霍兹共振器吸声体结构, 可以在不改变整体尺寸的前提下, 有效地为吸声器提供低频吸声所需的声阻抗, 从而降低共振频率. 利用有限元法对结构进行了仿真并通过阻抗管吸声测试进行验证, 实验与仿真具有较高的一致性. 基于以上验证, 颈管引入粗糙度后可以有效降低亥姆霍兹共振器吸收峰值频率, 设计了8个吸声单元紧凑组合的粗糙颈管低频宽带通风消声器. 相比于光滑颈管的消声器, 吸声效果由500—1100 Hz频段内0.8以上的宽频吸声优化为400—1200 Hz频段内0.8以上的吸声效果, 可为低频宽带通风消声器的设计与优化提供参考.Aiming at the unsatisfactory low-frequency sound absorption effect of Helmholtz resonator, a novel broadband low-frequency ventilation absorber with rough neck is proposed. The roughness is introduced into the neck of Helmholtz resonator to change the shape of the neck and achieve the structure of rough neck Helmholtz resonator. The proposed absorber can effectively provide the acoustic impedance required for low-frequency sound absorption without changing the overall size, thereby reducing the resonant frequency. The finite element method is used to simulate the structure, and the impedance tube sound absorption test is carried out to verify it. The experimental and simulation results show high consistency with each other. The results also indicate that the rough neck Helmholtz resonator absorber with roughness introduced in the neck achieves an absorption peak at 58 Hz, with an absorption coefficient of about 0.63. Comparing with the absorber without roughness introduced, the resonant peak frequency becomes low, from 70 Hz to 58 Hz, reducing 17.1%. Therefore, adjusting the neck roughness can serve as a method of tuning the acoustic performance, and the absorption peak frequency can be adjusted by appropriately increasing the neck roughness so as to move it in the low frequency direction. Based on the verification that the roughness of the neck can effectively reduce the absorption peak frequency of Helmholtz resonator, a broadband low-frequency ventilation absorber with a rough neck, which is composed of eight absorption units, is designed. Through simulation calculation and experimental exploration, the absorption coefficient can achieve more than 0.8 in a target working frequency band of 500－1100 Hz. On this basis, the acoustic impedance of the structure can be adjusted by introducing roughness into the neck of Helmholtz resonator, so as to obtain the optimized broadband low-frequency ventilation absorber with a rough neck, which achieves a broadband sound absorption coefficient higher than 0.8 in a frequency range of 400–1200 Hz. The optimized structure also has 8 consecutive absorption peaks with amplitudes above 0.95. The proposed low-frequency broadband ventilation absorber provides a reference for designing and optimizing efficient low-frequency subwavelength acoustic absorbers. It has a wide range of applications in pipeline noise control.
[1] 马大猷 1993 物理 22 8
Ma D Y 1993 Physics 22 8
[2] 马大猷 2002 声学技术 1 2
Google Scholar
Ma D Y 2002 Tech. Acoust. 1 2
Google Scholar
[3] 王正敏, 饶伟, 李德玉 2019 声学学报 44 834
Google Scholar
Wang Z M, Rao W, Li D Y 2019 Acta Acust. 44 834
Google Scholar
[4] 刘海涛, 郑四发, 连小珉, 但佳壁 2014 声学学报 39 353
Google Scholar
Liu H T, Zheng S F, Lian X M, Dan J B 2014 Acta Acust. 39 353
Google Scholar
[5] Bai C G, Wu F M, Wang J J, Jiang J X, Yang B 2022 J. Vib. Control. 29 2
[6] 苏胜利, 张苗, 曹为午 2014 舰船科学技术 36 128
Google Scholar
Su S L, Zhang M, Cao W W 2014 Ship Sci. Technol. 36 128
Google Scholar
[7] Romero-García V, Theocharis O, Merkel A, Tournat V, Pagneux V 2016 Sci. Rep. 6 1
Google Scholar
[8] Jiménez N, Huang W, Romero-García V, Pagneux V, Groby J P 2016 Appl. Phys. Lett. 109 121902
Google Scholar
[9] Duan M Y, Yu C L, Xu Z M, Xin F X, Lu T J 2020 Appl. Phys. Lett. 117 151904
Google Scholar
[10] Nguyen H, Wu Q, Xu X, Chen H, Tracy Sharon, Huang G L 2020 Appl. Phys. Lett. 117 134103
Google Scholar
[11] Mao Q B, Li S Q, Liu W W 2018 Appl. Acoust. 141 348
Google Scholar
[12] Duan H Q, Shen X M, Wang Y S, Yang F, Zhang X N, Yin Q 2021 Appl. Phys. Lett. 118 241904
Google Scholar
[13] Zhang L, Xin F X 2022 J. Acoust. Soc. Am. 151 1191
Google Scholar
[14] Liu G S, Peng Y Y, Liu M H, Zou X Y, Cheng J C 2018 Appl. Phys. Lett. 113 153503
Google Scholar
[15] Duan M Y, Yu C L, Xin F X, Lu T J 2021 Appl. Phys. Lett. 118 071904
Google Scholar
[16] Chang H T, Liu L, Zhang C, Xu X H 2018 AIP Adv. 8 045115
Google Scholar
[17] Yang D, Wang X L, Zhu M 2014 J. Sound Vib. 333 6843
Google Scholar
[18] Huang S B, Fang X S, Wang X S, Assouar Badreddine, Cheng Q, Li Y 2019 J. Acoust. Soc. Am. 145 254
Google Scholar
[19] Guo J W, Zhang X, Fang Y, Jiang Z Y 2020 Appl. Phys. Lett. 117 221902
Google Scholar
[20] Duan M Y, Yu C L, Xin F X, Lu T J 2021 J. Appl. Phys. 130 135102
Google Scholar
[21] Song S Y, Yang X H, Xin F X, Lu T J 2018 Phys. Fluids 30 023604
Google Scholar
[22] Xu Z M, Peng X J, Liu X W, Xin F X, Lu T J 2019 EPL 125 34004
Google Scholar
[23] Pride S R, Morgan F D, Gangi A F 1993 Phys. Rev. B 47 4964
Google Scholar
[24] Long H, Cheng Y, Liu X 2018 Sci. Rep. 8 15678
Google Scholar
[25] Hong Z H, Wu F M, Bai C G, An K X, Wang J J, Yang B 2022 Appl. Acoust. 192 108730
Google Scholar
-
图 1 (a) 粗糙直管与光滑直管对比; (b) 直角坐标系下两种直管结构对比; (c) 光滑颈管亥姆霍兹共振器吸声体结构; (d) 粗糙弯曲管与光滑弯曲管结构对比; (e) 极坐标系下两种弯曲管内壁曲线函数; (f) 粗糙颈管亥姆霍兹共振器吸声体结构
Fig. 1. (a) Comparison of rough and smooth straight pipes; (b) comparison of two kinds of straight pipe structures in cartesian coordinate system; (c) sound absorber structure of smooth neck Helmholtz resonator; (d) comparison of rough-curved and smooth-curved tubes; (e) curve function of two kinds of bending tube inwall in polar coordinate system; (f) sound absorber structure of rough neck Helmholtz resonator.
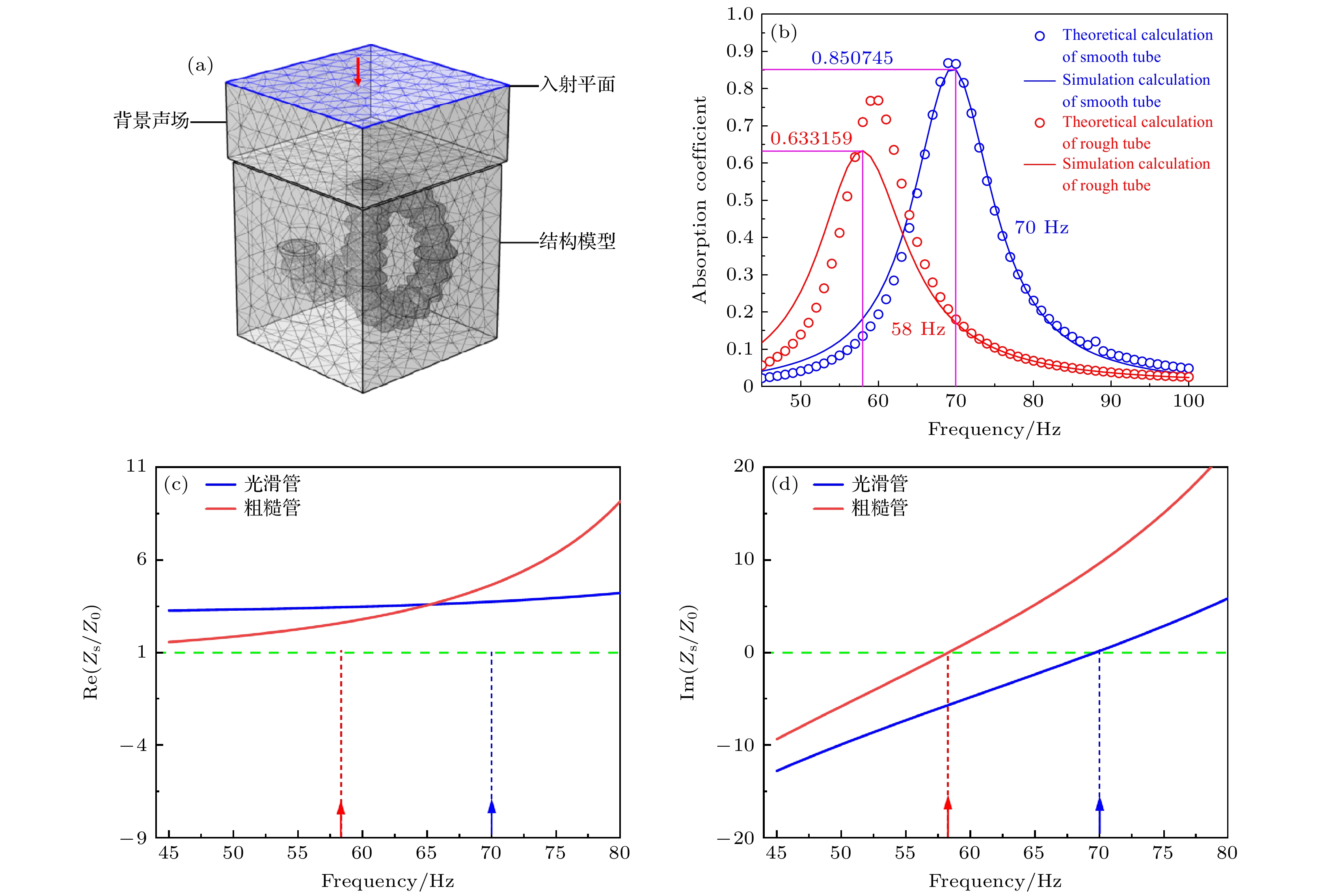
图 2 结构有限元仿真 (a) 有限元网格划分模型; (b) 两种结构理论及仿真吸声曲线对比; (c) 两种结构相对阻抗实部对比; (d) 两种结构相对阻抗实部对比
Fig. 2. Finite element simulation of structures: (a) Finite element meshing model; (b) comparison of two structural theories and simulation sound absorption curves; (c) comparison of the relative impedance realities of the two structures; (d) comparison of the relative impedance imaginary parts of the two structures.
图 3 粗糙颈管亥姆霍兹共振器吸声体吸声机理 (a) 粗糙颈管的声能耗散密度; (b)粗糙颈管的粒子振动速度分布; (c)光滑颈管的声能耗散密度; (d)光滑颈管的粒子振动速度分布
Fig. 3. Sound absorption mechanism of Helmholtz resonator sound-absorber in rough neck tube: (a) Distribution of particle vibration velocity in smooth neck canal; (b) distribution of particle vibration velocity in rough neck canals; (c) acoustic energy dissipation density of smooth neck tubes; (d) acoustic dissipation density of the rough neck tube.
图 4 粗糙度对吸声性能的影响 (a)不同轴向粗糙度下的吸收谱; (b)不同径向粗糙度下的吸收谱
Fig. 4. Effect of roughness on sound absorption performance: (a) Absorption spectra at different axial roughness; (b) absorption spectra at different radial roughness.
图 5 (a) LBVA单元的二维示意图; (b) R-LBVA单元的二维示意图
Fig. 5. (a) 2D schematic diagram of LBVA cell; (b) 2D schematic diagram of R-LBVA cell.
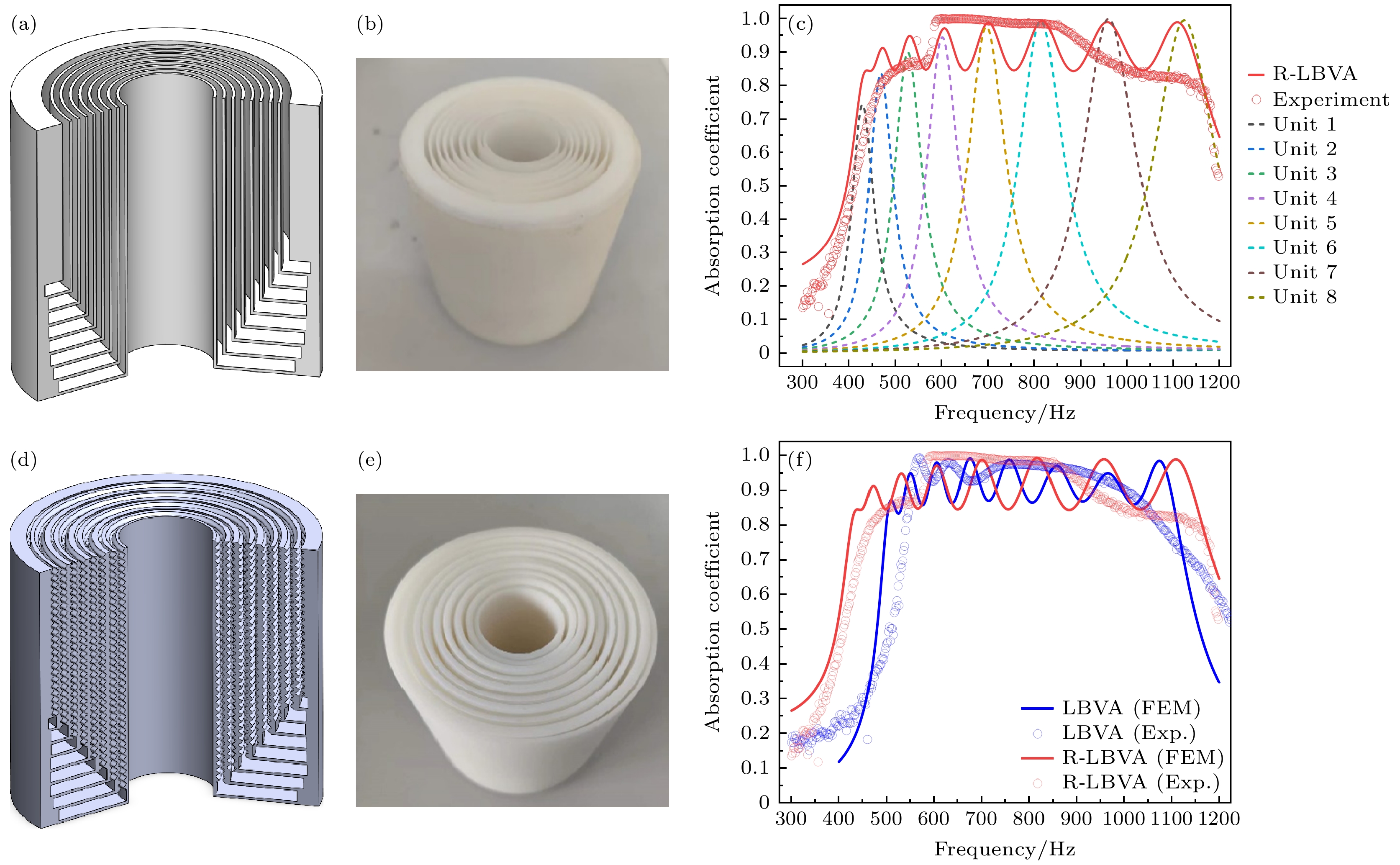
图 6 结构及结果 (a) LBVA三维截面视图; (b) LBVA-3D打印结构图; (c) 有限元仿真及阻抗管测试所得R-LBVA和各个吸声单元的吸声曲线; (d) R-LBVA三维截面视图; (e) R-LBVA-3D打印结构图; (f)有限元仿真及阻抗管测试所得LBVA和R-LBVA的吸声曲线
Fig. 6. Structure and results: (a) LBVA 3D section view; (b) LBVA-3D printing structure diagram; (c) R-LBVA and absorption curves of each absorption unit obtained by finite element simulation and impedance tube measurement; (d) R-LBVA 3D section view; (e) R-LBVA-3D printing structure diagram; (f) LBVA and R-LBVA obtained by finite element simulation and impedance tube measurement.
图 7 (a) R-LBVA各峰值频率下的相对声压分布; (b) 1109 Hz处R-LBVA第8个吸声单元颈部的粒子振动速度分布; (c) 1109 Hz处R-LBVA第8个吸声单元颈部的声能耗散密度分布; (d) R-LBVA的相对阻抗虚部; (e) R-LBVA的相对阻抗实部
Fig. 7. (a) Relative sound pressure distribution at each peak frequency of R-LBVA; (b) particle vibration velocity distribution at the neck of R-LBVA sound absorption unit 8 at 1109 Hz; (c) sound energy dissipation density distribution at the neck of R-LBVA sound absorption unit 8 at 1109 Hz; (d) imaginary part of relative impedance of R-LBVA; (e) real part of relative impedance of R-LBVA.
表 1 LBVA单元的几何参数(单位: mm)
Table 1. Geometric parameters of R-LBVA units (in: mm).
Unit1 Unit2 Unit3 Unit4 Unit5 Unit6 Unit7 Unit8 d 2 2 2 2 2 2 2 2 Rc 16 20.5 23.5 26.5 28 31 35.5 38.5 h 4 4 4 4 4 4 4 4 w 26.3 24 22.2 19 17.5 14.1 9.8 7.7 l 90 85 80 75 70 65 60 55 d 5 5 5 5 5 5 5 5 δ 1 1 1 1 1 1 1 1 
下载: 导出CSV
-
[1] 马大猷 1993 物理 22 8
Ma D Y 1993 Physics 22 8
[2] 马大猷 2002 声学技术 1 2
Google Scholar
Ma D Y 2002 Tech. Acoust. 1 2
Google Scholar
[3] 王正敏, 饶伟, 李德玉 2019 声学学报 44 834
Google Scholar
Wang Z M, Rao W, Li D Y 2019 Acta Acust. 44 834
Google Scholar
[4] 刘海涛, 郑四发, 连小珉, 但佳壁 2014 声学学报 39 353
Google Scholar
Liu H T, Zheng S F, Lian X M, Dan J B 2014 Acta Acust. 39 353
Google Scholar
[5] Bai C G, Wu F M, Wang J J, Jiang J X, Yang B 2022 J. Vib. Control. 29 2
[6] 苏胜利, 张苗, 曹为午 2014 舰船科学技术 36 128
Google Scholar
Su S L, Zhang M, Cao W W 2014 Ship Sci. Technol. 36 128
Google Scholar
[7] Romero-García V, Theocharis O, Merkel A, Tournat V, Pagneux V 2016 Sci. Rep. 6 1
Google Scholar
[8] Jiménez N, Huang W, Romero-García V, Pagneux V, Groby J P 2016 Appl. Phys. Lett. 109 121902
Google Scholar
[9] Duan M Y, Yu C L, Xu Z M, Xin F X, Lu T J 2020 Appl. Phys. Lett. 117 151904
Google Scholar
[10] Nguyen H, Wu Q, Xu X, Chen H, Tracy Sharon, Huang G L 2020 Appl. Phys. Lett. 117 134103
Google Scholar
[11] Mao Q B, Li S Q, Liu W W 2018 Appl. Acoust. 141 348
Google Scholar
[12] Duan H Q, Shen X M, Wang Y S, Yang F, Zhang X N, Yin Q 2021 Appl. Phys. Lett. 118 241904
Google Scholar
[13] Zhang L, Xin F X 2022 J. Acoust. Soc. Am. 151 1191
Google Scholar
[14] Liu G S, Peng Y Y, Liu M H, Zou X Y, Cheng J C 2018 Appl. Phys. Lett. 113 153503
Google Scholar
[15] Duan M Y, Yu C L, Xin F X, Lu T J 2021 Appl. Phys. Lett. 118 071904
Google Scholar
[16] Chang H T, Liu L, Zhang C, Xu X H 2018 AIP Adv. 8 045115
Google Scholar
[17] Yang D, Wang X L, Zhu M 2014 J. Sound Vib. 333 6843
Google Scholar
[18] Huang S B, Fang X S, Wang X S, Assouar Badreddine, Cheng Q, Li Y 2019 J. Acoust. Soc. Am. 145 254
Google Scholar
[19] Guo J W, Zhang X, Fang Y, Jiang Z Y 2020 Appl. Phys. Lett. 117 221902
Google Scholar
[20] Duan M Y, Yu C L, Xin F X, Lu T J 2021 J. Appl. Phys. 130 135102
Google Scholar
[21] Song S Y, Yang X H, Xin F X, Lu T J 2018 Phys. Fluids 30 023604
Google Scholar
[22] Xu Z M, Peng X J, Liu X W, Xin F X, Lu T J 2019 EPL 125 34004
Google Scholar
[23] Pride S R, Morgan F D, Gangi A F 1993 Phys. Rev. B 47 4964
Google Scholar
[24] Long H, Cheng Y, Liu X 2018 Sci. Rep. 8 15678
Google Scholar
[25] Hong Z H, Wu F M, Bai C G, An K X, Wang J J, Yang B 2022 Appl. Acoust. 192 108730
Google Scholar
下载:
计量
- 文章访问数: 3821
- PDF下载量: 88
- 被引次数: 0
