-
通过求解Bogoliubov-de Gennes方程研究一维S/FL-F-FR/S结中Josephson电流的输运特性, 其中S和F分别是超导体和铁磁体, FL,R是左右两侧具有非共线磁矩的界面层. 研究发现, FL和FR界面能够产生自旋混合和自旋翻转效应, 该效应能够将S内一部分自旋单重对转化为F内自旋相同的三重对. 对于短S/FL-F-FR/S结, F层内同时存在自旋单重对和自旋相同的三重对. 于是, 随着铁磁交换场和界面磁矩偏转角度差的增加, 临界电流在一个基准面上振荡. 若F转变为半金属, 则F内仅剩自旋相同的三重对, 临界电流的振荡特征消失. 此外, FL和FR界面还能起到普通势垒的作用. 这将导致临界电流随着铁磁厚度的增加展现出双重振荡行为, 其中长波振荡源于铁磁体内自旋单重对的位相变化, 短波振荡是由自旋单重对和自旋相同的三重对经过两个界面势垒时的共振隧穿效应引起的.
-
关键词:
- Josephson结 /
- 铁磁体 /
- 自旋三重对 /
- 共振隧穿
Based on the Bogoliubov-de Gennes equations, we investigate the transport of the Josephson current in a one-dimensional S/FL-F-FR/S junction, where S and F are superconductor and ferromagnet, and FL,R are the left and right interfaces with noncollinear magnetizations. It is found that the FL and FR interfaces can induce spin-mixing and spin-flip effects, which can transform a part of spin-singlet pairs in the S into equal-spin triplet pairs in the F. For the short S/FL-F-FR/S junction, the spin-singlet pairs and the equal-spin triplet pairs can survive in the F layer. Therefore, with the increase of the ferromagnetic exchange field and the angle difference of interface magnetization rotation, the critical current oscillates on a base level. If the F is transformed into half-metal, only the equal-spin triple pairs exist in the F layer, and the oscillation characteristic of critical current disappears. In addition, the FL and FR interfaces can work as conventional potential barriers. As a result, the critical current exhibits double oscillation behaviors with the increase of ferromagnetic thickness, in which the long-wave oscillation arises from the phase change of the spin-singlet pairs in the ferromagnetic layer, and the short-wave oscillation is caused by the resonant tunneling effect when the spin-singlet pairs and the equal-spin triplet pairs pass through two interfacial barriers.-
Keywords:
- Josephson junction /
- ferromagnet /
- spin-triplet pair /
- resonant tunneling
[1] Golubov A A, Kupriyanov M Y, Il’ichev E 2004 Rev. Mod. Phys. 76 411
Google Scholar
[2] Buzdin A I 2005 Rev. Mod. Phys. 77 935
Google Scholar
[3] Bergeret F S, Volkov A F, Efetov K B 2005 Rev. Mod. Phys. 77 1321
Google Scholar
[4] Eschrig M 2011 Phys. Today 64 43
Google Scholar
[5] Blamire M G, Robinson J W A 2014 J. Phys. Condens. Matter 26 453201
Google Scholar
[6] Linder J, Robinson J W A 2015 Nat. Phys. 11 307
Google Scholar
[7] Eschrig M 2015 Rep. Prog. Phys. 78 104501
Google Scholar
[8] Mel'nikov A S, Mironov S V, Samokhvalov A V, Buzdin A I 2022 Physics-Uspekhi 65 1248
Google Scholar
[9] Kimura T, Otani Y, Hamrle J 2006 Phys. Rev. Lett. 96 037201
Google Scholar
[10] Keizer R S, Goennenwein S T B, Klapwijk T M, Miao G, Xiao G, Gupta A 2006 Nature 439 825
Google Scholar
[11] Anwar M S, Czeschka F, Hesselberth M, Porcu M, Aarts J 2010 Phys. Rev. B 82 100501(R
Google Scholar
[12] Kontos T, Aprili M, Lesueur J, Genêt F, Stephanidis B, Boursier R 2002 Phys. Rev. Lett. 89 137007
Google Scholar
[13] Jiang J S, Davidović D, Reich D H, Chien C L 1995 Phys. Rev. Lett. 74 314
Google Scholar
[14] Blum Y, Tsukernik A, Karpovski M, Palevski A 2002 Phys. Rev. Lett. 89 187004
Google Scholar
[15] Ryazanov V V, Oboznov V A, Rusanov A Yu, Veretennikov A V, Golubov A A, Aarts J 2001 Phys. Rev. Lett. 86 2427
Google Scholar
[16] Oboznov V A, Bol’ginov V V, Feofanov A K, Ryazanov V V, Buzdin A I 2006 Phys. Rev. Lett. 96 197003
Google Scholar
[17] Yamashita T, Takahashi S, Maekawa S 2006 Appl. Phys. Lett. 88 132501
Google Scholar
[18] Bergeret F S, Volkov A F, Efetov K B 2001 Phys. Rev. Lett. 86 4096
Google Scholar
[19] Kadigrobov A, Shekhter R I, Jonson M 2001 Europhys. Lett. 54 394
Google Scholar
[20] Eschrig M, Kopu J, Cuevas J C, Gerd Schön 2003 Phys. Rev. Lett. 90 137003
Google Scholar
[21] Houzet M, Buzdin A I 2007 Phys. Rev. B 76 060504(R
Google Scholar
[22] Asano Y, Tanaka Y, Golubov A A 2007 Phys. Rev. Lett. 98 107002
Google Scholar
[23] Sosnin I, Cho H, Petrashov V T, Volkov A F 2006 Phys. Rev. Lett. 96 157002
Google Scholar
[24] Robinson J W A, Witt J D S, Blamire M G 2010 Science 329 59
Google Scholar
[25] Khaire T S, Khasawneh M A, Pratt W P, Birge N O 2010 Phys. Rev. Lett. 104 137002
Google Scholar
[26] Klose C, Khaire T S, Wang Y X, et al. 2012 Phys. Rev. Lett. 108 127002
Google Scholar
[27] Martinez W M, Pratt W P, Birge N O 2016 Phys. Rev. Lett. 116 077001
Google Scholar
[28] Sanchez-Manzano D, Mesoraca S, Cuellar F A, et al. 2022 Nat. Mater. 21 188
Google Scholar
[29] De Gennes P G 1966 Superconductivity of Metals and Alloys (New York: Benjamin) pp137–170
[30] Bagwell P F 1992 Phys. Rev. B 46 12573
Google Scholar
[31] Beenakker C W J 1991 Phys. Rev. Lett. 67 3836
Google Scholar
[32] Bardeen J, Kümmel R, Jacobs A E, Tewordt L 1969 Phys. Rev. 187 556
Google Scholar
[33] Cayssol J, Montambaux G 2004 Phys. Rev. B 70 224520
Google Scholar
[34] Bulaevskii L N, Buzdin A I, Kulić M L, Panyukov S V 1985 Adv. Phys. 34 175
Google Scholar
[35] Meng H, Wu X Q, Ren Y J, Wu J S 2022 Phys. Rev. B 106 174502
Google Scholar
[36] Markos P, Soukoulis C M 2008 Wave Propagation: From Electrons to Photonic Crystals and Left-Handed Materials (Princeton: Princeton University Press) pp56–73
[37] Cohen-Tannoudji C, Diu B, Laloë F 2019 Quantum Mechanics (Vol. 1) (Weinheim: Wiley-VCH) pp2–32
[38] Iogansen L V 1964 Sov. Phys.-JETP 18 146
[39] Meng H, Wu X Q, Zheng Z M 2013 Europhys. Lett. 104 37003
Google Scholar
[40] Meng H, Wu J S, Wu X Q, Ren M Y, Ren Y J 2016 Sci. Rep. 6 21308
Google Scholar
-
图 1 (a) S/FL-F-FR/S结的结构示意图, 其中F内的粗箭头表示交换场方向, FL和FR为具有非共线磁矩的自旋活性界面; (b) Fj界面处磁矩
$ {{\boldsymbol{\rho}}}_{j} $ 的磁化方向, 其中$ {j}=\rm{L} $ ,$ \rm{R} $ 分别对应左侧和右侧界面.$ \theta_{j} $ 和$ \chi_{j} $ 分别表示Fj界面的极化角和方位角Fig. 1. (a) Schematic diagram of the S/FL-F-FR/S junction, where thick arrow in F indicates the directions of the exchange field, and the FL and FR are spin-active interfaces with non-collinear magnetic moments; (b) the direction of magnetization
$ {{\boldsymbol{\rho}}}_{j} $ at the Fj interface, where$ {j}=\rm{L} $ and$ \rm{R} $ correspond to the left and right interfaces, respectively.$ \theta_{j} $ and$ \chi_{j} $ denote polar and azimuthal angles of the Fj interface, respectively
图 2 S/F/S结中Josephson电流随铁磁特征的变化 (a)临界电流
$ I_{{\rm{c}}} $ 随铁磁交换场$ h_{z} $ 和铁磁厚度d的变化特征; (b)不同交换场下$ I_{{\rm{c}}} $ 随d的变化特征; (c)不同铁磁厚度时$ I_{{\rm{c}}} $ 随$ h_{z} $ 的变化特征;$ h_{z}/E_{{\rm{F}}} = 0.15 $ 时的(d)Andreev能谱$ E_{\rm{A}}(\phi) $ 和(e)电流-位相关系$ I(\phi) $ . 在所有图形中, 界面极化强度取$ P_{{\rm{L}}}=P_{{\rm{R}}} = 0 $ Fig. 2. Variation of Josephson current with ferromagnetic characteristics in the S/F/S junction: (a) Critical current
$ I_{{\rm{c}}} $ versus exchange field$ h_z $ and ferromagnetic thickness d; (b) dependence of$ I_{{\rm{c}}} $ on d for different exchange fields; (c) dependence of$ I_{{\rm{c}}} $ on$ h_z $ for different ferromagnetic thicknesses; (d) Andreev energy spectrum$ E_{\rm{A}}(\phi) $ and (e) current-phase relation$ I(\phi) $ for$ h_{z}/E_{{\rm{F}}} = $ $ 0.15 $ . In all panels, the strengths of interfacial polarization are taken as$ P_{{\rm{L}}}=P_{{\rm{R}}} = 0 $ 
图 3 临界电流
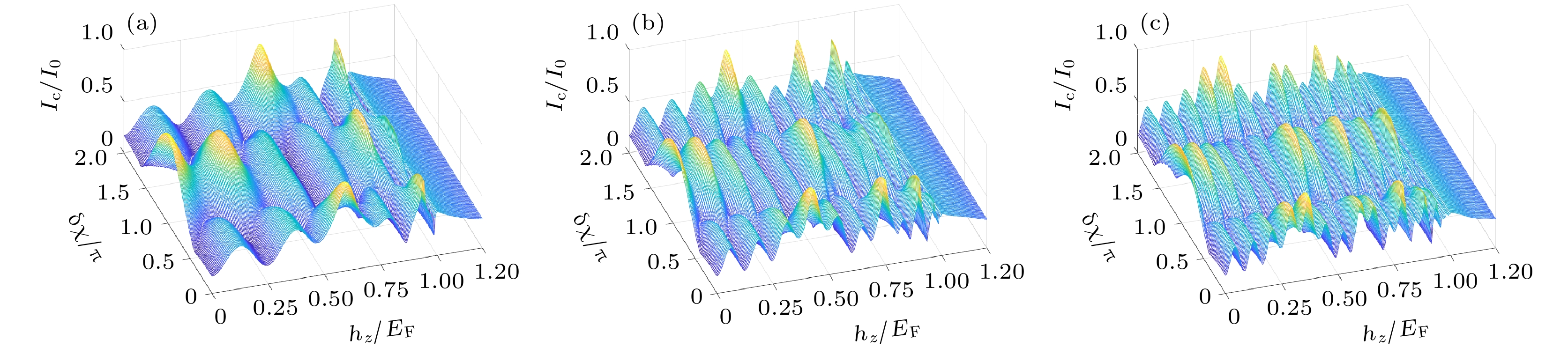
$ I_{\rm{c}} $ 随铁磁交换场$ h_z $ 和界面磁矩偏转角度差$ {\text{δ}}\chi $ 的变化特征 (a) kFd = 25; (b) kFd = 50; (c) kFd = 70. 在所有图形中, 界面极化强度取$ P_{{\rm{L}}}=P_{{\rm{R}}} = 1 $ Fig. 3. The critical current
$ I_{{\rm{c}}} $ versus exchange field$ h_z $ and angle difference of interface magnetization rotation$ {\text{δ}}\chi $ : (a) kFd = 25; (b) kFd = 50; (c) kFd = 70. In all panels, the strengths of interfacial polarization are taken as$ P_{{\rm{L}}}=P_{{\rm{R}}} = 1 $ 
图 4 临界电流
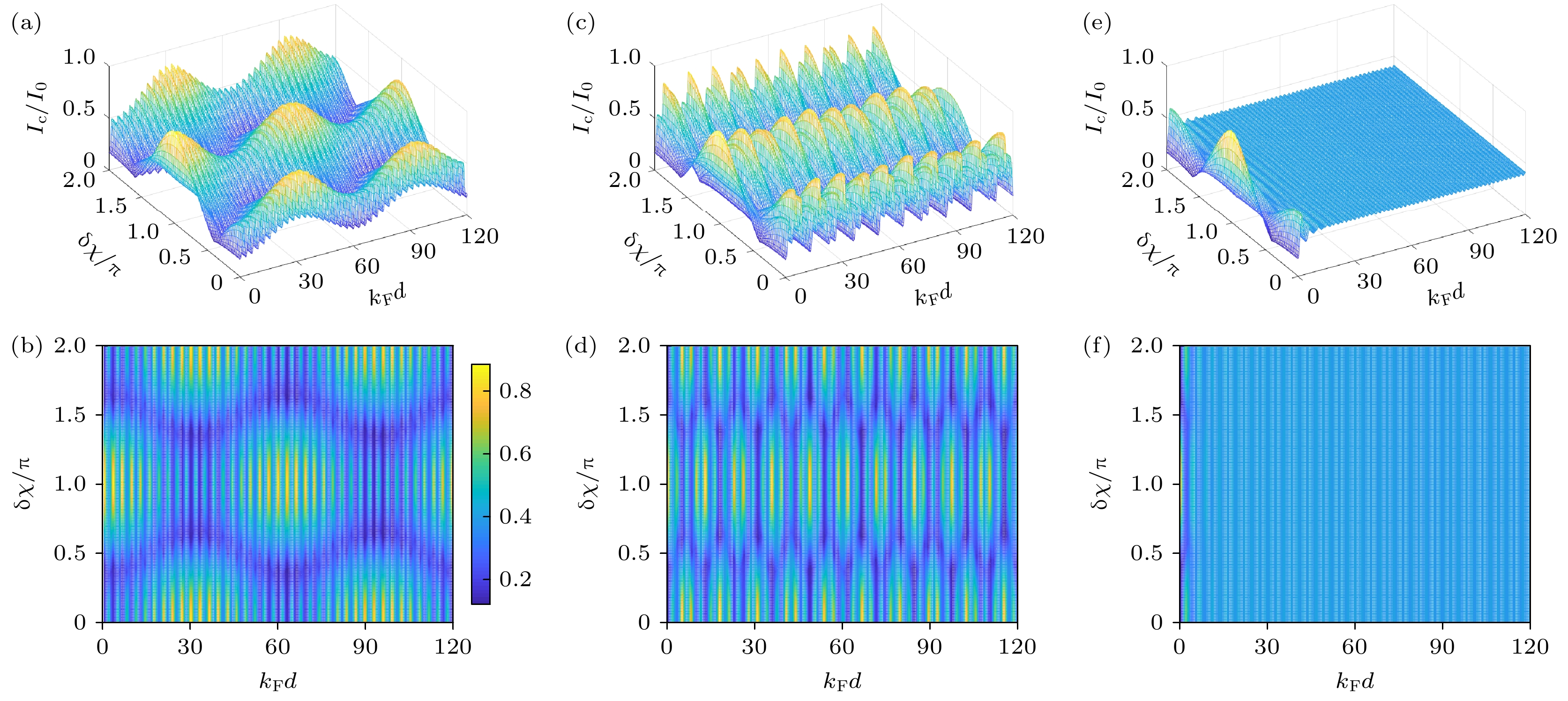
$ I_{\rm{c}} $ 随铁磁层厚度d和界面磁矩偏转角度差$ {\text{δ}}\chi $ 的变化特征 (a), (c), (e) 电流变化的侧视图; (b), (d), (f) 电流变化的俯视图. (a), (b)$ h_z/E_{{\rm{F}}} = 0.1 $ ; (c), (d)$ h_z/E_{{\rm{F}}} = 0.5 $ ; (e), (f)$ h_z/E_{\rm{F}} = 1.01 $ . 在所有图形中, 界面极化强度取$ P_{{\rm{L}}}=P_{{\rm{R}}} = 1 $ Fig. 4. Variation of the critical current with ferromagnetic thickness d and angle difference of interface magnetization rotation
$ {\text{δ}}\chi $ : (a), (c), (e) Side view of current changes; (b), (d), (f) top view of current changes. (a), (b)$ h_z/E_{{\rm{F}}} = 0.1 $ ; (c), (d)$ h_z/E_{{\rm{F}}} = 0.5 $ ; (e), (f)$ h_z/E_{\rm{F}} = 1.01 $ . In all panels, the strengths of interfacial polarization are taken as$ P_{{\rm{L}}}=P_{{\rm{R}}} = 1 $ .
图 5 (a)
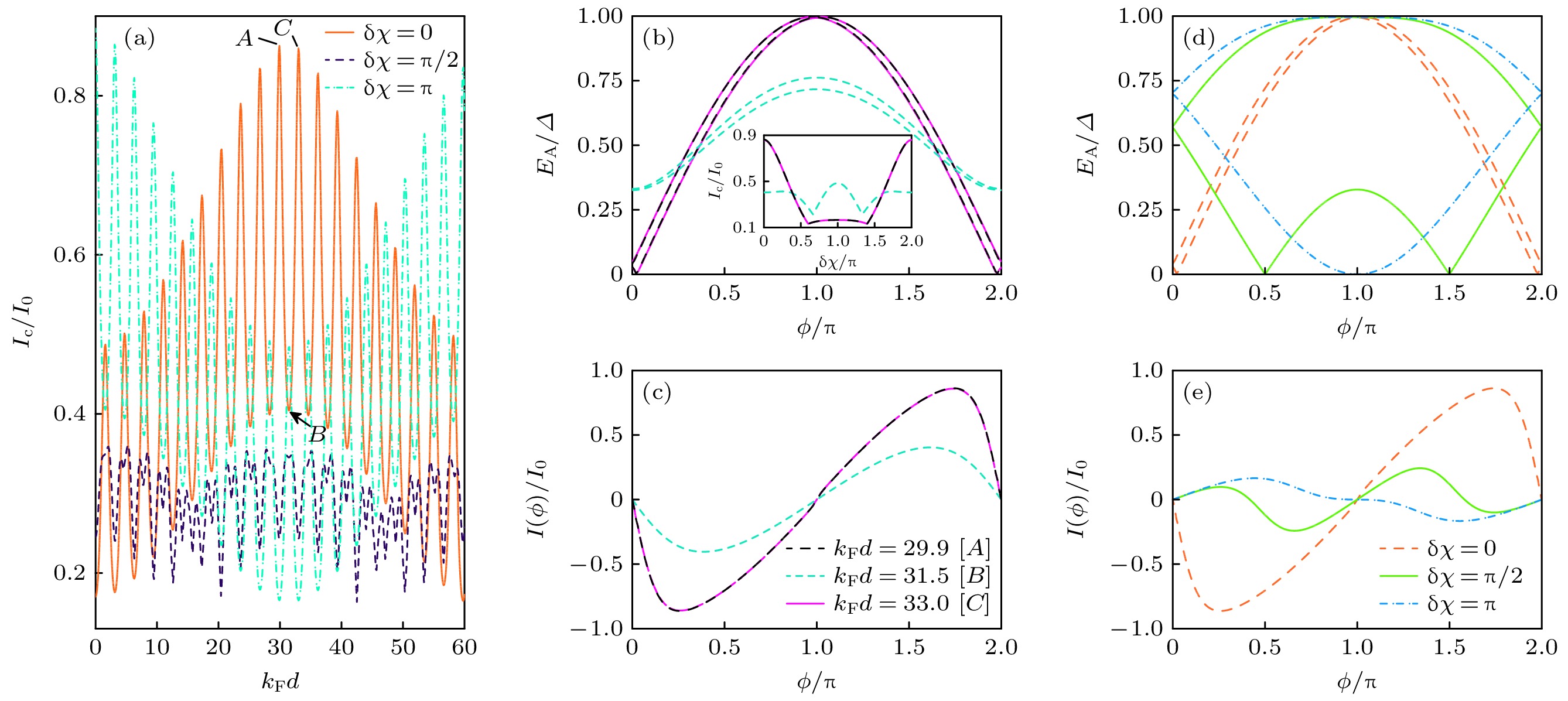
$ {\text{δ}}\chi $ 取3个特殊值时临界电流$ I_{\rm{c}} $ 随铁磁层厚度d的变化特征; (b), (c)$ {\text{δ}}\chi = 0 $ 时的Andreev能谱$ E_{\rm{A}}(\phi)$ 和电流-位相关系$ I(\phi) $ (图(b)插图描述了$ I_{\rm{c }}$ 随$ {\text{δ}}\chi $ 的变化); (d), (e)$ k_{{\rm{F}}}d = 29.9 $ 时的Andreev能谱$ E_{\rm{A}}(\phi) $ 和电流-位相关系$ I(\phi) $ . 在所有图形中, 其他参数为$ h_{z}/E_{{\rm{F}}} = 0.1 $ 和$ P_{{\rm{L}}}=P_{{\rm{R}}} = 1 $ Fig. 5. (a) Variation of the critical current with ferromagnetic thickness d when
$ {\text{δ}}\chi $ takes three special values; (b), (c) Andreev energy spectrum$ E_{\rm{A}}(\phi) $ and current-phase relation$ I(\phi) $ for$ {\text{δ}}\chi = 0 $ (the inset in panel (b) illustrates the dependence of$ I_{\rm{c}} $ on$ {\text{δ}}\chi $ ); (d), (e) Andreev energy spectrum$ E_{\rm{A}}(\phi) $ and current-phase relation$ I(\phi) $ for$ k_{{\rm{F}}}d = 29.9 $ . In all panels, other parameters are$ h_{z}/E_{{\rm{F}}} = 0.1 $ and$ P_{{\rm{L}}}=P_{{\rm{R}}} = 1 $ .
图 6
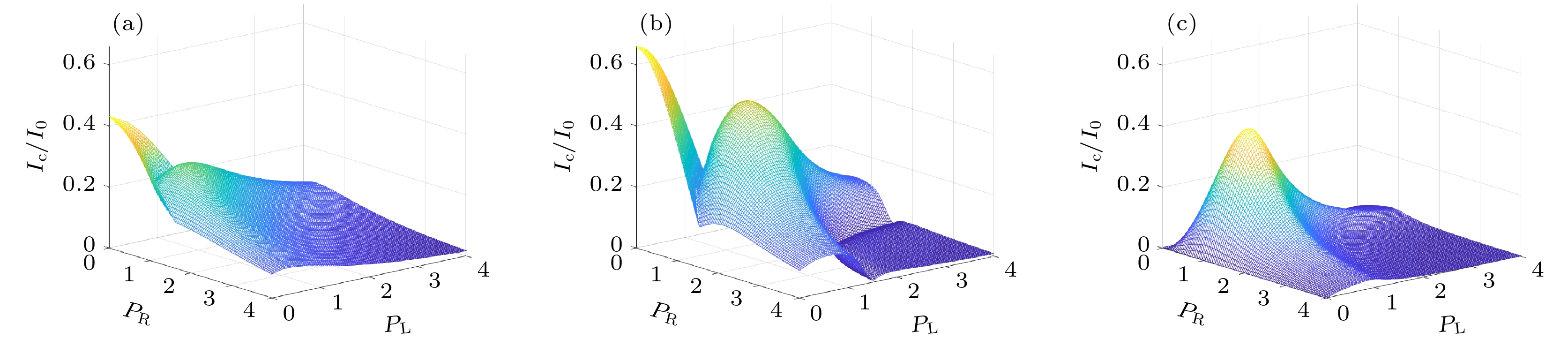
$ {\text{δ}}\chi = 0 $ 时不同铁磁交换场下临界电流$ I_{\rm{c}} $ 随界面极化强度$ P_{{\rm{L}}} $ 和$ P_{{\rm{R}}} $ 的变化特征 (a)$ h_z/E_{{\rm{F}}} $ = 0.1; (b)$ h_z/E_{{\rm{F}}} $ = 0.5; (c)$ h_z/E_{{\rm{F}}} $ = 1.01. 所有图形中, F层厚度取$ k_{{\rm{F}}}d = 50 $ Fig. 6. Variation of the critical current with the strengths of interfacial polarization
$ P_{{\rm{L}}} $ and$ P_{{\rm{R}}} $ for three different exchange fields in the case of$ {\text{δ}}\chi = 0 $ : (a)$ h_z/E_{{\rm{F}}} $ = 0.1; (b)$ h_z/E_{{\rm{F}}} $ = 0.5; (c)$ h_z/E_{{\mathrm{F}}} $ = 1.01. In all panels, the thickness of the F layer is taken as$ k_{{\rm{F}}}d = 50 $ -
[1] Golubov A A, Kupriyanov M Y, Il’ichev E 2004 Rev. Mod. Phys. 76 411
Google Scholar
[2] Buzdin A I 2005 Rev. Mod. Phys. 77 935
Google Scholar
[3] Bergeret F S, Volkov A F, Efetov K B 2005 Rev. Mod. Phys. 77 1321
Google Scholar
[4] Eschrig M 2011 Phys. Today 64 43
Google Scholar
[5] Blamire M G, Robinson J W A 2014 J. Phys. Condens. Matter 26 453201
Google Scholar
[6] Linder J, Robinson J W A 2015 Nat. Phys. 11 307
Google Scholar
[7] Eschrig M 2015 Rep. Prog. Phys. 78 104501
Google Scholar
[8] Mel'nikov A S, Mironov S V, Samokhvalov A V, Buzdin A I 2022 Physics-Uspekhi 65 1248
Google Scholar
[9] Kimura T, Otani Y, Hamrle J 2006 Phys. Rev. Lett. 96 037201
Google Scholar
[10] Keizer R S, Goennenwein S T B, Klapwijk T M, Miao G, Xiao G, Gupta A 2006 Nature 439 825
Google Scholar
[11] Anwar M S, Czeschka F, Hesselberth M, Porcu M, Aarts J 2010 Phys. Rev. B 82 100501(R
Google Scholar
[12] Kontos T, Aprili M, Lesueur J, Genêt F, Stephanidis B, Boursier R 2002 Phys. Rev. Lett. 89 137007
Google Scholar
[13] Jiang J S, Davidović D, Reich D H, Chien C L 1995 Phys. Rev. Lett. 74 314
Google Scholar
[14] Blum Y, Tsukernik A, Karpovski M, Palevski A 2002 Phys. Rev. Lett. 89 187004
Google Scholar
[15] Ryazanov V V, Oboznov V A, Rusanov A Yu, Veretennikov A V, Golubov A A, Aarts J 2001 Phys. Rev. Lett. 86 2427
Google Scholar
[16] Oboznov V A, Bol’ginov V V, Feofanov A K, Ryazanov V V, Buzdin A I 2006 Phys. Rev. Lett. 96 197003
Google Scholar
[17] Yamashita T, Takahashi S, Maekawa S 2006 Appl. Phys. Lett. 88 132501
Google Scholar
[18] Bergeret F S, Volkov A F, Efetov K B 2001 Phys. Rev. Lett. 86 4096
Google Scholar
[19] Kadigrobov A, Shekhter R I, Jonson M 2001 Europhys. Lett. 54 394
Google Scholar
[20] Eschrig M, Kopu J, Cuevas J C, Gerd Schön 2003 Phys. Rev. Lett. 90 137003
Google Scholar
[21] Houzet M, Buzdin A I 2007 Phys. Rev. B 76 060504(R
Google Scholar
[22] Asano Y, Tanaka Y, Golubov A A 2007 Phys. Rev. Lett. 98 107002
Google Scholar
[23] Sosnin I, Cho H, Petrashov V T, Volkov A F 2006 Phys. Rev. Lett. 96 157002
Google Scholar
[24] Robinson J W A, Witt J D S, Blamire M G 2010 Science 329 59
Google Scholar
[25] Khaire T S, Khasawneh M A, Pratt W P, Birge N O 2010 Phys. Rev. Lett. 104 137002
Google Scholar
[26] Klose C, Khaire T S, Wang Y X, et al. 2012 Phys. Rev. Lett. 108 127002
Google Scholar
[27] Martinez W M, Pratt W P, Birge N O 2016 Phys. Rev. Lett. 116 077001
Google Scholar
[28] Sanchez-Manzano D, Mesoraca S, Cuellar F A, et al. 2022 Nat. Mater. 21 188
Google Scholar
[29] De Gennes P G 1966 Superconductivity of Metals and Alloys (New York: Benjamin) pp137–170
[30] Bagwell P F 1992 Phys. Rev. B 46 12573
Google Scholar
[31] Beenakker C W J 1991 Phys. Rev. Lett. 67 3836
Google Scholar
[32] Bardeen J, Kümmel R, Jacobs A E, Tewordt L 1969 Phys. Rev. 187 556
Google Scholar
[33] Cayssol J, Montambaux G 2004 Phys. Rev. B 70 224520
Google Scholar
[34] Bulaevskii L N, Buzdin A I, Kulić M L, Panyukov S V 1985 Adv. Phys. 34 175
Google Scholar
[35] Meng H, Wu X Q, Ren Y J, Wu J S 2022 Phys. Rev. B 106 174502
Google Scholar
[36] Markos P, Soukoulis C M 2008 Wave Propagation: From Electrons to Photonic Crystals and Left-Handed Materials (Princeton: Princeton University Press) pp56–73
[37] Cohen-Tannoudji C, Diu B, Laloë F 2019 Quantum Mechanics (Vol. 1) (Weinheim: Wiley-VCH) pp2–32
[38] Iogansen L V 1964 Sov. Phys.-JETP 18 146
[39] Meng H, Wu X Q, Zheng Z M 2013 Europhys. Lett. 104 37003
Google Scholar
[40] Meng H, Wu J S, Wu X Q, Ren M Y, Ren Y J 2016 Sci. Rep. 6 21308
Google Scholar
下载:
计量
- 文章访问数: 2013
- PDF下载量: 74
- 被引次数: 0
