平均场反馈下全局耦合Stuart-Landau极限环系统的可解集体动力学

贺苏娟; 邹为

doi:10.7498/aps.72.20230842

摘要

耦合Stuart-Landau极限环系统为研究含振幅自由度的自持续振荡系统同步相变和集体动力学提供了一个重要的范式模型. 本文研究了平均场反馈下全局耦合Stuart-Landau极限环系统中3种典型的可解集体动力学: 非相干态、振幅死亡及锁频态. 在热力学极限$N\rightarrow\infty$情形下, 利用非相干态线性稳定性分析揭示了耦合系统中同步发生的临界条件, 发现了增强平均场反馈强度可使得耦合系统在更小的扩散耦合强度下出现同步相变行为; 通过对振幅死亡态的线性稳定性分析得到了参数空间中振幅死亡的稳定区, 发现了平均场反馈强度可有效地消除耦合系统中的振幅死亡现象; 从理论上分析了锁频态的存在性条件, 并从锁频态序参量的自洽关系中推导出了振幅死亡区的边界线. 本文的研究揭示了平均场反馈对耦合非线性系统中集体行为的动力学控制作用, 加深了平均场反馈技术对耦合诱导的集体行为影响的理解, 进一步阐释了复杂耦合系统中自组织行为的涌现规律与机制.

关键词:

Abstract

Coupled Stuart-Landau limit-cycle system serves as an important paradigmatic model for studying synchronization transitions and collective dynamics in self-sustained nonlinear systems with amplitude degree of freedom. In this paper, we extensively investigate three typical solvable collective behaviors in globally coupled Stuart-Landau limit-cycle systems under mean-field feedback: incoherence, amplitude death, and locked states. In the thermodynamic limit of $N\rightarrow\infty$, the critical condition characterizing the transition from incoherence to synchronization is explicitly obtained via performing the linear stability of the incoherent states. It is found that the synchronization transition occurs at a smaller coupling strength when the strength of mean-field feedback is gradually enhanced. The stable regions of amplitude death are theoretically obtained via an analysis of the linear stability of coupled systems around the origin. The results indicate that the existence of mean-field feedback can effectively eliminate the amplitude death phenomenon in the coupled systems; furthermore, the existence of locked states is analyzed theoretically, and in particular, the boundary of stable amplitude death region is re-derived from the self-consistent relation of the order parameter for the locked states. This work reveals the key role of mean-field feedback in controlling the collective dynamics of coupled nonlinear systems, deepens the understanding of the influence of mean-field feedback technology on the coupling-induced collective behaviors, and is conductive to our further understanding of the emerging rules and the underlying mechanisms of self-organized behavior in complex coupled systems.

Keywords:

作者及机构信息

贺苏娟,
邹为

华南师范大学数学科学学院, 广州　510631

通信作者: 邹为, weizou83@gmail.com

基金项目: 国家自然科学基金(批准号: 12075089)资助的课题.

Authors and contacts

He Su-Juan,
Zou Wei

School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China

Corresponding author: Zou Wei, weizou83@gmail.com

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 12075089).

文章全文 : translate this paragraph

参考文献

[1]	Kuramoto Y 1984 Chemical Oscillations, Waves and Turbulence (Berlin: Springer-Verlag
[2]	Pikovsky A, Rosenblum M, Kurths J 2001 Synchronization: A Universal Concept in Nonlinear Sciences (Cambridge: Cambridge University Press
[3]	Strogatz S 2003 Sync: The Emerging Science of Spontaneous Order (London: Pengiun Press Science
[4]	郑志刚 2004 耦合非线性系统的时空动力学与合作行为 (北京: 高等教育出版社) Zheng Z G 2004 Spatiotemporal Dynamics and Cooperative Behaviors in Coupled Nonlinear Systems (Beijing: Higher Education Press
[5]	丁大为, 卢小齐, 胡永兵, 杨宗立, 王威, 张红伟 2022 71 230501 Google Scholar Ding D W, Lu X Q, Hu Y B, Yang Z L, Wang W, Zhang H W 2022 Acta Phys. Sin. 71 230501 Google Scholar
[6]	蒋宏帆, 林机, 胡贝贝, 张肖 2023 72 104205 Google Scholar Jiang H F, Lin J, Hu B B, Zhang X 2023 Acta Phys. Sin. 72 104205 Google Scholar
[7]	沈力峰, 王建波, 杜占玮, 许小可 2023 72 068701 Google Scholar Shen L F, Wang J B, Du Z W, Xu X K 2023 Acta Phys. Sin. 72 068701 Google Scholar
[8]	Kuramoto Y 1975 Self-entrainment of a Population of Coupled Nonlinear Oscillators, in: International Symposium on Mathematical Problems in Theoretical Physics (Berlin Heidelberg: Springer-Verlag) pp420–428
[9]	Strogatz S H 2000 Physica D 143 1 Google Scholar
[10]	Acebrón J A, Bonilla L L, Pérez Vicente C J, Ritort F, Spigler R 2005 Rev. Mod. Phys. 77 137 Google Scholar
[11]	管曙光 2020 中国科学: 物理学力学天文学 50 010504 Google Scholar Guan S G 2020 Sci. Sin. Phys., Mech. Astron. 50 010504 Google Scholar
[12]	郑志刚, 翟云 2020 中国科学: 物理学力学天文学 50 010505 Google Scholar Zheng Z G, Zhai Y 2020 Sci. Sin. Phys., Mech. Astron. 50 010505 Google Scholar
[13]	郑志刚, 翟云, 王学彬, 陈宏斌, 徐灿 2020 69 080502 Google Scholar Zheng Z G, Zhai Y, Wang X B, Chen H B, Xu C 2020 Acta Phys. Sin. 69 080502 Google Scholar
[14]	王学彬, 徐灿, 郑志刚 2020 69 170501 Google Scholar Wang X B, Xu C, Zheng Z G 2020 Acta Phys. Sin. 69 170501 Google Scholar
[15]	蔡宗楷, 徐灿, 郑志刚 2021 70 220501 Google Scholar Cai Z K, Xu C, Zheng Z G 2021 Acta Phys. Sin. 70 220501 Google Scholar
[16]	Katz Y, Tunstrøm K, Ioannou C C, Huepe C, Couzin I D 2011 Proc. Natl. Acad. Sci. U.S.A. 108 18720 Google Scholar
[17]	Vicsek T, Zafeiris A 2012 Phys. Rep. 517 71 Google Scholar
[18]	O'Keeffe K P, Hong H, Strogatz S H 2017 Nat. Commun. 8 1504 Google Scholar
[19]	Cross M C, Hohenberg P C 1993 Rev. Mod. Phys. 65 851 Google Scholar
[20]	Nakagawa N, Kuramoto Y 1993 Prog. Theor. Phys. 89 313 Google Scholar
[21]	刘若琪, 贾萌萌, 范伟丽, 贺亚峰, 刘富成 2022 71 248201 Google Scholar Liu R Q, Jia M M, Fan W L, He Y F, Liu F C 2022 Acta Phys. Sin. 71 248201 Google Scholar
[22]	杨佳奇, 刘文军 2023 72 100504 Google Scholar Yang J Q, Liu W J 2023 Acta Phys. Sin. 72 100504 Google Scholar
[23]	Saxena G, Prasad A, Ramaswamy R 2012 Phys. Rep. 521 205 Google Scholar
[24]	Zou W, Senthilkumar D V, Zhan M, Kurths J 2021 Phys. Rep. 931 1 Google Scholar
[25]	Mirollo R E, Strogatz S H 1989 J. Stat. Phys. 60 245
[26]	Aronson D G, Ermentrout G B, Kopell N 1990 Physica D 41 403 Google Scholar
[27]	Zou W, Senthilkumar D V, Nagao R, Kiss I Z, Tang Y, Koseska A, Duan J Q, Kurths J 2015 Nat. Commun. 6 7709 Google Scholar
[28]	Ramana Reddy D V, Sen A, Johnston G L 1998 Phys. Rev. Lett. 80 5109 Google Scholar
[29]	Atay F M 2003 Phys. Rev. Lett. 91 094101 Google Scholar
[30]	Zou W, Senthilkumar D V, Zhan M, Kurths J 2013 Phys. Rev. Lett. 111 014101 Google Scholar
[31]	Konishi K 2003 Phys. Rev. E 68 067202 Google Scholar
[32]	Karnatak R, Ramaswamy R, Prasad A 2007 Phys. Rev. E 76 035201
[33]	Zou W, He S J, Yao C G 2022 Appl. Math. Lett. 131 108052 Google Scholar
[34]	Resmi V, Ambika G, Amritkar R E 2011 Phys. Rev. E 84 046212 Google Scholar
[35]	Matthews P C, Strogatz S H 1990 Phys. Rev. Lett. 65 1701 Google Scholar
[36]	Matthews P C, Mirollo R E, Strogatz S H 1991 Physica D 52 293 Google Scholar
[37]	Zou W, He S J, Senthilkumar D V, Kurths J 2023 Phys. Rev. Lett. 130 107202 Google Scholar
[38]	Schwab D J, Baetica A, Mehta P 2012 Physica D 241 1782 Google Scholar
[39]	Lee W S, Ott E, Antonsen T M 2013 Chaos 23 033116 Google Scholar
[40]	Wang C Q, Garnier N B 2016 Chaos 26 113119 Google Scholar
[41]	Kemeth F P, Haugland S W, Krischer K 2018 Phys. Rev. Lett. 120 214101 Google Scholar
[42]	Röhm A, Lüdge K, Schneider I 2018 Chaos 28 063114 Google Scholar
[43]	Kemeth F P, Haugland S W, Krischer K 2019 Chaos 29 023107 Google Scholar
[44]	León I, Pazó D 2019 Phys. Rev. E 100 012211 Google Scholar
[45]	León I, Pazó D 2020 Phys. Rev. E 102 042203
[46]	Kak S C 1993 Circuits, Systems and Signal Processing 12 263 Google Scholar
[47]	Becskei A, Séraphin B, Serrano L 2001 Embo. J. 20 2528 Google Scholar
[48]	Draghici S 1997 Int. J. Neural Syst. 8 113 Google Scholar
[49]	Gough J E, Gohm R, Yanagisawa M 2008 Phys. Rev. A 78 062104 Google Scholar
[50]	Lloyd S 2000 Phys. Rev. A 62 022108 Google Scholar
[51]	Little S, Brown P 2012 Ann. N. Y. Acad. Sci. 1265 9 Google Scholar
[52]	Chandrasekar V K, Karthiga S, Lakshmanan M 2015 Phys. Rev. E 92 012903 Google Scholar
[53]	Zhao N N, Sun Z K 2020 Int. J. Bifurcation and Chaos 30 2050094 Google Scholar
[54]	史东鑫, 李兴瑞, 单美华 2023 应用数学进展 12 1940 Google Scholar Shi D X, Li X R, Shan M H 2023 Adv. Appl. Math. 12 1940 Google Scholar

施引文献

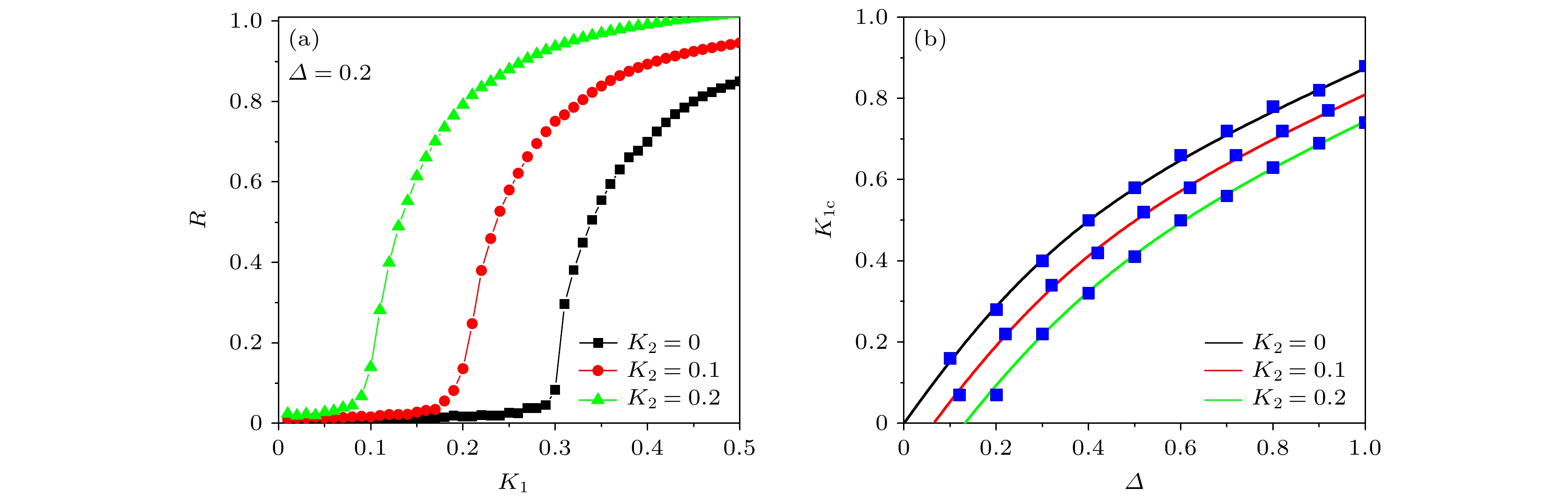
图 1 平均场反馈对全局扩散耦合系统(1)中非相干态的影响　(a) 不同平均场反馈强度$ K_2 $下, 序参量R随扩散耦合强度$ K_1 $的相变图, 其中频率标准差固定为$ \varDelta=0.2 $; (b) 不同平均场反馈强度$ K_2 $下, 使得非相干态失稳的临界扩散耦合强度$ K_{1 {\rm{c}}} $与频率标准差Δ的关系. 实线为(21)式给出的理论预测, 蓝色的方形实点为数值结果

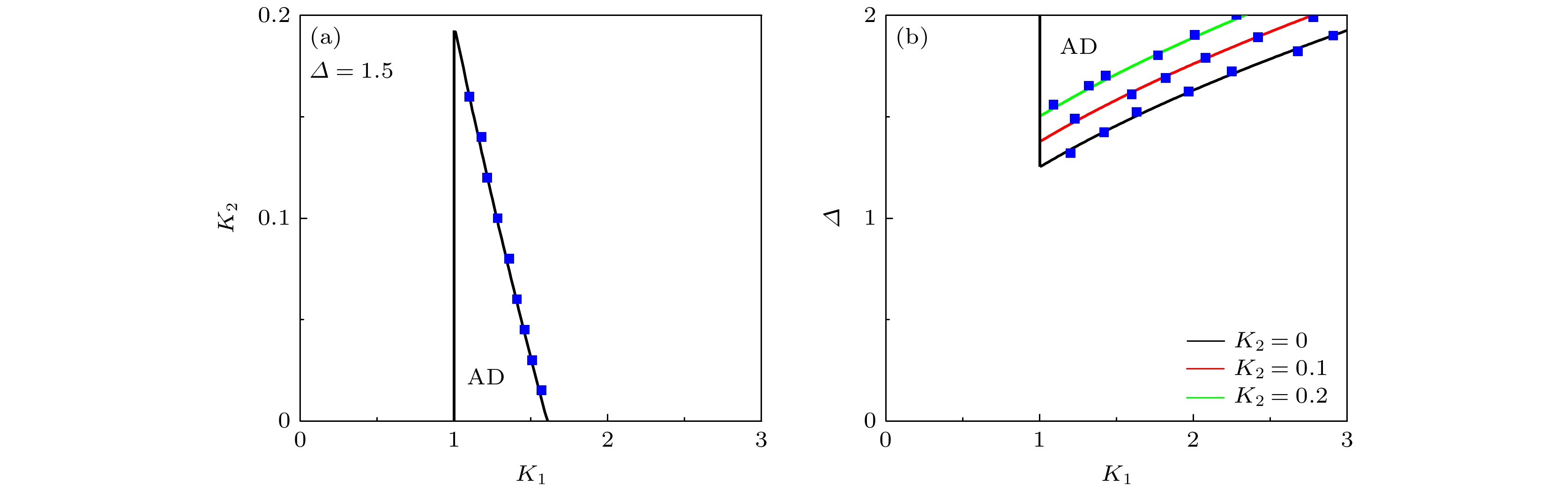
Fig. 1. Effect of mean-field feedback on the incoherence in coupled system (1): (a) Phase transition diagrams of order parameter R with the strengths of diffusive coupling $ K_1 $ under different strengths of the mean-field feedback $ K_2 $, where the standard deviation of natural frequencies is fixed at $ \varDelta=0.2 $; (b) dependence of the critical diffusive coupling strength $ K_{1 {\rm{c}}} $, beyond which the incoherence becomes destabilized, on the standard deviation Δ of natural frequencies under different strengths of the mean-field feedback $ K_2 $. The solid lines are the plots of the theoretical prediction given in Eq. (21), whereas the blue squares denote the numerical results

下载: 全尺寸图片幻灯片

图 2 平均场反馈对全局扩散耦合系统(1)中振幅死亡的影响　(a) 稳定的振幅死亡扩散耦合强度$ K_{1} $区间随平均场反馈强度$ K_2 $的变化, 其中频率标准差固定为$ \varDelta=1.5 $; (b) 不同平均场反馈强度$ K_2 $下, 参数空间$ (K_{1}, \varDelta) $中振幅死亡的稳定区. (a)与(b)中, 蓝色的方形实点表示数值模拟结果, 实斜线为(27)式中的理论预测结果

Fig. 2. Effect of mean-field feedback on amplitude death (AD) in coupled system (1): (a) Stable AD interval of diffusive coupling $ K_{1} $ versus the strength of the mean-field feedback $ K_2 $, where $ \varDelta=1.5 $ is fixed; (b) stable regions of AD in the parameter space of $ (K_{1}, \varDelta) $ under different strengths of the mean-field feedback $ K_2 $. In both panels, the blue squares represent the numerical results, whereas the solid lines denote the theoretical prediction by Eq. (27)

下载: 全尺寸图片幻灯片

map

[1]	Kuramoto Y 1984 Chemical Oscillations, Waves and Turbulence (Berlin: Springer-Verlag
[2]	Pikovsky A, Rosenblum M, Kurths J 2001 Synchronization: A Universal Concept in Nonlinear Sciences (Cambridge: Cambridge University Press
[3]	Strogatz S 2003 Sync: The Emerging Science of Spontaneous Order (London: Pengiun Press Science
[4]	郑志刚 2004 耦合非线性系统的时空动力学与合作行为 (北京: 高等教育出版社) Zheng Z G 2004 Spatiotemporal Dynamics and Cooperative Behaviors in Coupled Nonlinear Systems (Beijing: Higher Education Press
[5]	丁大为, 卢小齐, 胡永兵, 杨宗立, 王威, 张红伟 2022 71 230501 Google Scholar Ding D W, Lu X Q, Hu Y B, Yang Z L, Wang W, Zhang H W 2022 Acta Phys. Sin. 71 230501 Google Scholar
[6]	蒋宏帆, 林机, 胡贝贝, 张肖 2023 72 104205 Google Scholar Jiang H F, Lin J, Hu B B, Zhang X 2023 Acta Phys. Sin. 72 104205 Google Scholar
[7]	沈力峰, 王建波, 杜占玮, 许小可 2023 72 068701 Google Scholar Shen L F, Wang J B, Du Z W, Xu X K 2023 Acta Phys. Sin. 72 068701 Google Scholar
[8]	Kuramoto Y 1975 Self-entrainment of a Population of Coupled Nonlinear Oscillators, in: International Symposium on Mathematical Problems in Theoretical Physics (Berlin Heidelberg: Springer-Verlag) pp420–428
[9]	Strogatz S H 2000 Physica D 143 1 Google Scholar
[10]	Acebrón J A, Bonilla L L, Pérez Vicente C J, Ritort F, Spigler R 2005 Rev. Mod. Phys. 77 137 Google Scholar
[11]	管曙光 2020 中国科学: 物理学力学天文学 50 010504 Google Scholar Guan S G 2020 Sci. Sin. Phys., Mech. Astron. 50 010504 Google Scholar
[12]	郑志刚, 翟云 2020 中国科学: 物理学力学天文学 50 010505 Google Scholar Zheng Z G, Zhai Y 2020 Sci. Sin. Phys., Mech. Astron. 50 010505 Google Scholar
[13]	郑志刚, 翟云, 王学彬, 陈宏斌, 徐灿 2020 69 080502 Google Scholar Zheng Z G, Zhai Y, Wang X B, Chen H B, Xu C 2020 Acta Phys. Sin. 69 080502 Google Scholar
[14]	王学彬, 徐灿, 郑志刚 2020 69 170501 Google Scholar Wang X B, Xu C, Zheng Z G 2020 Acta Phys. Sin. 69 170501 Google Scholar
[15]	蔡宗楷, 徐灿, 郑志刚 2021 70 220501 Google Scholar Cai Z K, Xu C, Zheng Z G 2021 Acta Phys. Sin. 70 220501 Google Scholar
[16]	Katz Y, Tunstrøm K, Ioannou C C, Huepe C, Couzin I D 2011 Proc. Natl. Acad. Sci. U.S.A. 108 18720 Google Scholar
[17]	Vicsek T, Zafeiris A 2012 Phys. Rep. 517 71 Google Scholar
[18]	O'Keeffe K P, Hong H, Strogatz S H 2017 Nat. Commun. 8 1504 Google Scholar
[19]	Cross M C, Hohenberg P C 1993 Rev. Mod. Phys. 65 851 Google Scholar
[20]	Nakagawa N, Kuramoto Y 1993 Prog. Theor. Phys. 89 313 Google Scholar
[21]	刘若琪, 贾萌萌, 范伟丽, 贺亚峰, 刘富成 2022 71 248201 Google Scholar Liu R Q, Jia M M, Fan W L, He Y F, Liu F C 2022 Acta Phys. Sin. 71 248201 Google Scholar
[22]	杨佳奇, 刘文军 2023 72 100504 Google Scholar Yang J Q, Liu W J 2023 Acta Phys. Sin. 72 100504 Google Scholar
[23]	Saxena G, Prasad A, Ramaswamy R 2012 Phys. Rep. 521 205 Google Scholar
[24]	Zou W, Senthilkumar D V, Zhan M, Kurths J 2021 Phys. Rep. 931 1 Google Scholar
[25]	Mirollo R E, Strogatz S H 1989 J. Stat. Phys. 60 245
[26]	Aronson D G, Ermentrout G B, Kopell N 1990 Physica D 41 403 Google Scholar
[27]	Zou W, Senthilkumar D V, Nagao R, Kiss I Z, Tang Y, Koseska A, Duan J Q, Kurths J 2015 Nat. Commun. 6 7709 Google Scholar
[28]	Ramana Reddy D V, Sen A, Johnston G L 1998 Phys. Rev. Lett. 80 5109 Google Scholar
[29]	Atay F M 2003 Phys. Rev. Lett. 91 094101 Google Scholar
[30]	Zou W, Senthilkumar D V, Zhan M, Kurths J 2013 Phys. Rev. Lett. 111 014101 Google Scholar
[31]	Konishi K 2003 Phys. Rev. E 68 067202 Google Scholar
[32]	Karnatak R, Ramaswamy R, Prasad A 2007 Phys. Rev. E 76 035201
[33]	Zou W, He S J, Yao C G 2022 Appl. Math. Lett. 131 108052 Google Scholar
[34]	Resmi V, Ambika G, Amritkar R E 2011 Phys. Rev. E 84 046212 Google Scholar
[35]	Matthews P C, Strogatz S H 1990 Phys. Rev. Lett. 65 1701 Google Scholar
[36]	Matthews P C, Mirollo R E, Strogatz S H 1991 Physica D 52 293 Google Scholar
[37]	Zou W, He S J, Senthilkumar D V, Kurths J 2023 Phys. Rev. Lett. 130 107202 Google Scholar
[38]	Schwab D J, Baetica A, Mehta P 2012 Physica D 241 1782 Google Scholar
[39]	Lee W S, Ott E, Antonsen T M 2013 Chaos 23 033116 Google Scholar
[40]	Wang C Q, Garnier N B 2016 Chaos 26 113119 Google Scholar
[41]	Kemeth F P, Haugland S W, Krischer K 2018 Phys. Rev. Lett. 120 214101 Google Scholar
[42]	Röhm A, Lüdge K, Schneider I 2018 Chaos 28 063114 Google Scholar
[43]	Kemeth F P, Haugland S W, Krischer K 2019 Chaos 29 023107 Google Scholar
[44]	León I, Pazó D 2019 Phys. Rev. E 100 012211 Google Scholar
[45]	León I, Pazó D 2020 Phys. Rev. E 102 042203
[46]	Kak S C 1993 Circuits, Systems and Signal Processing 12 263 Google Scholar
[47]	Becskei A, Séraphin B, Serrano L 2001 Embo. J. 20 2528 Google Scholar
[48]	Draghici S 1997 Int. J. Neural Syst. 8 113 Google Scholar
[49]	Gough J E, Gohm R, Yanagisawa M 2008 Phys. Rev. A 78 062104 Google Scholar
[50]	Lloyd S 2000 Phys. Rev. A 62 022108 Google Scholar
[51]	Little S, Brown P 2012 Ann. N. Y. Acad. Sci. 1265 9 Google Scholar
[52]	Chandrasekar V K, Karthiga S, Lakshmanan M 2015 Phys. Rev. E 92 012903 Google Scholar
[53]	Zhao N N, Sun Z K 2020 Int. J. Bifurcation and Chaos 30 2050094 Google Scholar
[54]	史东鑫, 李兴瑞, 单美华 2023 应用数学进展 12 1940 Google Scholar Shi D X, Li X R, Shan M H 2023 Adv. Appl. Math. 12 1940 Google Scholar

[1]	赵中华, 渠广昊, 姚佳池, 闵道敏, 翟鹏飞, 刘杰, 李盛涛. 热峰作用下单斜ZrO₂相变过程的分子动力学模拟. , 2021, 70(13): 136101. doi: 10.7498/aps.70.20201861
[2]	刘妮, 张小芳, 梁九卿. 双光腔光机械系统的动力学相变和选择性能量交换. , 2021, 70(14): 140301. doi: 10.7498/aps.70.20210178
[3]	蔡宗楷, 徐灿, 郑志刚. 高阶耦合相振子系统的同步动力学. , 2021, 70(22): 220501. doi: 10.7498/aps.70.20211206
[4]	刘妮, 黄珊, 李军奇, 梁九卿. 有限温度下腔光机械系统中N个二能级原子的相变和热力学性质. , 2019, 68(19): 193701. doi: 10.7498/aps.68.20190347
[5]	种涛, 王桂吉, 谭福利, 赵剑衡, 唐志平. 窗口声阻抗对锆相变动力学的影响. , 2018, 67(7): 070204. doi: 10.7498/aps.67.20172198
[6]	李鹤龄, 王娟娟, 杨斌, 沈宏君. 由N-E-V分布及赝势法研究弱磁场中弱相互作用费米子气体的热力学性质. , 2015, 64(4): 040501. doi: 10.7498/aps.64.040501
[7]	蒋招绣, 辛铭之, 申海艇, 王永刚, 聂恒昌, 刘雨生. 多孔未极化Pb(Zr0.95Ti0.05)O3铁电陶瓷单轴压缩力学响应与相变. , 2015, 64(13): 134601. doi: 10.7498/aps.64.134601
[8]	王立明, 吴峰. 耦合方式与初始条件结构对分数阶双稳态振子环形网络同步的影响. , 2014, 63(5): 050503. doi: 10.7498/aps.63.050503
[9]	刘本琼, 谢雷, 段晓溪, 孙光爱, 陈波, 宋建明, 刘耀光, 汪小琳. 铀的结构相变及力学性能的第一性原理计算. , 2013, 62(17): 176104. doi: 10.7498/aps.62.176104
[10]	王立明, 吴峰. 耦合分数阶双稳态振子的同步、反同步与振幅死亡. , 2013, 62(21): 210504. doi: 10.7498/aps.62.210504
[11]	孙光爱, 王虹, 汪小琳, 陈波, 常丽丽, 刘耀光, 盛六四, Woo W, Kang MY. 原位中子衍射研究两相NiTi合金的微力学相互作用和相变机理. , 2012, 61(22): 226102. doi: 10.7498/aps.61.226102
[12]	周婷婷, 黄风雷. HMX不同晶型热膨胀特性及相变的ReaxFF分子动力学模拟. , 2012, 61(24): 246501. doi: 10.7498/aps.61.246501
[13]	谭红芳, 金涛, 屈世显. 一个全局耦合不连续映像格子中的冻结化随机图案模式. , 2012, 61(4): 040507. doi: 10.7498/aps.61.040507
[14]	汪志刚, 吴亮, 张杨, 文玉华. 面心立方铁纳米粒子的相变与并合行为的分子动力学研究. , 2011, 60(9): 096105. doi: 10.7498/aps.60.096105
[15]	王海燕, 崔红保, 历长云, 李旭升, 王狂飞. AlAs相变及热动力学性质的第一性原理研究. , 2009, 58(8): 5598-5603. doi: 10.7498/aps.58.5598
[16]	邵建立, 秦承森, 王裴. 动态压缩下马氏体相变力学性质的微观研究. , 2009, 58(3): 1936-1941. doi: 10.7498/aps.58.1936
[17]	陈贺胜. 带有2+1味道Wilson费米子的格点量子色动力学在有限温度、有限密度下的相变. , 2009, 58(10): 6791-6797. doi: 10.7498/aps.58.6791
[18]	邵建立, 王裴, 秦承森, 周洪强. 铁冲击相变的分子动力学研究. , 2007, 56(9): 5389-5393. doi: 10.7498/aps.56.5389
[19]	何文平, 封国林, 高新全, 李建平. 无反馈作用下混沌系统的振幅死亡. , 2006, 55(11): 6192-6196. doi: 10.7498/aps.55.6192
[20]	马文麒, 杨承辉. 一类耦合非线性振子同步混沌Hopf分岔及其电路仿真. , 2005, 54(3): 1064-1070. doi: 10.7498/aps.54.1064

计量

文章访问数: 1996
PDF下载量: 58
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

平均场反馈下全局耦合Stuart-Landau极限环系统的可解集体动力学