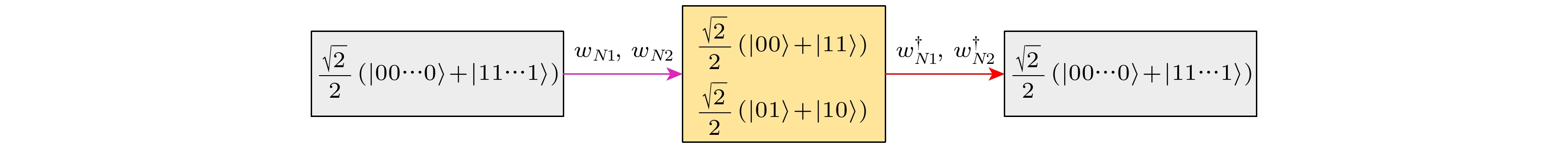-
等距张量(即张量
$ {\boldsymbol{\omega }} $ 满足$ {{\boldsymbol{\omega }}^\dagger }{\boldsymbol{\omega }} = {\boldsymbol{I}} $ )为实现张量网络态(tensor network states, TNSs)中确定纠缠态的压缩提供了一种新颖而强大的数学构造算法. 结合等距张量, 本文发现在量子密钥分发(quantum key distribution, QKD)中可能采取完全不同的密钥生成方法, 即在不改变纠缠态结构和性质的情况下, 将任意多光子纠缠态压缩成单光子态或者Bell态. 在提出的QKD协议中, 输入态由任意纠缠态组成, 这些输入态首先被发送方Alice压缩成单光子态$ \left| 0 \right\rangle $ 或$ \left| 1 \right\rangle $ 或Bell态, 使得提出的协议同时达到了多模存储和确定性传输的要求, 且减少了需要传输和存储的量子比特数量, 从而提高了QKD协议的编码能力. 然后再添加诱骗态在这些单光子态$ \left| 0 \right\rangle $ 和$ \left| 1 \right\rangle $ 中, 再通过量子信道一起发送给接收方Bob, 以制备密钥. 最后, Alice和Bob利用筛选出来的压缩态|0$\rangle $ 和|1$\rangle $ 以及他们对应的等距张量的共轭转置来协商出共享密钥. 本文提出的协议比一般协议中的单光子能编码更多的经典比特, 显著提高了编码效率, 减少了量子资源的使用. 本文提出的QKD协议还保持了生成密钥的完美安全性.Isometric tensor offers a novel and powerful tool that can compress an entangled state into its tensor network state (TNS). The resulting quantum compression provides a new opportunity for enhancing quantum key distribution (QKD) protocols. The main idea explored in this work is to use the quantum compression to improve the efficiency of QKD. In a nut-shell, a collection of any multi-photon entangled states that carry encoded classical bits is compressed into a single-photon state before the corresponding photon is sent to the receiver that measures the qubit and decompresses it. In this paper, we first show how to obtain the generalized isometric tensors for compressing any entangled states and their inverse isometric tensors for decompression. In our proposed QKD protocol, the input state consists of any multi-photon entangled states, which are first compressed into a single-photon state$ \left| 0 \right\rangle $ or$ \left| 1 \right\rangle $ or Bell states by the sender Alice. A sequence of single-photon states$ \left| 0 \right\rangle $ and$ \left| 1 \right\rangle $ and one photon from the Bell state mixed with decoy qubits is sent to the receiver Bob via a quantum channel. Bob obtains the final sifted compressed states$ \left| 0 \right\rangle $ and$ \left| 1 \right\rangle $ and conjugate transpose of the isometric tensors. Using our protocols, Bob can decompress the received states$ \left| 0 \right\rangle $ and$ \left| 1 \right\rangle $ into original entangled states. Since quantum processors that are used to send quantum information between nodes are relatively primitive and low in power and the preparation of many-photon entanglement is relatively difficult at present, finding suitable protocols for the compression of transmitted quantum data brings important practical benefits. More generally, the quantum information theory primarily investigates quantum data manipulation under locality constraints, so our protocols connect naturally to these investigations. Our protocols increase the encoding capacity of QKD protocols. Not only our proposed processes of compression and decompression are very simple, but also entanglement compression using isometric tensors can be implemented by using quantum circuits and current technology. Because many ideas for designing of quantum information processing equipment envision that a network composed of relatively small quantum processors sending quantum information between nodes, it is greatly significant to find appropriate protocols for compressing the transmitted quantum data .-
Keywords:
- entanglement compression /
- generalized isometric tensors /
- tensor network states /
- decompression
[1] Bennett C H, Brassard G 1984 Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing Bangalore, India, December 10–12, 1984 pp175–179
[2] Wang B, Zhang B F, Zou F C, et al. 2021 Optik 235 166628
 Google Scholar
Google Scholar
[3] Ekert A K 1991 Phys. Rev. Lett. 67 661
 Google Scholar
Google Scholar
[4] Bennett C H, Brassard G, Mermin N D 1992 Phys. Rev. Lett. 68 557
 Google Scholar
Google Scholar
[5] Greenberger D M, Horne M A, Zeilinger A 1989 Bell’s Theorem, Quantum Theory and Conceptions of the Universe (Dordrecht: Springer) pp69–72
[6] Bouwmeester D, Pan J W, Daniell M, Weinfurter H, Zeilinger A 1999 Phys. Rev. Lett. 82 1345
 Google Scholar
Google Scholar
[7] Guo Y, Shi R, Zeng G 2010 Phys. Scr. 81 045006
 Google Scholar
Google Scholar
[8] Xu G B, Wen Q Y, Gao F, Qin S J 2014 Quantum Inf. Process. 13 2587
 Google Scholar
Google Scholar
[9] Castañeda Valle D, Quezada L F, Dong S H 2021 Ann. Phys. Berlin 533 2100116
 Google Scholar
Google Scholar
[10] Zhao N, Guo X, Wu T 2021 Phys. Rev. A 104 062616
 Google Scholar
Google Scholar
[11] Upadhyaya T, van Himbeeck T, Lin J, et al. 2021 PRX Quantum. 2 020325
 Google Scholar
Google Scholar
[12] Jiang C, Yu Z W, Hu X L, Wang X B 2021 Phys. Rev. A 103 012402
 Google Scholar
Google Scholar
[13] Lim C C W, Xu F, Pan J W, Ekert A 2021 Phys. Rev. Lett. 126 100501
 Google Scholar
Google Scholar
[14] Long G L and Liu X S 2002 Phys. Rev. A 65 032302
 Google Scholar
Google Scholar
[15] Chang C H, Yang C W, Hwang T 2016 Int. J. Theor. Phys. 55 3993
 Google Scholar
Google Scholar
[16] Pivoluska M, Huber M, Malik M 2018 Phys. Rev. A 97 032312
 Google Scholar
Google Scholar
[17] Zhu K N, Zhou N R, Wang Y Q, et al. 2018 Int. J. Theor. Phys. 57 3621
 Google Scholar
Google Scholar
[18] Zhou H, Lv K, Huang L, et al. 2022 IEEE/ACM T. Network. 30 1328
 Google Scholar
Google Scholar
[19] Wang X L, Chen L K, Li W, Huang H L, Liu C, Chen C, Luo Y H, Su Z E, Wu D, Li Z D, Lu H, Hu Y, Jiang X, Peng C Z, Li L, Liu N L, Chen Y A, Lu C Y, Pan J W 2016 Phys. Rev. Lett. 117 210502
 Google Scholar
Google Scholar
[20] Xia Y, Lu P M, Zeng Y Z 2012 Quantum Inf. Process. 11 605
 Google Scholar
Google Scholar
[21] Huang Y F, Liu B H, Peng L, et al. 2011 Nat. Commun. 2 1
[22] Xia Y, Song J, Ning Y, et al. 2010 JETP Lett. 90 735
 Google Scholar
Google Scholar
[23] Svozil K 2022 Found. Phys. 52 4
 Google Scholar
Google Scholar
[24] Yin H L, Fu Y, Li C L, et al. 2023 Nati. Sci. Rev. 10 228
 Google Scholar
Google Scholar
[25] Xie Y M, Lu Y S, Weng C X, et al. 2022 PRX Quantum. 3 020315
 Google Scholar
Google Scholar
[26] Gu J, Cao X Y, Fu Y, et al. 2022 Sci. Bull. 67 2167
 Google Scholar
Google Scholar
[27] Fan C R, Lu B, Feng X T, et al. 2021 Quant. Engineer. 3 e67
[28] Bostroem K, Felbinger T 2002 Phys. Rev. A 65 032313
 Google Scholar
Google Scholar
[29] Datta N, Renes J M, Renner R, et al. 2013 IEEE Inform. Theory 59 8057
 Google Scholar
Google Scholar
[30] Plesch M, Bužek V 2010 Phys. Rev. A 81 032317
 Google Scholar
Google Scholar
[31] Rozema L A, Mahler D H, Hayat A, Turner P S, Steinberg A M 2014 Phys. Rev. Lett. 113 160504
 Google Scholar
Google Scholar
[32] Yang Y, Chiribella G, Ebler D 2016 Phys. Rev. Lett. 116 080501
 Google Scholar
Google Scholar
[33] Yang Y, Chiribella G, Hayashi M 2016 Phys. Rev. Lett. 117 090502
 Google Scholar
Google Scholar
[34] Romero J, Olson J P, Aspuru-Guzik A 2017 Quantum Sci. Technol. 2 045001
 Google Scholar
Google Scholar
[35] Pepper A, Tischler N, Pryde G J 2019 Phys. Rev. Lett. 122 060501
 Google Scholar
Google Scholar
[36] Van Acoleyen K, Hallam A, Bal M, Hauru M, Haegeman J, Verstraete F 2020 Phys. Rev. B 102 165131
 Google Scholar
Google Scholar
[37] Lai H, Pieprzyk J, Pan L 2023 Sci. China Inf. Sc. 66 180510
 Google Scholar
Google Scholar
[38] Evenbly G 2022 Front. Phys. 10 1146
[39] Bennett C H, DiVincenzo D P, Smolin J A, Wootters W K 1996 Phys. Rev. A 54 3824
 Google Scholar
Google Scholar
-
图 1 利用wN1, wN2, N光子GHZ 纠缠态
$ ({{\sqrt 2 }}/{2})\left( {\left| {00 \cdots 0} \right\rangle + \left| {11 \cdots 1} \right\rangle } \right) $ 被随机压缩为数态$| 0 \rangle $ 或$| 1\rangle $ , 利用${\boldsymbol{w}}_{N1}^{\dagger},{\boldsymbol{w}}_{N2}^{\dagger}$ ,$| 0 \rangle $ 或$| 1 \rangle $ 被解压缩为N光子GHZ 纠缠态$({{\sqrt 2 }}/{2})\left( {\left| {00 \cdots 0} \right\rangle + \left| {11 \cdots 1} \right\rangle } \right)$ 示意图Fig. 1. The schematic compression of
$({{\sqrt 2 }}/{2})\left( {\left| {00 \cdots 0} \right\rangle + \left| {11 \cdots 1} \right\rangle } \right)$ into$\left| 0 \right\rangle $ or$\left| 1 \right\rangle $ using${{\boldsymbol{w}}_{N1}}, {{\boldsymbol{w}}_{N2}}$ , and decompression of$\left| 0 \right\rangle $ or$\left| 1 \right\rangle $ into$({{\sqrt 2 }}/{2})\left( {\left| {00 \cdots 0} \right\rangle + \left| {11 \cdots 1} \right\rangle } \right)$ using${\boldsymbol{w}}_{N1}^\dagger ,{\boldsymbol{w}}_{N2}^\dagger$ .图 2 利用
${\boldsymbol{w}}'_{N1}, {\boldsymbol{w}}'_{N2}$ , N 光子 GHZ 纠缠态$({{\sqrt 2 }}/{2})\left( {\left| {00 \cdots 0} \right\rangle + \left| {11 \cdots 1} \right\rangle } \right)$ 被随机压缩为Bell态$({{\sqrt 2 }}/{2})\left( {\left| {00} \right\rangle + \left| {11} \right\rangle } \right)$ 或$({{\sqrt 2 }}/{2}) ( | 01 \rangle + $ $ |10\rangle)$ , 利用${\boldsymbol{w}}^{\prime\dagger}_{N1}, {\boldsymbol{w}}^{\prime\dagger}_{N2}$ , Bell态$({{\sqrt 2 }}/{2})\left( {\left| {00} \right\rangle + \left| {11} \right\rangle } \right)$ 或$({{\sqrt 2 }}/{2})\left( {\left| {01} \right\rangle + \left| {10} \right\rangle } \right)$ 被解压缩为N 光子 GHZ 纠缠态$({{\sqrt 2 }}/{2}) (| 00 \cdots 0\rangle + $ $ | 11 \cdots 1\rangle)$ 示意图Fig. 2. The schematic compression of
$({{\sqrt 2 }}/{2})\left( {\left| {00 \cdots 0} \right\rangle + \left| {11 \cdots 1} \right\rangle } \right)$ into$({{\sqrt 2 }}/{2})\left( {\left| {00} \right\rangle + \left| {11} \right\rangle } \right)$ or$({{\sqrt 2 }}/{2})\left( {\left| {01} \right\rangle + \left| {10} \right\rangle } \right)$ using${{\boldsymbol{w}}'_{N1}}, $ $ {{\boldsymbol{w}}'_{N2}}$ , and decompression of$({{\sqrt 2 }}/{2})\left( {\left| {00} \right\rangle + \left| {11} \right\rangle } \right)$ or$({{\sqrt 2 }}/{2})\left( {\left| {01} \right\rangle + \left| {10} \right\rangle } \right)$ into$({{\sqrt 2 }}/{2})\left( {\left| {00 \cdots 0} \right\rangle + \left| {11 \cdots 1} \right\rangle } \right)$ using${\boldsymbol{w}}_{N1}^{\prime\dagger} , {\boldsymbol{w}}_{N2}^{\prime\dagger }$ .表 1 压缩纠缠态用于在 Alice 和 Bob 之间生成密钥的例子
Table 1. An example of transmitting the compressed entangled state for generating a secret key between Alice and Bob.
Alice随机制备纠缠态 $ ({{\sqrt 2 }}/{2})\left( {\left| {000} \right\rangle + \left| {111} \right\rangle } \right) $ $ ({{\sqrt 2 }}/{2})\left( {\left| {0000} \right\rangle + \left| {1111} \right\rangle } \right) $ $ N(N \geqslant 5) $光子GHZ态 Alice随机选择等距张量 $ {{\boldsymbol{w}}_{31}} $ $ {{\boldsymbol{w}}_{{4}1}} $ $ {{\boldsymbol{w}}_{N2}} $ Alice压缩纠缠态 $ \left| 0 \right\rangle $ $ \left| 0 \right\rangle $ $ \left| 0 \right\rangle $ Alice随机选择测量基 $ {B_x} $ $ {B_{\text{z}}} $ ${B_z}$ Bob随机选择测量基 ${B_z}$ $ {B_{\text{z}}} $ $ {B_x} $ 对基 否 是 否 筛选出的共享压缩态 — $ \left| 0 \right\rangle $ — 解压缩共享压缩态 — $ ({{\sqrt 2 }}/{2})\left( {\left| {0000} \right\rangle + \left| {1111} \right\rangle } \right) $ — -
[1] Bennett C H, Brassard G 1984 Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing Bangalore, India, December 10–12, 1984 pp175–179
[2] Wang B, Zhang B F, Zou F C, et al. 2021 Optik 235 166628
 Google Scholar
Google Scholar
[3] Ekert A K 1991 Phys. Rev. Lett. 67 661
 Google Scholar
Google Scholar
[4] Bennett C H, Brassard G, Mermin N D 1992 Phys. Rev. Lett. 68 557
 Google Scholar
Google Scholar
[5] Greenberger D M, Horne M A, Zeilinger A 1989 Bell’s Theorem, Quantum Theory and Conceptions of the Universe (Dordrecht: Springer) pp69–72
[6] Bouwmeester D, Pan J W, Daniell M, Weinfurter H, Zeilinger A 1999 Phys. Rev. Lett. 82 1345
 Google Scholar
Google Scholar
[7] Guo Y, Shi R, Zeng G 2010 Phys. Scr. 81 045006
 Google Scholar
Google Scholar
[8] Xu G B, Wen Q Y, Gao F, Qin S J 2014 Quantum Inf. Process. 13 2587
 Google Scholar
Google Scholar
[9] Castañeda Valle D, Quezada L F, Dong S H 2021 Ann. Phys. Berlin 533 2100116
 Google Scholar
Google Scholar
[10] Zhao N, Guo X, Wu T 2021 Phys. Rev. A 104 062616
 Google Scholar
Google Scholar
[11] Upadhyaya T, van Himbeeck T, Lin J, et al. 2021 PRX Quantum. 2 020325
 Google Scholar
Google Scholar
[12] Jiang C, Yu Z W, Hu X L, Wang X B 2021 Phys. Rev. A 103 012402
 Google Scholar
Google Scholar
[13] Lim C C W, Xu F, Pan J W, Ekert A 2021 Phys. Rev. Lett. 126 100501
 Google Scholar
Google Scholar
[14] Long G L and Liu X S 2002 Phys. Rev. A 65 032302
 Google Scholar
Google Scholar
[15] Chang C H, Yang C W, Hwang T 2016 Int. J. Theor. Phys. 55 3993
 Google Scholar
Google Scholar
[16] Pivoluska M, Huber M, Malik M 2018 Phys. Rev. A 97 032312
 Google Scholar
Google Scholar
[17] Zhu K N, Zhou N R, Wang Y Q, et al. 2018 Int. J. Theor. Phys. 57 3621
 Google Scholar
Google Scholar
[18] Zhou H, Lv K, Huang L, et al. 2022 IEEE/ACM T. Network. 30 1328
 Google Scholar
Google Scholar
[19] Wang X L, Chen L K, Li W, Huang H L, Liu C, Chen C, Luo Y H, Su Z E, Wu D, Li Z D, Lu H, Hu Y, Jiang X, Peng C Z, Li L, Liu N L, Chen Y A, Lu C Y, Pan J W 2016 Phys. Rev. Lett. 117 210502
 Google Scholar
Google Scholar
[20] Xia Y, Lu P M, Zeng Y Z 2012 Quantum Inf. Process. 11 605
 Google Scholar
Google Scholar
[21] Huang Y F, Liu B H, Peng L, et al. 2011 Nat. Commun. 2 1
[22] Xia Y, Song J, Ning Y, et al. 2010 JETP Lett. 90 735
 Google Scholar
Google Scholar
[23] Svozil K 2022 Found. Phys. 52 4
 Google Scholar
Google Scholar
[24] Yin H L, Fu Y, Li C L, et al. 2023 Nati. Sci. Rev. 10 228
 Google Scholar
Google Scholar
[25] Xie Y M, Lu Y S, Weng C X, et al. 2022 PRX Quantum. 3 020315
 Google Scholar
Google Scholar
[26] Gu J, Cao X Y, Fu Y, et al. 2022 Sci. Bull. 67 2167
 Google Scholar
Google Scholar
[27] Fan C R, Lu B, Feng X T, et al. 2021 Quant. Engineer. 3 e67
[28] Bostroem K, Felbinger T 2002 Phys. Rev. A 65 032313
 Google Scholar
Google Scholar
[29] Datta N, Renes J M, Renner R, et al. 2013 IEEE Inform. Theory 59 8057
 Google Scholar
Google Scholar
[30] Plesch M, Bužek V 2010 Phys. Rev. A 81 032317
 Google Scholar
Google Scholar
[31] Rozema L A, Mahler D H, Hayat A, Turner P S, Steinberg A M 2014 Phys. Rev. Lett. 113 160504
 Google Scholar
Google Scholar
[32] Yang Y, Chiribella G, Ebler D 2016 Phys. Rev. Lett. 116 080501
 Google Scholar
Google Scholar
[33] Yang Y, Chiribella G, Hayashi M 2016 Phys. Rev. Lett. 117 090502
 Google Scholar
Google Scholar
[34] Romero J, Olson J P, Aspuru-Guzik A 2017 Quantum Sci. Technol. 2 045001
 Google Scholar
Google Scholar
[35] Pepper A, Tischler N, Pryde G J 2019 Phys. Rev. Lett. 122 060501
 Google Scholar
Google Scholar
[36] Van Acoleyen K, Hallam A, Bal M, Hauru M, Haegeman J, Verstraete F 2020 Phys. Rev. B 102 165131
 Google Scholar
Google Scholar
[37] Lai H, Pieprzyk J, Pan L 2023 Sci. China Inf. Sc. 66 180510
 Google Scholar
Google Scholar
[38] Evenbly G 2022 Front. Phys. 10 1146
[39] Bennett C H, DiVincenzo D P, Smolin J A, Wootters W K 1996 Phys. Rev. A 54 3824
 Google Scholar
Google Scholar
计量
- 文章访问数: 3617
- PDF下载量: 78
- 被引次数: 0




















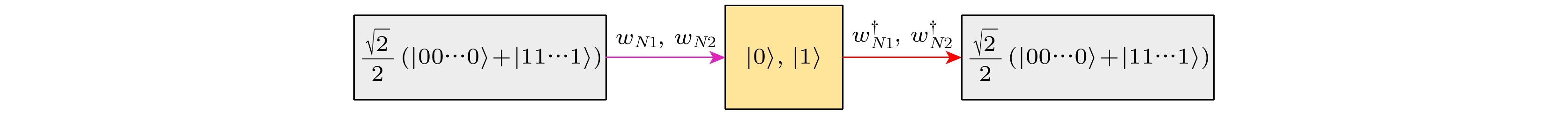















 下载:
下载: