-
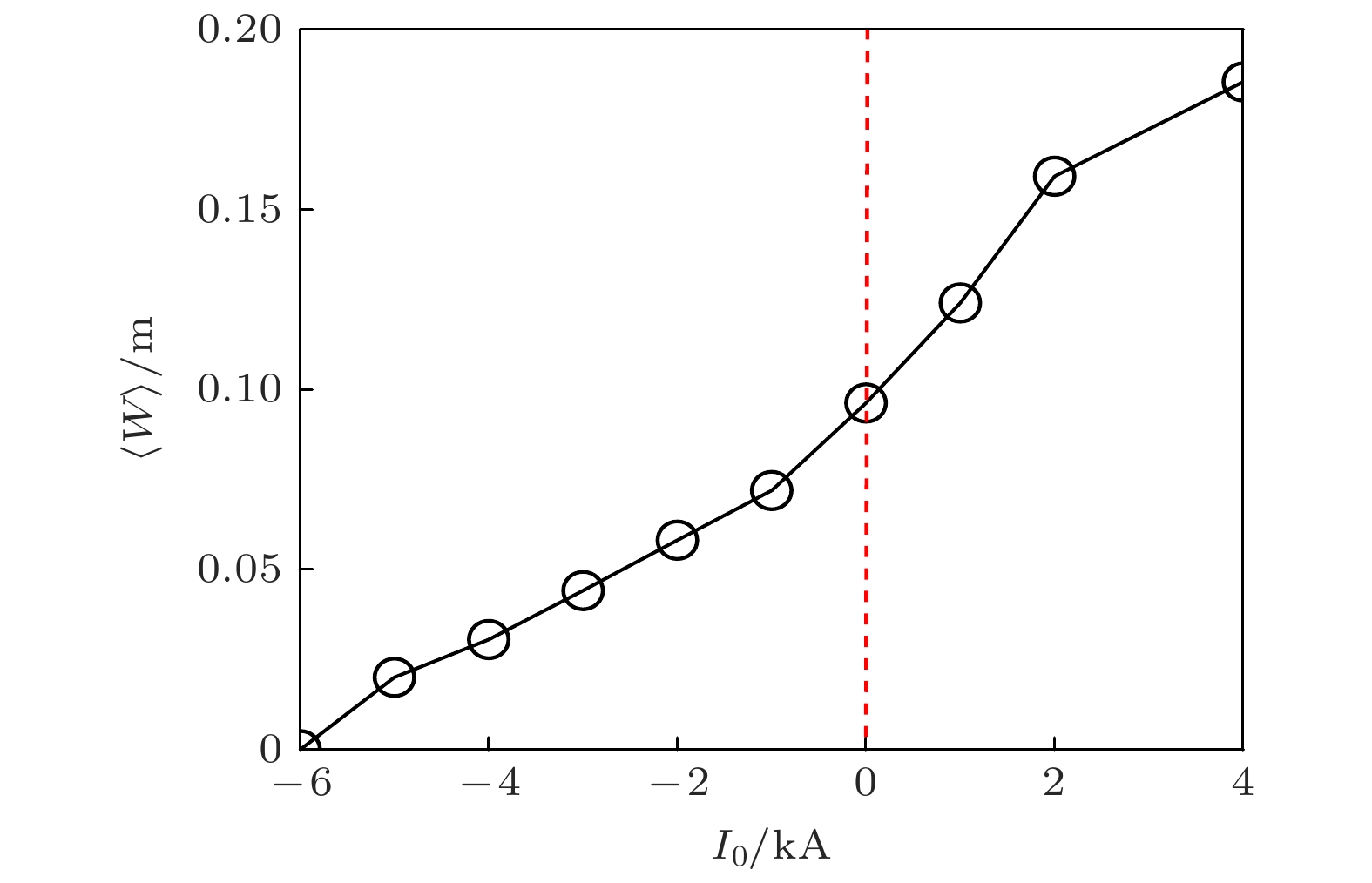
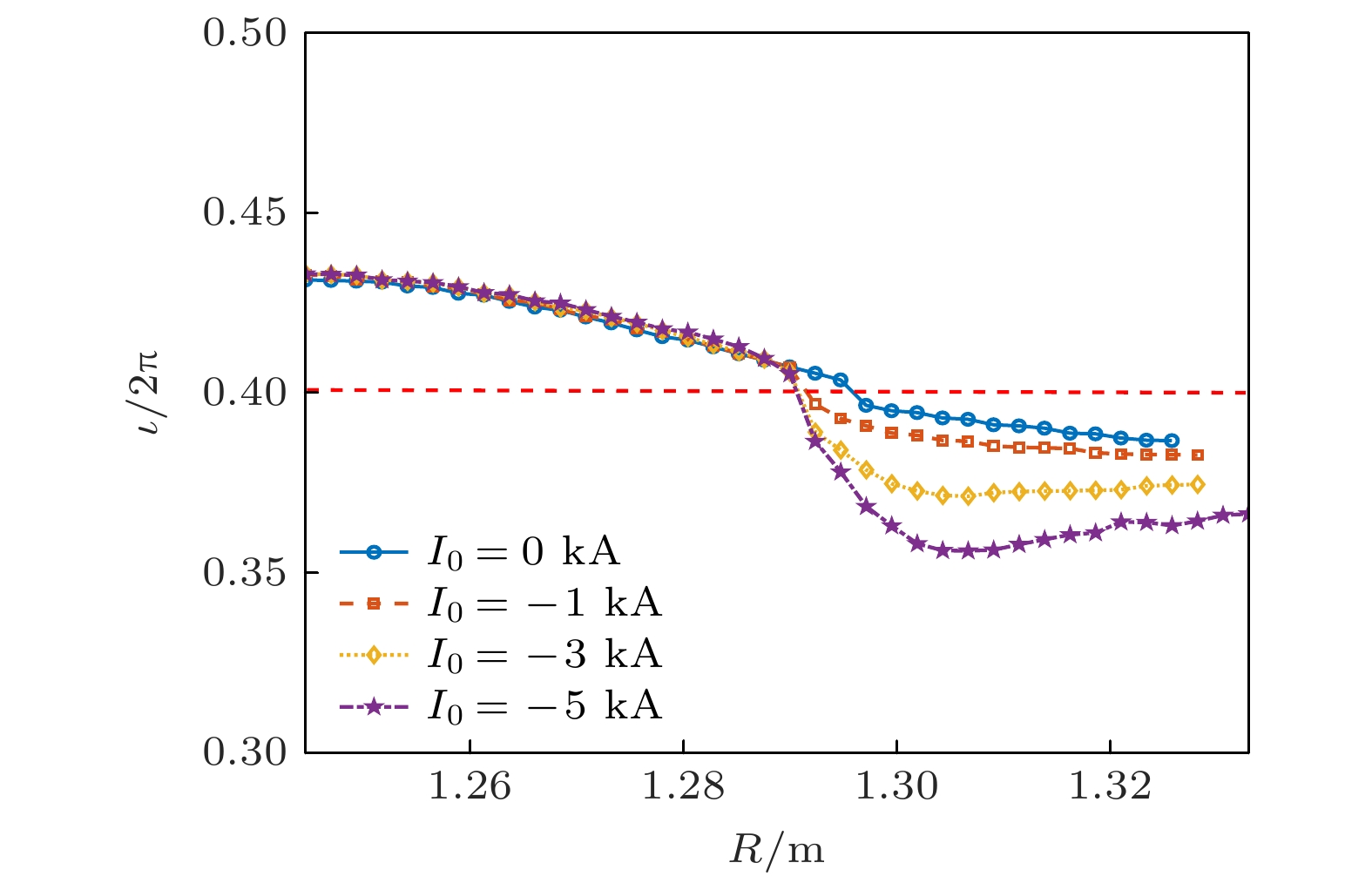
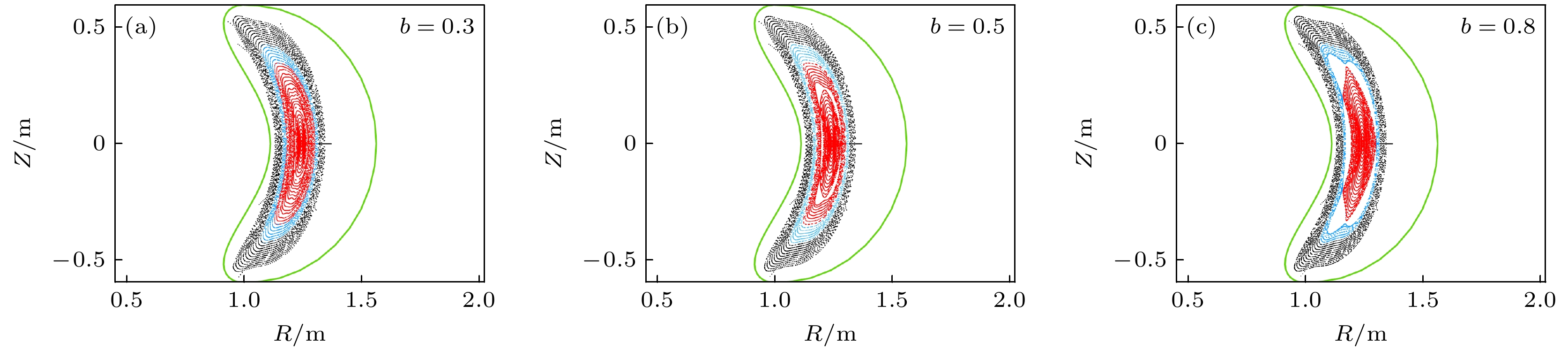
环形磁约束等离子体中产生的磁岛因为磁场的旋转变换而具有三维螺旋结构, 特别是仿星器位形下平衡磁面就呈三维螺旋性质. 因此, 仿星器磁岛形成及其不稳定性是环形磁约束三维物理的典型问题, 也是仿星器物理研究的重点课题之一. 早期研究表明, 非感应电流驱动(如电子回旋电流驱动(ECCD))所产生的环向电流对磁岛具有一定的抑制/控制作用. 为弄清中国首台准环对称仿星器CFQS低参数运行模式下三维磁岛物理, 本文聚焦在低比压(β)等离子体, 忽略自举电流并通过调控环向场线圈电流以产生旋转变换(ι/2π)为0.4的有理面, 利用HINT代码模拟研究低比压等离子体中环向电流驱动对m/n = 5/2磁岛的影响, m为极向模数, n为环向模数. 研究表明, 在常数电流情况下, 当电流方向为正/负方向时, 电流对磁岛具有较强的激发/抑制作用. 当负方向的电流大于6 kA时, 磁岛将被完全被抑制, 主要原因是环向电流驱动通过改变旋转变换剖面, 使其避开ι/2π = 0.4的有理面, 导致m/n = 5/2三维磁岛不满足共振激发条件, 最终磁岛的增长被抑制. 而在局域电流分布情况下, 磁岛的抑制主要是ι/2π = 0.4有理面处磁剪切的改变所导致的. 此外, 本文对电流幅度、宽度以及峰值位置等参数对磁岛的影响给予了深入探讨.Magnetic island produced in toroidal magnetic confinement plasma has a three-dimensional helical structure because of the rotational transform, especially the equilibrium magnetic surface of the stellarator is three-dimensional helical structure. Thus, the formation and instability of the magnetic island of the Stellarator is a typical issue of the three-dimensional physics and is also one of the key topics of the physics research of the Stellarator. Magnetic islands and related tearing mode physics are major issues in stellarator. The non-inductively current drive, i.e. electron cyclotron current drive (ECCD) can be used as one of the approaches to adjusting the rotational transform, and hence, affecting the generation of magnetic islands. In this study, we use an additional toroidal magnetic field to generate m/n = 5/2 magnetic islands in the low-β operation on the Chinese First Quasi-axisymmetric Stellarator (CFQS) so that the influence of the bootstrap current is negligible. Then, we investigate the suppression mechanism of magnetic islands in low-β plasma by using the HINT code. It is found that in the case of the constant current, when the current direction is positive, with the increase of current, the width of island increases. When the direction of current is reversed, the island is suppressed when the current is larger than 6 kA. The main reason is that the rotational transform is away from ι/2π = 0.4 rational surface and the m/n=5/2 magnetic island does not meet the resonance conditions. In the case of local current profile, the magnetic island width decreases as a result of the enhanced magnetic shear at ι/2π = 0.4 rational surface. Moreover, effects of the direction and the amplitude of the current on the suppression of magnetic islands are also discussed in more detail.
[1] ITER Physics Expert Group on Disruptions, Plasma Control, MHD and ITER Physics Basis Editors 1999 Nucl. Fusion 39 2251
 Google Scholar
Google Scholar
[2] Boozer A H 2012 Phys. Plasmas 19 058101
 Google Scholar
Google Scholar
[3] Hirsch M, Baldzuhn J, Beidler C, Brakel R, Burthenn R, Dinklage A, Ehmler H, Endler M, Erckmann V, Feng Y 2008 Plasma Phys. Control. Fusion 50 053001
 Google Scholar
Google Scholar
[4] Yamada H, Kawahata K, Mutoh T, et al. 2010 Fusion Sci. Technol. 58 12
 Google Scholar
Google Scholar
[5] Garabedian P R 1996 Phys. Plasmas 3 2483-2485.
 Google Scholar
Google Scholar
[6] Xu Y 2016 Matter and Radiation at Extremes 1 192
 Google Scholar
Google Scholar
[7] Nemov V V, Isobe M, Kernbichler W, et al. 2003 Plasma Phys. Controlled Fusion 45 1829
 Google Scholar
Google Scholar
[8] Okamura S, Murakmi S, Shimizu A, et al. 2000 J. Plasma Fusion Res. SERIES 3 73
[9] Okamura S, Matsuoka K, Nishimura S, et al. 2001 Nucl. Fusion 41 1865
 Google Scholar
Google Scholar
[10] Matsuoka K, Okamura S, Nishimura S, et al. 2004 Fusion Sci. Technol. 46 378
 Google Scholar
Google Scholar
[11] Okamura S, Matsuoka K, Nishimura S, et al. 2004 Nucl. Fusion 44 575
 Google Scholar
Google Scholar
[12] Reiman A, Ku L, Monticello D, et al. 2001 Phys. Plasmas 8 2083
 Google Scholar
Google Scholar
[13] Reiman A, Fu G, Hirshman S, et al. 1999 Plasma Phys. Controlled Fusion 41 B273
 Google Scholar
Google Scholar
[14] Neilson G H, Reiman A H, Zarnstorff M C, et al. 2000 Phys. Plasmas 7 1911
 Google Scholar
Google Scholar
[15] Zarnstorff M C, Berry L A, Brooks A, et al. 2001 Plasma Phys. Controlled Fusion 43 A237
 Google Scholar
Google Scholar
[16] Xu Y, Shimizu A, Liu B, et al. 2018 27th IAEA Fusion Energy Conference Gandhinagar, India, October 22–27, 2018, EX/P5-23
[17] 黄捷, 李沫杉, 覃程, 王先驱 2022 71 185202
 Google Scholar
Google Scholar
Huang J, Li M S, Qin C, Wang X Q 2022 Acta Phys. Sin 71 185202
 Google Scholar
Google Scholar
[18] Su C Y, Chen S Y, Liu H F, et al. 2020 AIP Adv. 10 015004
 Google Scholar
Google Scholar
[19] Harafuji K, Hayashi T, Sato T 1989 J. Comput. Phys. 81 169
 Google Scholar
Google Scholar
[20] Hirshman S P, Whitson J C. 1983 Phys. Fluids 26 3553
 Google Scholar
Google Scholar
[21] Suzuki Y 2017 Plasma Phys. Control. Fusion 59 054008
 Google Scholar
Google Scholar
[22] Suzuki Y 2020 Plasma Phys. Control. Fusion 62 104001
 Google Scholar
Google Scholar
[23] Suzuki Y, Nakajima N, Watanabe K, et al. 2006 Nucl. Fusion 46 L19
 Google Scholar
Google Scholar
[24] Liu H F, Shimizu A, Isobe M, et al. 2018 Plasma Fusion Res. 13 3405067
 Google Scholar
Google Scholar
[25] Liu H F, Shimizu A, Xu Y, et al. 2021 Nucl. Fusion 61 016014
 Google Scholar
Google Scholar
[26] Shimizu A, Liu H F, Isobe M, et al. 2018 Plasma Fusion Res. 13 3403123
 Google Scholar
Google Scholar
[27] Wang X Q, Xu Y, Shimizu A, et al. 2021 Nucl. Fusion 61 036021
 Google Scholar
Google Scholar
[28] Wesson J, Campbell D J, Connor J W, et al. 2004 Tokamaks (3rd Ed.) (New York: Oxford University Press) pp358–359
[29] Isayama A 2006 Plasma Sci. Technol. 8 36
 Google Scholar
Google Scholar
-
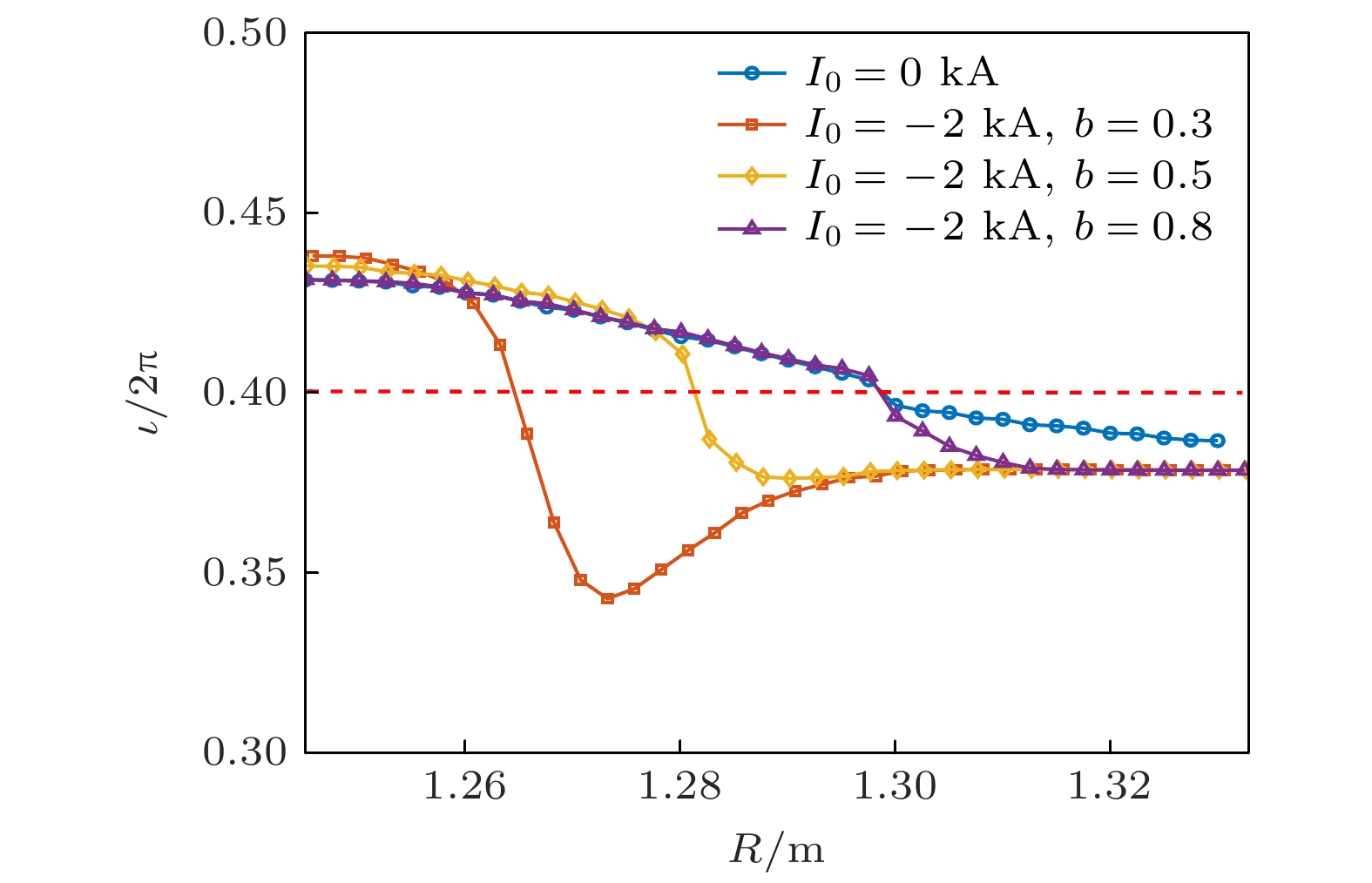
图 1 (a)
$\left\langle \beta \right\rangle = 0.5{\text{%}} $ 时旋转变换以及压强的径向分布; (b)$\left\langle \beta \right\rangle = 0.5{\text{%}} $ 、环向角$\phi = {0^ \circ }$ 时所对应的初始庞加莱图. 黑色点表示$p/{p_0} < 1{\text{%}} $ 的区域, 蓝色点表示$1{\text{%}} \leqslant $ $ p/{p_0} \leqslant 10{\text{%}} $ 的区域, 红色点表示$p/{p_0} > 10{\text{%}} $ 的区域, 绿色线为真空室Fig. 1. (a) Comparison of the radial dependence of the rotational transform and pressure,
$\iota /2\pi $ with$\left\langle \beta \right\rangle = 0.5{\text{%}} $ , between the HINT and VMEC codes; (b) the Poincaré plots of initial magnetic surfaces with$\left\langle \beta \right\rangle = 0.5{\text{%}} $ at toroidal angle$\phi = {0^ \circ }$ , where the black, blue and red colors mark the regions of$p/{p_0} < 1{\text{%}} $ ,$1{\text{%}} \leqslant p/{p_0} \leqslant 10{\text{%}} $ , and$p/{p_0} > $ $ 10{\text{%}} $ , respectively. The green line denotes the boundary of the vacuum vessel.图 4 (a)—(c)
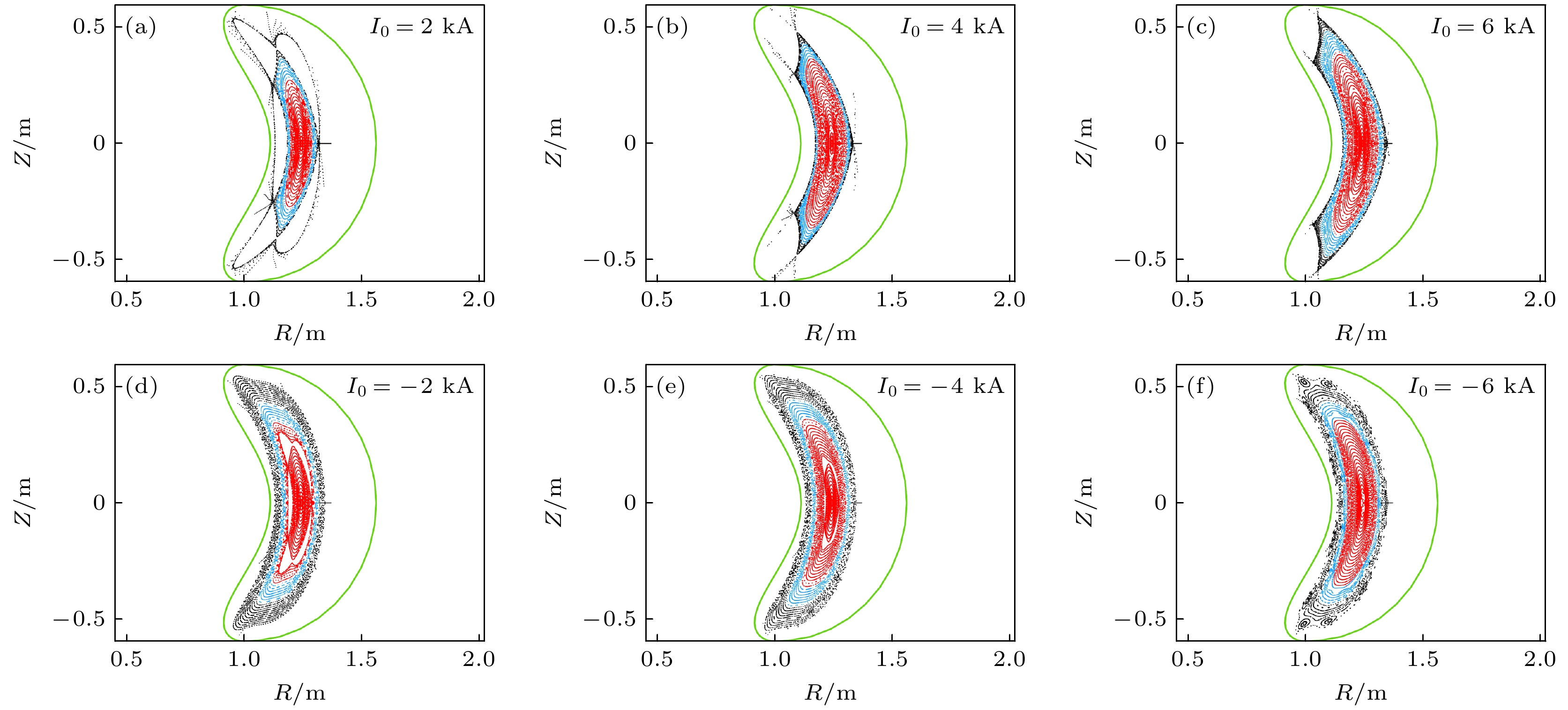
$ {I}_{0}=2, \text{ }4, \text{ }6\text{ kA} $ 时庞加莱磁面; (d)—(f) 为$ {I}_{0}=-2, \text{ }-4, \text{ }-6\text{ kA} $ 时庞加莱磁面Fig. 4. (a)–(c) Poincaré plots of magnetic surfaces with
$ {I}_{0}=2, \text{ }4, \text{ }6\text{ kA} $ ; (d)–(f) the Poincaré plots of magnetic surfaces with$ {I}_{0}=-2, \text{ }-4, \text{ }-6\text{ kA} $ . -
[1] ITER Physics Expert Group on Disruptions, Plasma Control, MHD and ITER Physics Basis Editors 1999 Nucl. Fusion 39 2251
 Google Scholar
Google Scholar
[2] Boozer A H 2012 Phys. Plasmas 19 058101
 Google Scholar
Google Scholar
[3] Hirsch M, Baldzuhn J, Beidler C, Brakel R, Burthenn R, Dinklage A, Ehmler H, Endler M, Erckmann V, Feng Y 2008 Plasma Phys. Control. Fusion 50 053001
 Google Scholar
Google Scholar
[4] Yamada H, Kawahata K, Mutoh T, et al. 2010 Fusion Sci. Technol. 58 12
 Google Scholar
Google Scholar
[5] Garabedian P R 1996 Phys. Plasmas 3 2483-2485.
 Google Scholar
Google Scholar
[6] Xu Y 2016 Matter and Radiation at Extremes 1 192
 Google Scholar
Google Scholar
[7] Nemov V V, Isobe M, Kernbichler W, et al. 2003 Plasma Phys. Controlled Fusion 45 1829
 Google Scholar
Google Scholar
[8] Okamura S, Murakmi S, Shimizu A, et al. 2000 J. Plasma Fusion Res. SERIES 3 73
[9] Okamura S, Matsuoka K, Nishimura S, et al. 2001 Nucl. Fusion 41 1865
 Google Scholar
Google Scholar
[10] Matsuoka K, Okamura S, Nishimura S, et al. 2004 Fusion Sci. Technol. 46 378
 Google Scholar
Google Scholar
[11] Okamura S, Matsuoka K, Nishimura S, et al. 2004 Nucl. Fusion 44 575
 Google Scholar
Google Scholar
[12] Reiman A, Ku L, Monticello D, et al. 2001 Phys. Plasmas 8 2083
 Google Scholar
Google Scholar
[13] Reiman A, Fu G, Hirshman S, et al. 1999 Plasma Phys. Controlled Fusion 41 B273
 Google Scholar
Google Scholar
[14] Neilson G H, Reiman A H, Zarnstorff M C, et al. 2000 Phys. Plasmas 7 1911
 Google Scholar
Google Scholar
[15] Zarnstorff M C, Berry L A, Brooks A, et al. 2001 Plasma Phys. Controlled Fusion 43 A237
 Google Scholar
Google Scholar
[16] Xu Y, Shimizu A, Liu B, et al. 2018 27th IAEA Fusion Energy Conference Gandhinagar, India, October 22–27, 2018, EX/P5-23
[17] 黄捷, 李沫杉, 覃程, 王先驱 2022 71 185202
 Google Scholar
Google Scholar
Huang J, Li M S, Qin C, Wang X Q 2022 Acta Phys. Sin 71 185202
 Google Scholar
Google Scholar
[18] Su C Y, Chen S Y, Liu H F, et al. 2020 AIP Adv. 10 015004
 Google Scholar
Google Scholar
[19] Harafuji K, Hayashi T, Sato T 1989 J. Comput. Phys. 81 169
 Google Scholar
Google Scholar
[20] Hirshman S P, Whitson J C. 1983 Phys. Fluids 26 3553
 Google Scholar
Google Scholar
[21] Suzuki Y 2017 Plasma Phys. Control. Fusion 59 054008
 Google Scholar
Google Scholar
[22] Suzuki Y 2020 Plasma Phys. Control. Fusion 62 104001
 Google Scholar
Google Scholar
[23] Suzuki Y, Nakajima N, Watanabe K, et al. 2006 Nucl. Fusion 46 L19
 Google Scholar
Google Scholar
[24] Liu H F, Shimizu A, Isobe M, et al. 2018 Plasma Fusion Res. 13 3405067
 Google Scholar
Google Scholar
[25] Liu H F, Shimizu A, Xu Y, et al. 2021 Nucl. Fusion 61 016014
 Google Scholar
Google Scholar
[26] Shimizu A, Liu H F, Isobe M, et al. 2018 Plasma Fusion Res. 13 3403123
 Google Scholar
Google Scholar
[27] Wang X Q, Xu Y, Shimizu A, et al. 2021 Nucl. Fusion 61 036021
 Google Scholar
Google Scholar
[28] Wesson J, Campbell D J, Connor J W, et al. 2004 Tokamaks (3rd Ed.) (New York: Oxford University Press) pp358–359
[29] Isayama A 2006 Plasma Sci. Technol. 8 36
 Google Scholar
Google Scholar
计量
- 文章访问数: 5945
- PDF下载量: 178
- 被引次数: 0































 下载:
下载: