-
交叉扩散是影响图灵斑图形成和转变的重要因素之一. 本文在反应扩散布鲁塞尔模型中引入交叉扩散项, 首先对其进行线性分析和弱非线性分析, 然后数值研究了交叉扩散的方向性以及浓度依赖性在图灵斑图转变过程中的作用. 在单向交叉扩散情况下, 交叉扩散的方向直接决定了斑图转变的次序. 阻滞子向活化子的交叉扩散会导致系统逐渐远离初级分岔点, 从而引发图灵斑图的正向转变; 与之相反, 活化子向阻滞子的交叉扩散会导致系统逐渐靠近初级分岔点, 从而引发图灵斑图的反向转变. 对称双向交叉扩散下, 阻滞子向活化子的交叉扩散效应要强于活化子向阻滞子的交叉扩散. 交叉扩散系数除了与自身浓度相关外, 还与其他物质浓度相关. 研究发现浓度依赖交叉扩散也会影响图灵斑图的转变方向. 当扩散系数
$ {D_{uv}} $ 线性依赖阻滞子浓度$ v $ 变化时, 随着浓度线性调节参数$ \beta $ 的增大, 引发图灵斑图正向转变; 相反, 当扩散系数$ {D_{vu}} $ 线性依赖活化子浓度$ u $ 变化时, 引发图灵斑图的反向转变.Cross-diffusion is one of the most important factors affecting the formation and transition of Turing patterns in reaction diffusion systems. In this paper, cross-diffusion is introduced into a reaction diffusion Brusselator model to investigate the effects of the directivity and density-dependence of cross-diffusion on Turing pattern transition. Turing space is obtained by the standard linear stability analysis, and the amplitude equations are derived based on weakly nonlinear method, by which Turing pattern selection can be determined theoretically. It is found that the degree of deviation from the primary Turing bifurcation point plays an important role in determining the process of pattern selection in the Turing region. As the deviation from onset is increased, the system exhibits a series of pattern transitions from homogenous state to honeycomb hexagonal pattern, to stripe pattern, and then to hexagonal spot pattern. In the case of one-way cross-diffusion, the direction of cross-diffusion determines the order of Turing pattern transition. The cross-diffusion from the inhibitor to the activator enhances the Turing mode and drives the system far away from the primary bifurcation point, resulting in the forward order of Turing pattern transition. On the contrary, the cross-diffusion from the activator to the inhibitor suppresses the Turing mode and forces the pattern transition in a reverse order. In the case of two-way cross-diffusion, the cross-diffusion effect from inhibitors to activators is stronger than that from activators to inhibitors with the same diffusion coefficient. Essentially, the cross-diffusion coefficient is dependent on not only the local concentration of species itself, but also the concentrations of other species due to their interaction. It is found that concentration dependent cross diffusion also affects the transformation direction of Turing pattern. When the diffusion coefficient$ {D_{uv}} $ is linearly dependent on the concentration of retarders, the positive transformation of the Turing pattern is induced with the increase of the concentration linear adjustment parameter$ \beta $ . On the contrary, when the diffusion coefficient$ {D_{vu}} $ is linearly dependent on the concentration of active particles, the reverse transformation of the Turing pattern is induced. The numerical simulation results are consistent with the theoretical analysis.-
Keywords:
- turing mechanism /
- pattern transition /
- cross-diffusion /
- directivity /
- density-dependent
[1] Gao S P, Chang L L, Perc M, Wang Z 2023 Phys. Rev. E 107 014216
Google Scholar
[2] Fuseya Y, Katsuno H, Behnia K, Kapitulnik A 2021 Nat. Phys. 17 1031
Google Scholar
[3] Halatek J, Frey E 2018 Nat. Phys. 14 507
Google Scholar
[4] Wang X L, Wang W D, Zhang G H 2017 Commun. Nonlinear Sci. Numer. Simulat. 42 571
Google Scholar
[5] Turing A M 1952 Philos. Trans. R. Soc. London Ser. B 237 37
Google Scholar
[6] Ouyang Q, Swinney H L 1991 Nature 352 610
Google Scholar
[7] Callahan T K, Knobloch E 1999 Physica D 132 339
Google Scholar
[8] Haas P A, Goldstein R E 2021 Phys. Rev. Lett. 126 238101
Google Scholar
[9] Landge A N, Jordan B M, Diego X, Muller P 2020 Dev. Biol. 460 2
Google Scholar
[10] Kumar N, Horsthemke W 2011 Phys. Rev. E 83 036105
Google Scholar
[11] Yang R 2022 Nonlinear Dyn. 110 1753
Google Scholar
[12] Tang X S, Song Y L, Zhang T H 2016 Nonlinear Dyn. 86 73
Google Scholar
[13] Vanag V K, Epstein I R 2009 Int. J. Dev. Biol. 53 673
Google Scholar
[14] Cui R F, Chen Q H, Chen J X 2020 Nanoscale 12 12275
Google Scholar
[15] Chen J X, Chen Y G, Kapral R 2018 Adv. Sci. 5 1800028
Google Scholar
[16] Kerner E H 1957 Bull. Math. Biol. 19 121
Google Scholar
[17] Souna F, Djilali S, Lakmeche A 2021 Eur. Phys. J. Plus 136 474
Google Scholar
[18] Guin L N 2015 Math. Comput. Simulat. 109 174
Google Scholar
[19] Gambino G, Lombardo M C, Sammartino M 2013 Nonlinear Anal. Real World Appl. 14 1755
Google Scholar
[20] Liu B, Wu R C, Chen L P 2018 Math. Biosci. 298 71
Google Scholar
[21] Ma T T, Meng X Z 2022 Math. Biosci. Eng. 19 6040
Google Scholar
[22] Xie Z F 2012 J. Math. Anal. Appl. 388 539
Google Scholar
[23] Chung J M, Peacock-López E 2007 Phys. Lett. A 371 41
Google Scholar
[24] Zhu L H, He L 2022 Nonlinear Dyn. 110 1935
Google Scholar
[25] Han R J, Dai B X 2019 Nonlinear Anal. Real World Appl. 45 822
Google Scholar
[26] Chen T R, Sun Z Y, Wu B Y 2017 Appl. Math. Model. 47 745
Google Scholar
[27] Li H L, Zhang L, Teng Z D, Jiang Y L 2015 J. Appl. Math. Comput. 53 223
Google Scholar
[28] Berenstein I, Beta C 2013 Chaos 23 033119
Google Scholar
[29] Wang P F, Zhao M, Yu H G, Dai C J, Wang N, Wang B B 2016 Discrete Dyn. Nat. Soc. 2016 4893451
Google Scholar
[30] Roussel C J, Roussel M R 2004 Prog. Biophys. Mol. Biol. 86 113
Google Scholar
[31] Ling Z, Zhang L, Lin Z G 2014 Appl. Math. Model. 38 5022
Google Scholar
[32] He Y F, Ai B Q, Dai C X, Song C, Wang R Q, Sun W T, Liu F C, Feng Y 2020 Phys. Rev. Lett. 124 75001
Google Scholar
[33] Zemskov E P, Kassner K, Hauser M J B, Horsthemke W 2013 Phys. Rev. E 87 032906
Google Scholar
[34] Li W S, Hu W Y, Pang Y C, Liu T R, Zhong W R, Shao Y Z 2012 Phys. Rev. E 85 066132
Google Scholar
[35] 胡文勇, 邵元智 2014 63 238202
Google Scholar
Hu W Y, Shao Y Z 2014 Acta Phys. Sin. 63 238202
Google Scholar
[36] Chen W Q, Zhang H, Ying H P, Li B W, Chen J X 2007 J. Chem. Phys. 127 154708
Google Scholar
[37] Picozzi A, Rica S 2008 EPL 84 34004
Google Scholar
[38] Roussel M R, Wang J C 2001 Phys. Rev. Lett. 87 188302
Google Scholar
[39] Gambino G, Lombardo M C, Sammartino M 2018 Phys. Rev. E 97 012220
Google Scholar
[40] Mukherjee N, Ghorai S, Banerjee M 2018 Ecol. Complex. 36 276
Google Scholar
[41] Liu C, Li L, Wang Z, Wang R W 2019 Appl. Math. Comput. 342 255
Google Scholar
[42] Peña B, Pérez-García C, Sanz-Anchelergues A, Miguez D G, Munuzuri A P 2003 Phys. Rev. E 68 056206
Google Scholar
[43] Yang R 2022 Chaos Solitons Fractals 164 112695
Google Scholar
[44] 欧阳颀 2010 非线性科学与斑图动力学导论(北京: 北京大学出版社) 第144—160页
Ouyang Q 2010 Nonlinear Science and the Pattern Dynamics Introduction (Beijing: Peking University Press) pp144–160
[45] Verdasca J, de Wit A, Dewel G, Borckmans P 1992 Phys. Lett. A 168 194
Google Scholar
[46] Song D X, Li C, Song Y L 2020 Nonlinear Anal. Real World Appl. 54 103106
Google Scholar
[47] 刘若琪, 贾萌萌, 范伟丽, 贺亚峰, 刘富成 2022 71 248201
Google Scholar
Liu R Q, Jia M M, Fan W L, He Y F, Liu F C 2022 Acta Phys. Sin. 71 248201
Google Scholar
-
图 1
$ a = 3 $ ,$ b = 9 $ ,$ {D_u} = 3 $ ,$ {D_v} = 10 $ 时, 交叉扩散存在下的图灵空间. 点线、粗实线、细实线和虚线分别对应(3a)式—(3d)式Fig. 1. Turing space in the present of cross diffusion for
$ a = 3 $ ,$ b = 9 $ ,$ {D_u} = 3 $ , and$ {D_v} = 10 $ . Thick solid line, dotted line, thin solid line, and dotted line correspond to Eqs. (3a)-(3d), respectively.
图 2 单向交叉扩散
$ {D_{uv}} $ 引发的图灵斑图转变 (a)色散曲线; (b)条纹斑图,$ {D_{uv}} = 0 $ ; (c)点状六边形与条纹混合斑图,$ {D_{uv}} = 2 $ ; (d)点状六边形斑图,$ {D_{uv}} = 4.5 $ Fig. 2. Turing pattern transition induced by one-way cross diffusion term
$ {D_{uv}} $ : (a) Dispersion curves; (b) stripe pattern,$ {D_{uv}} = 0 $ ; (c) mixed pattern with stripes and spots,$ {D_{uv}} = 2 $ ; (d) hexagonal spot pattern,$ {D_{uv}} = 4.5 $ .
图 3 单向交叉扩散
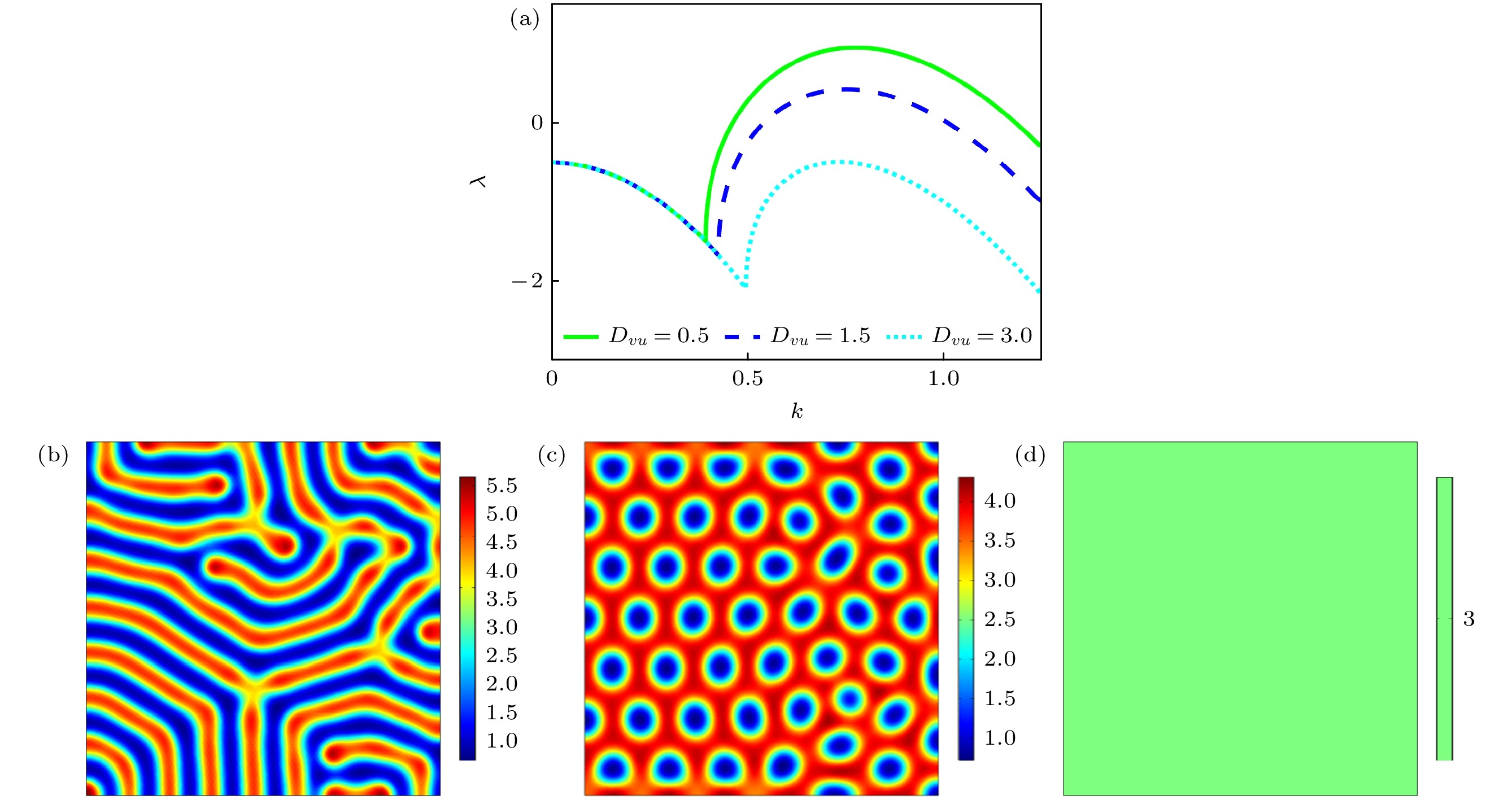
$ {D_{vu}} $ 引发的图灵斑图转变 (a)色散曲线; (b)条纹斑图,$ {D_{vu}} = 0.5 $ ; (c)蜂窝状六边形斑图,$ {D_{vu}} = 1.5 $ ; (d)均匀态,$ {D_{vu}} = 3 $ Fig. 3. Turing pattern transition induced by one-way cross diffusion term
$ {D_{vu}} $ : (a) Dispersion curves; (b) stripe pattern,$ {D_{vu}} = 0.5 $ ; (c) honeycomb hexagonal pattern,$ {D_{vu}} = 1.5 $ ; (d) uniform state,$ {D_{vu}} = 3 $ .
图 4 对称双向交叉扩散作用下图灵斑图的转变过程 (a)色散曲线; (b)条纹斑图,
$ {D_{uv}} = {D_{vu}} = 1 $ ; (c)蜂窝状六边形与条状混合斑图,$ {D_{uv}} = {D_{vu}} = 3 $ ; (d)多模混合斑图,$ {D_{uv}} = {D_{vu}} = 5 $ Fig. 4. Turing pattern transition induced by symmetrical two-way cross-diffusion: (a) Dispersion curves; (b) stripe pattern,
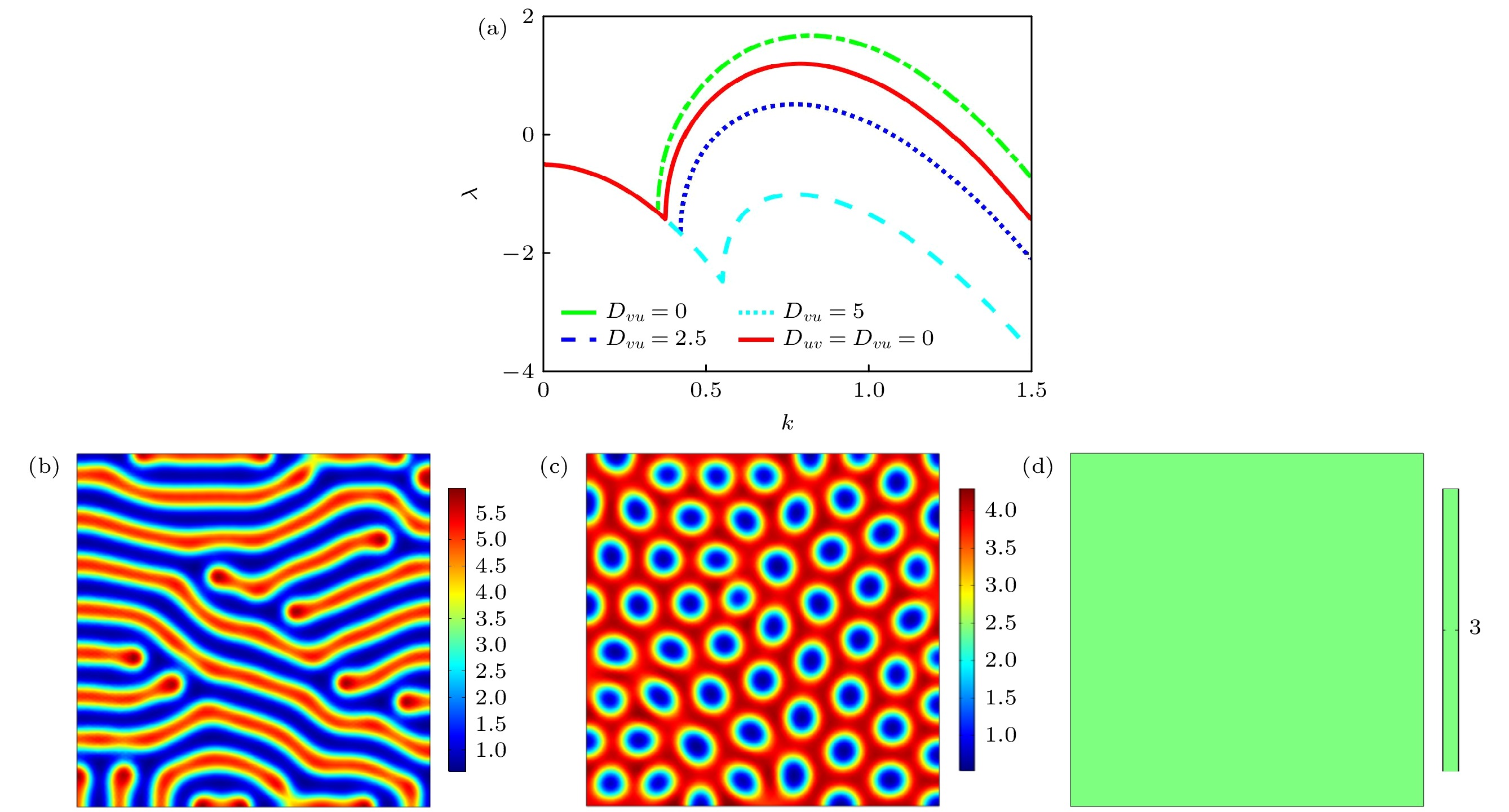
$ {D_{uv}} = {D_{vu}} = 1 $ ; (c) mixed pattern with honeycomb hexagons and stripes,$ {D_{uv}} = {D_{vu}} = 3 $ ; (d) multimode mixed pattern,$ {D_{uv}} = {D_{vu}} = 5 $ .
图 5 非对称交叉扩散项下图灵斑图的转变过程,
$ {D_{uv}} = 1 $ (a)色散曲线; (b)条纹斑图,$ {D_{vu}} = 0 $ ; (c)蜂窝状六边形斑图,$ {D_{vu}} = 2.5 $ ; (d)均匀态,$ {D_{vu}} = 5 $ Fig. 5. Turing pattern transition induced by asymmetrical two-way cross-diffusion at
$ {D_{uv}} = 1 $ : (a) Dispersion curves; (b) stripe pattern,$ {D_{vu}} = 0 $ ; (c) honeycomb hexagonal pattern,$ {D_{vu}} = 2.5 $ ; (d) uniform state,$ {D_{vu}} = 5 $ .
图 6 浓度依赖交叉扩散
$ {D_{uv}} = {D_0}(1 + \beta v) $ 引起图灵斑图的转变,$ {D_0} = 2 $ ,$ {D_{vu}} = 2 $ (a) 均匀态,$ \beta = - 0.6 $ ; (b) 蜂窝六边形斑图,$ \beta = - 0.4 $ ; (c) 蜂窝六边形与条纹混合斑图,$ \beta = - 0.2 $ ; (d) 条纹斑图,$ \beta = 0 $ ; (e) 条纹与点状混合斑图,$ \beta = 0.8 $ ; (f) 点状六边形斑图,$ \beta = 1.5 $ Fig. 6. Turing pattern transition induced by cross-diffusion coefficient with concentration-dependence (
$ {D_{uv}} = {D_0}(1 + \beta v) $ ),$ {D_0} = 2 $ ,$ {D_{vu}} = 2 $ : (a) Uniform state,$ \beta = - 0.6 $ ; (b) honeycomb hexagonal pattern,$ \beta = - 0.4 $ ; (c) mixed pattern with honeycomb hexagons and stripes,$ \beta = - 0.2 $ ; (d) stripe pattern,$ \beta = 0 $ ; (e) mixed pattern with stripes and spots,$ \beta = 0.8 $ ; (f) hexagonal spot pattern,$ \beta = 1.5 $ .
图 7 浓度依赖交叉扩散
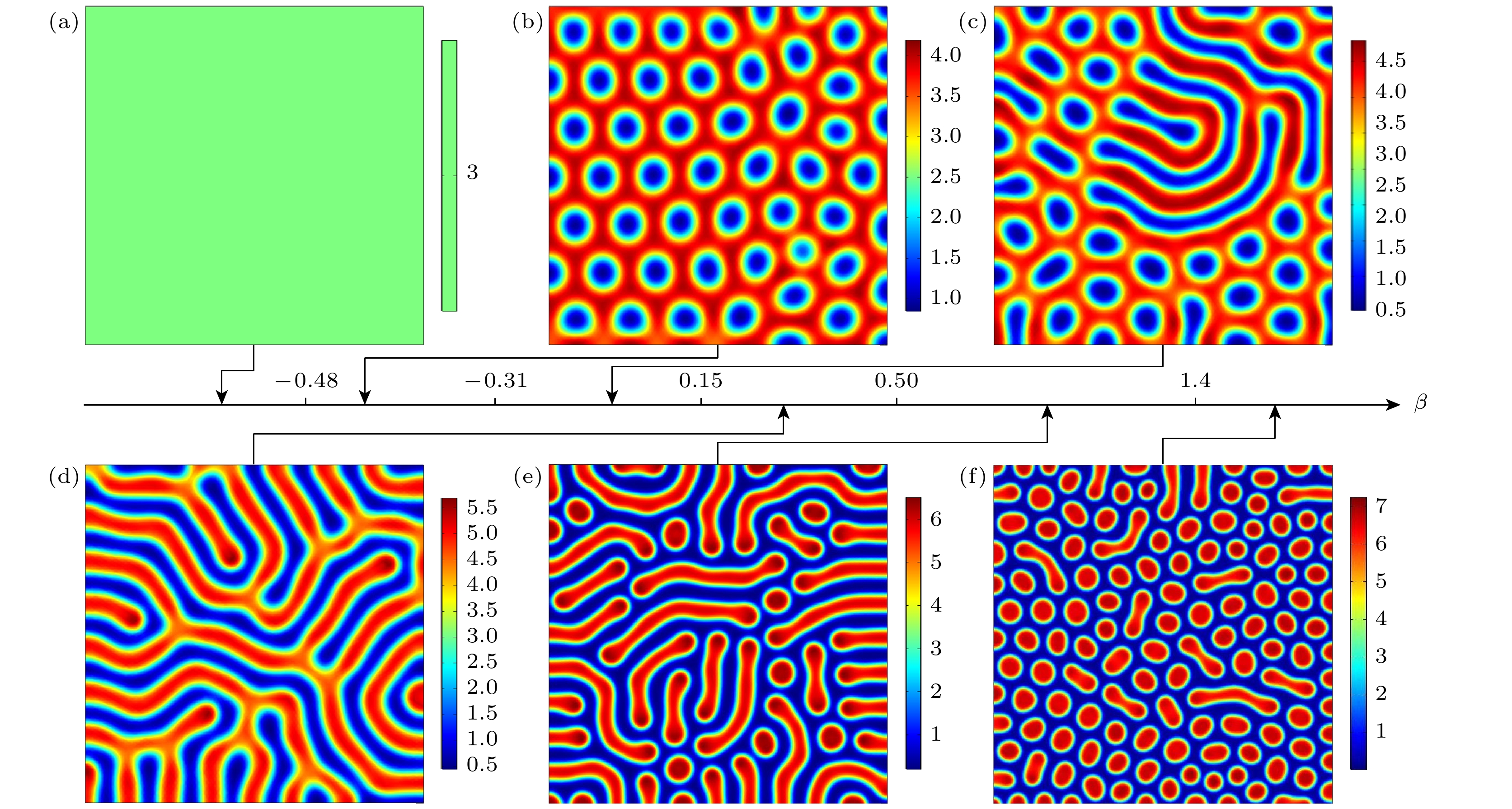
$ {D_{vu}} = {D_0}(1 + \beta u) $ 引起图灵斑图的转变,$ {D_0} = 2 $ ,$ {D_{uv}} = 2 $ (a) 点状六边形斑图,$ \beta = - 0.30 $ ; (b) 条纹与点状六边形混合斑图,$ \beta = - 0.22 $ ; (c) 条纹斑图,$ \beta = 0 $ ; (d) 蜂窝状六边形与条纹混合斑图,$ \beta = 0.08 $ ; (e) 蜂窝状六边形斑图,$ \beta = 0.20 $ ; (f) 均匀态,$ \beta = 0.80 $ Fig. 7. Turing pattern transition induced by cross-diffusion coefficient with concentration-dependence (
$ {D_{vu}} = {D_0}(1 + \beta u) $ ),$ {D_0} = 2 $ ,$ {D_{uv}} = 2 $ : (a) Hexagonal spot pattern,$ \beta = - 0.30 $ ; (b) mixed pattern with stripes and spots,$ \beta = - 0.22 $ ; (c) stripe pattern,$ \beta = 0 $ ; (d) mixed pattern with honeycomb hexagons and stripes,$ \beta = 0.08 $ ; (e) honeycomb hexagonal pattern,$ \beta = 0.20 $ ; (f) uniform state,$ \beta = 0.80 $ . -
[1] Gao S P, Chang L L, Perc M, Wang Z 2023 Phys. Rev. E 107 014216
Google Scholar
[2] Fuseya Y, Katsuno H, Behnia K, Kapitulnik A 2021 Nat. Phys. 17 1031
Google Scholar
[3] Halatek J, Frey E 2018 Nat. Phys. 14 507
Google Scholar
[4] Wang X L, Wang W D, Zhang G H 2017 Commun. Nonlinear Sci. Numer. Simulat. 42 571
Google Scholar
[5] Turing A M 1952 Philos. Trans. R. Soc. London Ser. B 237 37
Google Scholar
[6] Ouyang Q, Swinney H L 1991 Nature 352 610
Google Scholar
[7] Callahan T K, Knobloch E 1999 Physica D 132 339
Google Scholar
[8] Haas P A, Goldstein R E 2021 Phys. Rev. Lett. 126 238101
Google Scholar
[9] Landge A N, Jordan B M, Diego X, Muller P 2020 Dev. Biol. 460 2
Google Scholar
[10] Kumar N, Horsthemke W 2011 Phys. Rev. E 83 036105
Google Scholar
[11] Yang R 2022 Nonlinear Dyn. 110 1753
Google Scholar
[12] Tang X S, Song Y L, Zhang T H 2016 Nonlinear Dyn. 86 73
Google Scholar
[13] Vanag V K, Epstein I R 2009 Int. J. Dev. Biol. 53 673
Google Scholar
[14] Cui R F, Chen Q H, Chen J X 2020 Nanoscale 12 12275
Google Scholar
[15] Chen J X, Chen Y G, Kapral R 2018 Adv. Sci. 5 1800028
Google Scholar
[16] Kerner E H 1957 Bull. Math. Biol. 19 121
Google Scholar
[17] Souna F, Djilali S, Lakmeche A 2021 Eur. Phys. J. Plus 136 474
Google Scholar
[18] Guin L N 2015 Math. Comput. Simulat. 109 174
Google Scholar
[19] Gambino G, Lombardo M C, Sammartino M 2013 Nonlinear Anal. Real World Appl. 14 1755
Google Scholar
[20] Liu B, Wu R C, Chen L P 2018 Math. Biosci. 298 71
Google Scholar
[21] Ma T T, Meng X Z 2022 Math. Biosci. Eng. 19 6040
Google Scholar
[22] Xie Z F 2012 J. Math. Anal. Appl. 388 539
Google Scholar
[23] Chung J M, Peacock-López E 2007 Phys. Lett. A 371 41
Google Scholar
[24] Zhu L H, He L 2022 Nonlinear Dyn. 110 1935
Google Scholar
[25] Han R J, Dai B X 2019 Nonlinear Anal. Real World Appl. 45 822
Google Scholar
[26] Chen T R, Sun Z Y, Wu B Y 2017 Appl. Math. Model. 47 745
Google Scholar
[27] Li H L, Zhang L, Teng Z D, Jiang Y L 2015 J. Appl. Math. Comput. 53 223
Google Scholar
[28] Berenstein I, Beta C 2013 Chaos 23 033119
Google Scholar
[29] Wang P F, Zhao M, Yu H G, Dai C J, Wang N, Wang B B 2016 Discrete Dyn. Nat. Soc. 2016 4893451
Google Scholar
[30] Roussel C J, Roussel M R 2004 Prog. Biophys. Mol. Biol. 86 113
Google Scholar
[31] Ling Z, Zhang L, Lin Z G 2014 Appl. Math. Model. 38 5022
Google Scholar
[32] He Y F, Ai B Q, Dai C X, Song C, Wang R Q, Sun W T, Liu F C, Feng Y 2020 Phys. Rev. Lett. 124 75001
Google Scholar
[33] Zemskov E P, Kassner K, Hauser M J B, Horsthemke W 2013 Phys. Rev. E 87 032906
Google Scholar
[34] Li W S, Hu W Y, Pang Y C, Liu T R, Zhong W R, Shao Y Z 2012 Phys. Rev. E 85 066132
Google Scholar
[35] 胡文勇, 邵元智 2014 63 238202
Google Scholar
Hu W Y, Shao Y Z 2014 Acta Phys. Sin. 63 238202
Google Scholar
[36] Chen W Q, Zhang H, Ying H P, Li B W, Chen J X 2007 J. Chem. Phys. 127 154708
Google Scholar
[37] Picozzi A, Rica S 2008 EPL 84 34004
Google Scholar
[38] Roussel M R, Wang J C 2001 Phys. Rev. Lett. 87 188302
Google Scholar
[39] Gambino G, Lombardo M C, Sammartino M 2018 Phys. Rev. E 97 012220
Google Scholar
[40] Mukherjee N, Ghorai S, Banerjee M 2018 Ecol. Complex. 36 276
Google Scholar
[41] Liu C, Li L, Wang Z, Wang R W 2019 Appl. Math. Comput. 342 255
Google Scholar
[42] Peña B, Pérez-García C, Sanz-Anchelergues A, Miguez D G, Munuzuri A P 2003 Phys. Rev. E 68 056206
Google Scholar
[43] Yang R 2022 Chaos Solitons Fractals 164 112695
Google Scholar
[44] 欧阳颀 2010 非线性科学与斑图动力学导论(北京: 北京大学出版社) 第144—160页
Ouyang Q 2010 Nonlinear Science and the Pattern Dynamics Introduction (Beijing: Peking University Press) pp144–160
[45] Verdasca J, de Wit A, Dewel G, Borckmans P 1992 Phys. Lett. A 168 194
Google Scholar
[46] Song D X, Li C, Song Y L 2020 Nonlinear Anal. Real World Appl. 54 103106
Google Scholar
[47] 刘若琪, 贾萌萌, 范伟丽, 贺亚峰, 刘富成 2022 71 248201
Google Scholar
Liu R Q, Jia M M, Fan W L, He Y F, Liu F C 2022 Acta Phys. Sin. 71 248201
Google Scholar
下载:
计量
- 文章访问数: 3229
- PDF下载量: 133
- 被引次数: 0
